介绍

在深度学习领域，卷积神经网络（CNNs）已经成为一个基石，特别是在计算机视觉领域。CNN的一个关键元素是它们使用的滤波器或核，这些核使得网络能够自动地从输入数据如图像中学习空间特征的层次结构。本文深入探讨了滤波器在CNN中的角色、机制和含义，提供了洞见，说明它们是如何在图像识别、对象检测等任务中提高这些网络效果的。

CNN中的滤波器概念

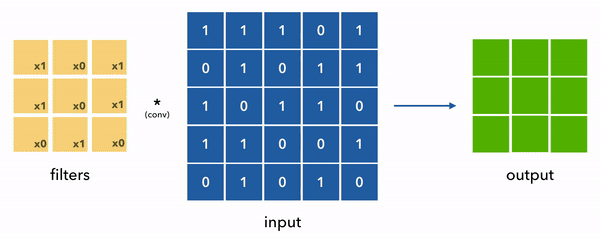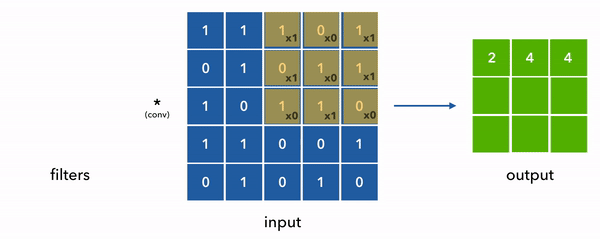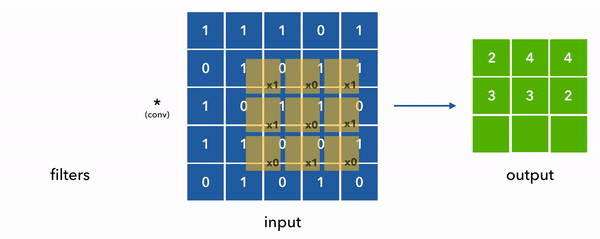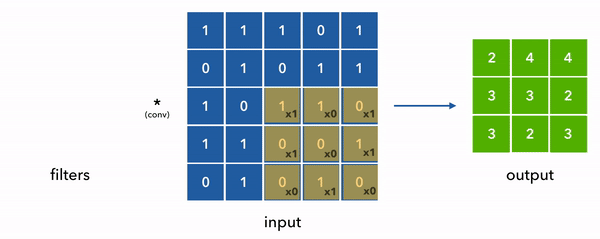
在其核心，CNN中的滤波器是用来检测图像中的特定特征（如边缘、纹理或模式）的小矩阵。这些滤波器通过称为卷积的过程应用于输入数据。这个过程的主要目的是特征提取，这对CNN理解和解释视觉数据至关重要。

滤波器的工作原理

1. 初始化和学习：CNN中的滤波器初始时是随机设置的，并在训练过程中进行精炼。随着网络接触到更多数据，它利用反向传播和梯度下降算法调整滤波器值，增强其提取相关特征的能力。
2. 卷积操作：在卷积中，滤波器在输入图像上滑动，在每个位置执行逐元素乘法，然后进行求和。这个操作生成一个特征图，突出了输入中的特定特征的存在。
3. 分层特征提取：CNN通常有多个卷积层。每一层提取越来越复杂的特征。初始层可能捕捉基本元素如边缘，而更深的层可以识别复杂的模式或对象。
4. 激活函数的非线性变换：卷积后，特征图通常会通过像ReLU这样的激活函数。这种非线性变换让CNN能学习复杂模式，做出更细致的预测。
5. 使用池化降低维数：在卷积之后，池化层减少表示的空间大小，减少计算负担，使得网络能够专注于最显著的特征。
6. 集成到深层网络中：最后，卷积和池化层的输出被输入到全连接层进行任务，如分类。这种层次结构让CNN能理解复杂和高维的数据。

在自动学习空间特征层级方面，CNN滤波器是基本的，这使得它们非常适用于任务，如图像识别、物体检测和计算机视觉中的许多其他应用。

影响与应用

滤波器的使用具有深远的影响。例如，在图像识别中，滤波器使CNN能以惊人的准确性识别和区分各种物体和模式。在医学成像中，它们有助于检测异常，如肿瘤。滤波器在视频分析和自动驾驶车辆导航中也是关键，其中实时特征提取至关重要。

挑战与未来方向

尽管它们非常有效，但CNN滤波器面临挑战，尤其是在向未见数据泛化和计算效率方面。未来的研究旨在开发更加适应性强的滤波器，能够以较低的计算需求处理多样化和动态的数据集。

代码

创建一个完整的Python示例，演示使用卷积神经网络(CNN)中的滤波器和绘图处理合成数据集，涉及多个步骤。我们将使用像TensorFlow和Matplotlib这样的库来实现这一目的。这个示例包括：

1. 生成一个合成数据集。
2. 定义一个简单的具有卷积层的CNN。
3. 在合成数据集上训练CNN。
4. 可视化滤波器和结果。

让我们从代码开始：

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
# Generate a synthetic dataset
def generate_synthetic_data(num_samples=5000, img_size=(28, 28)):
    # Simple synthetic images: horizontal and vertical lines
    data = np.zeros((num_samples, img_size[0], img_size[1], 1), dtype='float32')
    labels = np.zeros((num_samples,), dtype='int')
    for i in range(num_samples):
        if np.random.rand() > 0.5:
            # Vertical line
            x = np.random.randint(0, img_size[1])
            data[i, :, x, 0] = 1.
            labels[i] = 1
        else:
            # Horizontal line
            y = np.random.randint(0, img_size[0])
            data[i, y, :, 0] = 1.
            labels[i] = 0
    return data, labels
# Create the synthetic dataset
data, labels = generate_synthetic_data()
train_data, test_data = data[:4000], data[4000:]
train_labels, test_labels = labels[:4000], labels[4000:]
# Define a simple CNN
model = models.Sequential([
    layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)),
    layers.MaxPooling2D((2, 2)),
    layers.Flatten(),
    layers.Dense(64, activation='relu'),
    layers.Dense(2, activation='softmax')
])
# Compile the model
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
# Train the CNN on the synthetic dataset
history = model.fit(train_data, train_labels, epochs=10, 
                    validation_data=(test_data, test_labels))
# Plot training history
plt.plot(history.history['accuracy'], label='accuracy')
plt.plot(history.history['val_accuracy'], label='val_accuracy')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.ylim([0, 1])
plt.legend(loc='lower right')
plt.show()
# Function to visualize filters
def visualize_filters(model):
    for layer in model.layers:
        if 'conv' not in layer.name:
            continue
        filters, biases = layer.get_weights()
        f_min, f_max = filters.min(), filters.max()
        filters = (filters - f_min) / (f_max - f_min)
        
        # Plot first few filters
        n_filters, ix = 6, 1
        plt.figure(figsize=(20, 5))
        for i in range(n_filters):
            f = filters[:, :, 0, i]
            ax = plt.subplot(1, n_filters, ix)
            ax.set_xticks([])
            ax.set_yticks([])
            plt.imshow(f, cmap='gray')
            ix += 1
        plt.show()
# Visualize the filters of the first layer
visualize_filters(model)

• 合成数据生成：generate_synthetic_data 函数创建包含水平线或垂直线的简单图像。这是一个二分类问题。
• CNN 定义：使用 TensorFlow 的 Keras API 定义了一个简单的 CNN。它包括卷积层、池化层和全连接层。
• 训练：在人工合成数据集上对模型进行训练。
• 绘制训练历史：绘制训练和验证的准确率，以观察学习过程。
• 过滤器可视化：visualize_filters 函数提取并可视化来自卷积层的过滤器。

Epoch 1/10
125/125 [==============================] - 6s 29ms/step - loss: 0.0610 - accuracy: 0.9890 - val_loss: 5.9017e-04 - val_accuracy: 1.0000
Epoch 2/10
125/125 [==============================] - 3s 25ms/step - loss: 3.7370e-04 - accuracy: 1.0000 - val_loss: 2.1575e-04 - val_accuracy: 1.0000
Epoch 3/10
125/125 [==============================] - 3s 26ms/step - loss: 1.6139e-04 - accuracy: 1.0000 - val_loss: 1.1065e-04 - val_accuracy: 1.0000
Epoch 4/10
125/125 [==============================] - 4s 31ms/step - loss: 8.9679e-05 - accuracy: 1.0000 - val_loss: 6.6610e-05 - val_accuracy: 1.0000
Epoch 5/10
125/125 [==============================] - 3s 27ms/step - loss: 5.6774e-05 - accuracy: 1.0000 - val_loss: 4.4084e-05 - val_accuracy: 1.0000
Epoch 6/10
125/125 [==============================] - 3s 26ms/step - loss: 3.8548e-05 - accuracy: 1.0000 - val_loss: 3.0755e-05 - val_accuracy: 1.0000
Epoch 7/10
125/125 [==============================] - 3s 26ms/step - loss: 2.7756e-05 - accuracy: 1.0000 - val_loss: 2.2707e-05 - val_accuracy: 1.0000
Epoch 8/10
125/125 [==============================] - 4s 34ms/step - loss: 2.0939e-05 - accuracy: 1.0000 - val_loss: 1.7408e-05 - val_accuracy: 1.0000
Epoch 9/10
125/125 [==============================] - 3s 26ms/step - loss: 1.6325e-05 - accuracy: 1.0000 - val_loss: 1.3749e-05 - val_accuracy: 1.0000
Epoch 10/10
125/125 [==============================] - 3s 24ms/step - loss: 1.3055e-05 - accuracy: 1.0000 - val_loss: 1.1098e-05 - val_accuracy: 1.0000

你可以在安装了 TensorFlow 和 Matplotlib 的 Python 环境中运行这段代码。这将使你直接了解卷积神经网络(CNN)中的过滤器是如何在训练过程中操作和发展的。

总结

在深度学习领域，尤其是在处理和解释视觉数据时，卷积神经网络中的过滤器发挥了至关重要的作用。它们提取特征的能力、学习复杂模式以及适应各种输入，使它们成为现代人工智能应用中不可或缺的组件。随着研究的进展，我们可以期待过滤器的使用更加精细和高效，从而扩大 CNN 解决复杂实际问题能力的范围。