在本文中，我将尝试从头开始创建一个小规模的稳定扩散类模型。这里的小规模意味着我们将使用你可能听说过的小型数据集MNIST 。选择这个数据集的原因是训练过程不应该花费太多时间，让我们能够快速检查我们的结果是否变得更好。在整个博客中，你看到的所有代码都可以在我的 GitHub 存储库中找到。

先决条件

为了实现快速训练，使用GPU至关重要。确保你对面向对象编程（OOP）和神经网络（NN）有基本的理解。熟悉PyTorch在编码过程中也会有所帮助。如果没有GPU可用，你可以将代码中出现的设备值修改为‘cpu’。

Topic                 Video Link
OOP                   OOP Video
Neural Network        Neural Network Video
Pytorch               Pytorch Video
Linear Algebra        Linear Algebra Video

稳定扩散模型如何工作？

与许多其他图像生成模型不同，稳定扩散模型是一种扩散模型。简单来说，扩散模型使用模糊噪声对图像进行编码。然后使用一个噪声预测器以及一个逆向扩散过程来重建图像。

除了扩散模型的技术差异之外，稳定扩散的特别之处在于它不使用图片的像素空间。相反，它使用了简化的潜在空间。

这种选择是由于分辨率为512x512的彩色图像有巨大数量的潜在取值。相比之下，稳定扩散使用的压缩图像小了48倍，包含的取值更少。这种显著降低的处理需求使得在配备有8GB RAM的NVIDIA GPU的台式电脑上使用稳定扩散成为可能。小型潜在空间的有效性基于自然图像遵循模式而非随机性的观点。稳定扩散在解码器中使用变分自编码器（VAE）文件来捕捉精细细节，如眼睛。

Stable Diffusion V1的训练使用了三个由LAION从Common Crawl编译的数据集。这包括有着6分或更高美学评分的图片的LAION-Aesthetics v2.6数据集。

稳定扩散的架构

稳定扩散使用几个主要的架构组件，在这次探索中，我们将构建这些组件：

• 变分自编码器： 包含一个编码器和一个解码器。 编码器将一张 512x512 像素的图片压缩成一个较小的 64x64 模型，存储在潜在空间中。 解码器将潜在空间中的模型恢复为完整尺寸的 512x512 像素图片。
• 正向扩散： 逐步对图像添加高斯噪声，直到只剩下随机噪声。 用于训练时，但不用于其他任务，除了图像到图像的转换。
• 反向扩散： 迭代地撤销正向扩散。 在数十亿幅图像上进行训练，使用提示来创造独特的图像。
• 噪声预测器（U-Net）： 使用 U-Net 模型来对图像进行去噪。 U-Net 模型是卷积神经网络，稳定扩散使用了残差神经网络（ResNet）模型。
• 文本调节： 文本提示是常见的条件化形式。 CLIP 分词器分析文本提示中的每个词，并将数据嵌入到一个 768 值的向量中。 提示中最多可以使用 75 个标记。 文本提示由文本编码器传输到 U-Net 噪声预测器中，使用一个文本变换器。 将随机数生成器的种子设置为一个随机数，会在潜在空间中生成不同的图像。

这些组件协同工作，使稳定扩散能够以独特而可控的方式创建和操纵图像。

了解数据集

我们将使用 torchvision 模块中的 MNIST 数据集，它包含的是小型的 28x28 手写数字图像（0-9）。正如之前提到的，我们需要一个小型数据集以便训练不会耗时太长。让我们来看一下我们的数据集长什么样子。

# Import the required libraries
import torch
import torchvision
from torchvision import transforms
import matplotlib.pyplot as plt
# Define a transform to normalize the data
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])
# Download and load the training dataset
train_dataset = torchvision.datasets.MNIST(root='./data', train=True, transform=transform, download=True)
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=64, shuffle=True)
# Extract a batch of unique images
unique_images, unique_labels = next(iter(train_loader))
unique_images = unique_images.numpy()
# Display a grid of unique images
fig, axes = plt.subplots(4, 16, figsize=(16, 4), sharex=True, sharey=True)  # Create a 4x16 grid of subplots with a wider figure
for i in range(4):  # Loop over rows
    for j in range(16):  # Loop over columns
        index = i * 16 + j  # Calculate the index in the batch
        axes[i, j].imshow(unique_images[index].squeeze(), cmap='gray')  # Show the image using a grayscale colormap
        axes[i, j].axis('off')  # Turn off axis labels and ticks
plt.show()  # Display the plot

我们的数据集包含60,000张正方形图片，展示了从0到9不同的手绘数字。我们将要构建稳定扩散架构，并使用这些图片训练我们的模型。在训练过程中，我们将会尝试各种参数值。一旦模型训练完成，我们只需给它一个数字，比如5，它就会为我们生成一张手绘数字5的图像。

搭建舞台

在这个项目中，我们将使用一系列Python库，所以让我们先导入它们：

# Import the PyTorch library for tensor operations.
import torch
# Import the neural network module from PyTorch.
import torch.nn as nn
# Import functional operations from PyTorch.
import torch.nn.functional as F
# Import the 'numpy' library for numerical operations.
import numpy as np
# Import the 'functools' module for higher-order functions.
import functools
# Import the Adam optimizer from PyTorch.
from torch.optim import Adam
# Import the DataLoader class from PyTorch for handling datasets.
from torch.utils.data import DataLoader
# Import data transformation functions from torchvision.
import torchvision.transforms as transforms
# Import the MNIST dataset from torchvision.
from torchvision.datasets import MNIST
# Import 'tqdm' for creating progress bars during training.
import tqdm
# Import 'trange' and 'tqdm' specifically for notebook compatibility.
from tqdm.notebook import trange, tqdm
# Import the learning rate scheduler from PyTorch.
from torch.optim.lr_scheduler import MultiplicativeLR, LambdaLR
# Import the 'matplotlib.pyplot' library for plotting graphs.
import matplotlib.pyplot as plt
# Import the 'make_grid' function from torchvision.utils for visualizing image grids.
from torchvision.utils import make_grid
# Importing the `rearrange` function from the `einops` library
from einops import rearrange
# Importing the `math` module for mathematical operations
import math

请确保安装这些库以避免任何错误：

# Install the 'einops' library for easy manipulation of tensors
pip install einops
# Install the 'lpips' library for computing perceptual similarity between images
pip install lpips

在导入必要的库之后，让我们继续创建稳定扩散结构的第一个组件。

创建基础的正向扩散

让我们从正向扩散开始。基本上，扩散方程是：

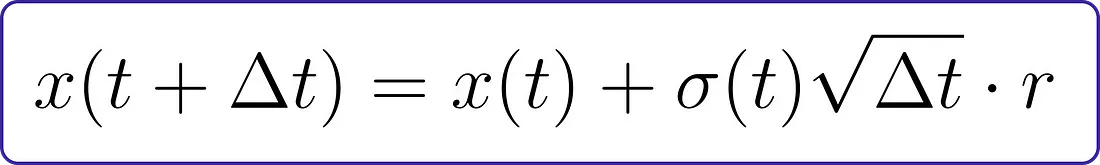
在这里，σ(t)>0是噪声强度，Δt是步长大小，而r∼N(0,1)是一个标准正态随机变量。简单地说，我们不断地向我们的样本中添加正态分布的噪声。通常，噪声强度σ(t)会随时间增长而选择增加（随着t变得更大）。

# Forward diffusion for N steps in 1D.
def forward_diffusion_1D(x0, noise_strength_fn, t0, nsteps, dt):
    """
    Parameters:
    - x0: Initial sample value (scalar)
    - noise_strength_fn: Function of time, outputs scalar noise strength
    - t0: Initial time
    - nsteps: Number of diffusion steps
    - dt: Time step size
    Returns:
    - x: Trajectory of sample values over time
    - t: Corresponding time points for the trajectory
    """
    # Initialize the trajectory array
    x = np.zeros(nsteps + 1)
    
    # Set the initial sample value
    x[0] = x0
    # Generate time points for the trajectory
    t = t0 + np.arange(nsteps + 1) * dt
    # Perform Euler-Maruyama time steps for diffusion simulation
    for i in range(nsteps):
        # Get the noise strength at the current time
        noise_strength = noise_strength_fn(t[i])
        # Generate a random normal variable
        random_normal = np.random.randn()
        # Update the trajectory using Euler-Maruyama method
        x[i + 1] = x[i] + random_normal * noise_strength
    # Return the trajectory and corresponding time points
    return x, t

将噪声强度函数设置为始终等于1。

# Example noise strength function: always equal to 1
def noise_strength_constant(t):
    """
    Example noise strength function that returns a constant value (1).
    Parameters:
    - t: Time parameter (unused in this example)
    Returns:
    - Constant noise strength (1)
    """
    return 1

既然我们已经定义了我们的正向扩散组件，让我们检查一下它是否在不同的试验中正常工作。

# Number of diffusion steps
nsteps = 100
# Initial time
t0 = 0
# Time step size
dt = 0.1
# Noise strength function
noise_strength_fn = noise_strength_constant
# Initial sample value
x0 = 0
# Number of tries for visualization
num_tries = 5
# Setting larger width and smaller height for the plot
plt.figure(figsize=(15, 5))
# Loop for multiple trials
for i in range(num_tries):
    # Simulate forward diffusion
    x, t = forward_diffusion_1D(x0, noise_strength_fn, t0, nsteps, dt)
    # Plot the trajectory
    plt.plot(t, x, label=f'Trial {i+1}')  # Adding a label for each trial
# Labeling the plot
plt.xlabel('Time', fontsize=20)
plt.ylabel('Sample Value ($x$)', fontsize=20)
# Title of the plot
plt.title('Forward Diffusion Visualization', fontsize=20)
# Adding a legend to identify each trial
plt.legend()
# Show the plot
plt.show()

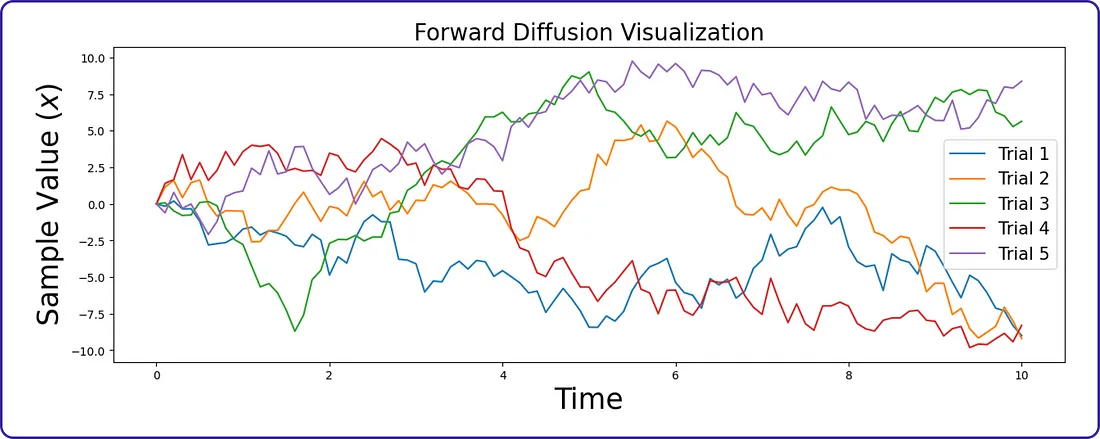
这个可视化展示了前向扩散过程，可以理解为慢慢地向起始样本中引入噪声。正如图表所显示的，随着扩散过程的进行，这导致生成了各种样本。

创建基础的逆向扩散

为了撤销这个扩散过程，我们使用了一个类似的更新规则：

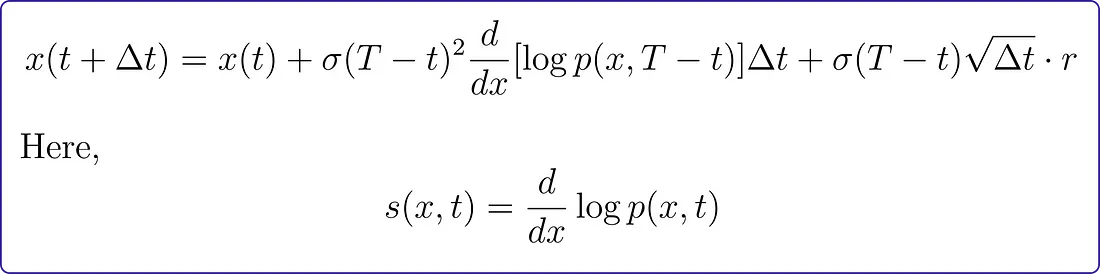
s(x,t) 被称为得分函数。知道这个函数使我们能够逆转前向扩散，并将噪声还原为我们的初始状态。

如果我们的起点始终是 x0​=0 的单一点，并且噪声强度是恒定的，那么得分函数恰好等于

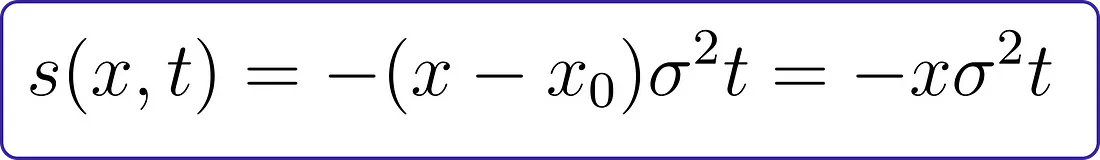
现在我们知道了数学方程式，让我们首先编写一维反向扩散函数的代码。

# Reverse diffusion for N steps in 1D.
def reverse_diffusion_1D(x0, noise_strength_fn, score_fn, T, nsteps, dt):
    """
    Parameters:
    - x0: Initial sample value (scalar)
    - noise_strength_fn: Function of time, outputs scalar noise strength
    - score_fn: Score function
    - T: Final time
    - nsteps: Number of diffusion steps
    - dt: Time step size
    Returns:
    - x: Trajectory of sample values over time
    - t: Corresponding time points for the trajectory
    """
    # Initialize the trajectory array
    x = np.zeros(nsteps + 1)
    
    # Set the initial sample value
    x[0] = x0
    # Generate time points for the trajectory
    t = np.arange(nsteps + 1) * dt
    # Perform Euler-Maruyama time steps for reverse diffusion simulation
    for i in range(nsteps):
        # Calculate noise strength at the current time
        noise_strength = noise_strength_fn(T - t[i])
        # Calculate the score using the score function
        score = score_fn(x[i], 0, noise_strength, T - t[i])
        # Generate a random normal variable
        random_normal = np.random.randn()
        # Update the trajectory using the reverse Euler-Maruyama method
        x[i + 1] = x[i] + score * noise_strength**2 * dt + noise_strength * random_normal * np.sqrt(dt)
    # Return the trajectory and corresponding time points
    return x, t

现在，我们将编写一个非常简单的分数函数，它的值总是等于1。

# Example score function: always equal to 1
def score_simple(x, x0, noise_strength, t):
    """
    Parameters:
    - x: Current sample value (scalar)
    - x0: Initial sample value (scalar)
    - noise_strength: Scalar noise strength at the current time
    - t: Current time
    Returns:
    - score: Score calculated based on the provided formula
    """
    # Calculate the score using the provided formula
    score = - (x - x0) / ((noise_strength**2) * t)
    # Return the calculated score
    return score

就像我们绘制我们的正向扩散函数来检查它是否正常工作一样，我们将对我们的逆向扩散函数做同样的事情。

# Number of reverse diffusion steps
nsteps = 100
# Initial time for reverse diffusion
t0 = 0
# Time step size for reverse diffusion
dt = 0.1
# Function defining constant noise strength for reverse diffusion
noise_strength_fn = noise_strength_constant
# Example score function for reverse diffusion
score_fn = score_simple
# Initial sample value for reverse diffusion
x0 = 0
# Final time for reverse diffusion
T = 11
# Number of tries for visualization
num_tries = 5
# Setting larger width and smaller height for the plot
plt.figure(figsize=(15, 5))
# Loop for multiple trials
for i in range(num_tries):
    # Draw from the noise distribution, which is diffusion for time T with noise strength 1
    x0 = np.random.normal(loc=0, scale=T)
    # Simulate reverse diffusion
    x, t = reverse_diffusion_1D(x0, noise_strength_fn, score_fn, T, nsteps, dt)
    # Plot the trajectory
    plt.plot(t, x, label=f'Trial {i+1}')  # Adding a label for each trial
# Labeling the plot
plt.xlabel('Time', fontsize=20)
plt.ylabel('Sample Value ($x$)', fontsize=20)
# Title of the plot
plt.title('Reverse Diffusion Visualized', fontsize=20)
# Adding a legend to identify each trial
plt.legend()
# Show the plot
plt.show()

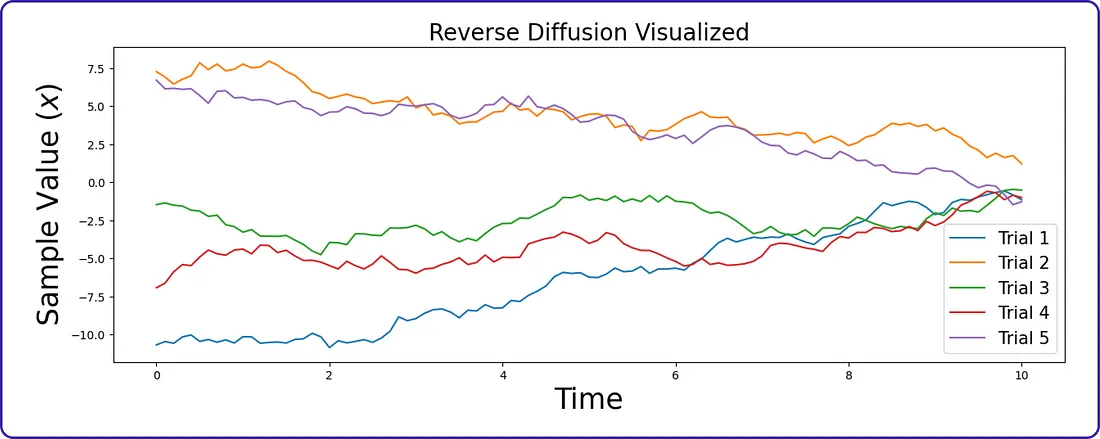
这个可视化表明，在前向扩散过程从复杂的数据分布中创建出一个样本之后（如在之前的前向扩散可视化中所见），逆向扩散过程通过一系列逆变换将其映射回简单分布。

学习评分函数

在现实世界情景中，我们初始时并不知道评分函数，我们的目标是学习它。一种方法涉及训练神经网络，使用去噪目标来‘去噪’样本。

在这里，p0​(x0​)代表我们的目标分布（例如，汽车和猫的图像），而x(noised)​表示经过单次向前扩散步骤后来自目标分布x0​的样本。换句更简单的话说，[ x(noised)​ − x0 ]​本质上是一个呈正态分布的随机变量。

用更接近实际实现的方式表达相同的想法：

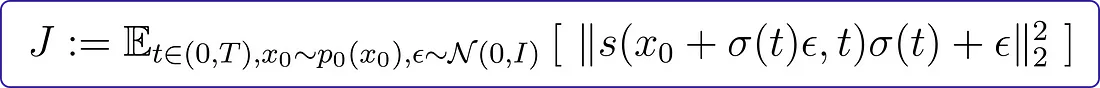
理解我们的目标是预测在扩散过程中的每一个时间点t，对样本的每一个部分添加的噪声量的概念非常重要，这适用于我们原始分布（汽车、猫等）中的每一个x0​。

在这些表达式中：

• J代表去噪目标。
• E表示期望值。
• t代表时间参数。
• x0​是目标分布p0​(x0​)的一个样本。
• x(noised)​代表目标分布样本x0​在一个前向扩散步骤之后的状态。
• s(⋅,⋅)代表分数函数。
• σ(t)是时间的函数。
• ϵ是一个服从正态分布的随机变量。

到目前为止，我们已经涵盖了前向扩散和后向扩散的基础知识，并且探索了如何学习我们的分数函数。

神经网络的时间嵌入

学习分数函数就像将随机噪声转换成有意义的东西。为此，我们使用一个神经网络来近似分数函数。在处理图像时，我们希望我们的神经网络与它们以及我们希望学习的以时间为依赖的分数函数能够很好地协作，我们需要一种方法来确保我们的神经网络能够准确地响应时间变化。为了实现这一点，我们可以使用时间嵌入。

我们不仅仅向网络提供一个时间值，而是使用许多正弦特征来表示当前时间。通过提供时间的不同表示，我们旨在增强网络对时间变化的适应能力。这种方法使我们能够有效地学习一个与时间相关的分数函数s(x,t)。

为了使我们的神经网络能够与时间交互，我们需要创建两个模块。

# Define a module for Gaussian random features used to encode time steps.
class GaussianFourierProjection(nn.Module):
    def __init__(self, embed_dim, scale=30.):
        """
        Parameters:
        - embed_dim: Dimensionality of the embedding (output dimension)
        - scale: Scaling factor for random weights (frequencies)
        """
        super().__init__()
        # Randomly sample weights (frequencies) during initialization.
        # These weights (frequencies) are fixed during optimization and are not trainable.
        self.W = nn.Parameter(torch.randn(embed_dim // 2) * scale, requires_grad=False)
    def forward(self, x):
        """
        Parameters:
        - x: Input tensor representing time steps
        """
        # Calculate the cosine and sine projections: Cosine(2 pi freq x), Sine(2 pi freq x)
        x_proj = x[:, None] * self.W[None, :] * 2 * np.pi
        # Concatenate the sine and cosine projections along the last dimension
        return torch.cat([torch.sin(x_proj), torch.cos(x_proj)], dim=-1)

该GaussianFourierProjection函数旨在创建一个用于生成高斯随机特征的模块，该模块将用于表示我们上下文中的时间步长。当我们使用该模块时，它会生成在整个优化过程中保持固定的随机频率。x一旦我们向模块提供输入张量，它就会通过x与这些预定义的随机频率相乘来计算正弦和余弦投影。然后将这些投影连接起来形成输入的特征表示，从而有效地捕获时间模式。该模块对我们的任务很有价值，我们的目标是将与时间相关的信息合并到我们的神经网络中。

# Define a module for a fully connected layer that reshapes outputs to feature maps.
class Dense(nn.Module):
    def __init__(self, input_dim, output_dim):
        """
        Parameters:
        - input_dim: Dimensionality of the input features
        - output_dim: Dimensionality of the output features
        """
        super().__init__()
        # Define a fully connected layer
        self.dense = nn.Linear(input_dim, output_dim)
    def forward(self, x):
        """
        Parameters:
        - x: Input tensor
        Returns:
        - Output tensor after passing through the fully connected layer
          and reshaping to a 4D tensor (feature map)
        """
        # Apply the fully connected layer and reshape the output to a 4D tensor
        return self.dense(x)[..., None, None]
        # This broadcasts the 2D tensor to a 4D tensor, adding the same value across space.

Dense模块旨在将全连接层的输出重塑成4D张量，有效地将其转换成一个特征图。该模块接受输入特征的维数（input_dim）和希望得到的输出特征的维数（output_dim）作为输入。在前向传播过程中，输入张量x通过全连接层（self.dense(x)）处理，输出被重塑成4D张量，方法是在末尾添加两个单例维度（[..., None, None]）。这个重塑操作有效地将输出转换成适合在卷积层中进一步处理的特征图。该操作通过在空间维度上添加相同的值，将2D张量广播到4D张量。

现在我们已经建立了两个模块用于将时间交互整合到我们的神经网络中，是时候开始编码主神经网络了。

编写带有串联操作的U-Net架构

在处理图像时，我们的神经网络需要与图像无缝配合，并捕捉与图像相关的固有特征。

我们选择了U-Net架构，它结合了类CNN结构和缩放/扩展操作。这种组合有助于网络关注不同空间尺度上的图像特征。

# Define a time-dependent score-based model built upon the U-Net architecture.
class UNet(nn.Module):
    def __init__(self, marginal_prob_std, channels=[32, 64, 128, 256], embed_dim=256):
        """
        Initialize a time-dependent score-based network.
        Parameters:
        - marginal_prob_std: A function that takes time t and gives the standard deviation
          of the perturbation kernel p_{0t}(x(t) | x(0)).
        - channels: The number of channels for feature maps of each resolution.
        - embed_dim: The dimensionality of Gaussian random feature embeddings.
        """
        super().__init__()
        # Gaussian random feature embedding layer for time
        self.time_embed = nn.Sequential(
            GaussianFourierProjection(embed_dim=embed_dim),
            nn.Linear(embed_dim, embed_dim)
        )
        # Encoding layers where the resolution decreases
        self.conv1 = nn.Conv2d(1, channels[0], 3, stride=1, bias=False)
        self.dense1 = Dense(embed_dim, channels[0])
        self.gnorm1 = nn.GroupNorm(4, num_channels=channels[0])
        self.conv2 = nn.Conv2d(channels[0], channels[1], 3, stride=2, bias=False)
        self.dense2 = Dense(embed_dim, channels[1])
        self.gnorm2 = nn.GroupNorm(32, num_channels=channels[1])
        # Additional encoding layers (copied from the original code)
        self.conv3 = nn.Conv2d(channels[1], channels[2], 3, stride=2, bias=False)
        self.dense3 = Dense(embed_dim, channels[2])
        self.gnorm3 = nn.GroupNorm(32, num_channels=channels[2])
        self.conv4 = nn.Conv2d(channels[2], channels[3], 3, stride=2, bias=False)
        self.dense4 = Dense(embed_dim, channels[3])
        self.gnorm4 = nn.GroupNorm(32, num_channels=channels[3])
        # Decoding layers where the resolution increases
        self.tconv4 = nn.ConvTranspose2d(channels[3], channels[2], 3, stride=2, bias=False)
        self.dense5 = Dense(embed_dim, channels[2])
        self.tgnorm4 = nn.GroupNorm(32, num_channels=channels[2])
        self.tconv3 = nn.ConvTranspose2d(channels[2] + channels[2], channels[1], 3, stride=2, bias=False, output_padding=1)
        self.dense6 = Dense(embed_dim, channels[1])
        self.tgnorm3 = nn.GroupNorm(32, num_channels=channels[1])
        self.tconv2 = nn.ConvTranspose2d(channels[1] + channels[1], channels[0], 3, stride=2, bias=False, output_padding=1)
        self.dense7 = Dense(embed_dim, channels[0])
        self.tgnorm2 = nn.GroupNorm(32, num_channels=channels[0])
        self.tconv1 = nn.ConvTranspose2d(channels[0] + channels[0], 1, 3, stride=1)
        # The swish activation function
        self.act = lambda x: x * torch.sigmoid(x)
        self.marginal_prob_std = marginal_prob_std
    def forward(self, x, t, y=None):
        """
        Parameters:
        - x: Input tensor
        - t: Time tensor
        - y: Target tensor (not used in this forward pass)
        Returns:
        - h: Output tensor after passing through the U-Net architecture
        """
        # Obtain the Gaussian random feature embedding for t
        embed = self.act(self.time_embed(t))
        # Encoding path
        h1 = self.conv1(x) + self.dense1(embed)
        h1 = self.act(self.gnorm1(h1))
        h2 = self.conv2(h1) + self.dense2(embed)
        h2 = self.act(self.gnorm2(h2))
        # Additional encoding path layers (copied from the original code)
        h3 = self.conv3(h2) + self.dense3(embed)
        h3 = self.act(self.gnorm3(h3))
        h4 = self.conv4(h3) + self.dense4(embed)
        h4 = self.act(self.gnorm4(h4))
        # Decoding path
        h = self.tconv4(h4)
        h += self.dense5(embed)
        h = self.act(self.tgnorm4(h))
        h = self.tconv3(torch.cat([h, h3], dim=1))
        h += self.dense6(embed)
        h = self.act(self.tgnorm3(h))
        h = self.tconv2(torch.cat([h, h2], dim=1))
        h += self.dense7(embed)
        h = self.act(self.tgnorm2(h))
        h = self.tconv1(torch.cat([h, h1], dim=1))
        # Normalize output
        h = h / self.marginal_prob_std(t)[:, None, None, None]
        return h

我们创建了一个模型，能够理解事物随时间变化的方式。它采用了一种特殊结构，称为U型网络（U-Net）。想象你有一张起始图片，你想看到它在不同时间点上的变化。模型学习这些变化中的模式和细节。代码定义了这种学习如何发生，使用了各种层和计算。它确保输出，或者说生成的图片，根据时间信息进行恰当调整。这就像一个智能工具，用于理解和预测事物在视觉上的演变。

在U型网络模型的架构中，张量的形状随着信息通过编码和解码路径而变化。在编码路径中，涉及到下采样，张量在每一个卷积层上经历形状缩减 —— 依次是h1、h2、h3和h4。在解码路径中，转置卷积层开始恢复空间信息。张量h开始恢复原始的空间尺寸，在每一步 (h4到h1) 中，从早期层加回的特征有助于上采样。最后，由h代表的最后一层产出输出，并且标准化步骤确保生成图像的适当缩放。张量形状的具体情况取决于卷积层中使用的滤波器大小、步幅和填充等因素，这些因素塑造了模型捕获和重建细节的能力。

用加法编码U型网络架构

扩散模型可以很好地与各种架构选择协作。在我们之前构建的模型中，我们通过拼接来结合下块的张量，用于跳跃连接。在我们即将编码的模型中，我们将简单地添加来自下块的张量以实现跳跃连接。

# Define a time-dependent score-based model built upon the U-Net architecture.
class UNet_res(nn.Module):
    def __init__(self, marginal_prob_std, channels=[32, 64, 128, 256], embed_dim=256):
        """
        Parameters:
        - marginal_prob_std: A function that takes time t and gives the standard deviation
          of the perturbation kernel p_{0t}(x(t) | x(0)).
        - channels: The number of channels for feature maps of each resolution.
        - embed_dim: The dimensionality of Gaussian random feature embeddings.
        """
        super().__init__()
        # Gaussian random feature embedding layer for time
        self.time_embed = nn.Sequential(
            GaussianFourierProjection(embed_dim=embed_dim),
            nn.Linear(embed_dim, embed_dim)
        )
        # Encoding layers where the resolution decreases
        self.conv1 = nn.Conv2d(1, channels[0], 3, stride=1, bias=False)
        self.dense1 = Dense(embed_dim, channels[0])
        self.gnorm1 = nn.GroupNorm(4, num_channels=channels[0])
        self.conv2 = nn.Conv2d(channels[0], channels[1], 3, stride=2, bias=False)
        self.dense2 = Dense(embed_dim, channels[1])
        self.gnorm2 = nn.GroupNorm(32, num_channels=channels[1])
        self.conv3 = nn.Conv2d(channels[1], channels[2], 3, stride=2, bias=False)
        self.dense3 = Dense(embed_dim, channels[2])
        self.gnorm3 = nn.GroupNorm(32, num_channels=channels[2])
        self.conv4 = nn.Conv2d(channels[2], channels[3], 3, stride=2, bias=False)
        self.dense4 = Dense(embed_dim, channels[3])
        self.gnorm4 = nn.GroupNorm(32, num_channels=channels[3])
        # Decoding layers where the resolution increases
        self.tconv4 = nn.ConvTranspose2d(channels[3], channels[2], 3, stride=2, bias=False)
        self.dense5 = Dense(embed_dim, channels[2])
        self.tgnorm4 = nn.GroupNorm(32, num_channels=channels[2])
        self.tconv3 = nn.ConvTranspose2d(channels[2], channels[1], 3, stride=2, bias=False, output_padding=1)
        self.dense6 = Dense(embed_dim, channels[1])
        self.tgnorm3 = nn.GroupNorm(32, num_channels=channels[1])
        self.tconv2 = nn.ConvTranspose2d(channels[1], channels[0], 3, stride=2, bias=False, output_padding=1)
        self.dense7 = Dense(embed_dim, channels[0])
        self.tgnorm2 = nn.GroupNorm(32, num_channels=channels[0])
        self.tconv1 = nn.ConvTranspose2d(channels[0], 1, 3, stride=1)
        # The swish activation function
        self.act = lambda x: x * torch.sigmoid(x)
        self.marginal_prob_std = marginal_prob_std
    def forward(self, x, t, y=None):
        """
        Parameters:
        - x: Input tensor
        - t: Time tensor
        - y: Target tensor (not used in this forward pass)
        Returns:
        - h: Output tensor after passing through the U-Net architecture
        """
        # Obtain the Gaussian random feature embedding for t
        embed = self.act(self.time_embed(t))
        # Encoding path
        h1 = self.conv1(x) + self.dense1(embed)
        h1 = self.act(self.gnorm1(h1))
        h2 = self.conv2(h1) + self.dense2(embed)
        h2 = self.act(self.gnorm2(h2))
        h3 = self.conv3(h2) + self.dense3(embed)
        h3 = self.act(self.gnorm3(h3))
        h4 = self.conv4(h3) + self.dense4(embed)
        h4 = self.act(self.gnorm4(h4))
        # Decoding path
        h = self.tconv4(h4)
        h += self.dense5(embed)
        h = self.act(self.tgnorm4(h))
        h = self.tconv3(h + h3)
        h += self.dense6(embed)
        h = self.act(self.tgnorm3(h))
        h = self.tconv2(h + h2)
        h += self.dense7(embed)
        h = self.act(self.tgnorm2(h))
        h = self.tconv1(h + h1)
        # Normalize output
        h = h / self.marginal_prob_std(t)[:, None, None, None]
        return h

我们刚刚编码的UNet_res模型是标准UNet模型的一个变种。虽然这两种模型都遵循U-Net架构，但关键区别在于跳跃连接的实现方式。在原始的UNet模型中，跳跃连接是将编码路径上的张量与解码路径上的张量进行拼接。然而，在UNet_res模型中，跳跃连接涉及直接将编码路径上的张量加到解码路径上对应的张量上。这种跳跃连接策略的变化可能会影响信息流和不同分辨率级别之间的交互，从而可能影响模型捕获数据中的特征和依赖关系的能力。

具有指数噪声的前向扩散过程

我们将定义具体的前向扩散过程：

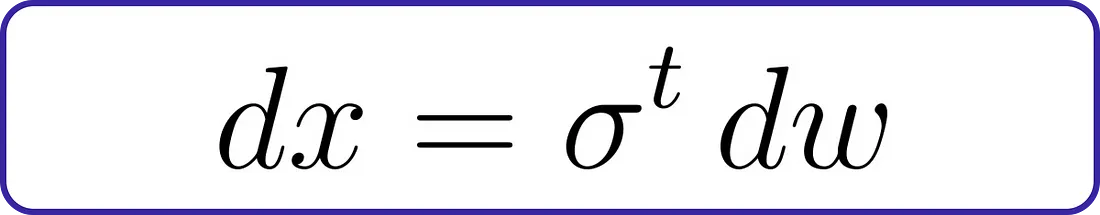
这个公式代表了一个动态系统，在该系统中，随着噪声（dw）的引入，变量x随时间（t）变化。噪声水平由参数σ决定，并随着时间的推移呈指数级增加。

给定这个过程和一个初始值x(0)，我们可以找到x(t)的解析解。

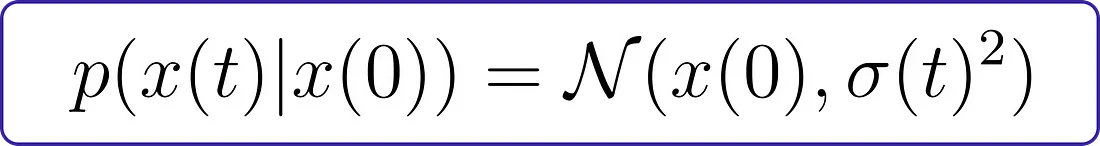
在这个上下文中，σ(t) 被称为边际标准差。本质上，它代表了在给定初始值 x(0) 的情况下 x(t) 分布的变异性。

对于我们特定的情况，边际标准差是这样计算的：

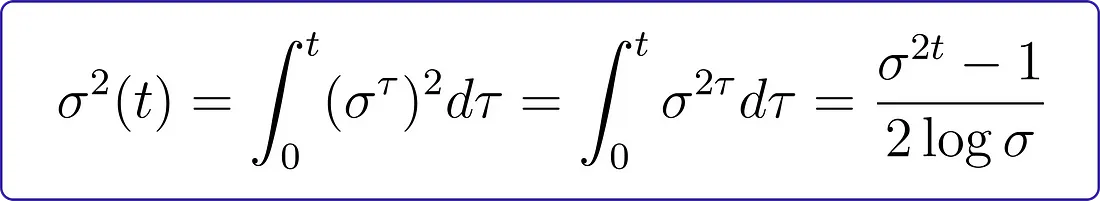
这个公式提供了对噪声水平（σ）如何随时间演变以及如何影响系统可变性。

# Using GPU
device = "cuda"
# Marginal Probability Standard Deviation Function
def marginal_prob_std(t, sigma):
    """
    Compute the mean and standard deviation of $p_{0t}(x(t) | x(0))$.
    Parameters:
    - t: A vector of time steps.
    - sigma: The $\sigma$ in our SDE.
    Returns:
    - The standard deviation.
    """
    # Convert time steps to a PyTorch tensor
    t = torch.tensor(t, device=device)
    
    # Calculate and return the standard deviation based on the given formula
    return torch.sqrt((sigma**(2 * t) - 1.) / 2. / np.log(sigma))

现在我们已经编写了边际概率标准差的函数，我们可以类似地编写扩散系数的代码。

# Using GPU
device = "cuda"
def diffusion_coeff(t, sigma):
    """
    Compute the diffusion coefficient of our SDE.
    Parameters:
    - t: A vector of time steps.
    - sigma: The $\sigma$ in our SDE.
    Returns:
    - The vector of diffusion coefficients.
    """
    # Calculate and return the diffusion coefficients based on the given formula
    return torch.tensor(sigma**t, device=device)
现在我们将边际概率标准差和扩散系数初始化为 sigma 25。
# Sigma Value
sigma =  25.0
# marginal probability standard
marginal_prob_std_fn = functools.partial(marginal_prob_std, sigma=sigma)
# diffusion coefficient
diffusion_coeff_fn = functools.partial(diffusion_coeff, sigma=sigma)

在编写了两个模块之后，是时候为我们的稳定扩散架构开发损失函数了。

编写损失函数

现在，我们要把之前制作的U-Net和一个学习得分函数的方法结合起来。我们将创建一个损失函数并训练神经网络。

def loss_fn(model, x, marginal_prob_std, eps=1e-5):
    """
    The loss function for training score-based generative models.
    Parameters:
    - model: A PyTorch model instance that represents a time-dependent score-based model.
    - x: A mini-batch of training data.
    - marginal_prob_std: A function that gives the standard deviation of the perturbation kernel.
    - eps: A tolerance value for numerical stability.
    """
    # Sample time uniformly in the range (eps, 1-eps)
    random_t = torch.rand(x.shape[0], device=x.device) * (1. - 2 * eps) + eps
    # Find the noise std at the sampled time `t`
    std = marginal_prob_std(random_t)
    
    # Generate normally distributed noise
    z = torch.randn_like(x)
    
    # Perturb the input data with the generated noise
    perturbed_x = x + z * std[:, None, None, None]
    
    # Get the score from the model using the perturbed data and time
    score = model(perturbed_x, random_t)
    
    # Calculate the loss based on the score and noise
    loss = torch.mean(torch.sum((score * std[:, None, None, None] + z)**2, dim=(1, 2, 3)))
    
    return loss

这个损失函数用于在训练过程中计算我们的模型有多错误。它包括随机选择一个时间点，获取噪声水平，将这个噪声加到我们的数据上，然后检查模型预测与现实之间的偏差有多大。目标是在训练过程中减少这种误差。

编写采样器

稳定扩散通过从一个完全随机的图像开始来创建图像。然后，噪声预测器猜测图像的噪声水平，并将猜测出的噪声从图像中去除。整个循环重复数次，最终得到一个清晰的图像。

这个清理过程被称为“采样”，因为稳定扩散在每一步都产生一个新的图像样本。它创建这些样本的方式被称为“采样器”或“采样方法”。

稳定扩散有多种创建图像样本的选项，我们将使用的一种方法是Euler-Maruyama方法，也称为Euler方法。

# number of steps
num_steps = 500
def Euler_Maruyama_sampler(score_model,
                           marginal_prob_std,
                           diffusion_coeff,
                           batch_size=64,
                           x_shape=(1, 28, 28),
                           num_steps=num_steps,
                           device='cuda',
                           eps=1e-3, y=None):
    """
    Generate samples from score-based models with the Euler-Maruyama solver.
    Parameters:
    - score_model: A PyTorch model that represents the time-dependent score-based model.
    - marginal_prob_std: A function that gives the standard deviation of the perturbation kernel.
    - diffusion_coeff: A function that gives the diffusion coefficient of the SDE.
    - batch_size: The number of samplers to generate by calling this function once.
    - x_shape: The shape of the samples.
    - num_steps: The number of sampling steps, equivalent to the number of discretized time steps.
    - device: 'cuda' for running on GPUs, and 'cpu' for running on CPUs.
    - eps: The smallest time step for numerical stability.
    - y: Target tensor (not used in this function).
    Returns:
    - Samples.
    """
    # Initialize time and the initial sample
    t = torch.ones(batch_size, device=device)
    init_x = torch.randn(batch_size, *x_shape, device=device) * marginal_prob_std(t)[:, None, None, None]
    
    # Generate time steps
    time_steps = torch.linspace(1., eps, num_steps, device=device)
    step_size = time_steps[0] - time_steps[1]
    x = init_x
    
    # Sample using Euler-Maruyama method
    with torch.no_grad():
        for time_step in tqdm(time_steps):
            batch_time_step = torch.ones(batch_size, device=device) * time_step
            g = diffusion_coeff(batch_time_step)
            mean_x = x + (g**2)[:, None, None, None] * score_model(x, batch_time_step, y=y) * step_size
            x = mean_x + torch.sqrt(step_size) * g[:, None, None, None] * torch.randn_like(x)
    
    # Do not include any noise in the last sampling step.
    return mean_x

这个函数使用Euler-Maruyama方法产生图像样本，结合了基于评分的模型、噪声标准偏差的函数以及扩散系数。它迭代地应用这个方法多个指定的步骤，返回最终生成的样本集。

训练U-Net级联架构

我们开发了两种U-Net架构：一种使用加法，另一种使用级联。为了开始训练，我们将使用基于级联的U-Net架构，并设置以下超参数：训练50个周期，迷你批次大小为2048，学习率为5e-4。训练将在MNIST数据集上进行。

# Define the score-based model and move it to the specified device
score_model = torch.nn.DataParallel(UNet(marginal_prob_std=marginal_prob_std_fn))
score_model = score_model.to(device)
# Number of training epochs
n_epochs = 50
# Size of a mini-batch
batch_size = 2048
# Learning rate
lr = 5e-4
# Load the MNIST dataset and create a data loader
dataset = MNIST('.', train=True, transform=transforms.ToTensor(), download=True)
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=4)
# Define the Adam optimizer for training the model
optimizer = Adam(score_model.parameters(), lr=lr)
# Progress bar for epochs
tqdm_epoch = trange(n_epochs)
for epoch in tqdm_epoch:
    avg_loss = 0.
    num_items = 0
    # Iterate through mini-batches in the data loader
    for x, y in tqdm(data_loader):
        x = x.to(device)
        # Calculate the loss and perform backpropagation
        loss = loss_fn(score_model, x, marginal_prob_std_fn)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        avg_loss += loss.item() * x.shape[0]
        num_items += x.shape[0]
    # Print the averaged training loss for the current epoch
    tqdm_epoch.set_description('Average Loss: {:5f}'.format(avg_loss / num_items))
    # Save the model checkpoint after each epoch of training
    torch.save(score_model.state_dict(), 'ckpt.pth')

执行训练代码后，整个训练过程预计每个周期大约完成7分钟。在各个周期中观察到的平均损失是34.128，训练好的模型将会保存在当前目录下，文件名为“ckpt.pth”。

让我们来可视化基于连接的U-Net架构的结果。需要注意的是，我们还没有开始开发一个系统，通过输入提示语来生成特定结果。目前的可视化仅仅基于随机输入。

# Load the pre-trained checkpoint from disk.
device = 'cuda'
# Load the pre-trained model checkpoint
ckpt = torch.load('ckpt.pth', map_location=device)
score_model.load_state_dict(ckpt)
# Set sample batch size and number of steps
sample_batch_size = 64
num_steps = 500
# Choose the Euler-Maruyama sampler
sampler = Euler_Maruyama_sampler
# Generate samples using the specified sampler
samples = sampler(score_model,
                  marginal_prob_std_fn,
                  diffusion_coeff_fn,
                  sample_batch_size,
                  num_steps=num_steps,
                  device=device,
                  y=None)
# Clip samples to be in the range [0, 1]
samples = samples.clamp(0.0, 1.0)
# Visualize the generated samples
%matplotlib inline
import matplotlib.pyplot as plt
sample_grid = make_grid(samples, nrow=int(np.sqrt(sample_batch_size)))
# Plot the sample grid
plt.figure(figsize=(6, 6))
plt.axis('off')
plt.imshow(sample_grid.permute(1, 2, 0).cpu(), vmin=0., vmax=1.)
plt.show()

目前的结果并不令人满意，因为要清楚地辨识出任何数字都很有挑战性。

训练U-Net增强架构

具有连接操作的U-Net架构表现不佳。然而，让我们继续进行基于加法操作的U-Net架构的训练，并确定它是否能带来更好的结果。

我们将使用以下超参数：训练75个周期，小批量数据大小为1024，学习率为10e-3。训练将在MNIST数据集上进行。

# Initialize the alternate U-Net model for training.
score_model = torch.nn.DataParallel(UNet_res(marginal_prob_std=marginal_prob_std_fn))
score_model = score_model.to(device)
# Set the number of training epochs, mini-batch size, and learning rate.
n_epochs = 75
batch_size = 1024
lr = 1e-3
# Load the MNIST dataset for training.
dataset = MNIST('.', train=True, transform=transforms.ToTensor(), download=True)
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=4)
# Initialize the Adam optimizer with the specified learning rate.
optimizer = Adam(score_model.parameters(), lr=lr)
# Learning rate scheduler to adjust the learning rate during training.
scheduler = LambdaLR(optimizer, lr_lambda=lambda epoch: max(0.2, 0.98 ** epoch))
# Training loop over epochs.
tqdm_epoch = trange(n_epochs)
for epoch in tqdm_epoch:
    avg_loss = 0.
    num_items = 0
    # Iterate over mini-batches in the training data loader.
    for x, y in data_loader:
        x = x.to(device)
        # Compute the loss for the current mini-batch.
        loss = loss_fn(score_model, x, marginal_prob_std_fn)
        # Zero the gradients, backpropagate, and update the model parameters.
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        # Accumulate the total loss and the number of processed items.
        avg_loss += loss.item() * x.shape[0]
        num_items += x.shape[0]
    
    # Adjust the learning rate using the scheduler.
    scheduler.step()
    lr_current = scheduler.get_last_lr()[0]
    
    # Print the average loss and learning rate for the current epoch.
    print('{} Average Loss: {:5f} lr {:.1e}'.format(epoch, avg_loss / num_items, lr_current))
    tqdm_epoch.set_description('Average Loss: {:5f}'.format(avg_loss / num_items))
    
    # Save the model checkpoint after each epoch of training.
    torch.save(score_model.state_dict(), 'ckpt_res.pth')

当执行训练代码后，整个训练过程预计每个时代约需11分钟才能完成。各个时代观测到的平均损失是24.585，训练后的模型将以“ckpt_res.pth”为文件名保存在当前目录中。

让我们来可视化我们基于加法的U-Net架构的结果。

# Load the pre-trained checkpoint from disk.
device = 'cuda'
# Load the pre-trained model checkpoint
ckpt = torch.load('ckpt_res.pth', map_location=device)
score_model.load_state_dict(ckpt)
# Set sample batch size and number of steps
sample_batch_size = 64
num_steps = 500
# Choose the Euler-Maruyama sampler
sampler = Euler_Maruyama_sampler
# Generate samples using the specified sampler
samples = sampler(score_model,
                  marginal_prob_std_fn,
                  diffusion_coeff_fn,
                  sample_batch_size,
                  num_steps=num_steps,
                  device=device,
                  y=None)
# Clip samples to be in the range [0, 1]
samples = samples.clamp(0.0, 1.0)
# Visualize the generated samples
%matplotlib inline
import matplotlib.pyplot as plt
sample_grid = make_grid(samples, nrow=int(np.sqrt(sample_batch_size)))
# Plot the sample grid
plt.figure(figsize=(6, 6))
plt.axis('off')
plt.imshow(sample_grid.permute(1, 2, 0).cpu(), vmin=0., vmax=1.)
plt.show()

基于加法的U-Net架构显示出比拼接架构更好的性能。它能够更清晰地识别图像中的数字，并且此外，在使用这种架构的培训过程中，损失一致地减少。

直到现在，我们的架构生成了随机图像样本。然而，目标是使我们的稳定扩散模型能够手绘出提供作为输入的指定数字。

构建注意力层

在创建注意力模型时，我们通常有三个主要部分：

1. 交叉注意力：处理序列的自我/交叉注意力。
2. 变压器模块：结合了注意力与用于处理的神经网络。
3. 空间变压器：将U-Net中的空间张量转换成序列形式，反之亦然。

让我们用更简单的术语来解释注意力模型背后的数学原理。在QKV（查询-键-值）注意力中，我们将查询、键和值表示为向量。这些向量帮助我们将翻译任务的一侧的单词或图像与另一侧连接。

这些向量（q，k，v）与编码器的隐藏状态向量（e）和解码器的隐藏状态向量（h）存在线性关系：

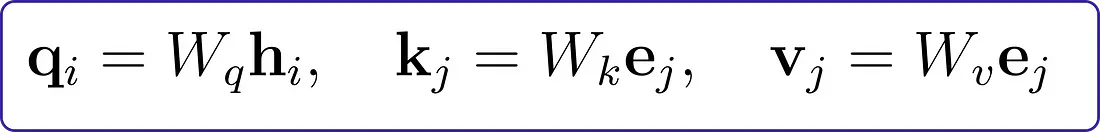
为了决定将“注意力”投向何处，我们会计算每个键（k）与查询（q）之间的内积（相似度）。为了确保这些值是合理的，我们通过查询向量（qi）的长度来对它们进行归一化。

通过对这些值应用softmax函数，我们得到了最终的注意力分布：

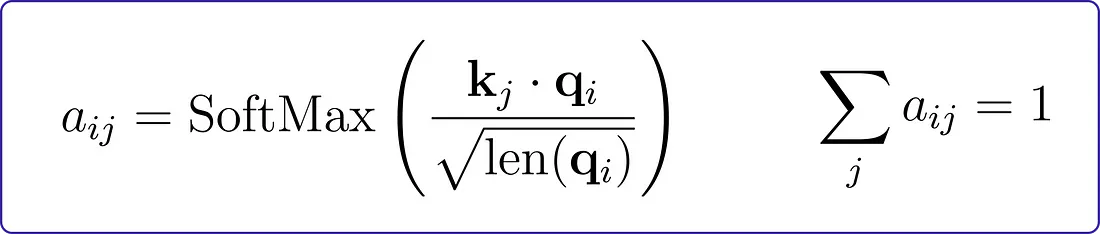
这种注意力分配有助于挑选出相关的特征组合。例如，当将英语短语“This is cool”翻译成法语时，正确的答案（“c’est cool”）涉及到同时关注两个单词，而不是分别逐个单词进行翻译。在数学上，我们使用注意力分布来加权这些值（vj）：

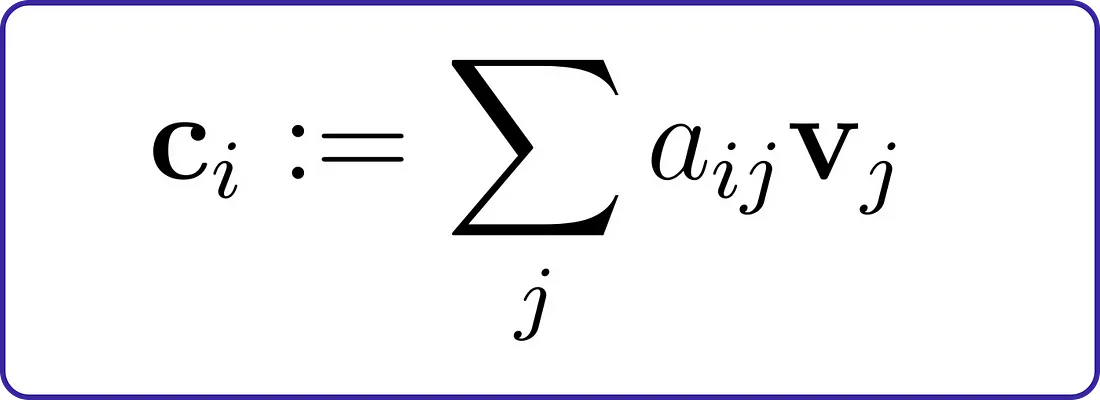
现在我们已经理解了注意力机制的基础知识以及我们需要构建的三个注意力模块，让我们开始编写它们。

让我们从编写第一个注意力层开始，即CrossAttention。

class CrossAttention(nn.Module):
    def __init__(self, embed_dim, hidden_dim, context_dim=None, num_heads=1):
        """
        Initialize the CrossAttention module.
        Parameters:
        - embed_dim: The dimensionality of the output embeddings.
        - hidden_dim: The dimensionality of the hidden representations.
        - context_dim: The dimensionality of the context representations (if not self attention).
        - num_heads: Number of attention heads (currently supports 1 head).
        Note: For simplicity reasons, the implementation assumes 1-head attention.
        Feel free to implement multi-head attention using fancy tensor manipulations.
        """
        super(CrossAttention, self).__init__()
        self.hidden_dim = hidden_dim
        self.context_dim = context_dim
        self.embed_dim = embed_dim
        # Linear layer for query projection
        self.query = nn.Linear(hidden_dim, embed_dim, bias=False)
        
        # Check if self-attention or cross-attention
        if context_dim is None:
            self.self_attn = True
            self.key = nn.Linear(hidden_dim, embed_dim, bias=False)
            self.value = nn.Linear(hidden_dim, hidden_dim, bias=False)
        else:
            self.self_attn = False
            self.key = nn.Linear(context_dim, embed_dim, bias=False)
            self.value = nn.Linear(context_dim, hidden_dim, bias=False)
    def forward(self, tokens, context=None):
        """
        Forward pass of the CrossAttention module.
        Parameters:
        - tokens: Input tokens with shape [batch, sequence_len, hidden_dim].
        - context: Context information with shape [batch, context_seq_len, context_dim].
                   If self_attn is True, context is ignored.
        Returns:
        - ctx_vecs: Context vectors after attention with shape [batch, sequence_len, embed_dim].
        """
        if self.self_attn:
            # Self-attention case
            Q = self.query(tokens)
            K = self.key(tokens)
            V = self.value(tokens)
        else:
            # Cross-attention case
            Q = self.query(tokens)
            K = self.key(context)
            V = self.value(context)
        # Compute score matrices, attention matrices, and context vectors
        scoremats = torch.einsum("BTH,BSH->BTS", Q, K)  # Inner product of Q and K, a tensor
        attnmats = F.softmax(scoremats / math.sqrt(self.embed_dim), dim=-1)  # Softmax of scoremats
        ctx_vecs = torch.einsum("BTS,BSH->BTH", attnmats, V)  # Weighted average value vectors by attnmats
        return ctx_vecs

CrossAttention 类是一个为处理神经网络中的注意力机制而设计的模块。它接收输入令牌，并且可选地接收上下文信息。如果用于自注意力，它专注于输入令牌之内的关系。在交叉注意力的情况下，它考虑输入令牌和上下文信息之间的交互作用。该模块采用线性投影来进行查询（query）、键（key）和值（value）的转换。它计算得分矩阵，应用 softmax 函数获得注意力权重，并通过基于注意力权重合并加权后的值来计算上下文向量。这一机制允许网络有选择性地关注输入或上下文的不同部分，帮助在学习过程中捕获相关信息。forward 方法实现了这些操作，返回经过注意力处理后的上下文向量。

让我们接着讨论第二个注意力层，称为 TransformerBlock。

class TransformerBlock(nn.Module):
    """The transformer block that combines self-attn, cross-attn, and feed forward neural net"""
    def __init__(self, hidden_dim, context_dim):
        """
        Initialize the TransformerBlock.
        Parameters:
        - hidden_dim: The dimensionality of the hidden state.
        - context_dim: The dimensionality of the context tensor.
        Note: For simplicity, the self-attn and cross-attn use the same hidden_dim.
        """
        super(TransformerBlock, self).__init__()
        # Self-attention module
        self.attn_self = CrossAttention(hidden_dim, hidden_dim)
        # Cross-attention module
        self.attn_cross = CrossAttention(hidden_dim, hidden_dim, context_dim)
        # Layer normalization modules
        self.norm1 = nn.LayerNorm(hidden_dim)
        self.norm2 = nn.LayerNorm(hidden_dim)
        self.norm3 = nn.LayerNorm(hidden_dim)
        # Implement a 2-layer MLP with K * hidden_dim hidden units, and nn.GELU nonlinearity
        self.ffn = nn.Sequential(
            nn.Linear(hidden_dim, 3 * hidden_dim),
            nn.GELU(),
            nn.Linear(3 * hidden_dim, hidden_dim)
        )
    def forward(self, x, context=None):
        """
        Forward pass of the TransformerBlock.
        Parameters:
        - x: Input tensor with shape [batch, sequence_len, hidden_dim].
        - context: Context tensor with shape [batch, context_seq_len, context_dim].
        Returns:
        - x: Output tensor after passing through the TransformerBlock.
        """
        # Apply self-attention with layer normalization and residual connection
        x = self.attn_self(self.norm1(x)) + x
        # Apply cross-attention with layer normalization and residual connection
        x = self.attn_cross(self.norm2(x), context=context) + x
        # Apply feed forward neural network with layer normalization and residual connection
        x = self.ffn(self.norm3(x)) + x
        return x

TransformerBlock类代表了在Transformer模型中的一个构建块，它集成了自注意力(self-attention)、交叉注意力(cross-attention)和一个前馈神经网络。它接受形状为[batch, sequence_len, hidden_dim]的输入张量，并且可选地接受一个形状为[batch, context_seq_len, context_dim]的上下文张量。自注意力和交叉注意力模块之后是层归一化(layer normalization)和残差连接。另外，该模块包含了一个带有GELU非线性激活函数的两层MLP，用于进一步的非线性变换。在通过TransformerBlock处理后得到输出。

让我们继续进行最后一层注意力层，称为SpatialTransformer。

class SpatialTransformer(nn.Module):
    def __init__(self, hidden_dim, context_dim):
        """
        Initialize the SpatialTransformer.
        Parameters:
        - hidden_dim: The dimensionality of the hidden state.
        - context_dim: The dimensionality of the context tensor.
        """
        super(SpatialTransformer, self).__init__()
        
        # TransformerBlock for spatial transformation
        self.transformer = TransformerBlock(hidden_dim, context_dim)
    def forward(self, x, context=None):
        """
        Forward pass of the SpatialTransformer.
        Parameters:
        - x: Input tensor with shape [batch, channels, height, width].
        - context: Context tensor with shape [batch, context_seq_len, context_dim].
        Returns:
        - x: Output tensor after applying spatial transformation.
        """
        b, c, h, w = x.shape
        x_in = x
        # Combine the spatial dimensions and move the channel dimension to the end
        x = rearrange(x, "b c h w -> b (h w) c")
        # Apply the sequence transformer
        x = self.transformer(x, context)
        # Reverse the process
        x = rearrange(x, 'b (h w) c -> b c h w', h=h, w=w)
        # Residue connection
        return x + x_in

现在，你可以将空间变换器层(SpatialTransformer layers)集成到我们的U-Net架构中。

使用Spatial Transformer编码U-Net架构

我们将使用在上一步中创建的注意力层来编码我们的U-Net架构。

class UNet_Tranformer(nn.Module):
    """A time-dependent score-based model built upon U-Net architecture."""
    def __init__(self, marginal_prob_std, channels=[32, 64, 128, 256], embed_dim=256,
                 text_dim=256, nClass=10):
        """
        Initialize a time-dependent score-based network.
        Parameters:
        - marginal_prob_std: A function that takes time t and gives the standard deviation
          of the perturbation kernel p_{0t}(x(t) | x(0)).
        - channels: The number of channels for feature maps of each resolution.
        - embed_dim: The dimensionality of Gaussian random feature embeddings of time.
        - text_dim: The embedding dimension of text/digits.
        - nClass: Number of classes to model.
        """
        super().__init__()
        # Gaussian random feature embedding layer for time
        self.time_embed = nn.Sequential(
            GaussianFourierProjection(embed_dim=embed_dim),
            nn.Linear(embed_dim, embed_dim)
        )
        # Encoding layers where the resolution decreases
        self.conv1 = nn.Conv2d(1, channels[0], 3, stride=1, bias=False)
        self.dense1 = Dense(embed_dim, channels[0])
        self.gnorm1 = nn.GroupNorm(4, num_channels=channels[0])
        self.conv2 = nn.Conv2d(channels[0], channels[1], 3, stride=2, bias=False)
        self.dense2 = Dense(embed_dim, channels[1])
        self.gnorm2 = nn.GroupNorm(32, num_channels=channels[1])
        self.conv3 = nn.Conv2d(channels[1], channels[2], 3, stride=2, bias=False)
        self.dense3 = Dense(embed_dim, channels[2])
        self.gnorm3 = nn.GroupNorm(32, num_channels=channels[2])
        self.attn3 = SpatialTransformer(channels[2], text_dim)
        self.conv4 = nn.Conv2d(channels[2], channels[3], 3, stride=2, bias=False)
        self.dense4 = Dense(embed_dim, channels[3])
        self.gnorm4 = nn.GroupNorm(32, num_channels=channels[3])
        self.attn4 = SpatialTransformer(channels[3], text_dim)
        # Decoding layers where the resolution increases
        self.tconv4 = nn.ConvTranspose2d(channels[3], channels[2], 3, stride=2, bias=False)
        self.dense5 = Dense(embed_dim, channels[2])
        self.tgnorm4 = nn.GroupNorm(32, num_channels=channels[2])
        self.tconv3 = nn.ConvTranspose2d(channels[2], channels[1], 3, stride=2, bias=False, output_padding=1)
        self.dense6 = Dense(embed_dim, channels[1])
        self.tgnorm3 = nn.GroupNorm(32, num_channels=channels[1])
        self.tconv2 = nn.ConvTranspose2d(channels[1], channels[0], 3, stride=2, bias=False, output_padding=1)
        self.dense7 = Dense(embed_dim, channels[0])
        self.tgnorm2 = nn.GroupNorm(32, num_channels=channels[0])
        self.tconv1 = nn.ConvTranspose2d(channels[0], 1, 3, stride=1)
        # The swish activation function
        self.act = nn.SiLU()
        self.marginal_prob_std = marginal_prob_std
        self.cond_embed = nn.Embedding(nClass, text_dim)
    def forward(self, x, t, y=None):
        """
        Forward pass of the UNet_Transformer model.
        Parameters:
        - x: Input tensor.
        - t: Time tensor.
        - y: Target tensor.
        Returns:
        - h: Output tensor after passing through the UNet_Transformer architecture.
        """
        # Obtain the Gaussian random feature embedding for t
        embed = self.act(self.time_embed(t))
        y_embed = self.cond_embed(y).unsqueeze(1)
        # Encoding path
        h1 = self.conv1(x) + self.dense1(embed)
        h1 = self.act(self.gnorm1(h1))
        h2 = self.conv2(h1) + self.dense2(embed)
        h2 = self.act(self.gnorm2(h2))
        h3 = self.conv3(h2) + self.dense3(embed)
        h3 = self.act(self.gnorm3(h3))
        h3 = self.attn3(h3, y_embed)
        h4 = self.conv4(h3) + self.dense4(embed)
        h4 = self.act(self.gnorm4(h4))
        h4 = self.attn4(h4, y_embed)
        # Decoding path
        h = self.tconv4(h4) + self.dense5(embed)
        h = self.act(self.tgnorm4(h))
        h = self.tconv3(h + h3) + self.dense6(embed)
        h = self.act(self.tgnorm3(h))
        h = self.tconv2(h + h2) + self.dense7(embed)
        h = self.act(self.tgnorm2(h))
        h = self.tconv1(h + h1)
        # Normalize output
        h = h / self.marginal_prob_std(t)[:, None, None, None]
        return h

现在我们已经实现了带有注意力层的U-Net结构，是时候更新我们的损失函数了。

更新配有去噪条件的U-Net损失函数

让我们通过在训练过程中结合y信息来更新损失函数。

def loss_fn_cond(model, x, y, marginal_prob_std, eps=1e-5):
    """The loss function for training score-based generative models with conditional information.
    Parameters:
    - model: A PyTorch model instance that represents a time-dependent score-based model.
    - x: A mini-batch of training data.
    - y: Conditional information (target tensor).
    - marginal_prob_std: A function that gives the standard deviation of the perturbation kernel.
    - eps: A tolerance value for numerical stability.
    Returns:
    - loss: The calculated loss.
    """
    # Sample time uniformly in the range [eps, 1-eps]
    random_t = torch.rand(x.shape[0], device=x.device) * (1. - eps) + eps
    # Generate random noise with the same shape as the input
    z = torch.randn_like(x)
    # Compute the standard deviation of the perturbation kernel at the sampled time
    std = marginal_prob_std(random_t)
    # Perturb the input data with the generated noise and scaled by the standard deviation
    perturbed_x = x + z * std[:, None, None, None]
    # Get the model's score for the perturbed input, considering conditional information
    score = model(perturbed_x, random_t, y=y)
    # Calculate the loss using the score and perturbation
    loss = torch.mean(torch.sum((score * std[:, None, None, None] + z)**2, dim=(1, 2, 3)))
    return loss

这个更新的损失函数用于计算带有附加条件的生成模型训练的损失。它涉及采样时间、生成噪声、扰动输入数据以及基于模型得分和扰动计算损失。

训练带有注意力层的U-Net架构

基于注意力层训练U-Net架构的优势是，一旦训练完成，我们就可以为我们的稳定扩散模型提供一个特定的数值来进行绘制。让我们开始训练过程，并使用以下超参数：100个训练周期，批量大小为1024，学习率为10e-3。训练将使用MNIST数据集进行。

# Specify whether to continue training or initialize a new model
continue_training = False # Either True or False
if not continue_training:
    
    # Initialize a new UNet with Transformer model
    score_model = torch.nn.DataParallel(UNet_Tranformer(marginal_prob_std=marginal_prob_std_fn))
    score_model = score_model.to(device)
# Set training hyperparameters
n_epochs =   100   #{'type':'integer'}
batch_size =  1024 #{'type':'integer'}
lr = 10e-4         #{'type':'number'}
# Load the MNIST dataset and create a data loader
dataset = MNIST('.', train=True, transform=transforms.ToTensor(), download=True)
data_loader = DataLoader(dataset, batch_size=batch_size, shuffle=True, num_workers=4)
# Define the optimizer and learning rate scheduler
optimizer = Adam(score_model.parameters(), lr=lr)
scheduler = LambdaLR(optimizer, lr_lambda=lambda epoch: max(0.2, 0.98 ** epoch))
# Use tqdm to display a progress bar over epochs
tqdm_epoch = trange(n_epochs)
for epoch in tqdm_epoch:
    avg_loss = 0.
    num_items = 0
    # Iterate over batches in the data loader
    for x, y in tqdm(data_loader):
        x = x.to(device)
        # Compute the loss using the conditional score-based model
        loss = loss_fn_cond(score_model, x, y, marginal_prob_std_fn)
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        avg_loss += loss.item() * x.shape[0]
        num_items += x.shape[0]
    # Adjust learning rate using the scheduler
    scheduler.step()
    lr_current = scheduler.get_last_lr()[0]
    # Print epoch information including average loss and current learning rate
    print('{} Average Loss: {:5f} lr {:.1e}'.format(epoch, avg_loss / num_items, lr_current))
    tqdm_epoch.set_description('Average Loss: {:5f}'.format(avg_loss / num_items))
    # Save the model checkpoint after each epoch of training
    torch.save(score_model.state_dict(), 'ckpt_transformer.pth')

在执行训练代码后，整个训练过程预计将在大约20分钟内完成。观察到的跨周期的平均损失为21.413，训练好的模型将以“ckpt_transformer.pth”文件名保存在当前目录。

生成图像

现在，有了通过注意力层实现的条件生成，我们可以指导我们的稳定扩散模型绘制任意数字。让我们观察它在被任务绘制数字9时的结果。

## Load the pre-trained checkpoint from disk.
# device = 'cuda' #@param ['cuda', 'cpu'] {'type':'string'}
ckpt = torch.load('ckpt_transformer.pth', map_location=device)
score_model.load_state_dict(ckpt)

########### Specify the digit for which to generate samples
###########
digit = 9 #@param {'type':'integer'}
###########
###########


# Set the batch size for generating samples
sample_batch_size = 64 #@param {'type':'integer'}
# Set the number of steps for the Euler-Maruyama sampler
num_steps = 250 #@param {'type':'integer'}
# Choose the sampler type (Euler-Maruyama, pc_sampler, ode_sampler)
sampler = Euler_Maruyama_sampler #@param ['Euler_Maruyama_sampler', 'pc_sampler', 'ode_sampler'] {'type': 'raw'}
# score_model.eval()
## Generate samples using the specified sampler.
samples = sampler(score_model,
        marginal_prob_std_fn,
        diffusion_coeff_fn,
        sample_batch_size,
        num_steps=num_steps,
        device=device,
        y=digit*torch.ones(sample_batch_size, dtype=torch.long))
## Sample visualization.
samples = samples.clamp(0.0, 1.0)
%matplotlib inline
import matplotlib.pyplot as plt
# Create a grid of samples for visualization
sample_grid = make_grid(samples, nrow=int(np.sqrt(sample_batch_size)))
# Plot the generated samples
plt.figure(figsize=(6,6))
plt.axis('off')
plt.imshow(sample_grid.permute(1, 2, 0).cpu(), vmin=0., vmax=1.)
plt.show()

这是我们稳定扩散架构生成的所有数字的可视化。