深度学习 (DL) 已经成为卷积神经网络 (CNN) 和生成人工智能 (Gen AI) 发展的游戏规则改变者。这种深度学习模型可以从多维空间数据（例如图像）中提取复杂的模式和特征，并进行预测。输入数据中的模式越复杂，模型架构就越复杂。加速模型训练收敛和增强模型推理性能的方法有很多，但 Batch Normalization 2D (BN2D) 已成为该领域的超级英雄。本文旨在展示将 BN2D 集成到 DL 架构中如何实现更快的收敛和更好的推理。

了解BN2D

BN2D是一种标准化技术，它应用于批处理的多维空间输入，例如图像，以标准化它们的维度（通道）值，使得这些批次的维度均具有0的均值和1的方差。

集成BN2D组件的主要目的是防止网络内部的协变量在输入数据的维度或通道中发生偏移。维度协变量内部偏移是由于在训练周期中对网络参数的更新导致维度数据分布的变化。例如，在一个卷积层中，N个过滤器产生N维激活作为输出。这一层为其过滤器维护权重和偏置参数，这些参数在每个训练周期中逐渐更新。

由于这些更新，一个过滤器的激活分布可能与同一卷积层中另一个过滤器的激活分布明显不同。这种分布上的差异表明一个过滤器的激活与另一个过滤器的激活相比处在一个截然不同的比例尺度上。当将这种比例尺度差异很大的维度数据输送到网络中的下一层时，因为比例尺度较大的维度的权重在梯度下降期间需要更新得更大，所以该层的可学习性受到了阻碍。

另一个可能的后果是，比例尺度较小的权重的梯度可能会消失，而比例尺度较大的权重的梯度可能会爆炸。当网络在这些学习障碍下的梯度下降在较大比例尺度的维度上振荡时，会严重妨碍学习收敛和训练稳定性。BN2D通过将维度数据比哦啊标准化到带有0均值和1标准偏差的标准比例来有效地缓解这种现象，并促进训练期间更快的收敛，减少了达到最佳性能所需的周期数。因此，通过简化网络的训练阶段，技术确保网络可以专注于学习更复杂和抽象的特征，允许从输入数据中提取更丰富的表示。

在标准做法中，BN2D实例通常在卷积后、激活层之前插入，例如ReLU，如下图中的示例DL网络所示。

图1

BN2D内部工作机制

下图展示了一批简单的多维空间数据示例，例如3通道图像，用于阐释BN2D技术的内部工作原理。

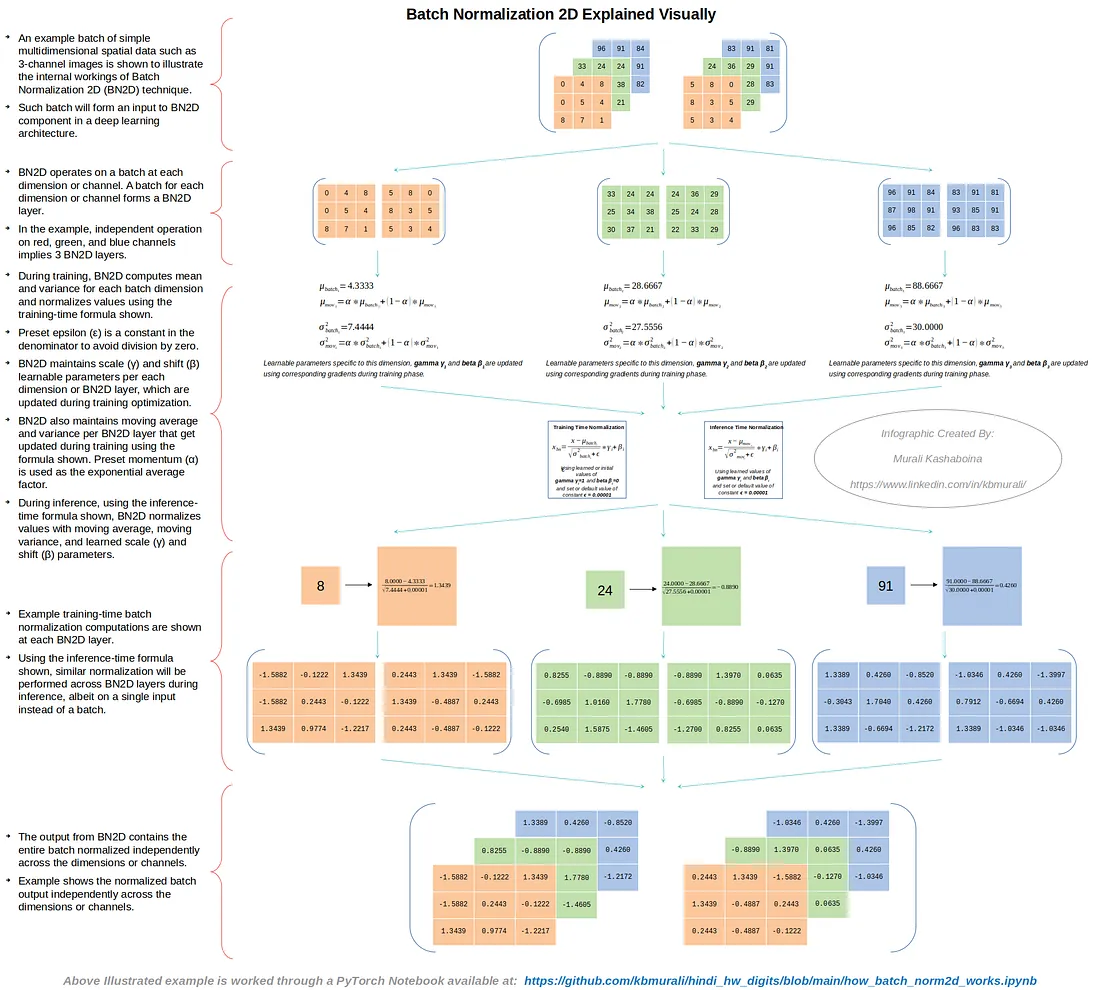
图2

如上图所示，BN2D通过在每个维度或通道处处理一个批次来实现其功能。如果一个输入批次有N个维度或通道，那么BN2D实例将具有N个BN2D层。在示例案例中，分别处理红色、绿色和蓝色通道意味着相应的BN2D实例有3个BN2D层。

图3

在训练期间，BN2D计算每个批次维度的均值和方差，并按照图2所示利用图3中展示的训练时公式对值进行比标准化。预设的epsilon (ε) 是分母中的一个常量，用来避免除以零的情况。BN2D实例为每个维度或BN2D层维护可学习的缩放（γ）和偏移（β）参数，这些参数在训练优化过程中更新。BN2D实例还维护每个BN2D层的移动平均值和方差，如图2所示，在训练中使用图3所示的公式更新。预设的动量（α）用作指数平均因子。

在推断期间，使用图3中展示的推断时公式，BN2D实例使用特定维度的移动平均值、移动方差以及学习到的缩放（γ）和偏移（β）参数对每个维度的值进行标准化。图2中展示了每个批次输入维度的训练时批量标准化计算示例。图2中的示例还展示了从BN2D实例得出的输出，其中包含独立于维度或通道的整个批次标准化的结果。

BN2D投入使用

为了检验在DL网络架构中引入BN2D实例的预期性能改进，使用了一个简单（类似玩具的）图像数据集来构建带有和不带有BN2D的相对简单的DL网络，以预测类别。预计BN2D将带来以下关键的DL模型性能改进：

1. 提高泛化能力：预计BN2D引入的标准化能提高DL模型的泛化能力。在示例中，预计引入BN2D层后，在推断时分类准确性会有所提高。
2. 更快的收敛：预计引入BN2D层有助于在训练期间加快收敛速度，减少达到最佳性能所需的训练周期数。在示例中，预计在引入BN2D层后，在早期训练丢失降低。
3. 更平滑的梯度下降：由于BN2D将维度数据标准化到均值为0和标准差为1的标准尺度上，预计可以最小化跨更大尺度维度的梯度下降的振荡，并且预计梯度下降将平稳进行。

示例数据集

使用由Kaggle发布的印地语手写数字（0-9）数据进行训练和测试具有和不具有BN2D的卷积DL模型。构建DL模型网络使用了PyTorch DL模块。选择印地语数字而不是英语数字是基于前者与后者相比的复杂性。在印地语数字中进行边缘检测比英语数字更具挑战性，因为印地语数字中的曲线比直线多。

开发了一个实用的Python函数，使得数字数据的访问更符合PyTorch数据集/数据加载器的方式，如下面的代码片段所示。训练数据集有17000个样本，而测试数据集有3000个。注意，在加载图像为PyTorch Tensors时应用了PyTorch的灰度转换器。特别开发了一个名为'ml_utils.py'的实用程序模块，用于打包运行周期、训练和测试使用PyTorch Tensor操作的深度学习模型的函数。训练和测试函数还会捕获模型指标以帮助评估模型的性能。

import torch
import torch.nn as nn
from torch.utils.data import *
import torchvision
from torchvision import transforms
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt
import seaborn as sns
from ml_utils import *
from hindi.datasets import Digits
set_seed( 5842 )
batch_size = 32
img_transformer = transforms.Compose([
                        transforms.Grayscale(),
                        transforms.ToTensor()
                    ])
train_dataset = Digits( "./data", train=True, transform=img_transformer, download=True )
test_dataset = Digits( "./data", train=False, transform=img_transformer, download=True )
train_loader = DataLoader( train_dataset, batch_size=batch_size, shuffle=True )
test_loader = DataLoader( test_dataset, batch_size=batch_size )

深度学习模型示例

第一个深度学习模型将由三个卷积层组成，每层有16个滤波器，每个滤波器的核大小为3且填充值为1，从而产生“Same”卷积。每个卷积层的激活函数是线性整流单元（ReLU）。在一个全连接层之前放置一个池化层，该池化层的池化尺寸为2，然后接一个产生10个类别输出的softmax层。该模型的网络架构如图4所示。相应的PyTorch模型定义在下面的代码片段中显示。

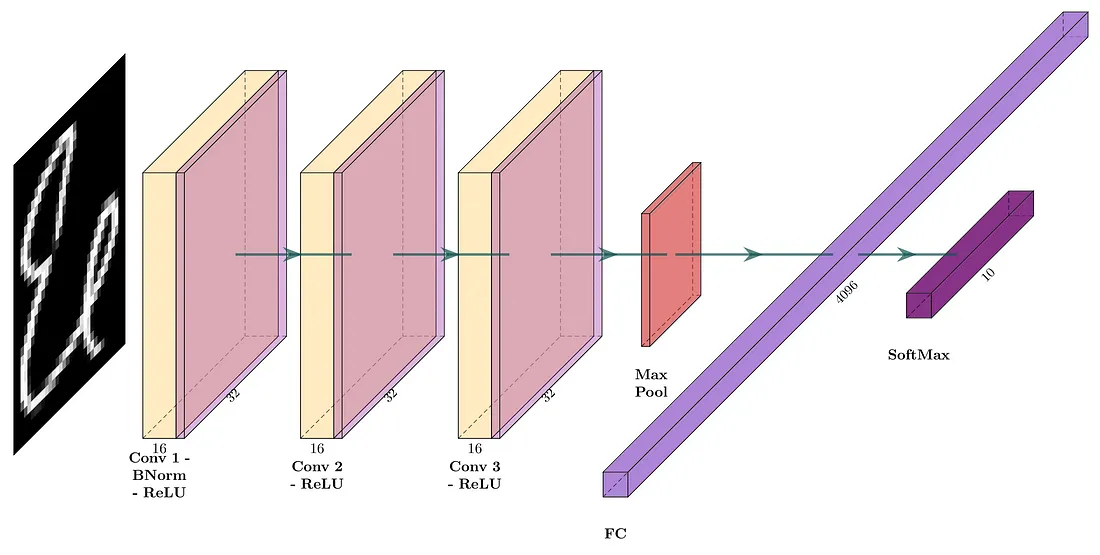
图4

device = torch.device( 'cuda' if torch.cuda.is_available() else 'cpu' )'cuda' if torch.cuda.is_available() else 'cpu' )
loss_func = nn.CrossEntropyLoss()
input_channels = 1
classes = 10
filters = 16
kernel_size = 3
padding = kernel_size//2
pool_size = 2
original_pixels_per_channel = 32*32
three_convs_model = nn.Sequential(
                                    nn.Conv2d( input_channels, filters, kernel_size, padding=padding ), # 1x32x32 => 16x32x32
                                    nn.ReLU(inplace=True), #16x32x32 => 16x32x32
                                    nn.Conv2d(filters, filters, kernel_size, padding=padding ), # 16x32x32 => 16x32x32
                                    nn.ReLU(inplace=True), #16x32x32 => 16x32x32
                                    nn.Conv2d(filters, filters, kernel_size, padding=padding ), # 16x32x32 => 16x32x32
                                    nn.ReLU(inplace=True), #16x32x32 => 16x32x32
                                    nn.MaxPool2d(pool_size), # 16x32x32 => 16x16x16
        
                                    nn.Flatten(), # 16x16x16 => 4096
                                    nn.Linear( 4096, classes) # 1024 => 10
                                )

第二个深度学习模型的结构与第一个相似，但在卷积之后和激活之前引入了2D批标准化（BN2D）实例。模型的网络架构如图5所示。相应的PyTorch模型定义在下面的代码片段中展示。

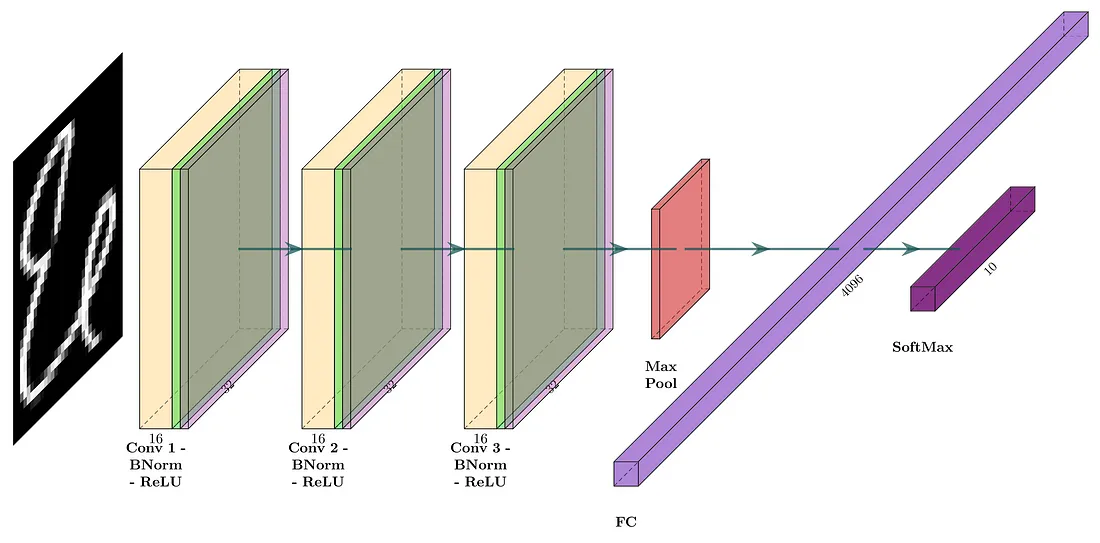
图5

three_convs_wth_bn_model = nn.Sequential(
                                            nn.Conv2d( input_channels, filters, kernel_size, padding=padding ), # 1x32x32 => 16x32x32# 1x32x32 => 16x32x32
                                            nn.BatchNorm2d( filters ), #16x32x32 => 16x32x32
                                            nn.ReLU(inplace=True), #16x32x32 => 16x32x32
                                            nn.Conv2d(filters, filters, kernel_size, padding=padding ), # 16x32x32 => 16x32x32
                                            nn.BatchNorm2d( filters ), #16x32x32 => 16x32x32
                                            nn.ReLU(inplace=True), #16x32x32 => 16x32x32
                                            nn.Conv2d(filters, filters, kernel_size, padding=padding ), # 16x32x32 => 16x32x32
                                            nn.BatchNorm2d( filters ), #16x32x32 => 16x32x32
                                            nn.ReLU(inplace=True), #16x32x32 => 16x32x32
                                            nn.MaxPool2d(pool_size), # 16x32x32 => 16x16x16
                
                                            nn.Flatten(), # 16x16x16 => 4096
                                            nn.Linear( 4096, classes) # 4096 => 10
                                       )

这两个DL模型是使用下面代码片段中显示的实用函数在示例印地语数字数据集上进行训练的。请注意，从最后一个卷积层中的滤波器的两个维度/通道捕获了两个样本权重，以便可视化训练损失的梯度下降。

three_convs_model_results_df = train_model( 
                                            three_convs_model,
                                            loss_func, 
                                            train_loader, 
                                            test_loader=test_loader, 
                                            score_funcs={'accuracy': accuracy_score}, 'accuracy': accuracy_score}, 
                                            device=device, 
                                            epochs=30,
                                            capture_conv_sample_weights=True, 
                                            conv_index=4, 
                                            wx_flt_index=3, 
                                            wx_ch_index=4, 
                                            wx_ro_index=1, 
                                            wx_index=0,
                                            wy_flt_index=3,
                                            wy_ch_index=8, 
                                            wy_ro_index=1, 
                                            wy_index=0
                                         )
three_convs_wth_bn_model_results_df = train_model( 
                                                    three_convs_wth_bn_model,
                                                    loss_func, 
                                                    train_loader, 
                                                    test_loader=test_loader, 
                                                    score_funcs={'accuracy': accuracy_score}, 
                                                    device=device, 
                                                    epochs=30,
                                                    capture_conv_sample_weights=True, 
                                                    conv_index=6, 
                                                    wx_flt_index=3, 
                                                    wx_ch_index=4, 
                                                    wx_ro_index=1, 
                                                    wx_index=0,
                                                    wy_flt_index=3,
                                                    wy_ch_index=8, 
                                                    wy_ro_index=1, 
                                                    wy_index=0
                                                 )

发现1：测试准确率提高

如图6所示，DL模型在使用BN2D实例时测试准确率更高。随着训练周期的增加，采用BN2D的模型测试准确率逐渐提高，而不使用BN2D的模型则在训练周期中准确率出现波动。在第30个周期结束时，使用BN2D的模型的测试准确率达到了99.1%，而不使用BN2D的模型仅为92.4%。这些结果表明，纳入BN2D实例对模型的性能有积极的影响，显著提高了测试准确率。

sns.lineplot( x='epoch', y='test accuracy', data=three_convs_model_results_df, label="Three Convs Without BN2D Model" )'epoch', y='test accuracy', data=three_convs_model_results_df, label="Three Convs Without BN2D Model" )
sns.lineplot( x='epoch', y='test accuracy', data=three_convs_wth_bn_model_results_df, label="Three Convs Wth BN2D Model" )

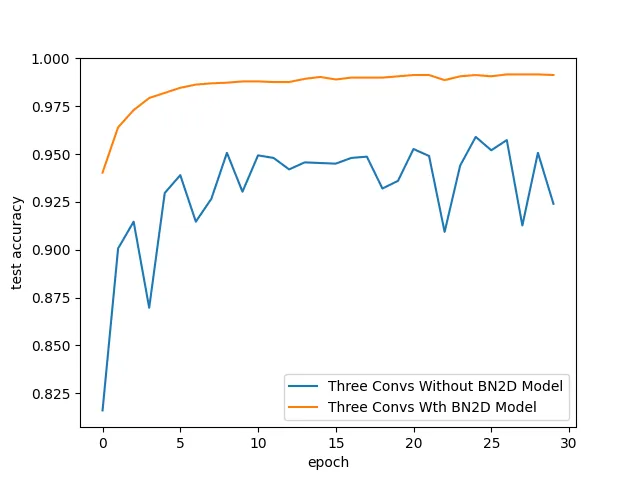
图6

发现2：更快的收敛

如图7所示，DL模型在使用BN2D实例时的训练损失显著降低。大约在第3个训练周期，使用BN2D的模型显现出的训练损失已经比不使用BN2D的情况要低。较低的训练损失表明BN2D有助于在训练期间更快速地收敛，这可能减少了达到合理收敛所需的训练周期。

sns.lineplot( x='epoch', y='train loss', data=three_convs_model_results_df, label="Three Convs Without BN2D Model" )'epoch', y='train loss', data=three_convs_model_results_df, label="Three Convs Without BN2D Model" )
sns.lineplot( x='epoch', y='train loss', data=three_convs_wth_bn_model_results_df, label="Three Convs Wth BN2D Model" )

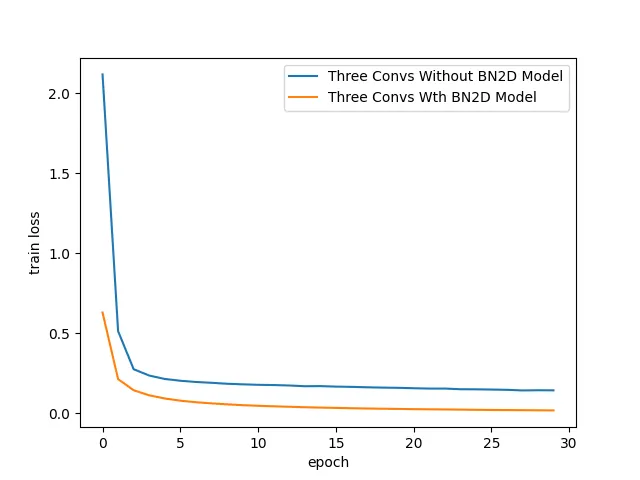
图7

发现3：平滑的梯度下降

从模型中最后一个卷积层取得的两个样本权重的损失函数，使用BN2D后表现出比没有使用BN2D时更平滑的梯度下降，正如图8所展示的。没有使用BN2D的模型损失函数遵循了相对曲折的梯度下降路径。使用BN2D后的平滑梯度下降表明，通过将维度数据标准化到以0为均值，1为标准差的标准尺度，可能使不同维度的权重能够处于相似的尺度，从而减少梯度下降的潜在振荡。

fig1 = draw_loss_descent( three_convs_model_results_df, title='Three Convs Model Without BN2D Training Loss' )'Three Convs Model Without BN2D Training Loss' )
fig2 = draw_loss_descent( three_convs_wth_bn_model_results_df, title='Three Convs With BN2D Model Training Loss' )

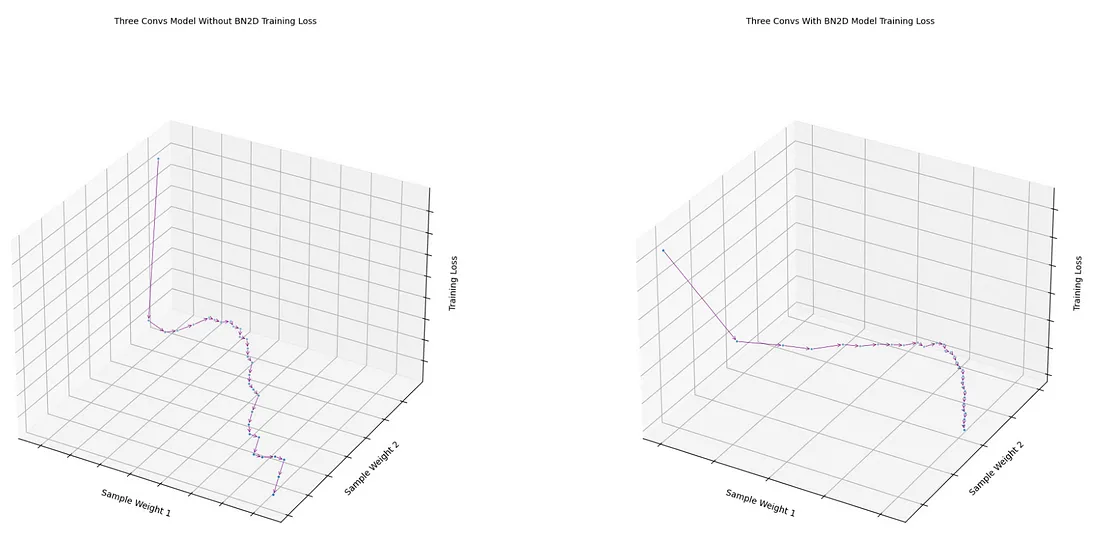
图8

虽然BN2D的好处很明显，但其实施需要仔细考虑。合适地初始化权重、选择适当的学习率以及在深度学习（DL）网络中放置BN2D层都是最大化其有效性的关键因素。尽管BN2D通常可以防止过拟合，但在某些情况下，它甚至可能导致过拟合。例如，如果BN2D与另一种称为Dropout的技术一起使用，两者的结合可能会根据具体配置和数据集对过拟合产生不同影响。同样地，对于小批量大小，批量均值和方差可能无法紧密代表整个数据集的统计特征，可能导致嘈杂的规范化，这在防止过拟合方面可能不那么有效。

结论

本文旨在展示在深度学习网络中使用BN2D的直觉。使用类似玩具的图像数据的示例卷积模型仅用于展示在DL网络架构中结合BN2D实例所期望的性能提升。BN2D在空间和通道维度上的规范化带来了训练稳定性、更快的收敛和增强的泛化能力，最终有助于深度学习模型的成功。