如果你在人工智能领域工作，梯度下降是你听到的第一个术语之一。它是用于训练模型的基础优化算法。

梯度下降的主要应用是通过调整模型参数来最小化损失函数。

梯度下降的主要应用在于训练机器学习模型。在训练过程中，模型的参数会迭代地调整，以最小化预测输出和实际目标之间的差距。梯度下降通过沿着损失函数（预测值和实际目标之间的差异）的斜率迭代移动，以达到该函数的全局最小值（以上提到的差距最小的地方）。

梯度下降是如何工作的？

数学表示 —— 步骤更新

梯度下降的数学实际上非常简单。梯度下降通过在损失的斜率方向(∇J(θ​))上取一个小“步骤”迭代更新参数（比如θ）的值。这个“步骤”的长度或值由一个名为学习率（α）的超参数决定。“步骤”的长度是α乘以斜率∇J(θ​)。

参数的新值变为旧值减去步长。

θnew​=θold​−α∇J(θold​)

其中θ代表参数，α是学习率，∇J(θ)是损失函数相对于θ的梯度。

为什么是减去？从数学上讲，当你取一个函数的梯度时，结果指向最陡增加的方向。为了往相反方向走（即最陡减少的方向），你需要减去梯度。

直观类比 —— 下山

梯度下降的基本直觉可以通过想象一个人在一个有雾的夜晚被困在山里，试图下到山谷（全局最小值）来理解。能见度极低，看不到下山的路。他们必须仅依赖于他们能看到的非常短的距离。他们可以使用梯度下降的方法，从当前所在的点向最陡坡的方向移动。 采取多个这样的步骤将导致山谷（最低点）。

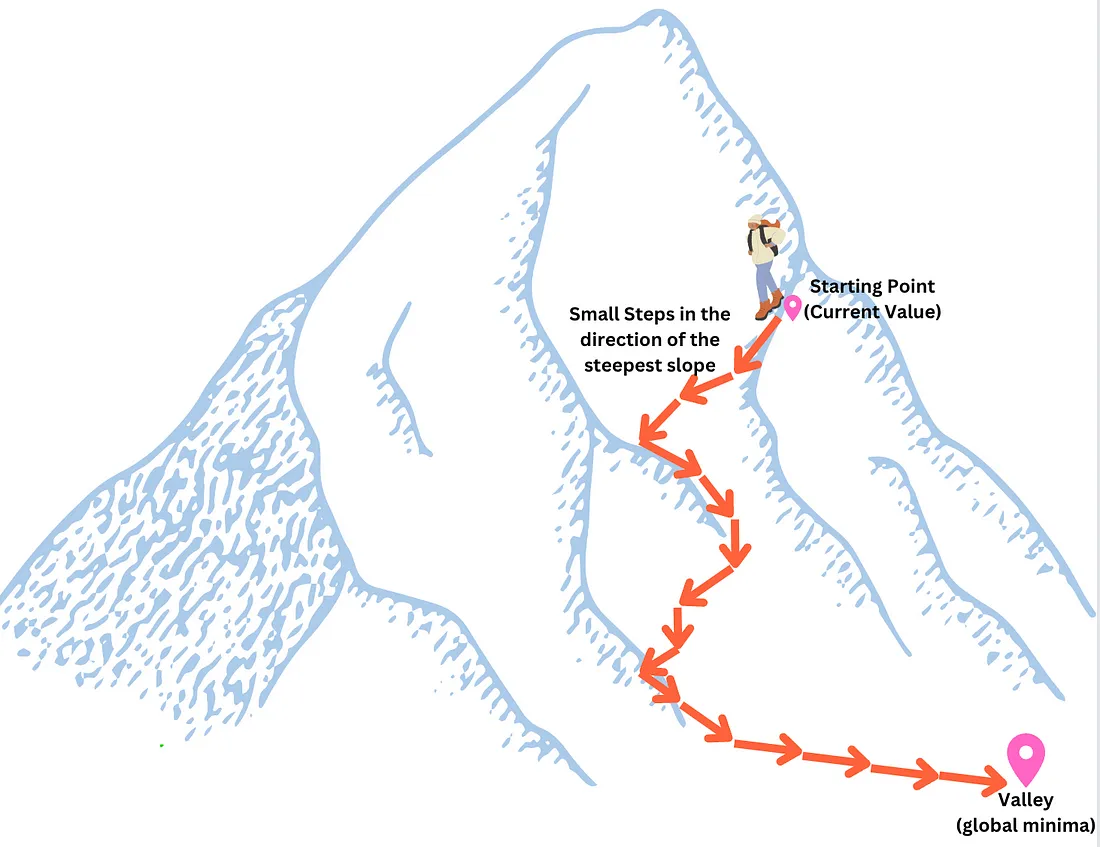
图形轮廓

以等高线图为例，每个等高线级别代表不同的损失水平。梯度下降会改变θ的值，朝着最陡峭的坡度方向进行，因此在一定数量的步骤中到达图的中心。

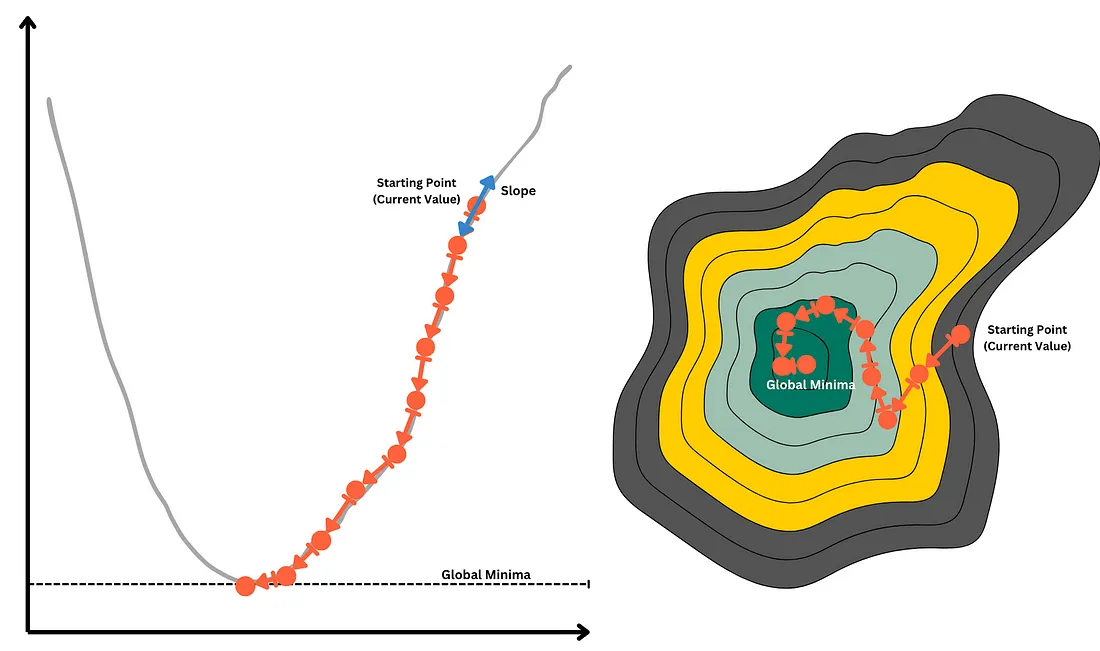
学习率 α

在梯度下降中，参数值更新步长的大小或许是最关键的因素。这个大小由一个叫做学习率（表示为 α）的超参数决定。

学习率已经成为了机器学习研究领域中最重要的超参数之一。

选择正确的学习率是机器学习的艺术。如果你设定的学习率太小，你的模型将需要非常长的时间才能收敛到最小值点。

另一方面，如果学习率过大，你可能会越过最小值点，跳到山谷的另一边。

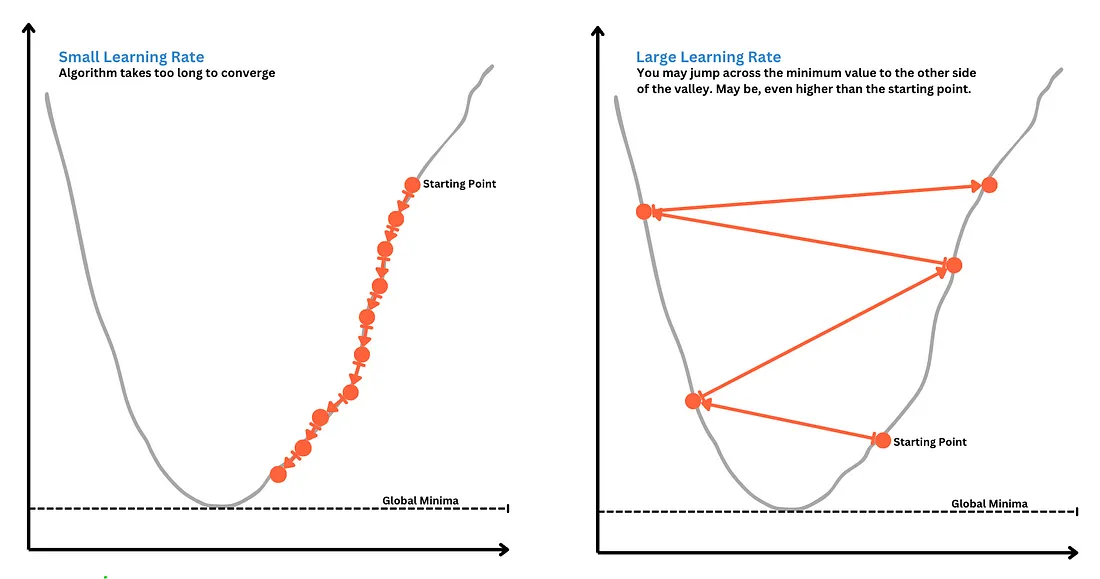
幸运的是，有各种方法可以帮助我们找到合适的学习率，例如网格搜索、学习率调度、循环学习率、自适应算法等。

全局与局部

我们一直在讨论全局最小值。然而，并非所有的损失函数都是只有一个最小值的简单凸函数。以多山地形为类比，可能会有各种不规则特征，如坑洞、高原、山脊等。如果函数遇到一个“洞”，它可能错误地认为那是最小值。另一方面，如果它遇到一个长平台，函数可能会在平台上无休止地小步行进，而永远不会到达最小值。

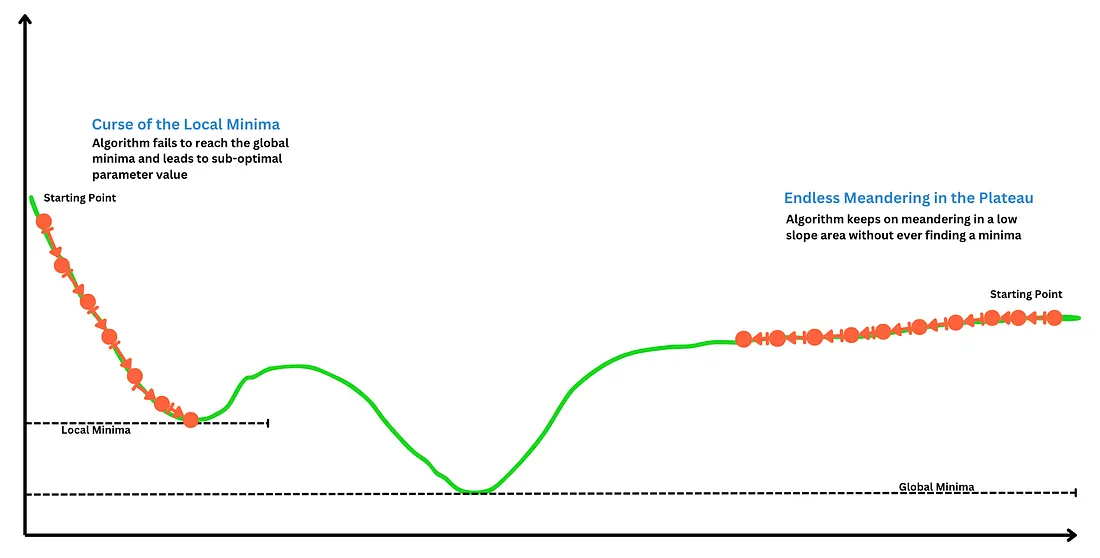
幸运的是，这些挑战在实践中并不常遇到（这一点出人意料地令人愉快），而且像均方误差这样的函数本质上是凸函数，这对梯度下降算法是有利的。

梯度下降的三种类型

梯度下降算法实现的主要计算是损失函数梯度的计算（相对于参数θ的损失函数的偏导数）。

根据训练观测数据的数量，这种计算有三种变化。

批量梯度下降（Batch Gradient Descent）

这种方法考虑使用全部训练数据（所有观测值）来计算梯度。然后，通过取数据点梯度的平均值来更新模型参数。

它简单、稳定且能保证收敛。但是，它在计算上很昂贵，而且内存密集（想象一下为计算而将所有数据存储在内存中）。

随机梯度下降（Stochastic Gradient Descent）

在本方法中，算法在每一步随机选择一个观测值来计算梯度。然后基于梯度更新参数值。

这种方法在大型数据集上很快。然而，正如我们所预期的那样，在参数更新和收敛方面有很大的变异性。

小批量梯度下降（Mini-Batch Gradient Descent）

这种方法是BGD和SGD的折中。在这种方法中，不是取全部的训练数据，而是随机选取一个小子集（一个小批次）。

它集合了BGD和SGD的最佳特性。它同样适用于并行计算，使其在处理大型数据集时高效率。仍然存在一些可变性，并且需要调整小批量的大小。

from tensorflow.keras.optimizers import SGD
sgd_optimizer = SGD(learning_rate=0.01)

深度网络优化

训练深度学习神经网络是一个缓慢的过程。存在着多重计算，每个层级都需要进行优化。权重初始化、选择合适的激活函数、归一化以及迁移学习都是加快训练进程的方法。

梯度下降是一个计算密集型算法。使用优化器加速参数值的更新，可以极大地提升训练速度。

动量：向正确方向轻推一下！

动量优化的想法是在下降过程中积累速度。在常规的梯度下降中，步长仅取决于特定点的梯度或斜率。它没有考虑前一步的斜率是怎样的。

这就像一个球沿着斜坡滚下，滚动时速度越来越快。

动量优化引入了一个动量向量‘m’，并且在每一步都从中减去斜率乘以学习率 (α∇J(θ))。

m= βm— α∇J(θ)

然后通过添加动量向量更新参数θ

θ= θ + m

一个超参数‘β’（也称为动量）控制速度，并取值在0到1之间。

使用动量优化器有两个优点：

1. 它提高了收敛速度
2. 在一些情况下，它还可以帮助克服局部最小值

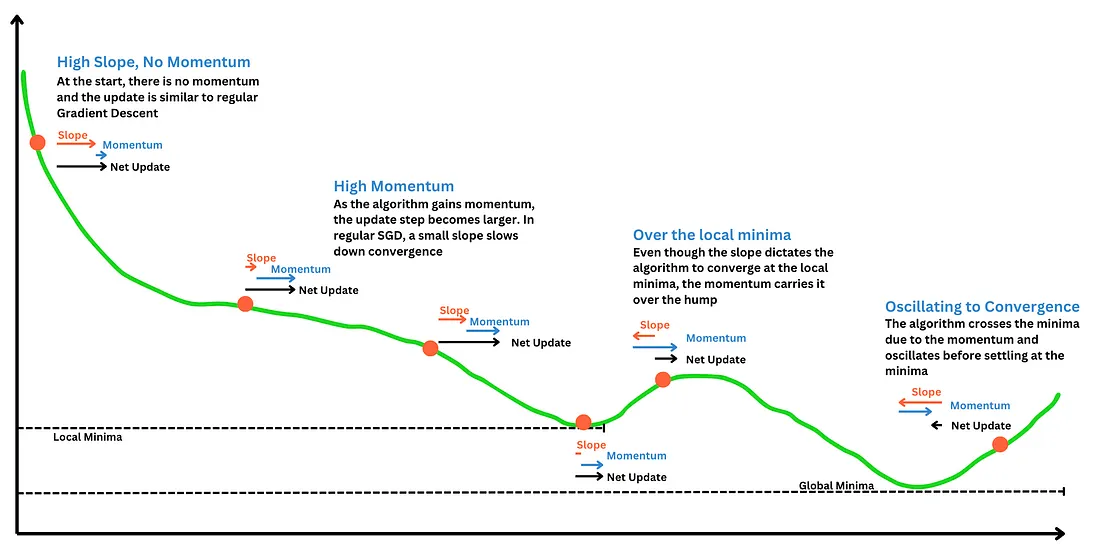
动量优化器的一个典型缺点是，该算法在停留在最小值前，会在最小值处（如球在V形谷底滚动）发生振荡。

from tensorflow.keras.optimizers import SGD
optimizer=SGD(lr=0.001, momentum=0.9)

Nesterov 加速梯度：小改变大收获

Yurii Nesterov 在 1983 年引入的 Moment Optimizer 的简单修改几乎可以保证更快的速度。Nesterov 加速梯度 (NAG)的唯一区别是，它不使用损失相对于 θ​ (∇J(θ​)) 的偏微分，而是使用整个动量向量的偏微分(∇J(θ​) +βm))

m= βm - α∇J(θ+βm)
θ = θ + m

这个小小的加项帮助更新总是更接近最优值。这有助于两个方面：

1. 它增加了收敛的速度；
2. 它减少了围绕最优值的震荡。

from tensorflow.keras.optimizers import SGD
optimizer=SGD(lr=0.001, momentum=0.9, nesterov=True)

细长谷的诅咒：在模型特征的尺度不同的情况下，损失函数会出现一个细长的谷。在这样的情况下，模型的收敛速度会下降。这是因为最陡峭的坡度并没有直接指向最优解。

AdaGrad：适应以提速

AdaGrad 算法通过将更新步骤略微指向全局最小值来解决细长谷的问题。它通过沿着最陡的维度缩小梯度来实现这一点。

它首先累积梯度的平方

s = s + square(∇J(θ)) 或 s = s + ∇J(θ) ⦻ ∇J(θ)
⦻ 表示元素间相乘

在更新步骤中，梯度通过√(s+ε)（ε 是一个平滑项）的因子被缩小（元素间除法）

θ = θ - α∇J(θ) 除以 √(s+ε)
这里的除法是元素间的

从某种程度上说，该算法使学习速率衰减——对于陡峭的斜率更快，对于缓和的斜率更慢。因此，它帮助将结果指向全局最小值。

这种衰减的学习速率被称为自适应学习速率。

AdaGrad 适合简单问题，如回归，但对于神经网络来说它停止得太早，因为学习速率被缩小了。

from tensorflow.keras.optimizers import Adagrad
optimizer=Adagrad(learning_rate=0.01)

RMSProp：每次下降都是平稳之旅

为了解决AdaGrad的问题（即学习速率降低导致收敛速度变慢），RMSProp通过只累积最近迭代的梯度来修改算法。它通过引入一个超参数ρ来实现，该参数引入了指数衰减。

s = ρs + (1-ρ)∇J(θ) ⦻ ∇J(θ)
⦻表示元素级乘法

第二步保持不变

θ = θ - α∇J(θ) 除以 √(s+ε)
这里的除法是元素级的。

from tensorflow.keras.optimizers import RMSprop
optimizer=RMSprop(learning_rate=0.01)

Adam 

Adam 或自适应矩估计 结合了 Momentum Optimizer 和 RMSProp 的优点。它跟踪过去梯度的指数衰减平均值和过去平方梯度的指数衰减平均值。

m=β*m — (1-β)∇J(θ​)
s = ρ*s + (1-ρ)∇J(θ​) ⦻ ∇J(θ​)
m*=m/(1-β)
s*=s/(1-ρ)
θ​=θ​+α*m 除以 √(s+ε)
这里的除法是逐元素的

Adam 已成为优化器的选择，因为它优于所有动量和自适应优化器

Adam 还有另一个非常强大的变体。这叫那达慕。Nadam是 Adam 加上 Nesterov 技巧（∇J(θ​+βm) 而不是 ∇J(θ​)）。那达慕总体上优于亚当。

自适应方法通常可以更快地收敛到一个好的解决方案。然而，有时你也可以使用更简单的 NAG 或带有动量的 SGD 来获得更快的结果。

from tensorflow.keras.optimizers import Adam, Nadam
adam_optimizer=Adam(learning_rate=0.01)
nadam_optimizer=Nadam(learning_rate=0.01)

优化器的世界是一个活跃的研究领域。到目前为止，只有一阶导数（或雅可比矩阵）被用于优化。二阶导数（或海森矩阵）在计算上代价高昂，速度缓慢。优化器的选择可能会根据用例而变化，更可能取决于训练数据。然而，有一些迹象表明，自适应优化器在处理大型数据集和深度网络时表现得更好。