简介

在机器学习领域，特别是在神经网络训练的背景下，存在大量影响学习过程的超参数。在这些参数中，批处理大小和学习速率是关键的。尽管人们普遍误认为这两个参数是反比关系，但实际上它们之间的关系要更加微妙。本文旨在阐明这种关系，探讨这些参数如何相互作用，并影响神经网络的学习动态。

了解批量大小和学习率

在深入探讨它们的关系之前，理解每个参数的含义至关重要。批量大小指的是在模型更新的一次迭代中使用的训练样本数。它对于决定模型的泛化能力和计算效率起着至关重要的作用。另一方面，学习率决定了优化过程中的步长，影响训练过程的收敛速度和稳定性。

在训练机器学习模型（尤其是神经网络）的背景下，批量大小和学习率之间的关系并不是直接相反的。然而，有几个关键点需要考虑：

1. 批量大小：这指的是在模型训练的一次迭代中使用的训练示例数量。更大的批量大小意味着模型将被更新得更少（每个周期的更新次数更少），但每次更新可能因为基于更多数据而更准确。较小的批量大小导致更新更频繁，潜在的方差更高，因为每次更新都是基于较少的数据。
2. 学习率：这是一个超参数，决定了优化过程中步长的大小。较高的学习率可以导致更快的收敛，但可能越过最小值，而较低的学习率确保了更谨慎的步骤，但可能花更长时间收敛或卡在局部最小值中。

批量大小和学习率之间的交互是复杂的：

• 不是直接反比关系：增加批量大小并不直接意味着应该减小学习率，反之亦然。最佳学习率通常取决于特定的数据集和模型架构，而不仅仅是批量大小。
• 稳定性和收敛性：较大的批量大小有时可以允许更大的学习率，因为梯度估计较少噪声。然而，这并不总是成立的，并且取决于训练地形的具体特点。
• 学习率调度：在实践中，学习率往往不是恒定的。学习率调度或自适应学习率方法（如Adam）在训练中根据各种因素调整学习率，这可能包括批量大小。
• 研究和启发式规则：有研究和启发式规则建议基于批量大小调整学习率的不同方式。例如，一些从业者使用“线性缩放规则”，其中学习率按新批量大小与基础批量大小的比例进行缩放。

总之，尽管批量大小和学习率之间有交互作用，它并不是一个简单的反比关系。这些参数的最佳配置可以基于模型和数据的具体上下文显著不同。

反比关系的神话

增加批量大小必然需要减小学习率，或者反过来的简化观点，在审查下并不成立。尽管较大批量大小提供更准确的梯度估计，从而可能允许更高的学习率，这不是一个规则，而是一个取决于模型和数据具体情况的可能性。

批量大小对学习动态的影响

较大的批量大小意味着每个周期更少的更新，这可能导致更稳定但潜在较慢的收敛。相反，较小的批次导致更频繁的更新，引入的噪声可以帮助逃离局部最小值，但也有不稳定训练的风险。

学习率：平衡法

学习率是确保有效收敛的关键因素。较高的学习率可以加速收敛，但风险超调，而较低的速率确保稳定但可能会放慢进程。关键是找到一个补充所选批量大小的平衡点，同时考虑到具体的训练环境。

实证观察和理论见解

经验研究已经显示出不同的结果。例如，“线性缩放规则”建议根据批量大小调整学习率。然而，并非普遍适用。理论洞察也表明，小批量引入的噪声对于寻找更平坦的最小值是有益的，这对泛化是可取的。

自适应学习率和调度

在实践中，使用自适应学习率方法（如Adam）和学习率调度（如学习率衰减）可以根据训练进度动态调整学习率，这在某种程度上独立于批量大小。这些技术提供了管理学习率的更细致的方法。

代码

为了探索批量大小和学习率在机器学习上下文中的关系，我们可以使用Python创建一个合成数据集，用不同的批量大小和学习率组合训练一个简单的神经网络模型，然后绘制结果来观察任何趋势或模式。我们将使用流行的库，如 TensorFlow/Keras 进行建模以及 matplotlib 进行绘图。

让我们分解步骤：

1. 创建一个合成数据集：我们将使用一个简单的数据集，也许是用于回归或分类任务。
2. 定义和训练模型：我们将创建一个简单的神经网络，并用不同的批大小和学习速率组合多次训练它。
3. 绘制结果：我们将绘制损失或准确性等指标，对比不同的批量大小和学习速率组合以观察任何趋势。

我将开始编写Python代码来实现这些步骤。请记住，由于神经网络训练的随机性质，每次运行的结果可能有所不同，通常需要广泛的实验才能得出可靠的结论。让我们从创建合成数据集和设置实验的代码开始。

看来TensorFlow在当前环境中不可用，因此我们无法直接在这里运行涉及TensorFlow的代码。但是，我可以指导你完成过程，你可以在本地机器上运行代码，其中安装了TensorFlow。

以下是实验的完整Python代码：

import numpy as np
import tensorflow as tf
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense
import matplotlib.pyplot as plt
# Creating a synthetic dataset for a simple regression problem
np.random.seed(0)
X = np.random.rand(1000, 10)
y = np.dot(X, np.random.rand(10, 1)) + np.random.rand(1000, 1)
# Defining a simple neural network model for the regression task
def create_model():
    model = Sequential([
        Dense(64, activation='relu', input_shape=(X.shape[1],)),
        Dense(32, activation='relu'),
        Dense(1)
    ])
    return model
# Training configurations
batch_sizes = [16, 32, 64, 128, 256]
learning_rates = [0.1, 0.01, 0.001, 0.0001]
epochs = 50
# Dictionary to store training results
results = {}
# Training the model with different batch sizes and learning rates
for batch_size in batch_sizes:
    for lr in learning_rates:
        # Create a new instance of the model
        model = create_model()
        
        # Compile the model with the current learning rate
        model.compile(optimizer=tf.keras.optimizers.Adam(learning_rate=lr), 
                      loss='mean_squared_error')
        
        # Train the model
        history = model.fit(X, y, epochs=epochs, batch_size=batch_size, verbose=0)
        
        # Store the training results
        results[(batch_size, lr)] = history.history['loss'][-1]
# Converting results to a more plot-friendly format
plot_data = {f'LR: {lr}': [results[(bs, lr)] for bs in batch_sizes] for lr in learning_rates}
# Plotting the results
plt.figure(figsize=(10, 6))
for lr, losses in plot_data.items():
    plt.plot(batch_sizes, losses, marker='o', label=lr)
plt.title('Effect of Batch Size and Learning Rate on Final Loss')
plt.xlabel('Batch Size')
plt.ylabel('Final Loss')
plt.xscale('log')
plt.yscale('log')
plt.legend()
plt.grid(True)
plt.show()

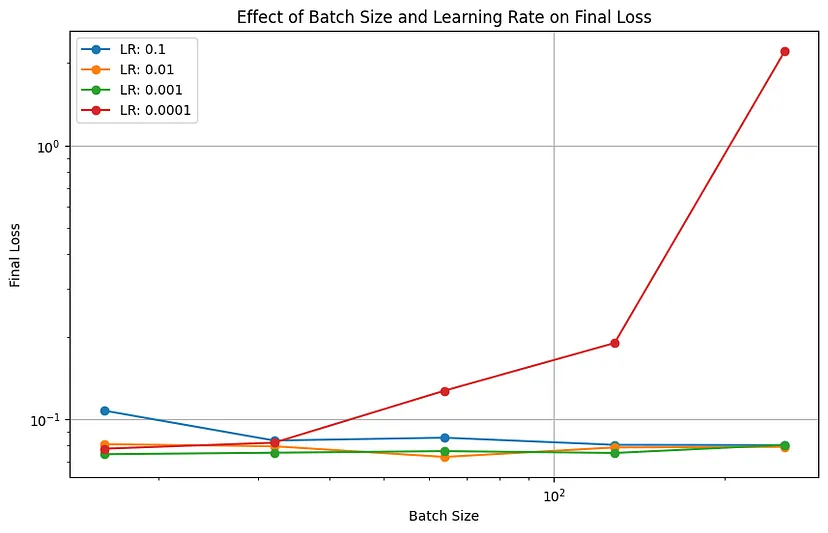
该代码将创建一个简单的神经网络，训练它在一个合成数据集上使用不同的批量大小和学习率组合，然后绘制每个组合的最终损失图。你应该会看到一个图表，x轴上是批量大小，y轴上是最终损失，不同的线代表不同的学习率。这将帮助你观察批量大小和学习率相互作用的任何模式或趋势。记住，特定的趋势可能会根据数据集和模型架构的不同而有所变化。

结论

在神经网络训练中，批量大小和学习率之间的关系是复杂的，并且依赖于上下文。它并不像通常假定的那样严格相反相关。这些参数的最佳配置取决于数据集的具体特征、模型架构以及训练目标。理解这种关系对于有效的模型训练和实现最佳性能所需的微妙平衡至关重要。需要进一步的研究和经验研究，以便在各种上下文中更好地理解这一关系。此外，能够适应性地调整这两个参数的优化算法的进步可能提供了更高效和有效神经网络训练的新途径。