简介

分层线性模型（HLM），尤其是两层分层线性模型（HLM2），是研究多层次固有结构数据的有力工具。传统的线性模型往往无法解决嵌套数据的复杂性问题，在嵌套数据中，一个层次的观测值被归类到更高层次的单元中。HLM2 具有同时分析多层次数据的能力，可以让我们对此类数据集有细致入微的了解。本文将深入探讨 HLM2 的本质，说明其结构、应用以及在不同研究领域的意义。

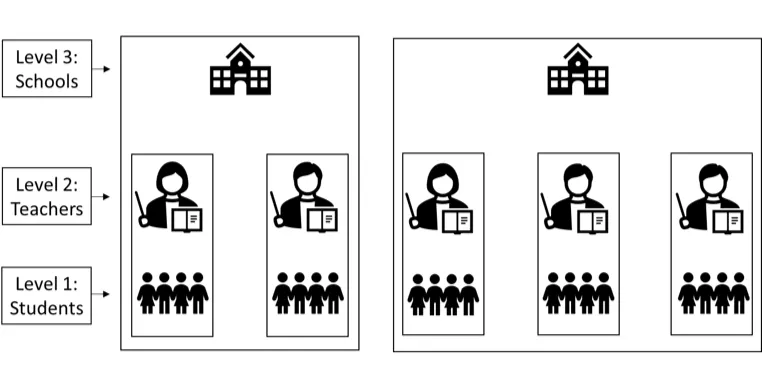
HLM2 的结构

HLM2 主要用于对个人层面数据（第 1 层）嵌套于更高层次群体（第 2 层）的数据集中的关系建模。例如，在教育研究中，学生（第 1 层）嵌套在学校（第 2 层）中。HLM2 的妙处在于它能够分别建立各层次关系的模型，从而考虑到组内潜在的相关性。第 1 层模型探讨个人层面的预测因素与结果变量之间的关系，而第 2 层模型则评估群体层面的预测因素如何影响结果。

跨领域应用

HLM2 的多功能性体现在其广泛的应用领域。在教育领域，它有助于了解学生个人属性和学校层面的政策如何影响学习成绩。在组织心理学中，可以结合个人能力和部门特点分析员工绩效。在医疗保健研究中，HLM2 可用于研究病人的治疗效果与个人健康因素和诊所层面变量的关系。这些例子都凸显了 HLM2 能够区分不同层面的预测因素的影响。

与传统模型相比的优势

HLM2 解决了传统线性模型固有的几个局限性，尤其是在处理嵌套数据时。它认识到同一群体中的个体（如同一学校的学生）并不是相互独立的，这违反了普通回归模型的基本假设。通过考虑这种组内相关性，HLM2 提供了更准确、可靠和可解释的结果。这种多层次的方法还可以同时检验固定效应（所有组间的共同效应）和随机效应（各组间的不同效应），从而提供一个全面的数据视角。

模型构建和解释挑战

构建 HLM2 需要仔细考虑数据的层次结构和指导研究的理论框架。决定在每个层次包含哪些变量以及了解它们之间的相互作用至关重要。对 HLM2 结果的解释是细致入微的，因为它涉及到对个人和群体层面的影响以及它们之间可能的相互影响的理解。此外，线性、正态和同方差假设仍然适用，因此需要进行全面的诊断检查。

软件和实施

实施 HLM2 需要专门的统计软件，如 R、Stata、SPSS 或 HLM 等专用软件。这些工具具有构建、估计和解释层次模型的功能，但需要一定的统计专业知识。

代码

在 Python 中创建一个层次线性建模 (HLM2) 的完整示例涉及几个步骤：生成合成数据集、定义层次模型、拟合模型和可视化结果。为此，我们将使用 pandas、numpy 和 statsmodels 等 Python 库。

第 1 步：生成合成数据集

让我们创建一个两级数据集。例如，假设学生（1 级）嵌套在学校（2 级）中，我们对学生个人属性（如学习时间）和学校层面因素（如学校资金）如何影响目标变量（如考试分数）感兴趣。

第 2 步：定义并拟合 HLM2

我们将使用 statsmodels 中的 MixedLM 函数定义并拟合一个两级分层线性模型。

第 3 步：可视化

我们可以使用 matplotlib 或 seaborn 等库将结果可视化。

下面让我们继续这些步骤的代码。

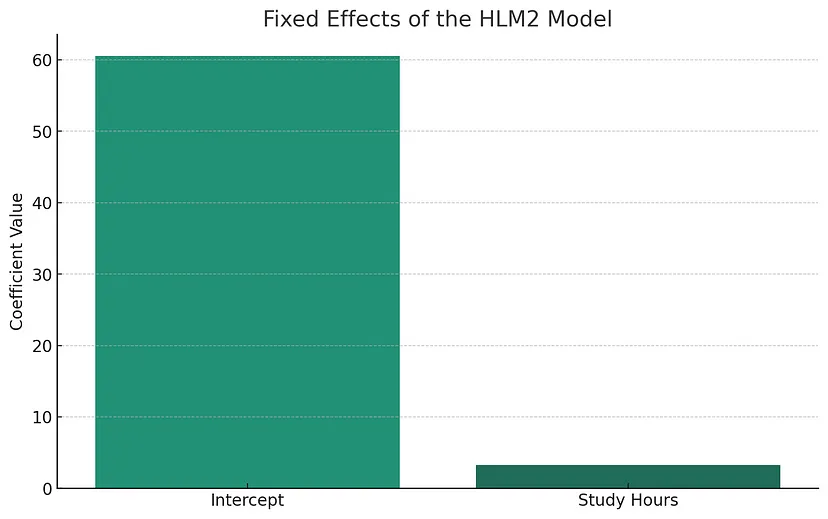
分层线性模型 (HLM2) 已成功应用于合成数据集，我们已获得结果和固定效应的可视化。

import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
import seaborn as sns
# Step 1: Generate a Synthetic Dataset
np.random.seed(42)
num_schools = 30
num_students = 300
# School-level data (Level 2)
schools = pd.DataFrame({
    "school_id": np.arange(num_schools),
    "school_funding": np.random.uniform(50000, 200000, num_schools)  # Random school funding
})
# Student-level data (Level 1)
students = pd.DataFrame({
    "student_id": np.arange(num_students),
    "school_id": np.random.choice(schools['school_id'], num_students),  # Assign students to schools
    "study_hours": np.random.uniform(1, 5, num_students)  # Random study hours
})
# Generating a target variable 'test_scores' influenced by both levels
# Let's assume both study hours and school funding positively affect test scores
students = students.merge(schools, on="school_id")
students['test_scores'] = 50 + students['study_hours'] * 3 + students['school_funding'] * 0.0001 + np.random.normal(0, 5, num_students)
# Step 2: Define and Fit the HLM2
# Random intercept model with student-level and school-level predictors
md = sm.MixedLM.from_formula("test_scores ~ study_hours", groups="school_id", re_formula="~study_hours", data=students)
mdf = md.fit()
# Step 3: Visualization
# Plotting the fixed effects
plt.figure(figsize=(10, 6))
sns.barplot(x=["Intercept", "Study Hours"], y=mdf.fe_params)
plt.title('Fixed Effects of the HLM2 Model')
plt.ylabel('Coefficient Value')
plt.show()
mdf.summary(), students.head()

模型摘要：

• 固定效应：
• 截距： 当学习时间为零时，平均考试分数约为 60.528。该值受所有学校的平均办学经费影响。
• 学习时数系数： 每增加一小时的学习时间，考试分数就会增加约 3.267 分。
• 随机效应：
• 方差成分显示了不同学校截距和斜率的变化。

解释：

• 学习时数的正系数表明，学习时数与考试分数之间存在直接的正相关关系。
• 该模型考虑了学校内部和学校之间考试成绩的差异。
• 随机效应表明，学习时间对考试成绩的影响因学校而异。

可视化：

• 柱状图显示了 HLM2 模型的固定效应，表明截距和学习时间在预测考试分数方面的重要性。

数据集预览：

• 合成数据集包含学生层面的变量（student_id、study_hours）和学校层面的变量（school_id、school_funding），以及生成的因变量（test_scores）。

通过该模型和分析，我们可以深入了解个人和群体层面的因素对结果的影响。它展示了 HLM2 在分析嵌套数据结构方面的实用性，提供了比标准线性模型更细致入微的理解。

结论

HLM2 是现代研究人员处理嵌套数据时不可或缺的工具。它能够从多个层面分析数据，提供传统模型无法提供的见解。通过对现实世界数据固有的复杂性进行适当建模，HLM2 不仅提高了统计分析的准确性，还丰富了我们对各领域多方面关系的理解。随着数据变得越来越复杂，HLM2 的相关性和应用范围必将不断扩大，成为实证研究中的一种重要方法。