简介

非负矩阵分解 (NMF) 是发现复杂数据集中潜在模式的强大工具。NMF 源于线性代数，将高维数据集分解为更简单、可解释的组件，并具有非负性的独特约束。本文深入探讨了 NMF 的概念、应用和挑战，深入探讨了其在从不同数据源中提取有意义的信息方面的关键作用。

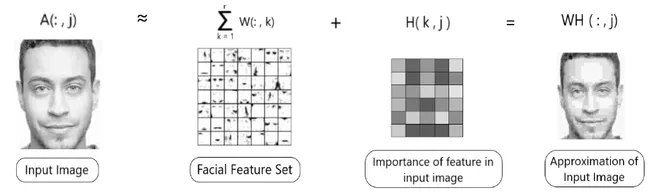
NMF概念框架

就其核心而言，NMF是一种矩阵分解技术，它将给定的非负矩阵V分解为两个低维的非负矩阵W和H。数学上，这表示为≈V≈WH，其中V是原始数据矩阵，W是基矩阵，H是系数矩阵。非负性约束是至关重要的，因为它允许数据的基于部分的表示，其中原始数据集被表示为非负特征的加法组合。

NMF的应用

1. 图像处理和计算机视觉：在这些领域中，NMF用于面部特征提取和图像分类等任务。通过将图像分解为非负矩阵，NMF分离出不同的特征（如边缘和形状），提高了模式识别和分类的准确性。
2. 文本挖掘和主题建模：NMF在自然语言处理，特别是主题建模中得到了广泛的应用。它通过识别频繁出现在一起的词组，有效地从文本文档语料库中提取主题或话题，从而能够更深入地理解文本数据的底层主题结构。
3. 生物信息学和基因组数据分析：在生物信息学中，NMF有助于识别基因表达数据的模式，帮助理解遗传途径和发现疾病的生物标志物。
4. 推荐系统：利用其处理稀疏矩阵的能力，NMF在推荐系统中用于基于过去的交互来预测用户偏好，从而提高推荐的准确性和个性化。

算法与优化

NMF的过程涉及迭代地更新矩阵W和H以最小化V和WH之间的差。用于此目的的常用算法包括交替最小二乘法（ALS）和梯度下降法。算法的选择以及W和H的初始化对非负矩阵分解的收敛性和有效性有重要影响。

挑战和限制

尽管它的多功能性，NMF面临着几个挑战。一个主要问题是等级（组件的数量）的选择，这并不简单，通常需要领域知识或启发式方法。此外，NMF可能对数据中的噪声和异常值敏感。非负性约束虽然有利于可解释性，但有时会限制NMF在数据中固有负分量的情况下的适用性。

代码

为了演示Python中的非负矩阵分解（NMF），我将为你提供完整的代码示例。该示例包括生成合成数据集，将NMF应用于该数据集，然后绘制结果以可视化分解。

合成数据集将是为本演示创建的简单矩阵。我们将使用numpy等库进行矩阵运算，使用matplotlib进行绘图。我们还将使用sklearn.decomposition来实现NMF。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.decomposition import NMF
# Generate a synthetic dataset
np.random.seed(0)
V = np.random.rand(10, 10)  # A 10x10 random matrix
# Apply NMF
model = NMF(n_components=2, init='random', random_state=0)
W = model.fit_transform(V)
H = model.components_
# Plotting
plt.figure(figsize=(15, 5))
# Original Matrix V
plt.subplot(1, 3, 1)
plt.title('Original Matrix V')
plt.imshow(V, cmap='hot', interpolation='nearest')
plt.colorbar()
# Matrix W
plt.subplot(1, 3, 2)
plt.title('Matrix W')
plt.imshow(W, cmap='hot', interpolation='nearest')
plt.colorbar()
# Matrix H
plt.subplot(1, 3, 3)
plt.title('Matrix H')
plt.imshow(H, cmap='hot', interpolation='nearest')
plt.colorbar()
plt.show()

在此代码中:

1. 我们生成一个随机的10x10矩阵V作为我们的合成数据集。
2. 我们将NMF应用于V以将其分解为矩阵W和H。为简单起见，将分量的数目（N_分量）设置为2。
3. 我们绘制原始矩阵V，以及由NMF产生的矩阵W和H。

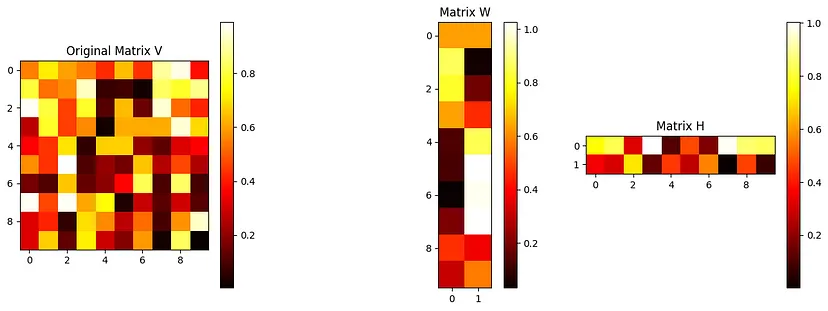
结果图将直观地演示如何将原始矩阵分解为两个矩阵的乘积，每个矩阵显示数据结构的不同方面。请记住，这是一个简单的示例；在实际应用中，NMF组件的数据和解释可能更加复杂。

结论

非负矩阵分解证明了矩阵分解技术在数据分析中的优雅和实用性。通过加强非负性，NMF提供了一种独特的方法来揭示不同数据集中隐藏的结构，使其成为各种科学和工业领域的宝贵工具。随着数据规模和复杂性的不断增长，NMF在提取有意义的模式和见解方面的作用可能会扩大，从而推动这一迷人领域的进一步创新和应用。