介绍

内核建模高斯过程（KMGPS）作为一种复杂的工具脱颖而出，旨在处理不同数据集的复杂性。它们通过强调核函数的作用扩展了高斯过程（GPS）的传统概念。本文深入研究了KMGPS的细微差别，探讨了其理论基础、实际应用以及所面临的挑战。

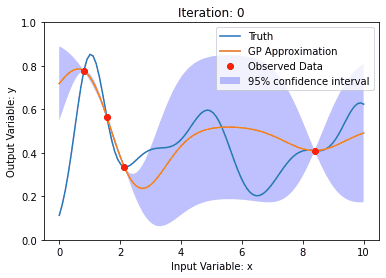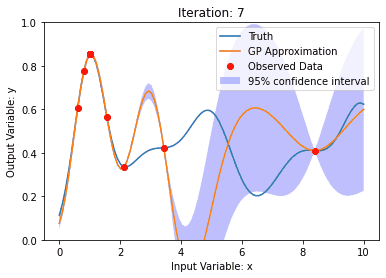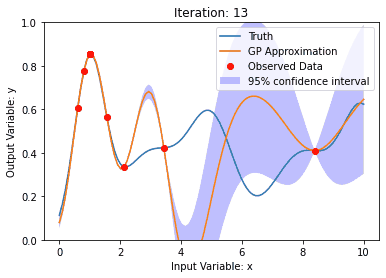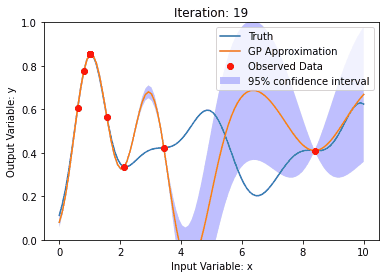
背景

核模型高斯过程（KMGPS）是机器学习和统计学中的一种方法，它扩展了传统的高斯过程（GPS）。要理解KMGPS，首先掌握高斯过程的基础知识，然后了解内核建模如何发挥作用是很有帮助的。

高斯过程（GPS）

1. 定义：高斯过程是随机变量的集合，其中任意有限数量的随机变量具有联合高斯分布。简单地说，它是一种定义函数概率分布的方法。
2. 用途：GPS通常用于机器学习中的回归和分类任务。在处理不确定性时，以及当我们需要适合我们数据的可能函数的概率分布时，它们特别有用。
3. 特点：GPS的一个关键特点是其提供不确定性估计和预测的能力。这使得它们对于理解预测中的置信度与预测本身一样重要的任务非常强大。

GPS中的核建模

1. 核函数的作用：在高斯过程中，核函数（或协方差函数）用于定义不同数据点之间的相似性。本质上，核函数接受两个输入并输出相似性得分。
2. 核函数的类型：有各种类型的核函数，如线性、多项式和径向基函数（RBF）。每个内核都有自己的特点，并根据当前的问题进行选择。
3. 内核建模：GPS中的内核建模是指选择和调整内核以最好地捕获数据中的底层模式的过程。这一点至关重要，因为内核的选择和配置会显著影响GP的性能。

核模型高斯过程（KMGPS）

1. GPS的扩展：KMGPS是标准GPS的扩展，更多地关注于核心部分。它们可能涉及为特定类型的数据或问题定制的复杂或定制设计的内核。
2. 应用：这种方法在数据复杂，标准内核不足以捕获底层关系的场景中特别有用。
3. 挑战：在KMGPS中设计和调整内核可能具有挑战性，并且通常需要在问题领域和统计建模方面的深入领域知识和专业知识。

总之，核建模高斯过程是统计学习中的一种复杂工具，为复杂数据集建模提供了一种灵活而强大的方法。它们特别有价值的是其提供不确定性估计的能力，以及通过定制内核对不同类型数据的适应性。

了解高斯过程

要理解KMGPS的本质，必须首先理解高斯过程。GPS为机器学习和统计学提供了一种概率学习方法。它们不仅仅是算法，而是用于定义和推断数据中的关系的整个框架。通过将函数视为随机变量，GPS能够在适合给定数据点集合的可能函数上进行分布，从而为回归和分类任务提供强大的工具。

核函数在GPS中的意义

GPS的核心在于其核或协方差函数。此函数用于确定数据空间中任意两点之间的关系。内核的选择极大地影响了GPS从数据中学习的能力。常见的核函数包括线性、多项式和径向基函数（RBF），每一种都有其特定的性质和应用领域。

核模型高斯过程的出现

KMGPS的出现是因为需要对数据中比标准内核所能提供的更复杂的关系进行建模。它们涉及复杂的、通常是定制设计的内核，可以捕获数据集中复杂的模式和依赖关系。

根据数据定制内核

KMGPS中内核的定制既是一门艺术，也是一门科学。它需要深入的领域知识和对统计建模的透彻理解。KMGP中设计良好的内核可以对数据中的非线性趋势、周期性和异方差（变化的噪声水平）等复杂现象进行建模。

KMGPS的应用

KMGPS的多功能性在许多领域都有应用。在地质统计学中，他们对空间数据建模，捕捉潜在的地理变化。在金融领域，它们被用来预测股票价格，解释金融市场的不稳定性和复杂性。在机器人和控制系统中，KMGPS建模并预测动态系统在不确定性下的行为。

挑战和考虑

尽管有其优势，但KMGP并非没有挑战。有效内核的设计是一项复杂的任务，通常需要反复试验和对数据的深入理解。过度拟合是一种风险，在这种情况下，模型变得过于适合训练数据，失去了对新数据的预测能力。计算复杂性是另一个问题，因为GPS通常会遇到大型数据集的可伸缩性问题。

代码

使用合成数据集和图为内核建模高斯过程（KMGPS）创建完整的Python代码示例涉及几个步骤。我们将使用像numpy这样的库进行数据操作，使用matplotlib进行绘图，使用gpy或scikit-learn进行高斯过程建模。下面是创建此类示例的分步指南：

步骤1：安装必要的库

如果你还没有安装必要的库（numpy、matplotlib和gpy或scikit-learn），你可以使用pip来安装。例如：

pip install numpy matplotlib GPy

步骤2：创建合成数据集

我们将使用NumPy创建一个合成数据集。该数据集将用于演示KMGPS的应用。

步骤3：定义并训练高斯过程模型

我们将使用GPY或Scikit-Learn来定义具有特定内核的高斯过程模型。我们可以用不同的内核进行实验，看看它们如何影响模型的性能。

步骤4：进行预测并绘制结果图

在训练模型之后，我们将使用它对测试数据集进行预测。然后，我们将把这些预测与训练数据一起绘制，以可视化模型的性能。

让我们在代码中实现它：

import numpy as np
import matplotlib.pyplot as plt
import GPy
# Step 2: Create a Synthetic Dataset
X = np.linspace(0, 10, 100)[:, None]
Y = np.sin(X) + np.random.normal(0, 0.1, X.shape)
# Step 3: Define and Train the Gaussian Process Model
# Using an RBF kernel as an example
kernel = GPy.kern.RBF(input_dim=1, variance=1., lengthscale=1.)
model = GPy.models.GPRegression(X, Y, kernel)
model.optimize(messages=True)
# Step 4: Make Predictions and Plot the Results
X_test = np.linspace(-2, 12, 200)[:, None]
Y_pred, Y_var = model.predict(X_test)
plt.figure(figsize=(10, 5))
plt.plot(X_test, Y_pred, 'r-', lw=2, label='Prediction')
plt.fill_between(X_test.flatten(), 
                 (Y_pred - 2*np.sqrt(Y_var)).flatten(), 
                 (Y_pred + 2*np.sqrt(Y_var)).flatten(), 
                 alpha=0.5, color='pink', label='Confidence Interval')
plt.scatter(X, Y, c='b', label='Training Data')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Kernel Modeled Gaussian Process Regression')
plt.legend()
plt.show()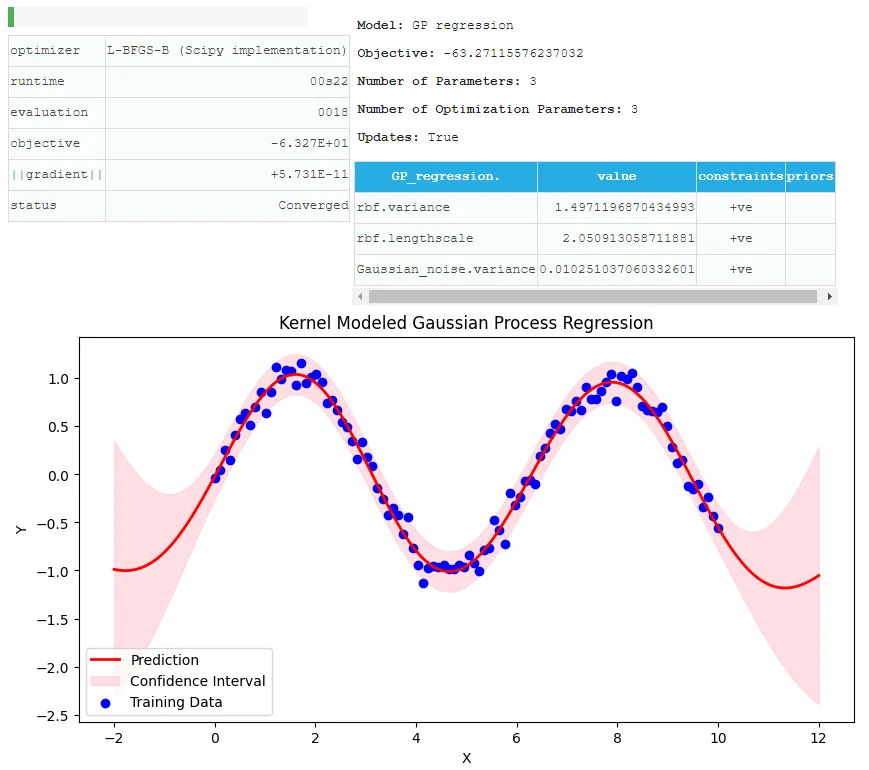

该代码将创建一个合成数据集，应用具有RBF内核的高斯过程回归模型，然后将预测与训练数据和置信区间一起绘制。你可以试验不同的内核及其参数，以了解它们如何影响模型的行为。请记住，这是一个基本示例，在实际应用程序中，内核及其参数的选择将更多地由数据驱动，并且可能涉及更复杂的决策。

结论

核模型高斯过程代表了统计学习领域的一个重大进步，为理解复杂数据集提供了一个灵活而强大的框架。通过根据数据的复杂性定制内核，KMGPS在从金融到机器人的各个领域打开了新的视野。然而，它们的有效实现需要仔细考虑内核设计和这种复杂模型所固有的挑战。随着机器学习领域的不断发展，KMGPS证明了对数据世界中不断增长的复杂性进行建模和理解的持续探索。