简介

一阶优化方法在深度学习模型的训练中举足轻重，是有效调整神经网络参数以最小化损失函数的支柱。 这些方法利用一阶导数或梯度，是模型从数据中学习并提高从图像识别到自然语言处理等任务性能的基础。 本文深入探讨了一阶优化的原理，探索了这一类别中的各种算法，并讨论了它们在深度学习中的意义。

背景

深度学习中的一阶优化方法是一种依赖于损失函数相对于模型参数的一阶导数（梯度）的优化技术。这些方法是训练深度学习模型的基础，因为它们提供了一种调整网络参数（权重和偏置）以最小化损失函数的方法。目标是提高模型在特定任务（如分类、回归或任何其他预测任务）上的性能。以下是深度学习中的一些要点和常用的一阶优化算法：

梯度下降

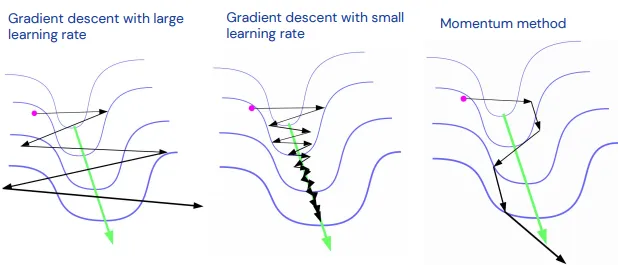
• 基本思想： 最简单的一阶优化形式，参数更新的方向与损失函数的梯度相反。这种方法采取固定大小的步骤，以达到损失函数的最小值。
• 更新规则：θ=θ-η∇θJ(θ)，其中 θ 代表参数，η 是学习率，J(θ) 是损失函数。

随机梯度下降法（SGD）

• 梯度下降法的扩展： 随机梯度下降算法不计算整个训练集的损失函数梯度（如批量梯度下降算法），而是使用基于单个或一小批示例的梯度来更新参数。这使得算法速度更快，并能处理大型数据集。
• 更新规则： 与梯度下降类似，但适用于每个实例或小批量实例。

Momentum

• 相对于 SGD 的改进：Momentum有助于加速 SGD 在相关方向上的运行，并通过将过去步骤的更新向量的一部分添加到当前步骤来抑制振荡。这种方法有助于加快收敛速度。
• 更新规则：vt=γvt-1+η∇θJ(θ)；θ=θ-vt，其中 vt 是 t 时的速度，γ 是Momentum系数。

Nesterov 加速梯度法（NAG）

• 进一步完善： NAG 是动量的一种变体，它在动量方向稍前的位置而不是当前位置计算损失函数的梯度。这种预期更新可以防止过冲，提高收敛性。
• 更新规则： 与动量类似，但采用前瞻梯度计算。

自适应梯度算法

有几种算法可以针对每个参数动态调整学习率：

• Adagrad： 根据参数调整学习率，对不经常更新的参数进行较大更新，对经常更新的参数进行较小更新。
• RMSprop： 修改 Adagrad，根据各参数梯度的近期大小调整学习率，从而提高其在非凸设置下的性能。
• Adam（自适应矩估计）： 它结合了 RMSprop 和动量的思想，为每个参数计算自适应学习率。它保留了过去梯度和梯度平方的指数衰减平均值。

主要考虑因素

• 选择正确的优化器： 优化器的选择会极大地影响训练过程的性能。这通常取决于具体任务、数据性质和神经网络的架构。
• 学习率： 神经网络训练中最关键的超参数之一。过高的学习率会导致模型发散，而过低的学习率则会导致收敛缓慢。
• 正则化和批量归一化： 正则化和批量归一化等技术虽然本身不是优化方法，但经常与优化算法一起使用，以提高训练的稳定性和性能。

一阶优化方法因其在各种情况下的简单性和有效性而被广泛使用。然而，方法及其参数（如学习率）的选择会极大地影响训练动态和最终模型性能。

一阶优化的原理

一阶优化的核心是损失函数相对于模型参数的梯度。损失函数量化了模型预测输出与实际目标值之间的差异。通过计算梯度，我们可以得到一个指向损失函数最陡峭上升方向的向量。一阶优化方法沿梯度的相反方向更新模型参数，目的是找到损失函数的局部最小值，使模型预测尽可能准确。

一阶优化的基本更新规则可表示为 θ=θ-η∇θJ(θ) ，其中 θ 代表模型参数，η 是学习率，J(θ) 是损失函数。这条规则概括了梯度下降法的精髓，是最简单、最基础的一阶优化方法。

随机梯度下降法及其变体

随机梯度下降法（SGD）对梯度下降法进行了重要修改，根据单个或小批量实例使用梯度更新参数。这种方法大大加快了优化过程，尤其是对大型数据集而言，并引入了一定程度的随机性，有助于模型摆脱局部极小值。

Momentum 和 Nesterov 加速梯度 (NAG) 是 SGD 的增强功能，解决了其对参数空间某些方向上的振荡和缓慢收敛的敏感性。通过结合随时间累积梯度的速度分量，这些方法实现了更平滑和更快的收敛。

自适应学习率方法

自适应学习率算法（如 Adagrad、RMSprop 和 Adam）可根据梯度的历史记录调整每个参数的学习率，从而进一步完善优化过程。这种自适应能力有助于处理不同参数的不同更新规模，并能带来更稳定、更高效的收敛，尤其是在复杂模型和高维空间中。

对深度学习的影响

一阶优化方法对深度学习模型的训练有若干影响。它们的高效性和可扩展性使其适用于处理深度神经网络典型的海量数据和大型参数空间。此外，自适应方法（如 Adam）的开发减少了手动调整学习率的需要，从而简化了训练过程。

不过，这些方法也并非没有挑战。学习率和批量大小等超参数的选择会极大地影响训练动态和模型性能。此外，一阶方法依赖于损失函数的平滑性和连续性，在深度学习中常见的非凸优化环境下，其有效性可能会降低。

代码

为了说明深度学习中的一阶优化，让我们用 Python 创建一个简单的示例。我们将实现一个在合成数据集上训练的基本神经网络，以解决回归问题。我们将使用随机梯度下降算法（SGD）作为优化算法，并绘制迭代时的损失图，以可视化训练过程。

让我们开始编码这些步骤。

import numpy as np
import matplotlib.pyplot as plt
# Step 1: Create a synthetic dataset
np.random.seed(42)
X = np.random.rand(100, 1)  # 100 samples, 1 feature
y = 5 * X + np.random.randn(100, 1) * 0.5 + 1  # Linear relationship with noise
# Step 2: Define the Neural Network
class SimpleNN:
    def __init__(self, input_dim, hidden_dim, output_dim):
        self.W1 = np.random.randn(input_dim, hidden_dim)
        self.b1 = np.zeros(hidden_dim)
        self.W2 = np.random.randn(hidden_dim, output_dim)
        self.b2 = np.zeros(output_dim)
    
    def forward(self, X):
        self.z1 = X.dot(self.W1) + self.b1
        self.a1 = np.tanh(self.z1)  # Activation function
        self.z2 = self.a1.dot(self.W2) + self.b2
        return self.z2
    
    def compute_loss(self, y_pred, y_true):
        return np.mean((y_pred - y_true) ** 2)
    
    def backward(self, X, y_true, y_pred, lr=0.01):
        # Gradients for W2 and b2
        dloss_dy = 2.0 * (y_pred - y_true) / y_true.size
        dy_dz2 = 1  # Derivative of linear activation
        dz2_dw2 = self.a1
        dz2_db2 = 1
        dloss_dw2 = dz2_dw2.T.dot(dloss_dy * dy_dz2)
        dloss_db2 = np.sum(dloss_dy * dy_dz2, axis=0)
        
        # Gradients for W1 and b1
        dz2_da1 = self.W2
        da1_dz1 = 1 - np.tanh(self.z1) ** 2  # Derivative of tanh
        dz1_dw1 = X
        dz1_db1 = 1
        dloss_da1 = dloss_dy.dot(dz2_da1.T)
        dloss_dz1 = dloss_da1 * da1_dz1
        dloss_dw1 = dz1_dw1.T.dot(dloss_dz1)
        dloss_db1 = np.sum(dloss_dz1, axis=0)
        
        # Update parameters
        self.W1 -= lr * dloss_dw1
        self.b1 -= lr * dloss_db1
        self.W2 -= lr * dloss_dw2
        self.b2 -= lr * dloss_db2
# Step 3: Implement SGD Optimization inside the backward method of SimpleNN class
# Step 4: Training Loop
model = SimpleNN(input_dim=1, hidden_dim=10, output_dim=1)
losses = []
epochs = 1000
for epoch in range(epochs):
    y_pred = model.forward(X)
    loss = model.compute_loss(y_pred, y)
    model.backward(X, y, y_pred)
    losses.append(loss)
    
    if epoch % 100 == 0:
        print(f'Epoch {epoch}, Loss: {loss}')
# Step 5: Plotting
plt.plot(losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Loss over Time')
plt.show()

这段代码会执行以下操作

• 生成一个具有线性关系和一些噪声的合成数据集。
• 定义一个有一个隐藏层的简单神经网络，并实施前向传播和反向传播训练。
• 使用随机梯度下降法（SGD），根据计算出的梯度更新网络权重。
• 在合成数据集上对网络进行多次历时训练，记录每次历时的损失。
• 绘制随时间变化的损失图，以直观显示训练过程和优化效果。

Epoch 0, Loss: 30.571330924788207
Epoch 100, Loss: 0.4574675521921959
Epoch 200, Loss: 0.2413588981620703
Epoch 300, Loss: 0.2272726502116684
Epoch 400, Loss: 0.22378153802601042
Epoch 500, Loss: 0.2209402657943377
Epoch 600, Loss: 0.21835485037118157
Epoch 700, Loss: 0.21600100193173397
Epoch 800, Loss: 0.21386427603989375
Epoch 900, Loss: 0.21192891045699627

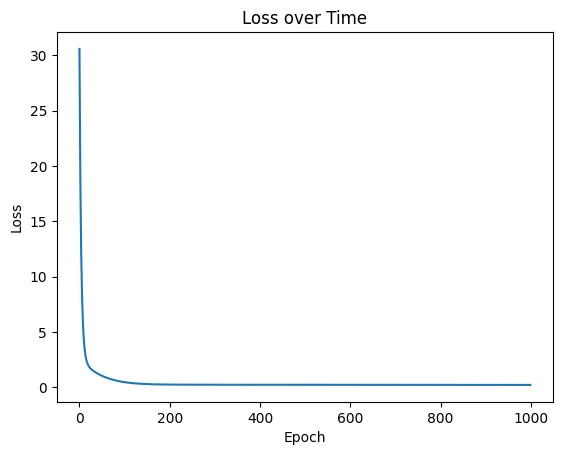
本例演示了训练深度学习模型的一阶优化基本原理。它展示了如何利用梯度迭代调整模型参数，以最小化损失函数。

结论

一阶优化方法在深度学习领域不可或缺，它在计算效率和驾驭复杂优化环境的能力之间实现了平衡。通过不断改进这些算法，深度学习模型在广泛的应用领域取得了显著的成功。随着研究的深入，优化技术的进一步发展无疑将释放模型训练和性能方面的新潜力，推动人工智能领域的下一波创新浪潮。