简介

在机器学习和人工智能快速发展的领域中，对不仅具有高精度而且能够高效运行的模型的追求是永恒的。在众多的创新中，差分进化极限学习机 (DE-ELM) 脱颖而出，成为一项重大突破，它将差分进化 (DE) 强大的优化能力与极限学习机 (ELM) 的快速学习过程融为一体。本文深入探讨了 DE-ELM 的本质，探讨其基本原理、运行机制、优势及其支持的多样化应用。

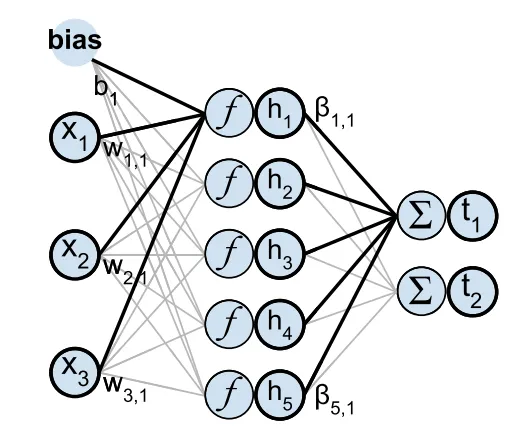
DE-ELM的基础

DE-ELM的核心在于整合两种截然不同但又互为补充的计算范式： 极限学习机和差分进化。作为前馈神经网络的基本设计，ELM 因其快速的训练过程而闻名。与所有权重和偏置都需要优化的传统神经网络不同，ELM 随机固定隐藏层的权重，只调整输出层的权重。这种独特的方法大大减少了训练时间和计算复杂度，同时保持了值得称道的泛化能力。

相反，差分进化算法是一种为连续优化问题量身定制的进化算法。它通过几代候选方案的变异和重组，以显著的效率找到全局最优方案。进化演算法的优势在于其简单性、灵活性以及在复杂的多模式景观中寻找最佳解决方案的能力。

DE-ELM的运行机制

DE-ELM 利用 DE 算法优化 ELM 的初始随机分配参数，特别是针对隐藏层的权重和偏置。通过变异、交叉和选择原则驱动的迭代调整，DE 对这些参数进行微调，以提高模型的性能。这种优化至关重要，因为它直接影响 ELM 的准确性、稳定性和泛化能力，使其成为更强大、更精确的预测工具。

DE-ELM的优势

在 DE-ELM 中，DE 和 ELM 的融合带来了无数优势。首先，它将 ELM 的高速训练与 DE 的精细优化相结合，最终形成了一个既快速又精确的模型。这种协同作用使 DE-ELM比传统模型更有效地处理复杂的问题空间，提供的解决方案不仅是最优的，而且是在极短的时间内获得的。此外，DE-ELM 还表现出显著的多功能性和鲁棒性，使其适用于从复杂的模式识别任务到不可预测环境中的预测等广泛应用。

DE-ELM的应用

DE-ELM的实际应用横跨各个领域，说明了其适应性和有效性。在生物信息学领域，它们可以分析复杂的生物数据，帮助发现遗传学和分子生物学的新见解。金融预测是 DE-ELM 的另一个优势领域，它利用 DE-ELM的预测能力来预测市场趋势和指导投资策略。环境建模、健康信息学甚至机器人学也受益于 DE-ELM的应用，它们处理大型数据集和建立非线性关系模型的能力非常宝贵。

代码

创建差分进化极限学习机（DE-ELM）的完整代码示例涉及几个步骤：生成合成数据集、定义 DE-ELM 模型、在数据集上训练模型，最后将结果可视化。本示例将引导你 Python 完成这些步骤。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
class ELM:
    def __init__(self, input_size, hidden_size, output_size):
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.input_weights = np.random.rand(input_size, hidden_size) - 0.5
        self.biases = np.random.rand(hidden_size) - 0.5
        self.output_weights = np.zeros((hidden_size, output_size))
        
    def sigmoid(self, x):
        # Clip x to avoid overflow in exp, while maintaining the sign of the input
        clip_x = np.clip(x, -500, 500)
        return 1 / (1 + np.exp(-clip_x))
    
    def fit(self, X, y):
        H = self.sigmoid(np.dot(X, self.input_weights) + self.biases)
        self.output_weights = np.dot(np.linalg.pinv(H), y)
        
    def predict(self, X):
        H = self.sigmoid(np.dot(X, self.input_weights) + self.biases)
        return np.dot(H, self.output_weights)
def de_optimize_elm(elm, X, y, pop_size=10, F=0.8, CR=0.9, generations=30):
    population = [ELM(elm.input_size, elm.hidden_size, elm.output_size) for _ in range(pop_size)]
    for generation in range(generations):
        for i in range(pop_size):
            target = population[i]
            a, b, c = np.random.choice([x for j, x in enumerate(population) if j != i], 3, replace=False)
            donor_vec = a.input_weights + F * (b.input_weights - c.input_weights)
            trial_vec = np.where(np.random.rand(*target.input_weights.shape) < CR, donor_vec, target.input_weights)
            trial_elm = ELM(elm.input_size, elm.hidden_size, elm.output_size)
            trial_elm.input_weights = trial_vec
            trial_elm.fit(X, y)
            if accuracy_score(y, trial_elm.predict(X) > 0.5) > accuracy_score(y, target.predict(X) > 0.5):
                population[i] = trial_elm
    best_elm = max(population, key=lambda elm: accuracy_score(y, elm.predict(X) > 0.5))
    elm.input_weights = best_elm.input_weights
    elm.biases = best_elm.biases
    elm.fit(X, y)
hidden_size = 50
output_size = 1  # Binary classification
elm = ELM(X_train.shape[1], hidden_size, output_size)
de_optimize_elm(elm, X_train, y_train.reshape(-1, 1))
predictions = elm.predict(X_test) > 0.5
accuracy = accuracy_score(y_test, predictions)
print(f"Accuracy: {accuracy}")
# Example plot for accuracy
plt.figure(figsize=(10, 6))
plt.plot([accuracy], label='DE-ELM Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('DE-ELM Model Accuracy')
plt.legend()
plt.show()

Accuracy: 0.7766666666666666

这个例子为 DE-ELM提供了一个基础框架。DE 优化部分，尤其是 F 和 CR 等参数的选择，以及 pop_size 和世代值，可能需要根据具体问题和数据集特征进行调整。此外，对于实际应用或更复杂的数据集，可以考虑扩展此框架，以包含更复杂的 DE 策略和 ELM 增强功能。

结论

差分进化极限学习机代表了机器学习领域的一个显著进步，体现了整合不同计算方法以实现卓越性能的力量。通过将 ELM 的快速学习速度与 DE 的优化能力相结合，DE-ELM 为解决各种复杂问题提供了一种稳健、高效和多用途的解决方案。随着人们对能够快速准确学习的智能系统的需求不断增长，DE-ELM 是计算研究创新精神的见证，推动了人工智能的发展。