介绍

异常值的存在可能会严重影响数据集的结果和解释。离群值是明显偏离其他数据的极端值，可能会产生问题，特别是当它们是由测量误差、数据输入错误或简单的自然但罕见事件造成的结果时。减轻异常值影响的一种常见技术是“winsorizing”，这是一种以统计学家 Charles P. Winsor 命名的方法。本文深入探讨了winsorizing化的概念，研究了其方法、应用、优点和潜在缺点。

背景

Winsorizing 是一种统计技术，用于尽量减少异常值对数据分析和解释的影响。它是一种通过限制极端值来转换数据的方法，以减少潜在虚假异常值的影响。具体做法是将超出一定百分位数范围的极端数据点替换为更接近中位数或平均值的值。

以下是典型的操作方法：

1. 确定百分位数： 确定数据上限的百分位数。例如，你可以选择在第 5 个和第 95 个百分位数处对数据进行Winsorizing 。
2. 替换极值： 低于下百分位数（如第 5 百分位数）的数据点会被替换为该下百分位数的值。同样，高于上百分位数（如第 95 百分位数）的数据点也会被替换为该上百分位数的值。
3. 生成数据集： 经过这样的转换后，极端值在数据集中的影响就会减小，如果这些异常值是由于测量误差或其他形式的噪音造成的，这可能是有益的。但是，如果极端值是真实的、有参考价值的，则可能不适合采用赢位法。

Winsorizing 化常用于金融分析、经济数据和其他极端值可能导致结果偏差的领域。它与修剪相关，但又不同于修剪，后者是将极端值从数据集中完全删除，而不仅仅是封顶或缩小。

这种技术假定要进行Winsorizing 化处理的数据点确实是离群值或噪声，但情况并非总是如此。因此，在应用这种方法之前，需要慎重考虑。

求和方法

Winsorizing 是一种转换技术，用于限制数据集中的极端值，以减少异常值的影响。它将低于某个下百分位数和高于某个上百分位数的数据点替换为处于这些百分位数阈值的值。例如，在 5% 胜值化中，下 5% 的数据点被设置为第 5 个百分位值，而上 5% 的数据点被设置为第 95 个百分位值。这种方法可以有效地对数据进行 "封顶"，确保极端值不会对整体分析产生不成比例的影响。

应用

在金融、经济和环境科学等多个领域都有应用，在这些领域中，异常值可能会影响分析结果。例如，在金融分析中，Winsorizing 化对于处理资产回报中的偏斜数据至关重要，因为资产回报可能会受到市场崩溃或繁荣等罕见极端事件的严重影响。在经济数据中，胜因子化有助于处理收入或财富分布中的异常值，这些异常值往往由于少数极高值而呈右偏态。

Winsorizing 的优势

Winsorizing 的主要优点是能够在不完全剔除异常值的情况下减少异常值的影响。与去除异常值的修剪法不同，Winsorizing 法保留了所有数据点，从而保留了样本量。在极端值仍与研究相关并具有信息价值的情况下，这一点尤为有益。Winsorizing 还能带来更稳健的统计估计，尤其是在非正态分布的情况下。

潜在的缺点和考虑因素

然而，Winsorizing 并非没有挑战和局限性。一个明显的缺点是选择百分位数阈值的主观性。决定使用哪个百分位数进行Winsorizing 会对结果产生重大影响，而且这种选择没有公认的标准。此外，如果极端值是基本人群的真实代表，而不仅仅是反常现象，那么Winsorizing化可能会导致估计结果出现偏差。因此，在应用这种技术之前，了解数据的性质和异常值的背景至关重要。

代码

我将提供一个完整的 Python 代码示例，使用合成数据集演示Winsorizing 。该代码将包括数据生成、数据Winsorizing 以及绘制结果以可视化Winsorizing 效果。

让我们先编写并执行这些步骤的 Python 代码。

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats.mstats import winsorize
# Step 1: Generate a Synthetic Dataset
np.random.seed(0)  # for reproducibility
data = np.random.normal(loc=50, scale=5, size=100)  # normal distribution
data = np.append(data, [100, 105, 110])  # adding outliers
# Step 2: Apply Winsorizing
winsorized_data = winsorize(data, limits=[0.05, 0.05])  # 5% winsorization at both ends
# Step 3: Plot the Results
plt.figure(figsize=(10, 6))
plt.subplot(2, 1, 1)
plt.hist(data, bins=15, alpha=0.7, label='Original Data')
plt.title('Histogram of Original Data')
plt.legend()
plt.subplot(2, 1, 2)
plt.hist(winsorized_data, bins=15, alpha=0.7, color='orange', label='Winsorized Data')
plt.title('Histogram of Winsorized Data')
plt.legend()
plt.tight_layout()
plt.show()

这段代码将生成两个直方图。第一个直方图显示原始数据集的分布情况，包括异常值；第二个直方图显示经过Winsorizing 后的分布情况，其中异常值的影响有所降低。让我们运行这段代码看看结果。

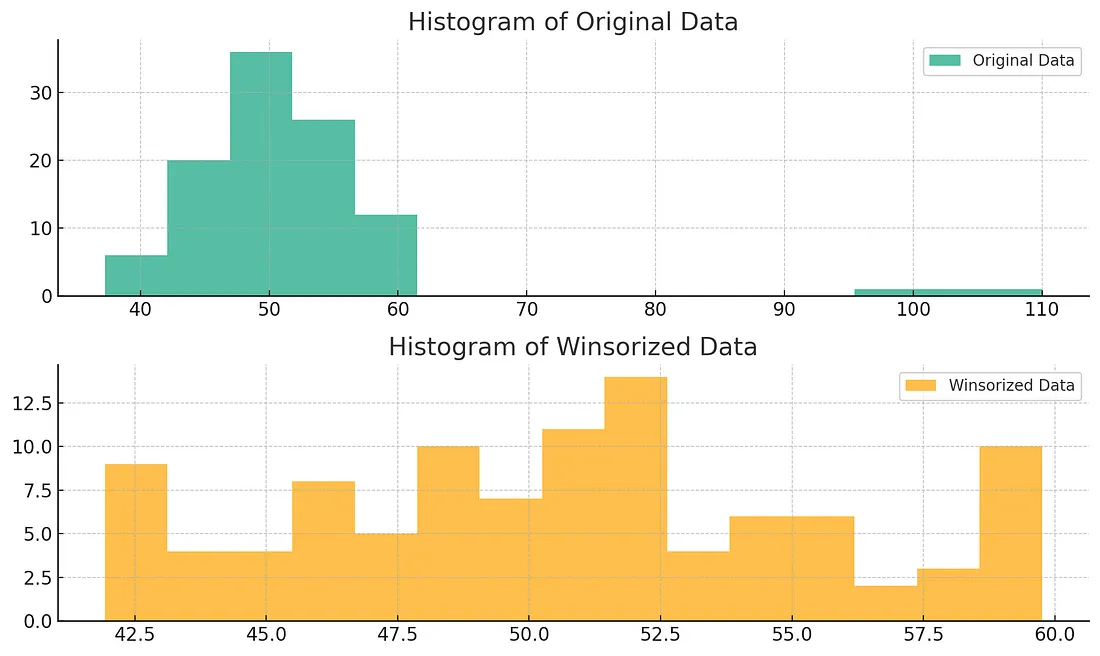
从图中可以看出，Winsorizing 有效地减少了异常值的影响，使分布更加对称。当你想保留所有数据点，同时尽量减少极端值的影响时，这种技术尤其有用。

结论

总之，winsorizing 提供了一种在数据分析中管理异常值的平衡方法。通过限制极端值的影响，可以更有代表性地了解数据的中心倾向和变异性。不过，它的有效性取决于对百分位数阈值的精心选择和对数据集特征的透彻理解。与任何统计技术一样，关键在于合理应用，确保其补充而非损害统计分析的完整性。因此，winsorizing 证明了在统计工作中处理真实世界数据的细微差别和复杂性。