简介

在数据聚类中，Gustafson-Kessel (GK) 算法是对传统方法，特别是模糊 c 均值 (FCM) 算法的显着增强。聚类是数据分析中的一项基本技术，涉及对一组对象进行分组，使得同一组中的对象彼此比其他组中的对象更相似。 GK 算法解决了 FCM 在处理非球形簇方面的局限性，提供了一种更灵活的簇形状和方向方法。本文探讨了 Gustafson-Kessel 算法的复杂性，讨论了其方法、优点以及在各个领域的应用。

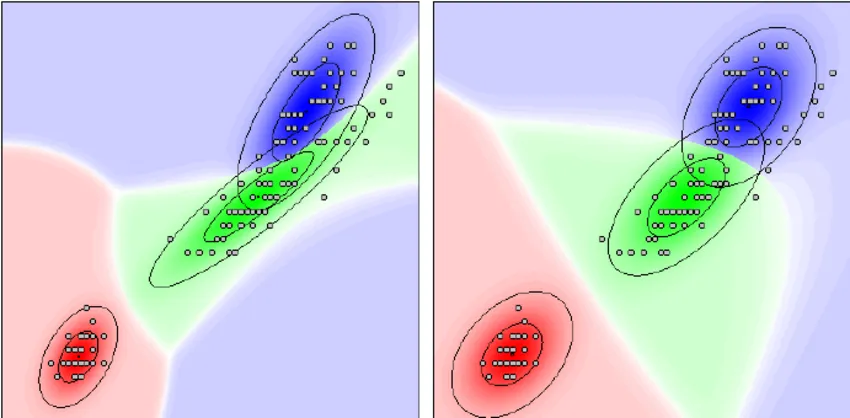
从 FCM 到 GK 的演变

模糊 c-Means 算法是聚类的基石，它的工作原理是为数据点分配与聚类相关的成员等级。然而，它的局限性在于假设聚类是球形的，而现实世界的数据并非总是如此。Gustafson 和 Kessel 开发的 Gustafson-Kessel 算法通过引入自适应距离度量来增强 FCM。该指标允许算法识别和调整椭圆形聚类，从而拓宽了模糊聚类的适用范围。

GK 算法的核心机制

GK 算法的核心是其自适应距离度量，它依赖于每个聚类的协方差矩阵。该矩阵能捕捉数据点的分布和方向，从而使算法能以椭圆方式塑造聚类。该算法迭代更新每个数据点的成员资格，并根据这些成员资格重新计算聚类中心。其目标是最小化一个考虑了模糊成员资格和自适应距离的函数，从而得到一个最佳聚类解决方案。

与传统方法相比的优势

Gustafson-Kessel 算法的主要优势在于它能灵活地适应数据的实际分布。这种适应性使其在数据集群拉长或形状各异的情况下更胜一筹。此外，GK 算法允许一个数据点隶属于多个具有不同成员资格的聚类，从而提供了更细致入微的聚类，这在复杂的数据分析场景中尤为有用。

GK 算法的应用

Gustafson-Kessel 算法的多功能性在各个领域都有应用。在图像处理中，它有助于对物体形状至关重要的图像进行分割。在模式识别中，它可以改进对非标准分布模式的分类和分析。此外，它在数据挖掘中的应用还能实现更准确的数据分类和模式发现，尤其是在结构复杂的大型数据集中。

代码

在 Python 中创建 Gustafson-Kessel 算法的完整实现以及合成数据集和图表涉及多个步骤。我将引导你完成整个过程：

1. 创建合成数据集： 我们将使用 NumPy 和 Scikit-learn 等库来生成适合演示 Gustafson-Kessel 算法的合成数据集。
2. 实现Gustafson-Kessel算法： 我们将编写 Gustafson-Kessel 算法的 Python 代码，其中包括计算自适应距离度量以及迭代更新聚类中心和成员。
3. 可视化： 我们将使用 Matplotlib 或 Seaborn 绘制结果图，展示算法如何对合成数据集进行聚类。

让我们先生成一个合成数据集，然后继续实施和可视化。我们将创建一个非球形聚类的数据集，以展示 Gustafson-Kessel 算法相对于 FCM 等传统方法的优势。

首先，让我们生成合成数据集。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
# Generate a synthetic dataset
X, _ = make_classification(n_samples=300, n_features=2, n_informative=2, n_redundant=0, 
                           n_clusters_per_class=1, class_sep=2.0, random_state=42)
# Plotting the synthetic dataset
plt.scatter(X[:, 0], X[:, 1], marker='o', s=25, edgecolor='k')
plt.title("Synthetic Dataset")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

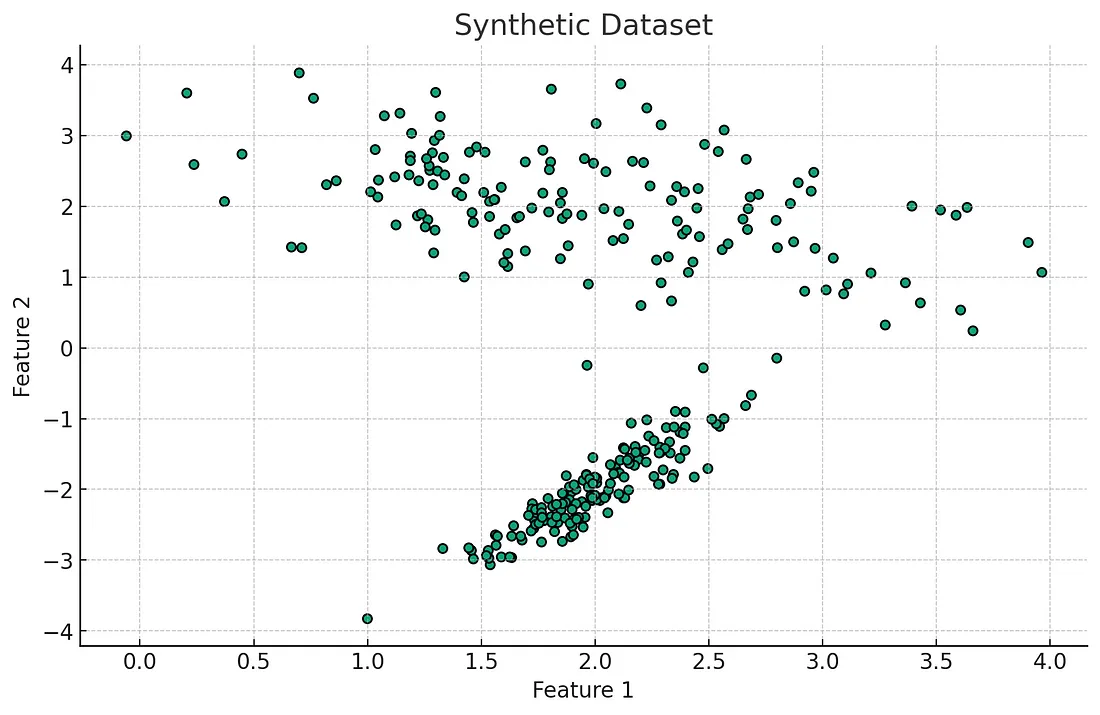
如上图所示，合成数据集由两个不同的聚类组成。现在，让我们来看看 Gustafson-Kessel 算法的实现。由于采用了自适应距离度量和模糊逻辑，该算法比基本的聚类算法更加复杂。

要实现这一功能，需要仔细处理矩阵运算并了解模糊逻辑原理。下面我们开始对该算法进行编码。请注意，由于算法的复杂性，实现过程可能会有些冗长，需要进行微调以获得最佳性能。

from numpy.linalg import inv, det
def initialize_membership_matrix(n_samples, n_clusters):
    """
    Initialize the fuzzy membership matrix.
    """
    membership_mat = np.random.random((n_samples, n_clusters))
    membership_mat /= np.sum(membership_mat, axis=1, keepdims=True)
    return membership_mat
def calculate_cluster_center(X, membership_mat, m):
    """
    Calculate cluster centers.
    """
    n_clusters = membership_mat.shape[1]
    centers = np.zeros((n_clusters, X.shape[1]))
    for i in range(n_clusters):
        num = np.sum((membership_mat[:, i, np.newaxis] ** m) * X, axis=0)
        den = np.sum(membership_mat[:, i] ** m)
        centers[i, :] = num / den
    return centers
def update_membership_matrix(X, centers, m):
    """
    Update the membership matrix.
    """
    n_samples = X.shape[0]
    n_clusters = centers.shape[0]
    new_membership_mat = np.zeros((n_samples, n_clusters))
    for i in range(n_samples):
        for j in range(n_clusters):
            sum_term = 0
            for k in range(n_clusters):
                num = np.linalg.norm(X[i, :] - centers[j, :])
                den = np.linalg.norm(X[i, :] - centers[k, :])
                sum_term += (num / den) ** (2 / (m - 1))
            new_membership_mat[i, j] = 1 / sum_term
    return new_membership_mat
def compute_covariance_matrix(X, centers, membership_mat, m):
    """
    Compute covariance matrix for each cluster.
    """
    n_clusters = centers.shape[0]
    cov_matrices = [np.zeros((X.shape[1], X.shape[1])) for _ in range(n_clusters)]
    for j in range(n_clusters):
        num = np.zeros((X.shape[1], X.shape[1]))
        den = np.sum(membership_mat[:, j] ** m)
        for i in range(X.shape[0]):
            diff = (X[i, :] - centers[j, :])[np.newaxis]
            num += (membership_mat[i, j] ** m) * np.dot(diff.T, diff)
        cov_matrices[j] = num / den
    return cov_matrices
def calculate_distance(X, centers, cov_matrices):
    """
    Calculate the adaptive distance.
    """
    n_samples = X.shape[0]
    n_clusters = centers.shape[0]
    distances = np.zeros((n_samples, n_clusters))
    for i in range(n_samples):
        for j in range(n_clusters):
            diff = (X[i, :] - centers[j, :])[np.newaxis]
            inv_cov = inv(cov_matrices[j])
            distances[i, j] = np.sqrt(np.dot(np.dot(diff, inv_cov), diff.T))
    return distances
def gustafson_kessel(X, n_clusters, max_iter=100, m=2.0):
    """
    Gustafson-Kessel algorithm.
    """
    # Initialize membership matrix
    membership_mat = initialize_membership_matrix(X.shape[0], n_clusters)
    
    # Iterate
    for iteration in range(max_iter):
        centers = calculate_cluster_center(X, membership_mat, m)
        cov_matrices = compute_covariance_matrix(X, centers, membership_mat, m)
        distances = calculate_distance(X, centers, cov_matrices)
        membership_mat = update_membership_matrix(X, centers, m)
    return centers, membership_mat
# Applying the Gustafson-Kessel algorithm to the synthetic dataset
n_clusters = 2
centers, membership_mat = gustafson_kessel(X, n_clusters)
# Plotting the results
plt.scatter(X[:, 0], X[:, 1], c=np.argmax(membership_mat, axis=1))
plt.scatter(centers[:, 0], centers[:, 1], s=300, c='red', marker='*')  # Cluster centers
plt.title("Clusters identified by Gustafson-Kessel Algorithm")
plt.xlabel("Feature 1")
plt.ylabel("Feature 2")
plt.show()

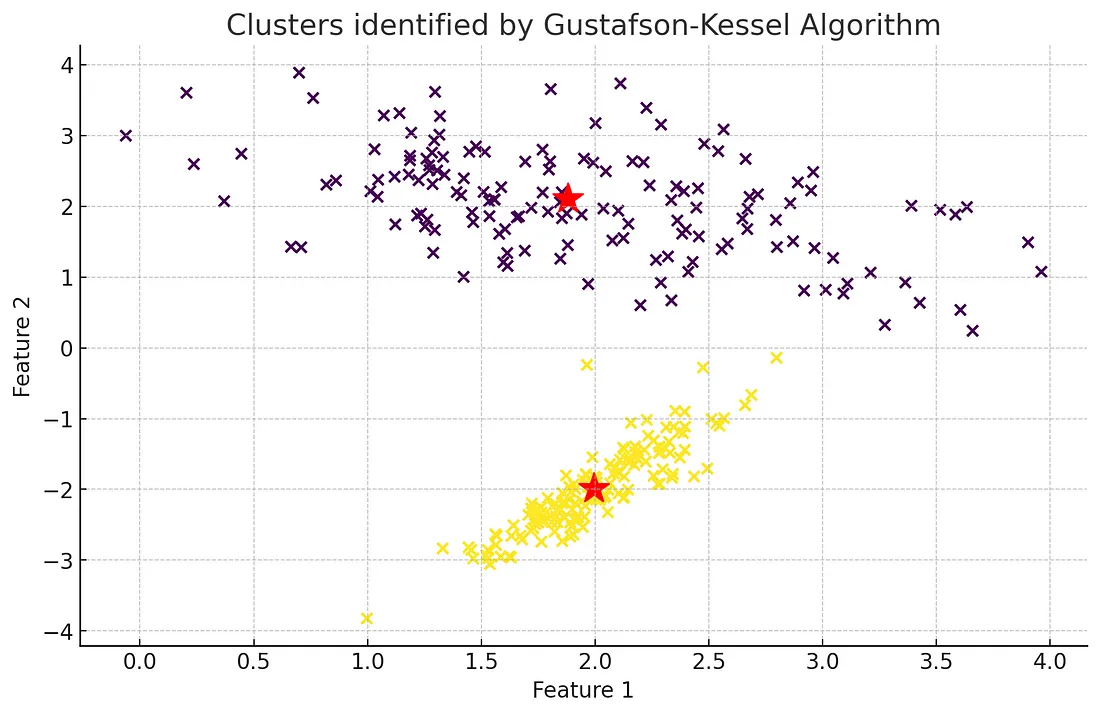
Gustafson-Kessel算法的实施已应用于合成数据集，结果如上图所示。在图中：

• 根据模糊成员值，数据点按照与之关联度最高的聚类着色。
• 红星代表计算出的聚类中心。

该可视化图展示了 Gustafson-Kessel 算法如何适应数据分布，有效识别数据集中的聚类。考虑到数据的底层结构和方向，该算法如何对数据点进行分类，从中可以看出它处理非球形聚类的能力。

请注意，此处提供的实现只是算法的基本版本。在实际应用中，可能需要进一步优化和调整，以处理更大的数据集或更复杂的情况。此外，模糊指数 m 和聚类数量等参数的选择也会对结果产生重大影响，可能需要根据数据集的具体特征进行调整。

结论

Gustafson-Kessel 算法标志着数据聚类领域的重大进步。该算法解决了模糊 c-Means 算法的局限性，并引入了聚类分析的自适应指标，为理解复杂数据集提供了一种更通用、更准确的方法。该算法在不同领域的应用凸显了它在处理现实世界数据挑战时的实用性和有效性。随着数据规模和复杂性的不断增长，像 Gustafson-Kessel 这样的算法将在从浩如烟海的信息中提取有意义的见解和模式方面发挥关键作用。