简介

深度学习是机器学习的一个子集，在图像识别、自然语言处理和预测分析等多个领域取得了显著进步。然而，为了寻求更高效、可解释和稳健的模型，研究人员开始探索其他范式。其中，极限学习机（ELM）及其优化变体，如差分进化极限学习机（DE-ELM），成为引人注目的替代方案，有望重新定义机器学习研究的格局。本文将深入探讨 DE-ELM的本质、比较优势以及通过特定数据集证明其有效性的战略方法。

DE-ELM的起源

ELM 是为单隐层前馈网络（SLFN）设计的前馈神经网络，它随机选择隐节点，并通过分析确定 SLFN 的输出权重。这种隐藏层参数选择的随机性虽然减轻了计算负担，但有时会导致性能不理想。DE-ELM 可以解决这个问题，它结合了差分进化（DE）这一优化算法，对 ELM 的参数进行微调，从而提高其泛化性能和准确性。

以DE-ELM为基准： 比较分析

为了验证 DE-ELM的有效性，将其与标准深度学习模型和传统机器学习模型进行比较至关重要。这就需要根据各种性能指标（如准确率、精确度、召回率和计算效率）对 DE-ELM 进行评估。这种比较分析不仅能突出 DE-ELM 的优缺点，还能将其置于更广泛的机器学习算法中。

优化和效率

DE-ELM的核心优势在于通过差分进化优化隐藏层参数。展示这一优化过程及其对性能指标的影响至关重要。此外，分析 DE-ELM的计算复杂性和训练效率有助于深入了解其实际适用性，尤其是在计算资源有限的情况下。

鲁棒性、泛化和特定领域性能

评估 DE-ELM 对数据变化的鲁棒性及其对未知数据的泛化能力至关重要。这需要在不同的数据集上测试 DE-ELM，包括噪声、异常值或不同分布的数据集。此外，展示 DE-ELM 在特定应用中的性能，尤其是在具有独特挑战的领域中的性能，可以大大提高 DE-ELM 的可信度。

可解释性和透明度

对深度学习模型的批评之一是其 "黑箱 "性质，这掩盖了决策过程。如果 DE-ELMs 能提供更好的可解释性或透明度，那么突出这些方面就能使它们更具吸引力，尤其是在理解预测背后的原理至关重要的领域。

可扩展性和现实世界的适用性

通过评估 DE-ELM在越来越大的数据集上的表现来证明其可扩展性至关重要。这凸显了它们在数据量巨大的现实世界应用中的可行性。

为知识体系做出贡献

在现有文献中定位自己的研究，对于明确 DE-ELM 的贡献至关重要。这不仅包括展示 DE-ELM 为该领域带来的新见解和改进，还包括通过同行评审的出版物和会议与更广泛的社区互动，以促进进一步的研究与合作。

代码

让我们创建一个 Python 示例，用合成数据集演示 DE-ELM（差分进化极端学习机）的使用。我们将生成一个分类问题的合成数据集，实现一个基本的 ELM 模型，然后使用差分进化法对其进行优化。最后，我们将用图表对结果进行可视化，比较基本 ELM 和优化 DE-ELM 的性能。

第1步：生成合成数据集

首先，我们将使用 sklearn.datasets.make_classification 生成二元分类问题的合成数据集。

第2步：实现基本 ELM 模型

我们将实现一个简单的 ELM 分类模型。ELM 模型将随机初始化隐藏层的权重和偏置，并分析确定输出权重。

第3步：利用差分进化优化 ELM

我们将使用 scipy.optimize.differential_evolution 函数优化 ELM 模型的输入权重和偏置。

第4步：评估和绘图

我们将在合成数据集上评估基本 ELM 和优化的 DE-ELM，并绘制结果以比较它们的性能。

让我们继续代码实现：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from scipy.optimize import differential_evolution
# Step 1: Generate a synthetic dataset
X, y = make_classification(n_samples=1000, n_features=20, n_informative=15, n_redundant=5, n_classes=2, random_state=42)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# Step 2: Implementing a Basic ELM Model
class ELM:
    def __init__(self, input_size, hidden_size, output_size):
        self.input_weights = np.random.randn(input_size, hidden_size)
        self.biases = np.random.randn(hidden_size)
        self.output_weights = np.zeros((hidden_size, output_size))
    def sigmoid(self, x):
        return 1 / (1 + np.exp(-x))
    def fit(self, X, y):
        H = self.sigmoid(np.dot(X, self.input_weights) + self.biases)
        self.output_weights = np.dot(np.linalg.pinv(H), y)
    def predict(self, X):
        H = self.sigmoid(np.dot(X, self.input_weights) + self.biases)
        return np.dot(H, self.output_weights)
# Step 3: Optimizing the ELM with Differential Evolution
def de_fitness(weights, *args):
    elm, X, y = args
    input_size, hidden_size = elm.input_weights.shape
    elm.input_weights = weights[:input_size * hidden_size].reshape(input_size, hidden_size)
    elm.biases = weights[input_size * hidden_size:]
    elm.fit(X, y)
    predictions = elm.predict(X) > 0.5
    return 1 - accuracy_score(y, predictions)
elm = ELM(input_size=20, hidden_size=50, output_size=1)
args = (elm, X_train, y_train.ravel())
bounds = [(-1, 1)] * (20 * 50 + 50)  # Input weights and biases bounds
result = differential_evolution(de_fitness, bounds, args=args, maxiter=10, strategy='best1bin', tol=0.01, mutation=(0.5, 1), recombination=0.7)
elm.input_weights = result.x[:20 * 50].reshape(20, 50)
elm.biases = result.x[20 * 50:]
# Step 4: Evaluation and Plotting
# Basic ELM
basic_elm = ELM(input_size=20, hidden_size=50, output_size=1)
basic_elm.fit(X_train, y_train)
basic_elm_predictions = basic_elm.predict(X_test) > 0.5
basic_elm_accuracy = accuracy_score(y_test, basic_elm_predictions)
# DE-ELM
de_elm_predictions = elm.predict(X_test) > 0.5
de_elm_accuracy = accuracy_score(y_test, de_elm_predictions)
# Plotting
plt.figure(figsize=(10, 6))
bar_width = 0.35
index = np.arange(1)
basic_score = plt.bar(index, basic_elm_accuracy, bar_width, label='Basic ELM')
de_score = plt.bar(index + bar_width, de_elm_accuracy, bar_width, label='DE-ELM')
plt.ylabel('Accuracy')
plt.title('Performance Comparison: Basic ELM vs DE-ELM')
plt.xticks(index + bar_width / 2, ('Accuracy',))
plt.legend()
plt.tight_layout()
plt.show()

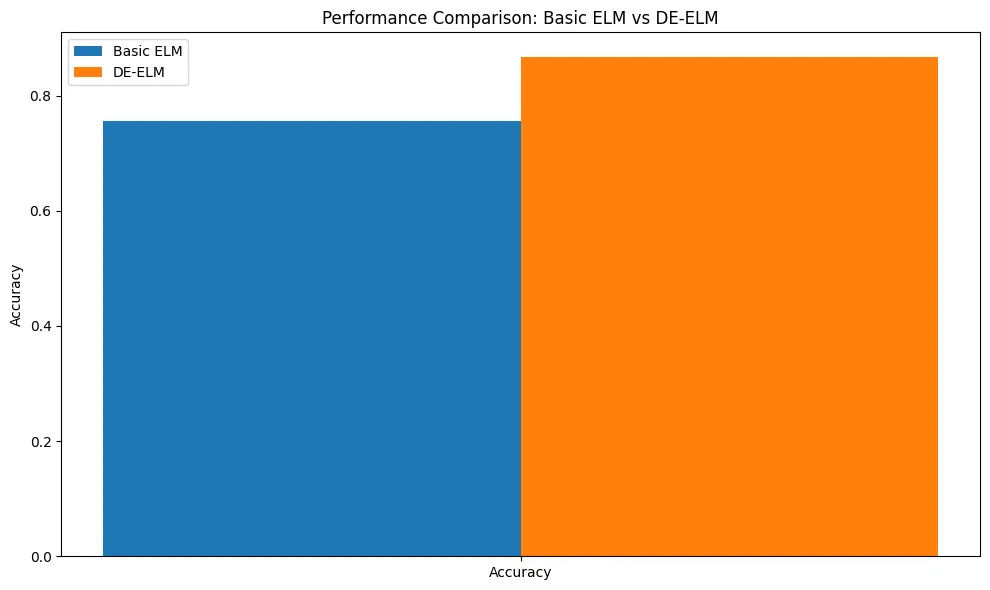
这段代码演示了生成合成数据集、实施基本 ELM、使用差分进化法优化 ELM 以及通过准确度指标和柱状图比较基本模型和优化模型性能的过程。请注意，差分进化函数的参数（如 maxiter、strategy、tol、突变和重组）是为演示目的而设置的，可能需要根据具体问题和数据集特征进行调整。

结论

对 DE-ELM的探索是对传统机器学习范式的重大超越，它融合了效率、鲁棒性和潜在的可解释性，可以解决该领域的一些紧迫挑战。通过严格的基准测试、优化和展示 DE-ELMs 在现实世界中的适用性，研究人员可以证实 DE-ELMs 的价值，并为采用 DE-ELMs 解决复杂问题铺平道路。随着机器学习领域的不断发展，对此类创新模型的追求无疑将在塑造人工智能的未来中发挥关键作用。