RAG 应用程序的最大问题之一是其计算检索时间。想象一下，你有一个包含一万亿条嵌入向量记录的向量数据库。当你尝试将用户查询与一万亿个向量进行匹配时，肯定需要一分钟多的时间才能检索到正确的信息。

我们能否使用 CPU 内核上的并行处理将检索正确信息的时间缩短至几秒？

减少时间需要找到有效的方法来计算用户查询嵌入向量与向量数据库中存储的数百万、十亿甚至万亿个其他嵌入向量之间的余弦相似度。

Chunkdot是在MIT 许可下专门为此目的而设计的，为密集矩阵和稀疏矩阵提供多线程矩阵乘法。它适合通过对项目矩阵表示（嵌入）进行分段并使用 Numba 来加速计算来计算大量项目的 K 个最相似的项目。

HuggingFace 上有许多可用的数据集，提供超过一百万个条目的嵌入向量，例如来自 Qdrant 的数据集。你可以使用它来测试 Chunkdot 性能。然而，为了进行详细的性能测量，我们将使用 NumPy 库生成各种维度的随机嵌入向量。

我们将比较两种方法，一种来自 Chunkdot，第二种是余弦相似度的伪代码。我们将观察增加尺寸和维度如何影响性能。我将使用 Kaggle（无 GPU）笔记本来完成此任务，以确保一致性。

搭建舞台

Chunkdot 需要与任何其他库类似的安装过程。

# installing chunkdot
pip install chunkdot

在运行任何程序之前，我们必须先检查 Kaggle 环境中的可用内存。

# Checking available memory
!free -h

检查可用内存对 Chunkdot 至关重要。随着向量数据库大小的增加，计算内存也在增加。为了防止超出可用内存，监控硬件的剩余内存非常重要。在我的例子中，可用空间为 25GB，不包括 Buff/Cache。

让我们导入必要的库。

# to matrix generate matrices
import numpy as np
# importing cosine similarity module from chunkdot
from chunkdot import cosine_similarity_top_k
# to calculate computation time
import timeit

编码伪代码算法

首先，我们将构建一个伪代码算法，计算用户查询向量与数据库或本地存储的其他数百万个向量之间的余弦相似度。

def cosine_pseudocode(query_v, doc_v, num_indices):
    """
    Retrieve indices of the highest cosine similarity values between
    the query vector and embeddings.
    
    Parameters:
        query_v (numpy.ndarray): Query vector.
        doc_v (list of numpy.ndarray): List of embedding vectors.
        num_indices (int): Number of Top indices to retrieve.
        
    Returns:
        list of int: Indices of the highest cosine similarity values.
    """
    cosine_similarities = []  # Initialize an empty list to store cosine similarities
    query_norm = np.linalg.norm(query_v)  # Calculate the norm of the query vector
    
    # Iterate over each documents embedding vectors in the list
    for vec in doc_v:
        dot_product = np.dot(vec, query_v.T)  # Calculate dot product between embedding vector and query vector
        embedding_norm = np.linalg.norm(vec)  # Calculate the norm of the embedding vector
        cosine_similarity = dot_product / (embedding_norm * query_norm)  # Calculate cosine similarity
        cosine_similarities.append(cosine_similarity)  # Append cosine similarity to the list
    
    cosine_similarities = np.array(cosine_similarities)  # Convert the list to a numpy array
    
    # Sort the array in descending order
    sorted_array = sorted(range(len(cosine_similarities)), key=lambda i: cosine_similarities[i], reverse=True)
    # Get indices of the top two values
    top_indices = sorted_array[:num_indices]
    
    # Return the indices of highest cosine similarity values
    return top_indices

除了 NumPy 之外，这个余弦相似度函数不依赖于任何库，它需要三个输入：

• query_v 用户查询的嵌入向量
• doc_v 某处存储的文档的嵌入向量
• num_indices：相似的 top_k 结果的文档索引号

编码 Chunkdot 算法

现在我们已经编码了伪代码算法，下一步就是编码 Chunkdot 余弦相似度函数。

def cosine_chunkdot(query_v, doc_v, num_indices, max_memory):
    """
    Calculate cosine similarity using the chunkdot library.
    
    Parameters:
        query_v (numpy.ndarray): Query vector.
        doc_v (numpy.ndarray): List of Embedding vectors.
        num_indices (int): Number of top indices to retrieve.
        max_memory (float): Maximum memory to use.
        
    Returns:
        numpy.ndarray: Top k indices.
    """
    
    # Calculate Cosine Similarity
    cosine_array = cosine_similarity_top_k(embeddings=query_v, embeddings_right=doc_v, 
                                          top_k=num_indices, max_memory=max_memory)  # Calculate cosine similarity using chunkdot
    # Get indices of the top values
    top_indices = cosine_array.nonzero()[1]
    
    # return the top similar results
    return top_indices

Chunkdot 函数有四个输入：

• query_v 用户查询的嵌入向量
• doc_v 某处存储的文档的嵌入向量
• num_indices查找相似的 top_k 结果
• max_memory 表示用于计算的可用内存，单位为字节。例如，1E9 表示 1GB，10E9 表示 10GB，以此类推。

让我们在样本数据集上测试这两个函数，观察它们的输出结果。

doc_embeddings = np.random.randn(10, 100) # 10 document embeddings (100 dim)10, 100) # 10 document embeddings (100 dim)
user_query = np.random.rand(1,100) # 1 user query (100 dim)
top_indices = 1 # number of top indices to retrieve
max_memory = 5E9 # maximum memory to use (5GB)
# retrieve indices of the highest cosine similarity values using pseudocode
print("top indices using pseudocode:", cosine_pseudocode(user_query, doc_embeddings, top_indices))
# retrieve indices of the highest cosine similarity values using chunkdot
print("top indices using chunkdot:", cosine_chunkdot(user_query, doc_embeddings, top_indices, max_memory))

### OUTPUT ###
top indices using pseudocode: [4]
top indices using chunkdot: [4]
### OUTPUT ###

我随机生成了 10 个文档嵌入向量（每个向量的维数为 100）和一个用户查询，用户查询是具有相同维数的单个嵌入向量。top_indices 参数设置为 1，这意味着它将根据最高余弦相似度从文档嵌入向量中只返回一个相似项的索引。内存使用量设置为 5E9，相当于 5GB。我们的两个函数都返回相同的索引，即 4，这表明我们对两个函数都进行了精确编码。

编码计算时间函数

我们还需要创建一个计时函数，用于测量这两个函数输出结果所需的计算时间。

# calculate time taken
def calculate_execution_time(query_v, doc_v, num_indices, max_memory, times):
    
    # calculate time taken to execute the pseudocode function
    pseudocode_time = round(timeit.timeit(lambda: cosine_pseudocode(query_v, doc_v, num_indices), number=times), 5)
    # calculate time taken to execute the chunkdot function
    chunkdot_time = round(timeit.timeit(lambda: cosine_chunkdot(query_v, doc_v, num_indices, max_memory), number=times), 5)
    # print the time taken
    print("Time taken for pseudocode function:", pseudocode_time, "seconds")
    print("Time taken for chunkdot function:", chunkdot_time, "seconds")

测试 10k 个向量嵌入

我们将从合理的文档嵌入数量（10000）开始，这与小规模的特定领域 RAG 应用程序相当。我将每个嵌入向量的维度设置为 1536，这相当于 OpenAI 的嵌入模型 text-embedding-3-small。

让我们通过运行 100 次来计算每种方法的计算时间。

doc_embeddings = np.random.randn(10000, 1536) # 10K document embeddings (1536 dim)10000, 1536) # 10K document embeddings (1536 dim)
user_query = np.random.rand(1,1536) # user query (1536 dim)
top_indices = 1 # number of top indices to retrieve 
max_memory = 5E9 # maximum memory set to 5GB
# compute the time taken to execute the functions
calculate_execution_time(user_query, doc_embeddings, top_indices, max_memory, 100)

对于 10k 文档嵌入，维度为 1536，运行两种算法 100 次，对比结果如下：

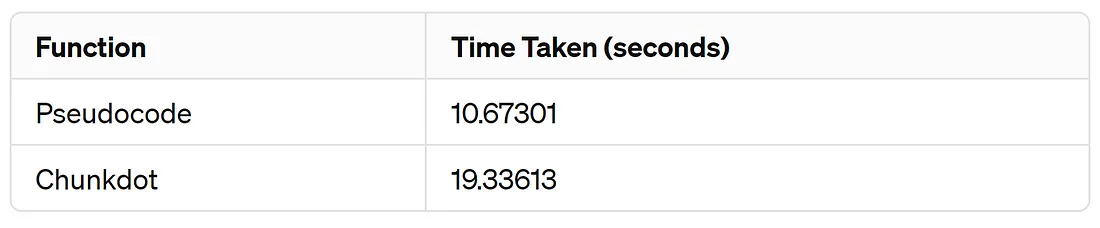
与我们的伪代码相比，Chunkdot 需要花费更多时间。这是因为它首先要创建分块，并在合并之前对每个分块进行计算。因此，对于这个小规模的示例，它可能不是一个合适的解决方案。不过，当我们稍后处理更大的示例时，你就会发现 Chunkdot 的优势。

100K 向量嵌入测试

我们的伪代码方法在处理 10K 个向量时取得了胜利，但现在让我们将文档嵌入向量增加到 100K 个，这相当于一个中等规模的 RAG 应用程序。

让我们计算一下每种方法的计算时间，但这次我们将次数参数设置为 1（运行一次代码），因为向量的数量相当大，没有必要多次执行计算。

doc_embeddings = np.random.randn(100000, 1536) # 100K document embeddings (1536 dim)100000, 1536) # 100K document embeddings (1536 dim)
user_query = np.random.rand(1,1536) # user query (1536 dim)
top_indices = 1 # number of top indices to retrieve 
max_memory = 5E9 # maximum memory set to 5GB
times = 1 # number of times to execute the functions
# compute the time taken to execute the functions
calculate_execution_time(user_query, doc_embeddings, top_indices, max_memory, times)

对于 100k 文档嵌入，维度为 1536，同时运行两种算法，对比结果如下：

与我们的伪代码相比，Chunkdot花费的时间更少，几乎只有一半。现在，我们看到了 Chunkdot 的可喜影响。

百万矢量嵌入测试

在处理涉及数百万个嵌入向量的任务时，首先需要检查的是文档嵌入向量占用了多少内存。

# 1 Million document embeddings (1536 dim)
doc_embeddings = np.random.randn(1000000, 1536)
# user query (1536 dim)
user_query = np.random.rand(1,1536)
# Check the memory size of doc_embeddings and user_query embedding
print(doc_embeddings.nbytes / (1024 * 1024 * 1024),
      user_query.nbytes / (1024 * 1024))

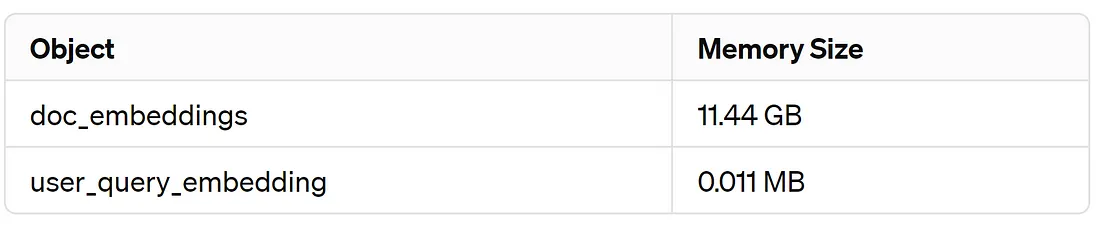
我们的文档嵌入向量大约占用 12GB 内存。让我们检查一下剩余的可用空间。

我们的可用内存高达 17GB。为避免出现任何内存错误，我们将为 max_memory 参数设置一个安全值，即 12GB。让我们看看结果。

# 1 Million document embeddings (1536 dim)
doc_embeddings = np.random.randn(1000000, 1536)
# user query (1536 dim)
user_query = np.random.rand(1,1536)
top_indices = 1 # number of top indices to retrieve 
max_memory = 12E9 # maximum memory set to  --- 12GB ---
times = 1 # number of times to execute the functions
# compute the time taken to execute the functions
calculate_execution_time(user_query, doc_embeddings, top_indices, max_memory, times)

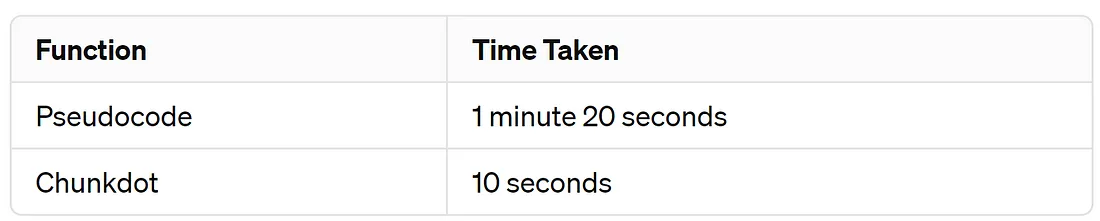
ChunkDot 的确能有效减少计算量。当你打算建立一个严肃的 RAG 应用程序时，你应该考虑从至少一百万次查询开始。使用更高维的嵌入模型，最多可达 4000 次。这种方法将变得更加高效。

可视化可扩展性的影响

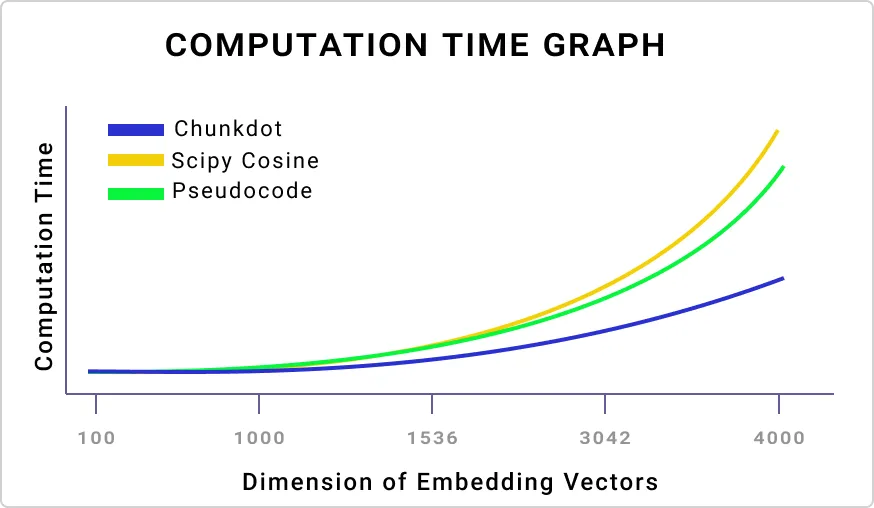
让我们可视化一下增加文档嵌入向量数量的影响，从 10,000 到一个非常大的数字。

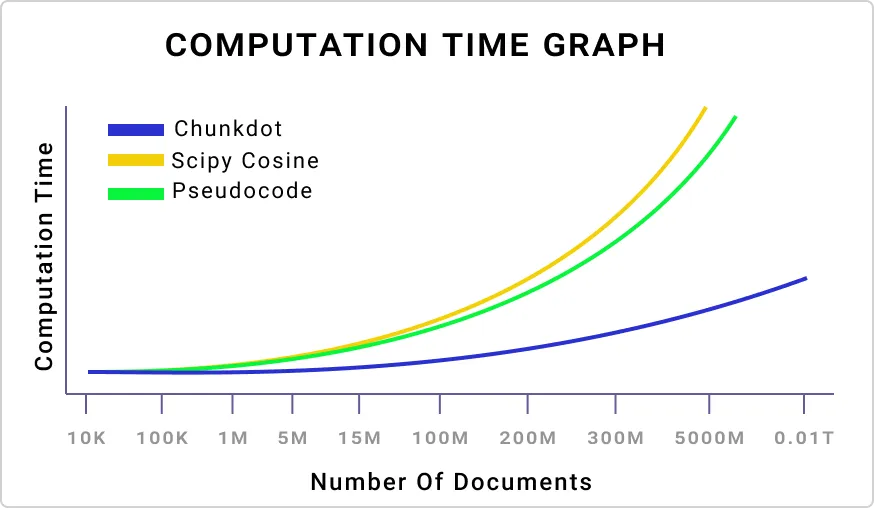
我绘制了三种方法，在增加文档嵌入数量的基础上，Chunkdot 是所有方法中最优秀的。现在，我们来看看嵌入向量的维度对计算时间有什么影响。

Chunkdot 的功能

Chunkdot 有一个可以显示进度条的功能，可以帮助你跟踪剩余的计算量。

doc_embeddings = np.random.randn(100000, 1536) # 100K document embeddings (1536 dim)100000, 1536) # 100K document embeddings (1536 dim)
user_query = np.random.rand(1,1536) # user query (1536 dim)
top_indices = 100 # number of top indices to retrieve 
max_memory = 5E9 # maximum memory set to 5GB
# with progress bar
output_array = cosine_similarity_top_k(user_query, doc_embeddings, 
                        top_k=top_indices, 
                        show_progress=True)

Chunkdot 的输出是一个稀疏矩阵，你可以用它转换成一个数组：

# converting the ouput
output_array.toarray()

你可以只使用 Chunkdot 来处理文档嵌入，它会为文档嵌入的每个元素返回 top_k 个最相似的元素。

# total 5 documents embeddings
embeddings = np.random.randn(5, 256)
# return top 2 most similar item index for each
cosine_similarity_top_k(embeddings, top_k=2).toarray()

### OUTPUT ###
array([[1.        , 0.        , 0.        , 0.        , 0.09924064],
       [0.        , 1.        , 0.        , 0.09935381, 0.        ],
       [0.02358785, 0.        , 1.        , 0.        , 0.        ],
       [0.        , 0.09935381, 0.        , 1.        , 0.        ],
       [0.09924064, 0.        , 0.        , 0.        , 1.        ]])
### OUTPUT ###

同样，你也可以通过为 top_k 参数提供负值来返回最相似的项目

# total 5 documents embeddings
embeddings = np.random.randn(5, 256)
# return top 2 most dissimilar item index for each 
# Top_K = -2
cosine_similarity_top_k(embeddings, top_k=-2).toarray()

### OUTPUT ###
array([[ 0.        ,  0.        , -0.04357524,  0.        , -0.05118288],
       [ 0.        ,  0.        ,  0.        ,  0.01619543, -0.01836534],
       [-0.04357524,  0.        ,  0.        , -0.02466613,  0.        ],
       [ 0.        ,  0.01619543, -0.02466613,  0.        ,  0.        ],
       [-0.05118288, -0.01836534,  0.        ,  0.        ,  0.        ]])
### OUTPUT ###

这可能不是你的情况，但如果你要处理高达 10K 维度的稀疏嵌入，你可以使用密度参数来更有效地减少计算量。

# for creating sparse embeddings
from scipy import sparse
# creating spare matrix with 100K documents (10K dim each)
# defining density of 0.005
embeddings = sparse.rand(100000, 10000, density=0.005)
# using all you system's memory
cosine_similarity_top_k(embeddings, top_k=50)

Chunkdot 的最大优势之一是它可以在 CPU 内核上运行。未来，他们计划整合 GPU 支持，这将大大缩短计算时间。如果你的本地环境没有足够的内存，你可以使用 Kaggle 或 GitHub Codespaces 等平台，与 GPU 相比，云 CPU 内核和内存的成本非常低。别忘了查看 GitHub 官方仓库和博客，因为其中对 Chunkdot 的工作原理做了非常详细的解释。