介绍

PyKrige 是一个开源 Python 库，旨在实现克里金法，这是一种用于插值和预测空间数据的重要地统计技术。克里金法提供了一种利用数据点之间的空间相关性来估计地理区域内变量值的复杂方法。本文深入探讨了 PyKrige 的概念基础、其实现、应用以及与其使用相关的潜在好处和挑战。

概念基础

PyKrige 的理论基础是地质统计学，这是统计学的一个分支，主要研究空间或时空数据集。克里金法本身是以南非工程师丹尼尔-克里金的名字命名的，他是采矿业估算矿石储量的先驱。克里金法的核心是利用数据点之间的空间相关性进行预测。与简单的插值法不同，克里金法提供的估算可以考虑空间趋势和变异性，从而更细致、更准确地反映所研究的空间现象。

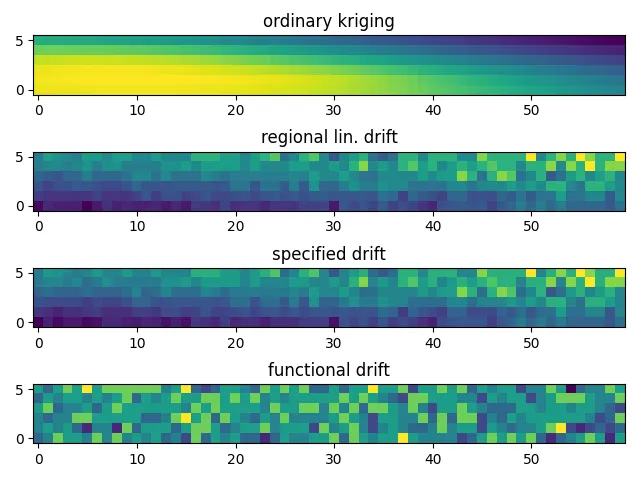
PyKrige 实现了克里金法的几种变体，包括普通克里金法、通用克里金法和协同克里金法。普通克里金法假定整个相关区域的平均值不变，而通用克里金法允许平均值在空间上变化，通常以坐标的多项式函数建模。另一方面，协同克里金法涉及使用与主要相关变量相关的次要变量，从而有可能提高预测精度。

实施

PyKrige 在设计时考虑到了易用性，提供了一个高级界面，简化了克里金分析的过程。该库兼容各种基于 Python 的科学计算堆栈，包括 NumPy、SciPy 和 pandas，便于将其集成到更广泛的数据分析工作流中。PyKrige 还支持二维和三维克里金分析，可满足从地表高程建模到地下地质分析等广泛的应用需求。

该库的实现强调灵活性，允许用户自定义克里金过程的关键参数，如变异图模型。变异图是克里金法的一个基本概念，描述了空间相关性如何随距离变化。通过对数据拟合变异图模型，PyKrige 使用户能够捕捉到潜在的空间结构，这对精确插值至关重要。

应用

PyKrige 的应用领域广泛，包括环境科学、水文学、地质学和农业。例如，它可用于预测未监测地区的污染水平，根据稀疏的气象站数据估算降雨分布，为采矿勘探中的矿石品位建模，或根据土壤养分的变化优化农业投入的位置。

PyKrige 的灵活性和准确性使其成为研究人员和从业人员预测空间现象的重要工具。PyKrige 与更广泛的 Python 生态系统集成的能力进一步增强了其实用性，使复杂的地理空间数据分析管道得以构建。

优势与挑战

PyKrige 的主要优势在于它能够提供准确的空间插值，考虑到数据固有的可变性和趋势。在空间可变性较大的领域，这可以帮助做出更明智的决策。此外，PyKrige 的开源性质营造了一个协作环境，用户可以为其开发献计献策，确保该库不断发展，以满足其用户群不断变化的需求。

然而，PyKrige 和克里金法的使用并非没有挑战。有效的克里金法需要充分了解所建模的空间过程，包括选择适当的变分模型。错误应用或过度简化这些模型会导致预测不准确。此外，克里金法可能需要大量计算，特别是对于大型数据集或复杂的变异函数模型，这可能会限制其在资源有限的环境中的使用。

代码

为了演示如何使用 PyKrige 对合成数据集进行空间插值，我们将介绍整个过程，包括生成合成数据集、使用 PyKrige 进行克里金法，以及用度量和绘图来评估结果。本示例将侧重于二维空间数据，这是许多地理空间分析中的典型数据。

首先，确保已安装 PyKrige。可以使用 pip 安装：

pip install pykrige

让我们开始实施吧：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Generate synthetic data: 50 points
np.random.seed(42)  # For reproducibility
x_coords = np.random.uniform(0, 100, 50)
y_coords = np.random.uniform(0, 100, 50)
values = np.sin(x_coords * 0.1) + np.cos(y_coords * 0.1) + np.random.normal(0, 0.1, 50)
# Plotting the synthetic data
plt.scatter(x_coords, y_coords, c=values, cmap='viridis')
plt.colorbar(label='Value')
plt.xlabel('X Coordinate')
plt.ylabel('Y Coordinate')
plt.title('Synthetic Spatial Data')
plt.show()

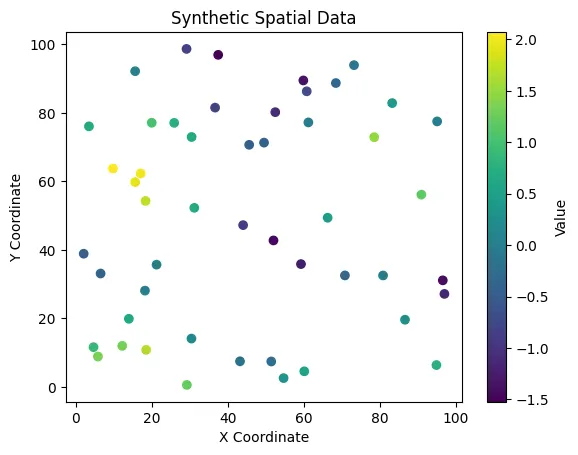
为了演示的目的，我们假设在未知位置有一些 "真实 "值与克里格估计值进行比较。由于这是一个合成示例，我们将跳过这一步，但在实践中，你可以使用平均平方误差 (MSE) 或平均绝对误差 (MAE) 等指标来评估内插值与已知测量值之间的准确性。

from pykrige.ok import OrdinaryKriging
from pykrige.kriging_tools import write_asc_grid
import pykrige.kriging_tools as kt
# Create the Ordinary Kriging object
OK = OrdinaryKriging(
    x_coords,
    y_coords,
    values,
    variogram_model='linear',
    verbose=False,
    enable_plotting=False
)
# Generate a grid
gridx = np.linspace(0, 100, 100)
gridy = np.linspace(0, 100, 100)
# Perform kriging
z, ss = OK.execute('grid', gridx, gridy)
# z is the interpolated values
# ss is the squared error
plt.figure(figsize=(10, 8))
plt.imshow(z, extent=(0, 100, 0, 100), origin='lower', cmap='viridis')
plt.scatter(x_coords, y_coords, c='red')  # original data points
plt.colorbar(label='Interpolated Value')
plt.title('Kriging Interpolation of Synthetic Data')
plt.xlabel('X Coordinate')
plt.ylabel('Y Coordinate')
plt.show()

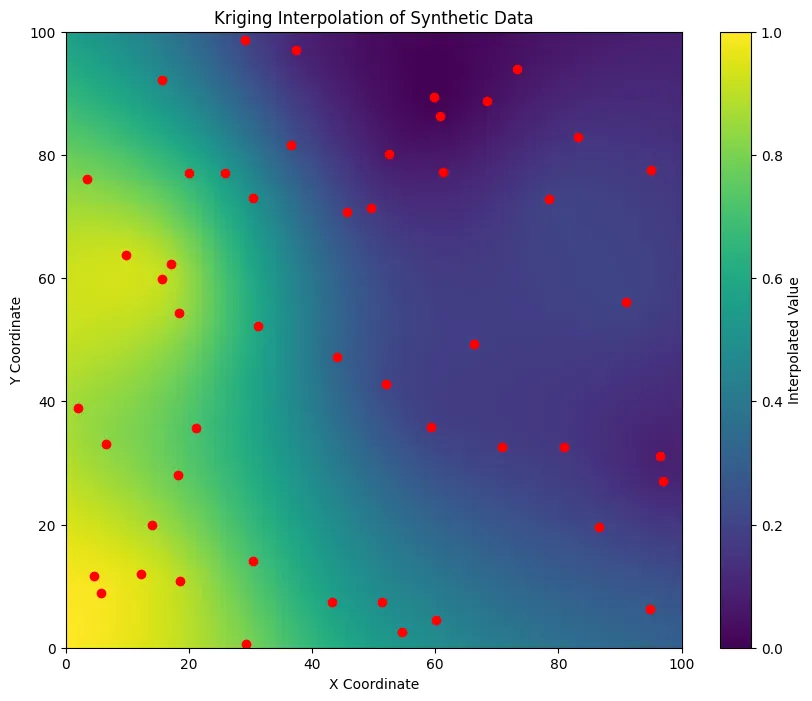
本示例演示了如何使用 PyKrige 进行空间插值，从生成合成数据集到执行克里金法和可视化结果。本例使用了一个简单的线性变异图模型和一个合成数据集，PyKrige 支持各种选项和配置，以微调现实世界数据集的插值过程。

结论

PyKrige 是地理统计分析领域的一个强大工具，为应用克里金进行空间插值和预测提供了一种便捷的方法。它与 Python 生态系统的集成允许进行复杂的空间数据分析，有利于广泛的科学和工业应用。虽然用户必须掌握复杂的克里金方法和计算要求，但从精确的空间建模中获得的潜在洞察力使 PyKrige 成为地理空间分析师和研究人员工具包中的宝贵财富。