介绍

时间序列分析是统计学和机器学习领域的一种基本方法，旨在了解和预测随时间演变的数据模式。鉴于时间序列数据的独特性，包括趋势、季节性和自相关性，传统的交叉验证技术往往无法提供准确可靠的性能估计。为了应对这些挑战，时间序列交叉验证成为一种关键的方法，它是为尊重数据固有的时间顺序而量身定制的。本文将深入探讨时间序列交叉验证的复杂性，重点介绍其意义、方法、变化和实际考虑因素。

重要意义

时间序列交叉验证的主要目的是以反映未来应用的方式评估模型的预测性能。这在金融、气象和流行病学等多个领域都至关重要，因为这些领域的决策都是基于预测的。传统的交叉验证方法会随机分割数据，可能会破坏时间序列，导致过于乐观的性能估计和模型在真实世界的时间动态下失效。时间序列交叉验证保留了时间顺序，确保预测始终基于过去的信息，从而对模型的预测能力进行更真实的评估。

方法论

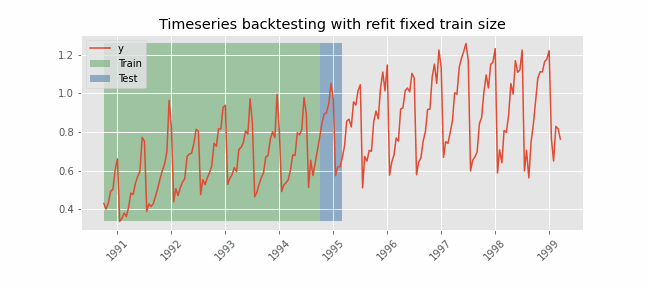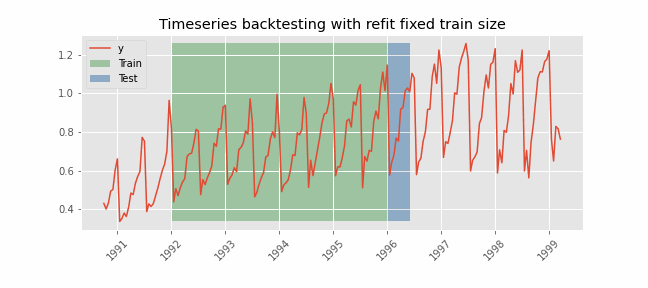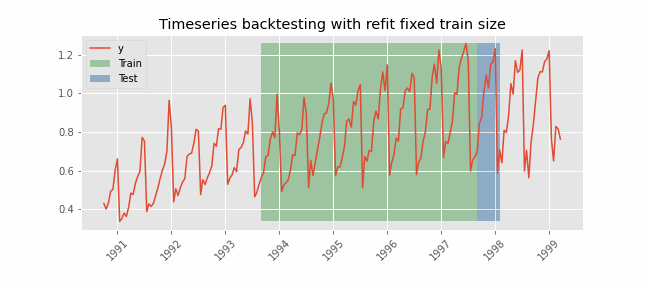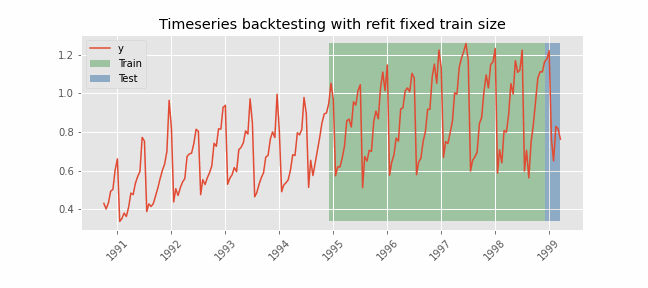
时间序列交叉验证的精髓在于其按顺序划分数据集的方法。与随机划分不同的是，它系统地扩展了训练数据集，使其包括更近期的观测数据，而测试集则由紧随训练集之后的观测数据组成。这个过程会反复进行，每次都会将训练集和测试集之间的分界点提前。这种方法可确保模型在不同时期得到验证，从而捕捉数据中的各种时间动态和潜在结构变化。

变化

时间序列交叉验证的几种变体可满足时间相关数据集的特定需求和限制：

• 单步预测： 这是最直接的方法，即在单个连续时间点上对模型进行训练和验证。它尤其适用于评估模型在提前一步预测中的性能。
• 多步骤预测： 在多步骤预测中，每次迭代都会对模型的多个未来时间点进行测试。这种变化对于评估模型在较长时期内的性能至关重要，而这对于战略规划和决策至关重要。
• 滚动原点： 这种方法也称为 "滚动预测原点 "交叉验证法，即在每次迭代时将测试集的起点向前移动一个或多个时间段。它可以全面评估模型随时间变化的稳定性和可靠性。
• 扩大窗口： 与滚动原点技术相反，扩展窗口变化保留了训练集中的所有前期数据，并逐步扩大其规模。这种方法有利于捕捉长期趋势和季节性。

实际考虑因素

实施时间序列交叉验证需要注意几个实际方面：

• 季节性和趋势： 应在不同季节和趋势阶段对模型进行评估，以确保其对时间变化的稳健性。
  
• 静态性： 确保时间序列是静态的，即其统计特性不会随时间变化，这对交叉验证结果的可靠性至关重要。
• 计算效率： 时间序列交叉验证的计算量很大，尤其是对于大型数据集和复杂模型。高效的实施和优化技术对实际可用性至关重要。
• 参数调整： 可以在时间序列框架内使用嵌套交叉验证来优化模型参数，从而进一步提高预测准确性。

代码

为了用一个完整的 Python 代码示例来说明时间序列交叉验证，我们将生成一个合成的时间序列数据集，实施时间序列交叉验证，训练一个简单的模型，使用适当的指标对其进行评估，并将结果可视化。本示例将使用常用的 Python 库，如 pandas、numpy、matplotlib 和 sklearn。

让我们开始学习代码：

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
import matplotlib.pyplot as plt
# Step 1: Generate Synthetic Dataset
np.random.seed(42)  # For reproducibility
time = np.arange(100)
trend = time * 0.5
seasonality = 10 * np.sin(np.pi * time / 6)
noise = np.random.normal(loc=0, scale=5, size=time.size)
data = trend + seasonality + noise
dates = pd.date_range(start='2020-01-01', periods=time.size, freq='D')
ts_data = pd.Series(data, index=dates)
# Step 2: Time Series Cross-Validation Setup
def time_series_cv(X, y, model, n_splits):
    test_scores = []
    
    tscv = TimeSeriesSplit(n_splits=n_splits)
    
    for train_idx, test_idx in tscv.split(X):
        X_train, X_test = X[train_idx], X[test_idx]
        y_train, y_test = y[train_idx], y[test_idx]
        
        model.fit(X_train, y_train)
        y_pred = model.predict(X_test)
        test_score = mean_squared_error(y_test, y_pred)
        test_scores.append(test_score)
    
    return test_scores
# Preparing data for modeling
X = time.reshape(-1, 1)
y = data
# Step 3: Model Training
model = LinearRegression()
# Import TimeSeriesSplit
from sklearn.model_selection import TimeSeriesSplit
n_splits = 5
scores = time_series_cv(X, y, model, n_splits=n_splits)
# Step 4: Evaluate Model Performance
print(f'MSE Scores for each split: {scores}')
print(f'Average MSE: {np.mean(scores)}')
# Step 5: Visualize the Results
plt.figure(figsize=(10, 6))
plt.plot(dates, data, label='True Value', color='blue')
plt.plot(dates, model.predict(X), label='Predicted Value', color='red', linestyle='--')
plt.title('Time Series Cross-Validation: True vs Predicted')
plt.legend()
plt.show()

该代码的功能如下：

• 生成具有趋势、季节性和噪声的合成时间序列数据集。
• 使用 sklearn 的 TimeSeriesSplit 执行滚动预测起源交叉验证策略。
• 在时间序列数据上训练线性回归模型。
• 使用平均平方误差 (MSE) 指标评估模型的性能。
• 可视化时间序列的真实值与预测值。

MSE Scores for each split: [113.85938733387366, 125.52615877943208, 70.17575280052887, 74.29515859510016, 78.3146223127321]for each split: [113.85938733387366, 125.52615877943208, 70.17575280052887, 74.29515859510016, 78.3146223127321]
Average MSE: 92.43421596433339

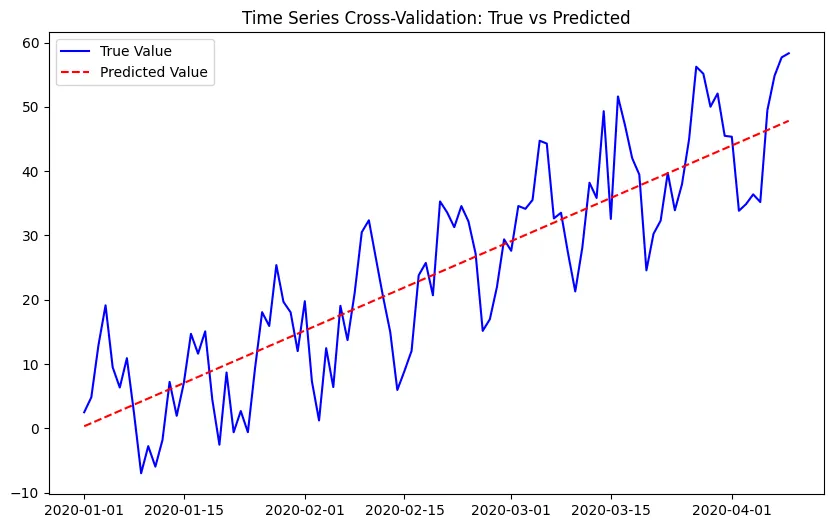
请记住，本例使用简单的线性回归模型进行演示。实际上，你可以根据时间序列数据的特点和预测任务的具体要求来选择模型。

结论

时间序列交叉验证是评估和开发时间相关数据集预测模型的基础技术。通过尊重观测数据的时间顺序，它可以对模型性能进行严格而现实的评估。随着预测建模的不断发展，时间序列交叉验证的完善和应用无疑将在利用时间序列分析的全部潜力进行预测和决策方面发挥至关重要的作用。