自从2017年《Attention is All You Need》提出以来，Transformer 模型已经成为自然语言处理（NLP）领域的最先进技术。在2021年，《An Image is Worth 16x16 Words》2 成功将 Transformer 模型应用到了计算机视觉任务中。此后，许多基于 Transformer 的架构也被提出用于计算机视觉。

本文将深入探讨注意力层在计算机视觉中的工作原理。我们将涵盖单头和多头注意力，并提供了注意力层的开源代码，以及底层数学的概念性解释。代码使用了 Python 的 PyTorch 包。

注意事项

在自然语言处理（NLP）应用中，注意力通常被描述为句子中单词（标记）之间的关系。在计算机视觉应用中，注意力关注的是图像中各个区块（标记）之间的关系。

将图像分解为一系列标记有多种方法。最初的 ViT 将图像分割为各个区块，然后将其展平为标记；而 Tokens-to-Token ViT 则采用了更复杂的方法来从图像中创建标记；有关该方法的更多信息可以在《Tokens-To-Token ViT》文章中找到。

本文将在假定标记为输入的情况下继续讨论注意力层。在 Transformer 的开始阶段，这些标记将代表输入图像中的区块。然而，更深层的注意力层将计算已经被前面层修改过的标记之间的注意力，从而消除了表示的直接性。

本文将详细探讨《Attention is All You Need》 中定义的点积（等效于乘法）注意力。这与《An Image is Worth 16x16 Words》 和 Tokens-to-Token ViT等衍生作品中使用的相同注意力机制。代码基于公开可用的 Tokens-to-Token ViT 的 GitHub 代码，经过一些修改。对源代码的更改包括但不限于将两个注意力模块合并为一个，并实现多头注意力。

完整的注意力模块如下所示：

class Attention(nn.Module):
    def __init__(self, 
                dim: int,
                chan: int,
                num_heads: int=1,
                qkv_bias: bool=False,
                qk_scale: NoneFloat=None):
        """ Attention Module
            Args:
                dim (int): input size of a single token
                chan (int): resulting size of a single token (channels)
                num_heads(int): number of attention heads in MSA
                qkv_bias (bool): determines if the qkv layer learns an addative bias
                qk_scale (NoneFloat): value to scale the queries and keys by; 
                                    if None, queries and keys are scaled by ``head_dim ** -0.5``
        """
        super().__init__()
        ## Define Constants
        self.num_heads = num_heads
        self.chan = chan
        self.head_dim = self.chan // self.num_heads
        self.scale = qk_scale or self.head_dim ** -0.5
        assert self.chan % self.num_heads == 0, '"Chan" must be evenly divisible by "num_heads".'
        ## Define Layers
        self.qkv = nn.Linear(dim, chan * 3, bias=qkv_bias)
        #### Each token gets projected from starting length (dim) to channel length (chan) 3 times (for each Q, K, V)
        self.proj = nn.Linear(chan, chan)
    def forward(self, x):
        B, N, C = x.shape
        ## Dimensions: (batch, num_tokens, token_len)
        ## Calcuate QKVs
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, self.head_dim).permute(2, 0, 3, 1, 4)
        #### Dimensions: (3, batch, heads, num_tokens, chan/num_heads = head_dim)
        q, k, v = qkv[0], qkv[1], qkv[2]
        ## Calculate Attention
        attn = (q * self.scale) @ k.transpose(-2, -1)
        attn = attn.softmax(dim=-1)
        #### Dimensions: (batch, heads, num_tokens, num_tokens)
        ## Attention Layer
        x = (attn @ v).transpose(1, 2).reshape(B, N, self.chan)
        #### Dimensions: (batch, heads, num_tokens, chan)
        ## Projection Layers
        x = self.proj(x)
        ## Skip Connection Layer
        v = v.transpose(1, 2).reshape(B, N, self.chan)
        x = v + x     
        #### Because the original x has different size with current x, use v to do skip connection
        return x

单头注意力 

从只有一个注意力头开始，让我们逐行分析前向传播，并在此过程中查看一些矩阵图。我们使用 7∗7=49 作为我们的起始标记大小，因为这是 T2T-ViT 模型中的起始标记大小。我们使用 64 个通道，因为这也是 T2T-ViT 的默认值。我们使用 100 个标记，因为这是一个不错的数字。我们使用批量大小为 13，因为它是质数，不会与其他参数混淆。

# Define an Input
token_len = 7*7
channels = 64
num_tokens = 100
batch = 13
x = torch.rand(batch, num_tokens, token_len)
B, N, C = x.shape
print('Input dimensions are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\ttoken size:', x.shape[2])
# Define the Module
A = Attention(dim=token_len, chan=channels, num_heads=1, qkv_bias=False, qk_scale=None)
A.eval();

Input dimensions are
   batchsize: 13 
   number of tokens: 100 
   token size: 49

从《Attention is All You Need》中，注意力是通过查询（Queries）、键（Keys）和值（Values）矩阵来定义的。首先，我们通过一个可学习的线性层来计算这些矩阵。布尔值 qkv_bias 表示这些线性层是否具有偏置项。此步骤还将输入的标记长度从 49 改变为我们设置的 64。

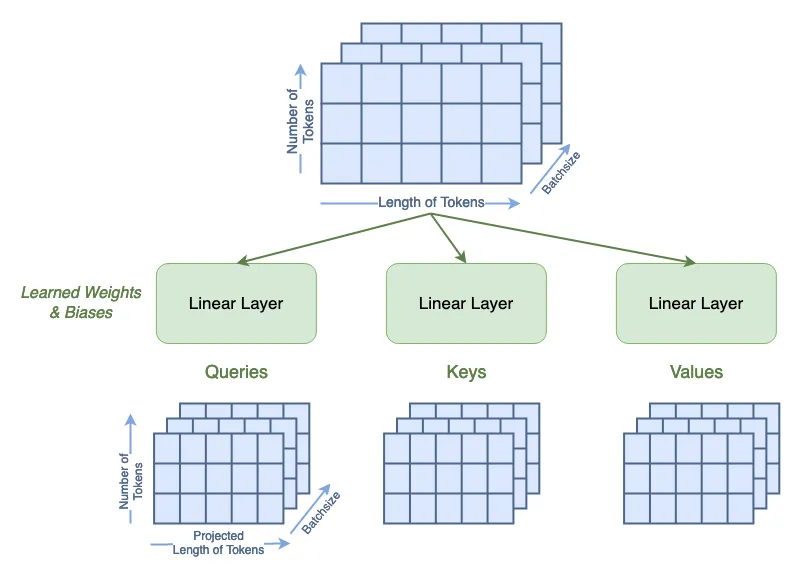
qkv = A.qkv(x).reshape(B, N, 3, A.num_heads, A.head_dim).permute(2, 0, 3, 1, 4)3, A.num_heads, A.head_dim).permute(2, 0, 3, 1, 4)
q, k, v = qkv[0], qkv[1], qkv[2]
print('Dimensions for Queries are\n\tbatchsize:', q.shape[0], '\n\tattention heads:', q.shape[1], '\n\tnumber of tokens:', q.shape[2], '\n\tnew length of tokens:', q.shape[3])
print('See that the dimensions for queries, keys, and values are all the same:')
print('\tShape of Q:', q.shape, '\n\tShape of K:', k.shape, '\n\tShape of V:', v.shape)

Dimensions for Queries are
   batchsize: 13 
   attention heads: 1 
   number of tokens: 100 
   new length of tokens: 64
See that the dimensions for queries, keys, and values are all the same:
   Shape of Q: torch.Size([13, 1, 100, 64]) 
   Shape of K: torch.Size([13, 1, 100, 64]) 
   Shape of V: torch.Size([13, 1, 100, 64])

现在，我们可以开始计算注意力，其定义如下：

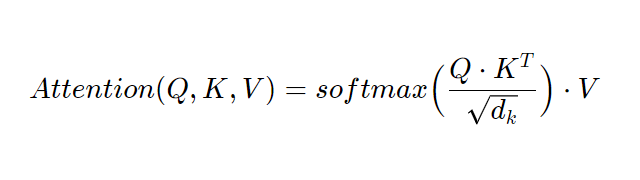
在这个公式中，Q、K 和 V 分别表示查询、键和值；dk​ 是键的维度，等于键标记的长度，也等于 chan 的长度。

我们将按照代码中的实现逐步解析这个方程。我们将把中间矩阵称为 Attn。

首先，我们要计算：

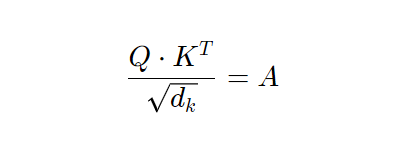
在代码中设置了：

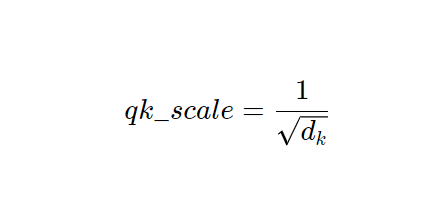
默认情况下：

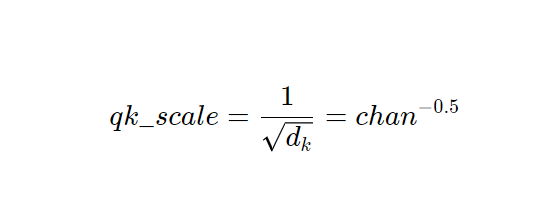
然而，用户可以将替代的缩放值作为超参数进行指定。

分子中的矩阵乘法 Q·Kᵀ 如下所示：

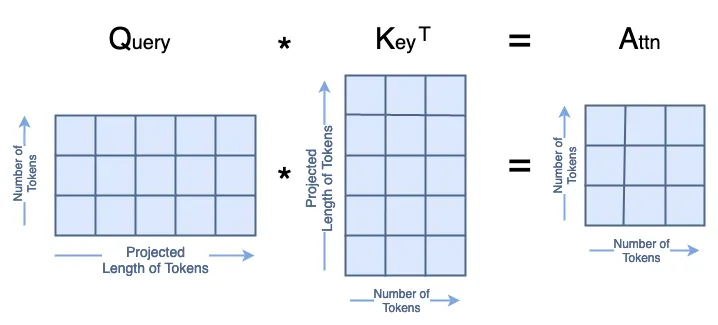
所有这些在代码中看起来像：

attn = (q * A.scale) @ k.transpose(-2, -1)2, -1)
print('Dimensions for Attn are\n\tbatchsize:', attn.shape[0], '\n\tattention heads:', attn.shape[1], '\n\tnumber of tokens:', attn.shape[2], '\n\tnumber of tokens:', attn.shape[3])

Dimensions for Attn are
   batchsize: 13 
   attention heads: 1 
   number of tokens: 100 
   number of tokens: 100

接下来，我们计算 A 的 softmax，这不会改变它的形状。

attn = attn.softmax(dim=-1)1)
print('Dimensions for Attn are\n\tbatchsize:', attn.shape[0], '\n\tattention heads:', attn.shape[1], '\n\tnumber of tokens:', attn.shape[2], '\n\tnumber of tokens:', attn.shape[3])

Dimensions for Attn are
   batchsize: 13 
   attention heads: 1 
   number of tokens: 100 
   number of tokens: 100

最后，我们计算 A·V=x，如下所示：

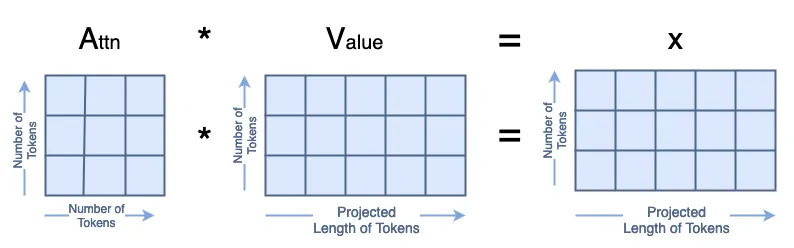
x = attn @ v
print('Dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tattention heads:', x.shape[1], '\n\tnumber of tokens:', x.shape[2], '\n\tlength of tokens:', x.shape[3])

Dimensions for x are
   batchsize: 13 
   attention heads: 1 
   number of tokens: 100 
   length of tokens: 64

输出 x 被重塑以删除注意力头维度。

x = x.transpose(1, 2).reshape(B, N, A.chan)1, 2).reshape(B, N, A.chan)
print('Dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\tlength of tokens:', x.shape[2])

Dimensions for x are
   batchsize: 13 
   number of tokens: 100 
   length of tokens: 64

然后我们将 x 输入一个可学习的线性层，该层不会改变它的形状。

x = A.proj(x)
print('Dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\tlength of tokens:', x.shape[2])

Dimensions for x are
   batchsize: 13 
   number of tokens: 100 
   length of tokens: 64

最后，我们实现了一个跳跃连接。由于当前的 x 形状与输入 x 的形状不同，我们使用 V 来进行跳跃连接。我们在注意力头维度上对 V 进行了展平。

orig_shape = (batch, num_tokens, token_len)
curr_shape = (x.shape[0], x.shape[1], x.shape[2])0], x.shape[1], x.shape[2])
v = v.transpose(1, 2).reshape(B, N, A.chan)
v_shape = (v.shape[0], v.shape[1], v.shape[2])
print('Original shape of input x:', orig_shape)
print('Current shape of x:', curr_shape)
print('Shape of V:', v_shape)
x = v + x     
print('After skip connection, dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\tlength of tokens:', x.shape[2])

Original shape of input x: (13, 100, 49)
Current shape of x: (13, 100, 64)
Shape of V: (13, 100, 64)
After skip connection, dimensions for x are
   batchsize: 13 
   number of tokens: 100 
   length of tokens: 64

多头注意力

在计算机视觉中，多头注意力通常被称为多头自注意力（Multi-headed Self Attention，MSA）。

与单头注意力相同，我们使用 7∗7=49 作为起始标记大小，64 个通道是 T2T-ViT 的默认值³。我们使用 100 个标记，因为这是一个不错的数字。我们使用批量大小为 13，因为它是质数，不会与其他参数混淆。

注意力头的数量必须能够整除通道数，因此在本示例中，我们将使用 4 个注意力头。

# Define an Input
token_len = 7*7
channels = 64
num_tokens = 100
batch = 13
num_heads = 4
x = torch.rand(batch, num_tokens, token_len)
B, N, C = x.shape
print('Input dimensions are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\ttoken size:', x.shape[2])
# Define the Module
MSA = Attention(dim=token_len, chan=channels, num_heads=num_heads, qkv_bias=False, qk_scale=None)
MSA.eval();

Input dimensions are
   batchsize: 13 
   number of tokens: 100 
   token size: 49

计算查询（Queries）、键（Keys）和值（Values）的过程与单头注意力中相同。然而，你可以看到标记的新长度为 chan/num_heads。Q、K 和 V 矩阵的总大小没有改变；它们的内容只是在头维度上分布。你可以将其视为将单头矩阵分割为多个头：

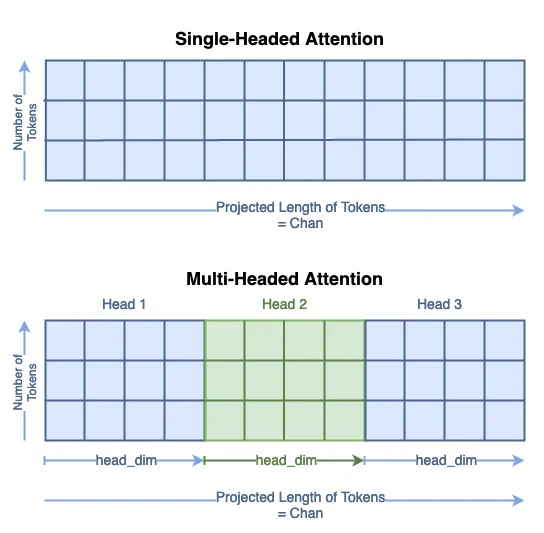
我们将查询头 i 的子矩阵表示为 Qₕᵢ。

qkv = MSA.qkv(x).reshape(B, N, 3, MSA.num_heads, MSA.head_dim).permute(2, 0, 3, 1, 4)3, MSA.num_heads, MSA.head_dim).permute(2, 0, 3, 1, 4)
q, k, v = qkv[0], qkv[1], qkv[2]
print('Head Dimension = chan / num_heads =', MSA.chan, '/', MSA.num_heads, '=', MSA.head_dim)
print('Dimensions for Queries are\n\tbatchsize:', q.shape[0], '\n\tattention heads:', q.shape[1], '\n\tnumber of tokens:', q.shape[2], '\n\tnew length of tokens:', q.shape[3])
print('See that the dimensions for queries, keys, and values are all the same:')
print('\tShape of Q:', q.shape, '\n\tShape of K:', k.shape, '\n\tShape of V:', v.shape)

Head Dimension = chan / num_heads = 64 / 4 = 16
Dimensions for Queries are
   batchsize: 13 
   attention heads: 4 
   number of tokens: 100 
   new length of tokens: 16
See that the dimensions for queries, keys, and values are all the same:
   Shape of Q: torch.Size([13, 4, 100, 16]) 
   Shape of K: torch.Size([13, 4, 100, 16]) 
   Shape of V: torch.Size([13, 4, 100, 16])

下一步计算：

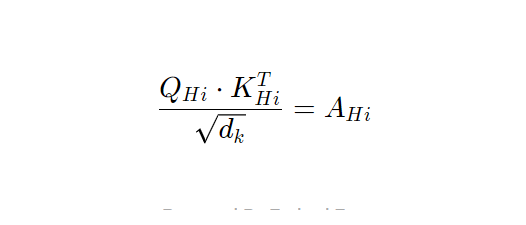
对于每个头我。在这种情况下，密钥的长度是：

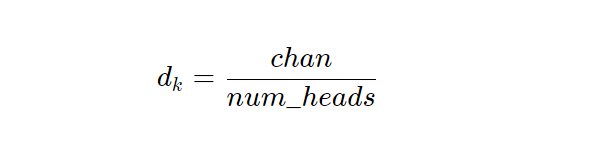
与单头注意力一样，我们使用默认值

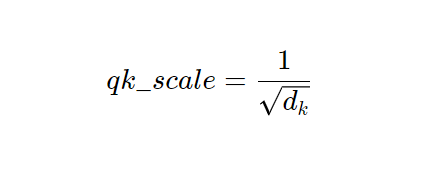
然而，用户可以将替代的缩放值作为超参数进行指定。

我们在这一步中得到了 num_heads = 4 个不同的 Attn 矩阵，如下所示：

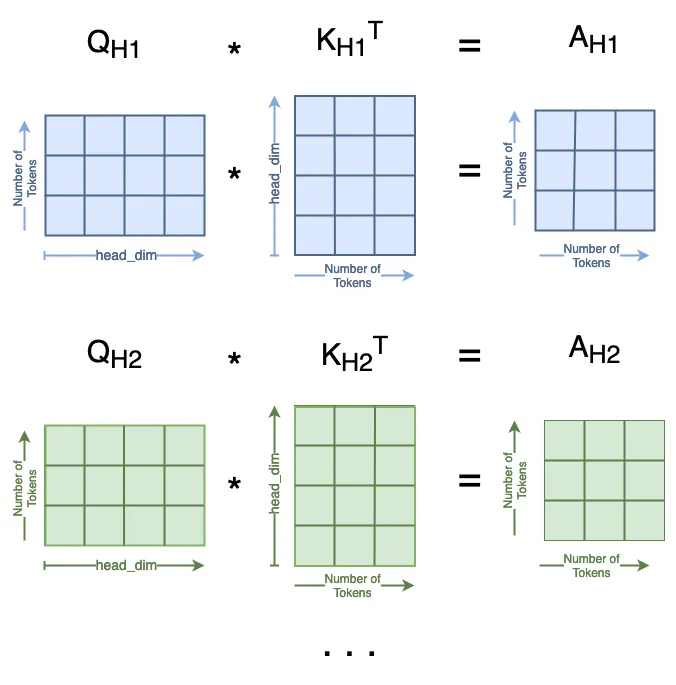
attn = (q * MSA.scale) @ k.transpose(-2, -1)2, -1)
print('Dimensions for Attn are\n\tbatchsize:', attn.shape[0], '\n\tattention heads:', attn.shape[1], '\n\tnumber of tokens:', attn.shape[2], '\n\tnumber of tokens:', attn.shape[3])

Dimensions for Attn are
   batchsize: 13 
   attention heads: 4 
   number of tokens: 100 
   number of tokens: 100

接下来我们计算 A 的 softmax，这不会改变它的形状。

然后，我们可以计算

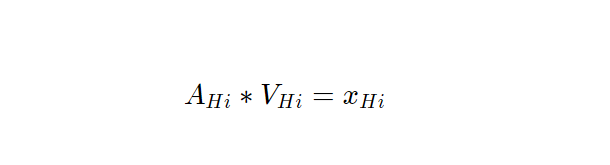
这在多个注意力头中也有类似的分布：

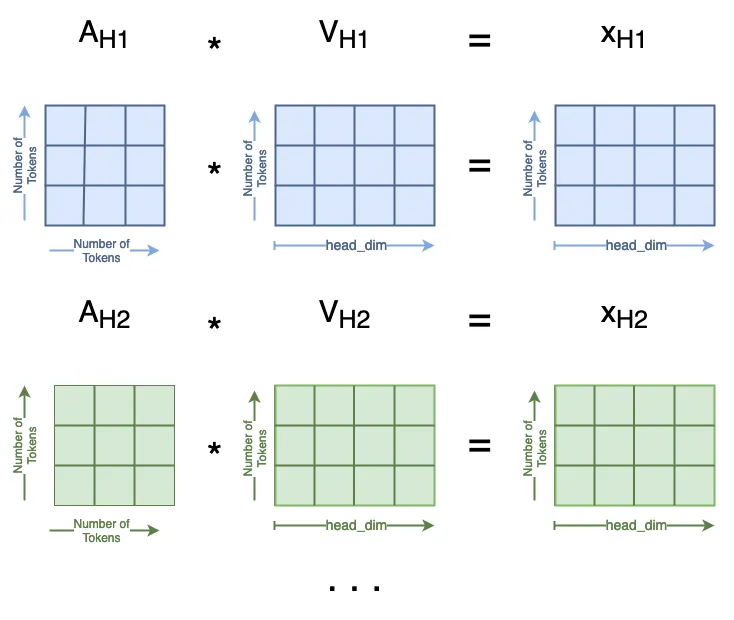
attn = attn.softmax(dim=-1)1)
x = attn @ v
print('Dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tattention heads:', x.shape[1], '\n\tnumber of tokens:', x.shape[2], '\n\tlength of tokens:', x.shape[3])

Dimensions for x are
   batchsize: 13 
   attention heads: 4 
   number of tokens: 100 
   length of tokens: 16

现在，我们通过一些重塑操作将所有的 xₕᵢ 连接在一起。这是与第一步相反的操作：

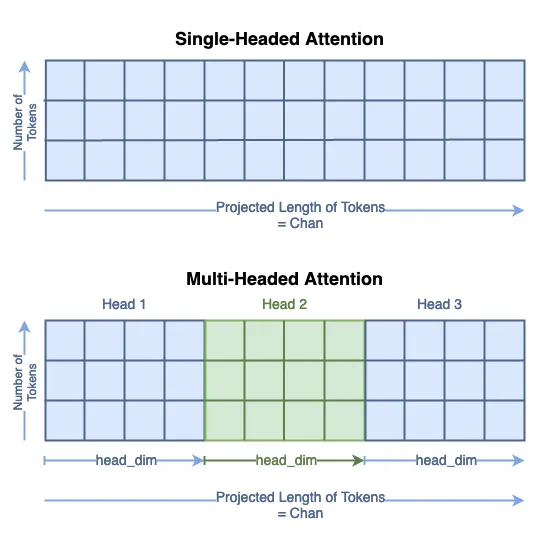
x = x.transpose(1, 2).reshape(B, N, MSA.chan)1, 2).reshape(B, N, MSA.chan)
print('Dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\tlength of tokens:', x.shape[2])

Dimensions for x are
   batchsize: 13 
   number of tokens: 100 
   length of tokens: 64

现在，我们已经将所有注意力头连接在一起，注意力模块的其余部分保持不变。对于跳跃连接，我们仍然使用 V，但我们需要对其进行重塑以去除头维度。

x = MSA.proj(x)
print('Dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\tlength of tokens:', x.shape[2])
orig_shape = (batch, num_tokens, token_len)
curr_shape = (x.shape[0], x.shape[1], x.shape[2])
v = v.transpose(1, 2).reshape(B, N, A.chan)
v_shape = (v.shape[0], v.shape[1], v.shape[2])
print('Original shape of input x:', orig_shape)
print('Current shape of x:', curr_shape)
print('Shape of V:', v_shape)
x = v + x     
print('After skip connection, dimensions for x are\n\tbatchsize:', x.shape[0], '\n\tnumber of tokens:', x.shape[1], '\n\tlength of tokens:', x.shape[2])

Dimensions for x are
   batchsize: 13 
   number of tokens: 100 
   length of tokens: 64
Original shape of input x: (13, 100, 49)
Current shape of x: (13, 100, 64)
Shape of V: (13, 100, 64)
After skip connection, dimensions for x are
   batchsize: 13 
   number of tokens: 100 
   length of tokens: 64

结论

这篇文章详细介绍了视觉 transformer 中注意力层的每个步骤。注意力层中的可学习权重位于从标记到查询、键和值的第一个投影以及最终投影中。大部分注意力层是确定性的矩阵乘法。然而，当使用长标记时，线性层中可能包含大量权重。QKV 投影层中的权重数量等于 input_token_len * chan * 3，最终投影层中的权重数量等于 chan²。