在生成式人工智能、数据科学、机器学习和分析的多元世界中，理解数据点之间的距离和关系至关重要。这就是大型语言模型（LLM）理解上下文和检索数据的方式。大量非结构化数据可以很容易地存储在以三维空间表示的矢量数据库中。

每当用户提出查询，数据库就会检索出最接近的答案。数据是如何存储的，以及这种计算是如何检索到特定信息是令人惊奇的。

有许多先进的方法可以计算向量之间的距离。在本文中，我们将探讨一些重要的距离度量，如Manhattan distance（距离）, Euclidean distance, Cosine distance 和 dot product。

什么是机器学习中的向量？

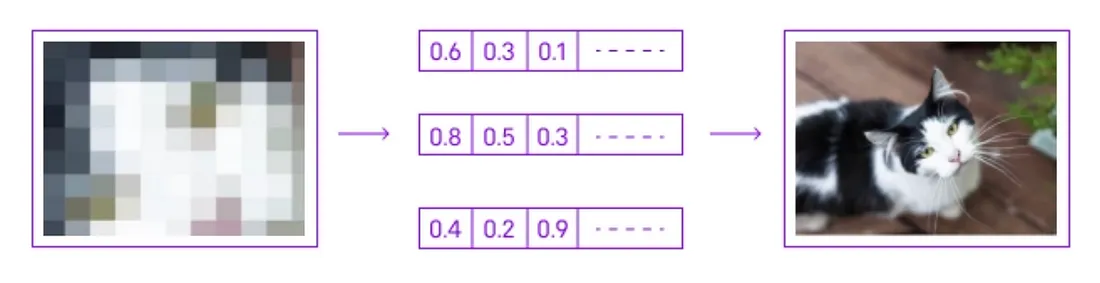
在生成式人工智能领域，向量作为表示和处理复杂数据的一种手段，发挥着至关重要的作用。在这种情况下，向量通常是编码大量信息的高维数字阵列。例如，在生成图像时，每张图像都可以转换成一个向量，代表其像素值或通过深度学习模型提取的更抽象的特征。

这些向量成为人工智能算法理解和生成新内容的语言。通过在多维空间中浏览和修改这些向量，生成式人工智能可以生成新的、合成的数据实例，无论是图像、声音还是文本，都能模仿原始数据集的特征。这种向量操作是人工智能从数据中学习并根据学习结果生成现实输出的核心能力。

什么是向量相似性搜索？

查询涉及在高维空间中找到与给定向量最近的邻居。这一过程被称为向量相似性搜索或近似近邻（ANN）搜索，寻找与查询向量距离（如欧氏距离或余弦相似性）最近的向量。这种方法可以捕捉到不同数据点之间在上下文或特征上的相似性，对于推荐系统、相似性搜索和聚类等任务至关重要。

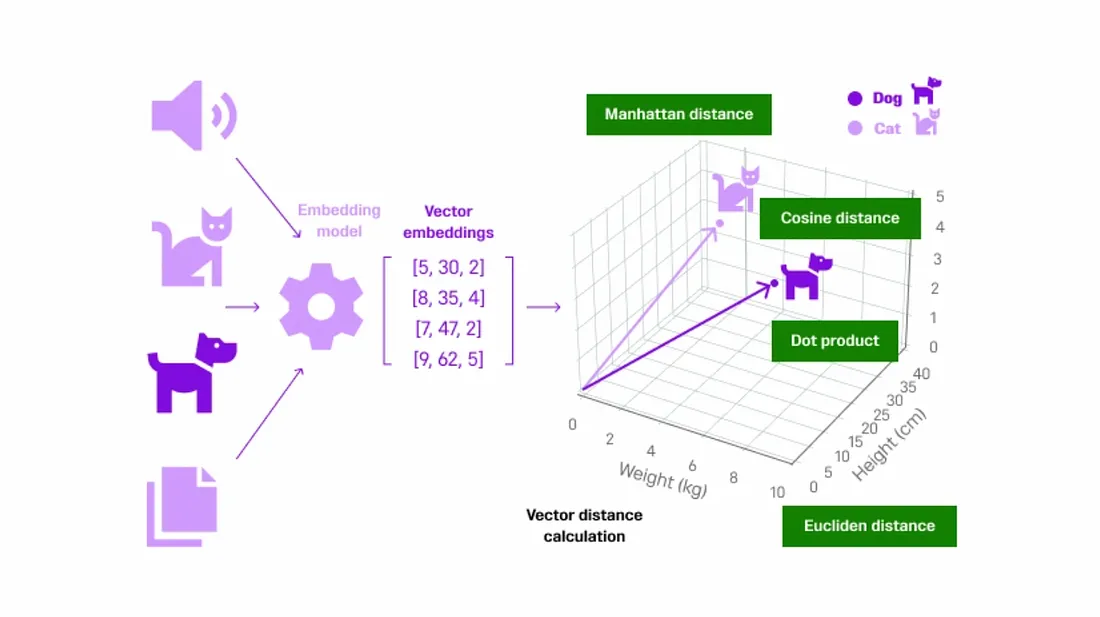
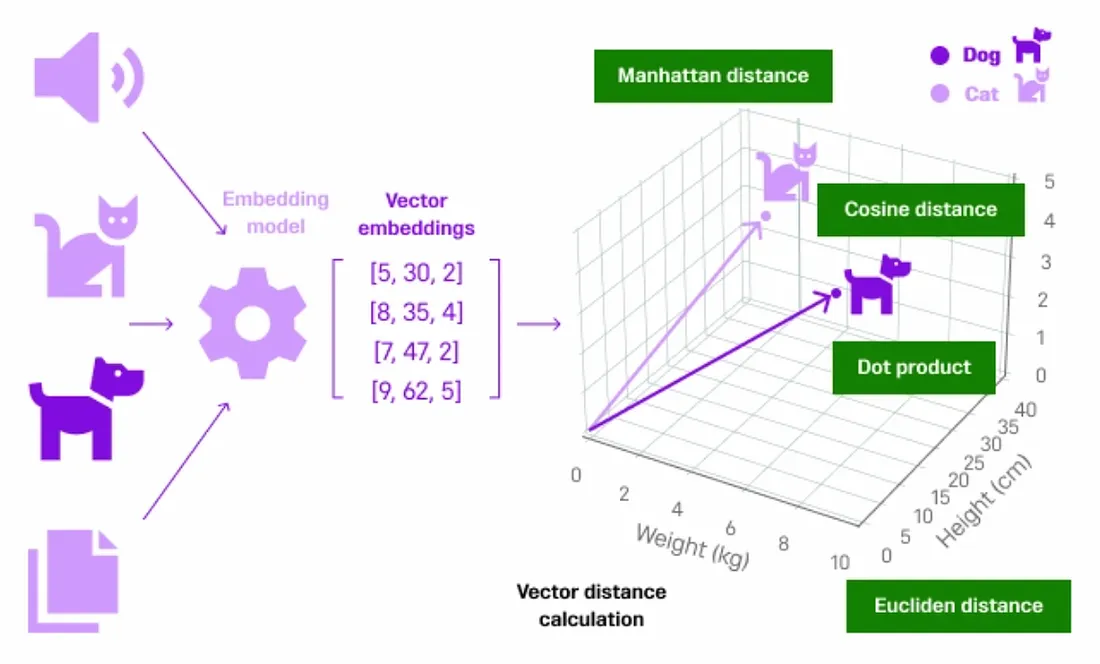
如上图所示，考虑来自不同来源的非结构化数据。数据通过嵌入模型（OpenAI、Cohere 或 HuggingFace 等）将内容转换成小的词块（向量嵌入）。每个词块都会分配一个数值，这个过程被称为标记化。创建完向量嵌入后，它们会在存储所有这些向量数据的向量数据库内的三维空间中表示出来。

在我们的案例中，如上图所示，非结构化数据 "猫 "和 "狗 "首先被转换为矢量数据，然后在三维空间中被表示为彼此更接近的数据，因为它们都属于同一个宠物类别。如果我们在这里再考虑一个 "汽车 "的例子，那么它的表示就会远离 "猫 "和 "狗"，因为它不属于宠物类别。

这样，相似的对象就会被放在一起，当用户进行查询时，就会考虑到上下文，并检索出更相似的对象返回给用户。

如何计算矢量相似性搜索

矢量之间的距离有不同的计算方法。Manhattan distance、 Euclidean distance、Cosine distance 和 dot product都是向量相似性搜索中使用的基本概念。每种方法都可以测量多维空间中两个向量之间的相似度。

Manhattan距离

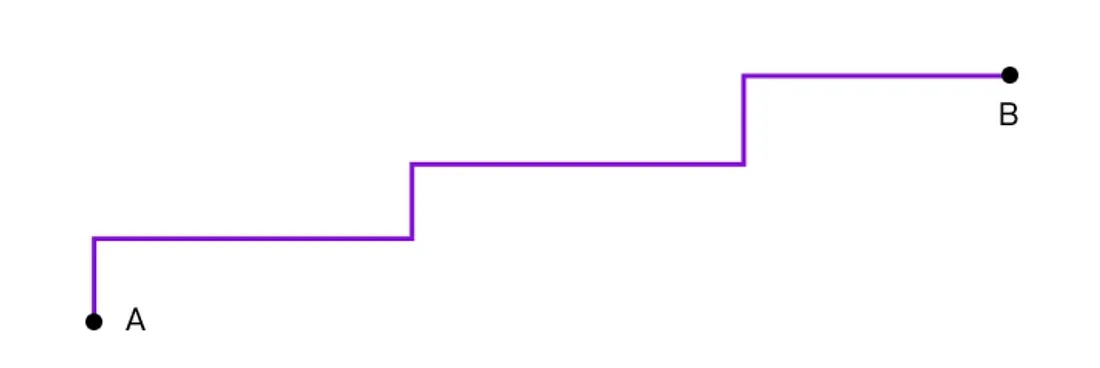
Manhattan距离是计算两点（矢量）之间距离的一种方法，方法是将两点坐标的绝对差值相加。想象一下在一个完美网格中的城市中航行：两点之间的Manhattan距离是指从一点到另一点所需的纵向和横向路程的总和，不可能走对角线捷径。矢量的情况也类似：将矢量中每个相应分量的绝对差值相加，即可计算出距离。

Euclidean距离

Euclidean距离通常被称为 L2 准则，是测量两点或向量间距离的最直接方法，类似于我们通常在物理世界中思考距离的方式。想象一下在地图上的两点之间画一条直线，Euclidean距离就是这条直线的长度。

这种度量方法被广泛应用于许多领域，包括物理学中的实际距离测量、机器学习算法中的聚类和分类等任务，以及日常场景中需要确定直接距离或咫尺之遥的距离时。它与我们对距离的直观理解自然吻合，因此成为数据分析和几何的基本工具。

Cosine距离

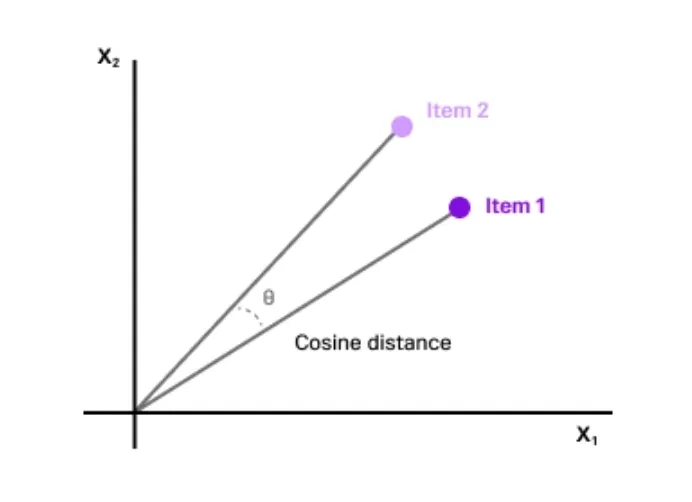
Cosine距离是两个非零向量之间相似性的度量，它评估的是两个向量之间角度的余弦。它不是传统意义上的 "距离"，而是一种度量，用于确定矢量之间的相对方向，而与矢量的大小无关。想象两个箭头从同一点出发，它们之间的夹角越小，方向就越相似。

这种测量方法在文本分析和信息检索等领域特别有用，因为在这些领域中，向量（例如代表高维空间中的文档或查询）的方向比它们的绝对位置或大小更重要。

dot product

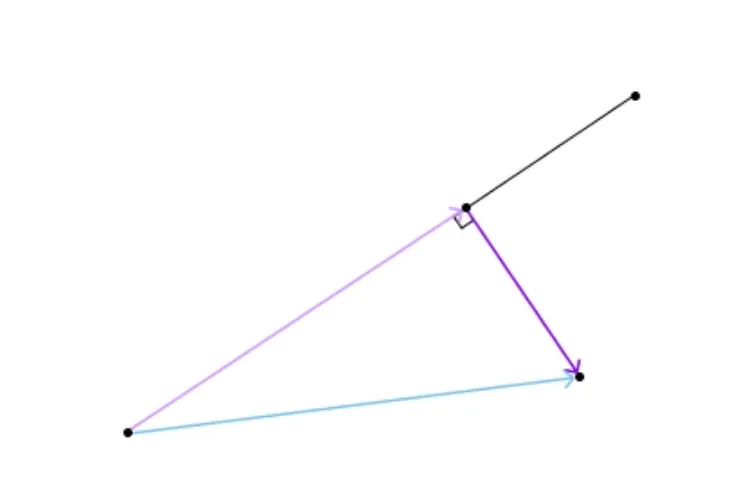
dot product反映了两个向量之间的关系。想象两个箭头从同一起点延伸出来，点积量化了一个箭头与另一个箭头方向的一致程度。在数学上，计算方法是将向量的相应分量相乘，然后将这些乘积相加。

dot product的一个主要特点是，当矢量指向相似或相反的方向时，点积较大（正或负），而当矢量垂直时，点积较小（或为零）。这使得点积在各种应用中都非常有用，例如确定两个向量是否正交、计算空间中向量之间的角度，或者在计算功或扭矩等更复杂的物理和工程操作中。在机器学习和数据科学中，点积在神经网络等算法中发挥着重要作用，有助于计算输入的加权和。

教程

我们将使用 SingleStore Notebooks 来执行本教程。如果还没有激活，请激活免费的 SingleStore 试用版开始学习。让我们通过实践教程深入了解前面提到的方法。

让我们以两只宠物（猫和狗）为例，在三维空间中将它们可视化。我们将尝试找出这两只宠物之间的曼哈顿距离、欧氏距离、余弦距离和点积（Manhattan distance, Euclidean distance, Cosine distance 和 dot product。）。

注册后，单击 "笔记本 "选项卡，创建一个带有名称的空白笔记本。

你可以开始在新创建的笔记本中运行代码。首先，安装并导入所需的库。

!pip install numpy
!pip install matplotlib
import matplotlib.pyplot as plt
import numpy as np

定义可在三维空间中表示的宠物属性。由于宠物是具有多种特征的复杂实体，你需要将其简化为三维表示。下面是一个例子：

from mpl_toolkits.mplot3d import Axes3D
# Example pets attributes: [weight, height, age]
# These are hypothetical numbers for illustration purposes
dog = [5, 30, 2]
cat = [3, 25, 4]
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
# Plotting the pets
ax.scatter(dog[0], dog[1], dog[2], label="Dog", c='blue')
ax.scatter(cat[0], cat[1], cat[2], label="Cat", c='green')
# Drawing lines from the origin to the points
ax.quiver(0, 0, 0, dog[0], dog[1], dog[2], color='blue',
arrow_length_ratio=0.1)
ax.quiver(0, 0, 0, cat[0], cat[1], cat[2], color='green', 
arrow_length_ratio=0.1)
# Labeling the axes
ax.set_xlabel('Weight (kg)')
ax.set_ylabel('Height (cm)')
ax.set_zlabel('Age (years)')
# Setting the limits for better visualization
ax.set_xlim(0, 10)
ax.set_ylim(0, 40)
ax.set_zlim(0, 5)
# Adding legend and title
ax.legend()
ax.set_title('3D Representation of Pets')
plt.show()

执行代码后，你将看到宠物在三维空间中的表现。

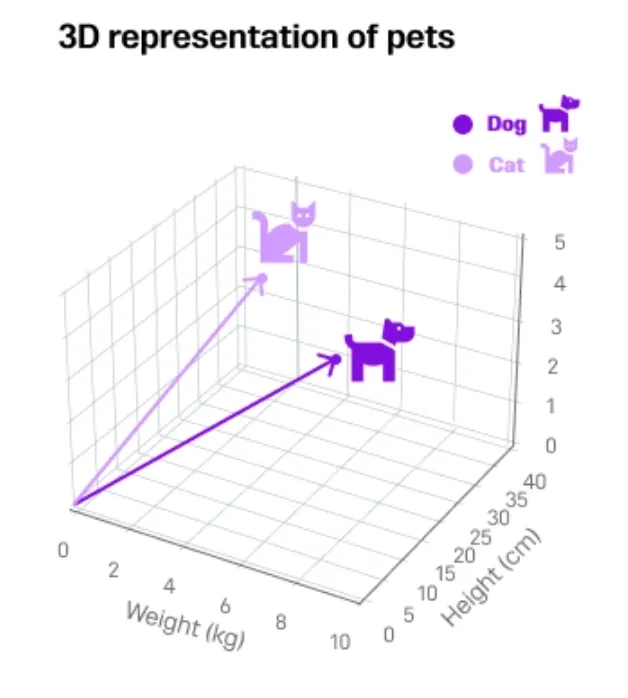
现在，让我们使用各种技术来计算向量之间的距离。

Manhattan距离

L1 = [abs(dog[i] - cat[i]) for i in range(len(dog))]abs(dog[i] - cat[i]) for i in range(len(dog))]
manhattan_distance = sum(L1)
print("Manhattan Distance:", manhattan_distance)

Euclidean距离

L2 = [(dog[i] - cat[i])**2 for i in range(len(dog))]2 for i in range(len(dog))]
L2 = np.sqrt(np.array(L2).sum())
print(L2)

Cosine距离

cosine = np.dot(dog, cat) / (np.linalg.norm(dog) * cat) / (np.linalg.norm(dog) * 
np.linalg.norm(cat))
print(cosine)

dot product

np.dot(dog,cat)cat)

DOT_PRODUCTSingleStore 分别使用向量函数和为点积和欧几里得距离提供直接支持EUCLIDEAN_DISTANCE。余弦相似度通过组合DOT_PRODUCT和SQRT函数来支持。

SingleStore 同时支持全文搜索和矢量搜索，为开发人员提供了两全其美的优势。SingleStore 的 8.5 版本更新打开了许多大门，在生成型 AI 领域掀起了巨大的浪潮。