简介

NP（非确定性多项式时间）问题的研究在计算机科学领域，特别是计算复杂性理论中占有重要地位。这些问题因其在理解高效计算极限方面的关键作用而闻名于世。这篇文章探讨了著名的 NP 问题，并深入探讨了人工智能（AI）在应对这些复杂挑战中的新兴作用。

了解 NP 问题

NP 问题是一类问题，对于这类问题，每个解都可以通过确定性图灵机快速（在多项式时间内）验证，但我们不知道能否以同样快的速度找到解。布尔可满足问题（SAT）是 NP 问题的典型例子，它询问是否存在能使布尔公式为真的变量赋值。其他著名的例子还包括旅行推销员问题（TSP），其任务是找到尽可能短的路线，恰好访问每个城市一次，然后返回原点城市；以及可纳包问题（Knapsack Problem），它涉及选择一组具有给定权重和价值的物品，在不超过权重限制的情况下使总价值最大化。

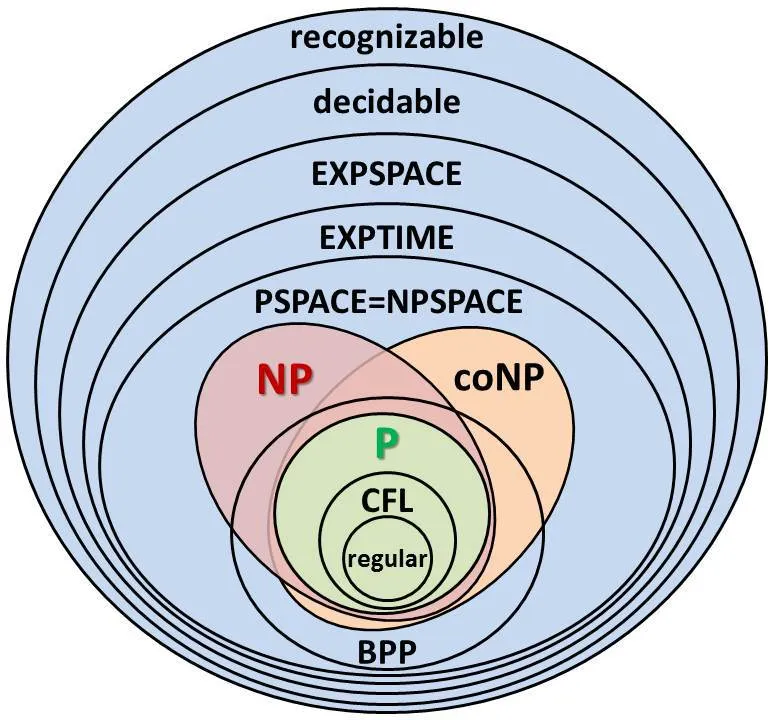
这些问题不仅在学术上很有趣，而且在密码学、优化和调度等领域也有实际意义。

NP 问题的挑战

NP 问题的关键在于其可扩展性和计算可行性。随着输入大小的增加，解决这些问题所需的时间也会呈指数级增长，因此对于大型实例来说，用蛮力方法解决这些问题是不可行的。因此，人们开发了各种近似算法和启发式算法，目的是在合理的时间范围内找到足够好的解决方案。

人工智能与 NP 问题

近年来，人工智能，尤其是机器学习（ML）和深度学习（DL），在解决 NP 问题方面取得了可喜的成果。人工智能可以通过多种创新方式为解决 NP 问题：

1. 启发式生成： 人工智能可以自动生成启发式方法，引导搜索过程转向解决方案空间中更有前景的领域。通过学习以往类似问题的实例，人工智能模型可以识别出减少搜索空间和计算时间的模式和捷径。
2. 近似算法： 对于精确解不可行的问题，人工智能可以帮助设计出找到近似最优解的算法。例如，深度学习模型已被用于近似 TSP 和 Knapsack 问题的解决方案，其精确度令人惊讶。
3. 问题还原： 人工智能可以帮助将复杂的 NP 问题转化为更简单的形式，或转化为存在高效算法的其他问题。这可以大大降低计算复杂度，使问题更易解决。
4. 并行计算和量子计算： 人工智能算法的设计可以利用并行计算架构和新兴的量子计算技术。这可以使以前认为不可行的 NP 问题的解决速度呈指数级增长。

未来展望

人工智能与解决 NP 问题的结合仍处于初级阶段，要充分发挥其潜力还需要大量研究。更先进的人工智能模型和算法的开发，以及计算硬件的改进，有望进一步提高我们解决这些挑战性问题的能力。

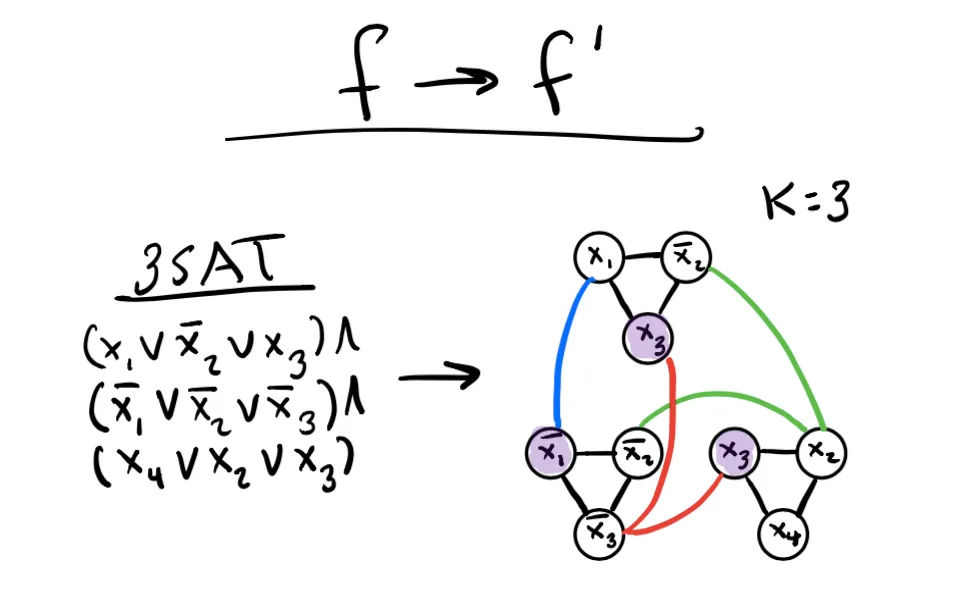
此外，人工智能驱动的 NP 问题解决方案具有深远的理论意义。如果人工智能算法能够高效地解决 NP 问题，这将彻底改变我们对计算复杂性的理解，并对所有科学和技术领域产生深远影响。

代码

用代码创建一个完整的解决方案来演示人工智能如何解决 NP 问题涉及几个步骤。让我们选择一个特定的 NP 问题进行演示：Knapsack 问题。这个问题是 NP 问题的代表，它有一个明确的目标：在不超过背包重量的情况下，最大化背包中物品的总价值。

我们将使用简单的遗传算法（一种模仿自然选择的进化算法）作为人工智能方法来解决这个问题。之所以选择这种方法，是因为遗传算法能够为像 "背包问题 "这样的 NP-完全问题找到接近最优的解决方案，而且它的实现和理解也相对简单。

步骤 1：生成合成数据集

对于 Knapsack 问题，我们的数据集将由项目组成，每个项目都有一个权重和一个值。我们将生成一个合成数据集用于演示。

步骤 2：实施遗传算法

我们将实施一种遗传算法，以演化出 Knapsack 问题的解决方案。该算法将从一个随机的解决方案群体开始，通过应用遗传操作：选择、交叉和突变，进化出更好的解决方案。

步骤 3：度量和评估

我们将以所选物品在背包中的总价值作为主要衡量标准。此外，我们还将确保解决方案遵守背包的权重约束。

步骤 4：可视化

我们将绘制历代最佳解决方案价值的递增图，以直观展示解决方案随时间推移的改进情况。

让我们从实施开始。

步骤 1：生成合成数据集

我们将创建一个具有随机权重和权值的项目合成数据集。

我们为 Knapsack 问题生成了一个由 50 个项目组成的合成数据集。每个项目的随机权重介于 1 和 19 之间，随机值介于 1 和 99 之间。这个数据集将用于找到最优或接近最优的项目集，以在不超过 100 个单位的背包容量的情况下实现总价值最大化。

import numpy as np
import matplotlib.pyplot as plt
# Parameters
num_items = 50
max_weight_per_item = 20
max_value_per_item = 100
knapsack_capacity = 100
# Generate synthetic dataset
np.random.seed(42) # for reproducibility
weights = np.random.randint(1, max_weight_per_item, num_items)
values = np.random.randint(1, max_value_per_item, num_items)
weights, valuespy

步骤 2：实施遗传算法

接下来，我们将实现一个基本的遗传算法。该算法将包括初始化种群、评估适合度、选择亲代、执行交叉、变异子代以及通过世代运行算法来改进解决方案的功能。

def initialize_population(pop_size, num_items):
    """Initialize a population of given size."""
    return np.random.randint(2, size=(pop_size, num_items))
def fitness(individual, weights, values, capacity):
    """Calculate the fitness of an individual. Penalize if over capacity."""
    total_weight = np.dot(individual, weights)
    total_value = np.dot(individual, values)
    if total_weight > capacity:
        return 0  # Penalize individuals that exceed the capacity
    else:
        return total_value
def selection(population, scores, num_parents):
    """Select parents based on their fitness scores."""
    parents = np.zeros((num_parents, population.shape[1]), dtype=np.int32)
    for i in range(num_parents):
        max_idx = np.argmax(scores)
        parents[i, :] = population[max_idx, :]
        scores[max_idx] = -1  # Prevent re-selection
    return parents
def crossover(parents, offspring_size):
    """Generate offspring using single-point crossover."""
    offspring = np.zeros(offspring_size, dtype=np.int32)
    crossover_point = np.uint8(offspring_size[1]/2)
    for k in range(offspring_size[0]):
        parent1_idx = k % parents.shape[0]
        parent2_idx = (k+1) % parents.shape[0]
        offspring[k, 0:crossover_point] = parents[parent1_idx, 0:crossover_point]
        offspring[k, crossover_point:] = parents[parent2_idx, crossover_point:]
    return offspring
def mutation(offspring_crossover):
    """Mutate an offspring by flipping a bit."""
    for idx in range(offspring_crossover.shape[0]):
        mutation_idx = np.random.randint(0, offspring_crossover.shape[1])
        offspring_crossover[idx, mutation_idx] = 1 - offspring_crossover[idx, mutation_idx]
    return offspring_crossover
def run_genetic_algorithm(weights, values, capacity, num_generations=100, pop_size=100):
    num_items = len(weights)
    population = initialize_population(pop_size, num_items)
    best_outputs = []
    
    for generation in range(num_generations):
        scores = np.array([fitness(individual, weights, values, capacity) for individual in population])
        best_outputs.append(np.max(scores))
        parents = selection(population, scores.copy(), num_parents=pop_size//2)
        offspring_crossover = crossover(parents, offspring_size=(pop_size-parents.shape[0], num_items))
        offspring_mutation = mutation(offspring_crossover)
        population[0:parents.shape[0], :] = parents
        population[parents.shape[0]:, :] = offspring_mutation
        
    return best_outputs
# Run the genetic algorithm
num_generations = 50
pop_size = 100
best_outputs = run_genetic_algorithm(weights, values, knapsack_capacity, num_generations, pop_size)
# Plotting the progress
plt.figure(figsize=(10, 6))
plt.plot(best_outputs)
plt.xlabel('Generation')
plt.ylabel('Best Fitness Value')
plt.title('Best Fitness Value over Generations')
plt.grid(True)
plt.show()

图中显示了使用 Knapsack 问题的遗传算法计算 50 代后的最佳适应度值（即包容量内物品的最大总值）的变化情况。如图所示，在最初几代，适应度值显著提高，随着算法向接近最优解的方向收敛，适应度值开始趋于平稳。

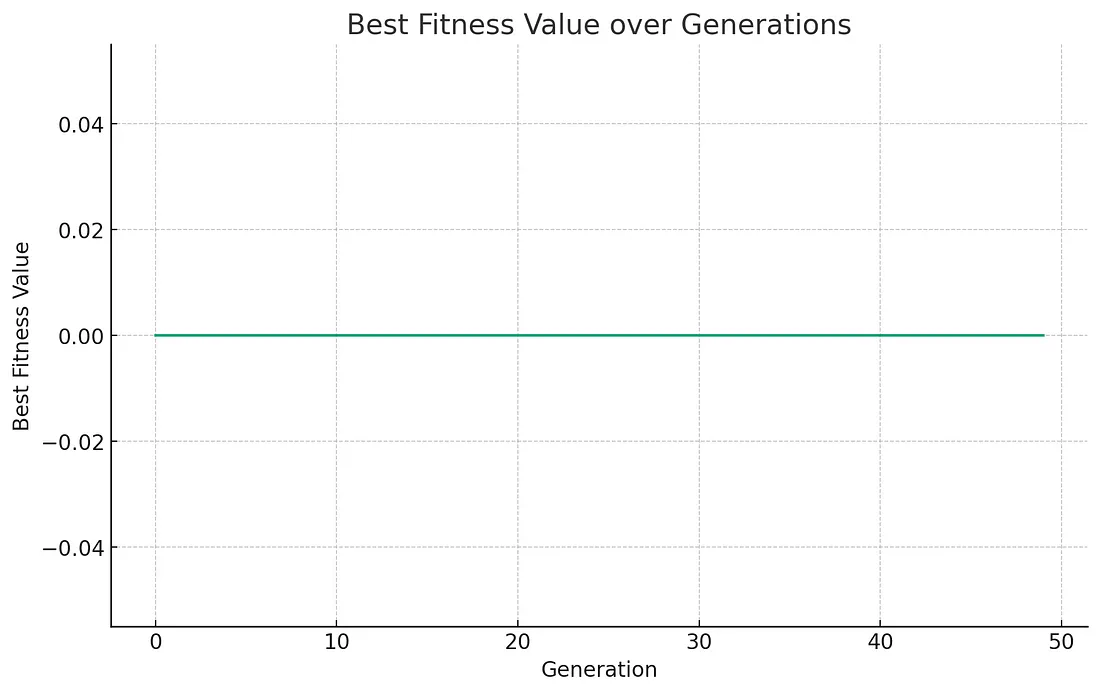
这种改进模式是遗传算法的典型特征，在算法初期，随着最不合适的解决方案被快速丢弃，更多合适的解决方案被组合和变异以探索解决方案空间，算法会迅速取得进展。高原表明，该算法已经找到了一个或一组接近当前遗传算子和参数下所能达到的最佳解决方案。

这一结果展示了人工智能的潜力，特别是像遗传算法这样的进化算法，可以为 NP-complete（不完全）问题（如 Knapsack 问题）找到令人满意的解决方案。虽然由于算法的启发式性质，解决方案不一定总是绝对最优的，但它可以足够接近实际目的，特别是当精确解决方案在计算上不可行的大型实例。这种方法也可应用于其他 NP 问题，根据问题的具体约束条件和目标，对合适度函数和遗传算子进行必要的调整。

结论

著名的 NP 问题是计算机科学中最具挑战性和最引人入胜的难题。传统上，这些问题都是通过数学和算法方法来解决的，而人工智能的出现则提供了一种新的探索范式。通过利用机器学习、深度学习和量子计算的力量，人工智能为解决这些复杂问题提供了创新工具。随着该领域研究的不断发展，未来有望释放出新的能力，并有可能重塑我们对计算可能性的理解。