当用户输入查询时，该过程涉及对用户查询进行标记并使用用于嵌入原始数据的相同模型来执行嵌入。随后，根据与用户查询的相似性，从知识库中提取相关块。

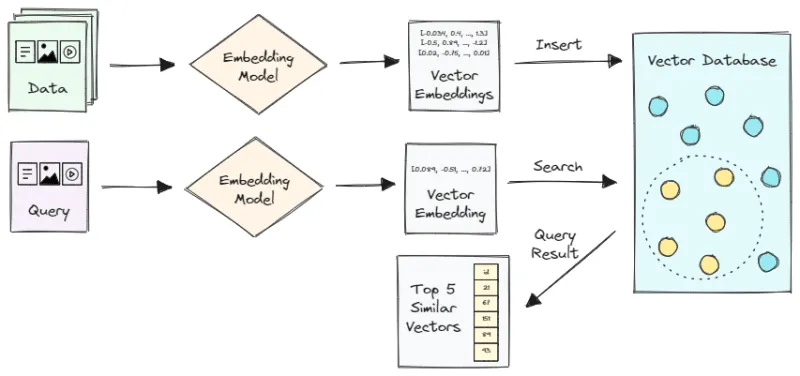
本文将全面探讨搜索过程的复杂性。下图显示了“搜索”在整个 RAG 管道中的具体位置。

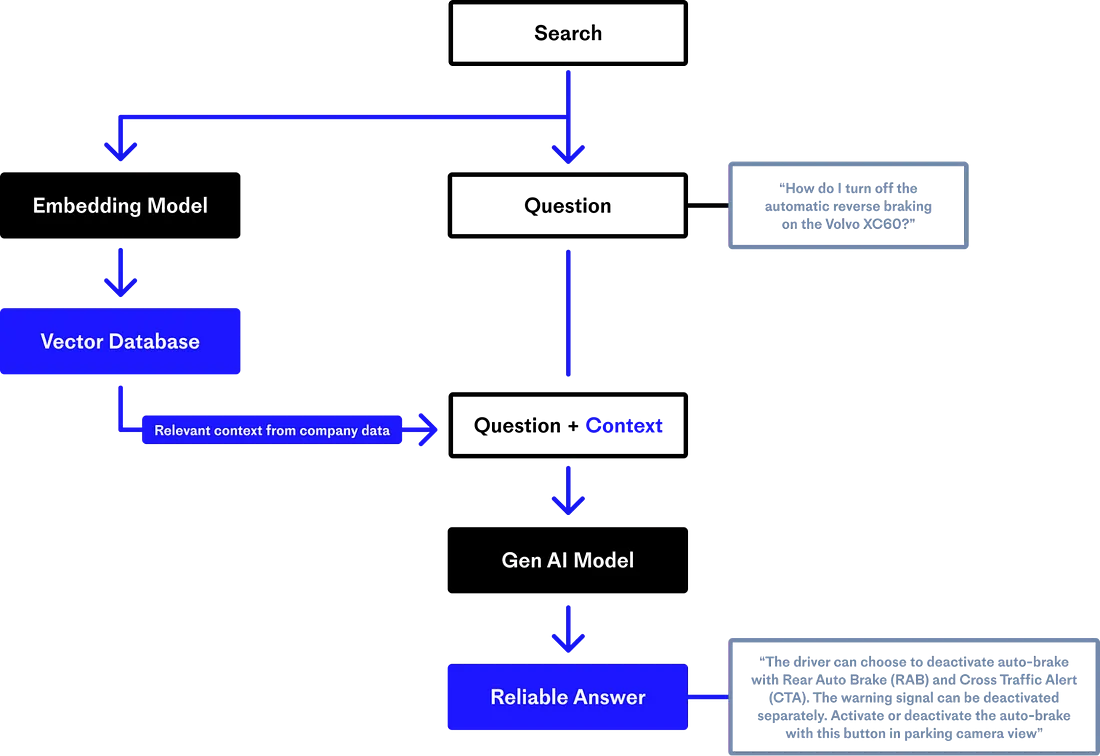
简介

让我们考虑一下使用 LLM 开发客户支持聊天机器人的常见场景。通常，团队会拥有大量的产品文档，其中包括大量非结构化数据，详细介绍了他们的产品、常见问题和使用案例。

这些数据通过一个称为 "分块 "的过程被分解成若干块。数据分解后，每个分块都会被分配一个唯一的标识符，并嵌入到矢量数据库的高维空间中。这一过程利用先进的自然语言处理技术来理解每个数据块的上下文和语义。

当客户提出问题时，LLM 会使用检索算法快速识别并从矢量数据库中获取最相关的信息块。这种检索是基于查询和语块之间的语义相似性，而不仅仅是关键词匹配。

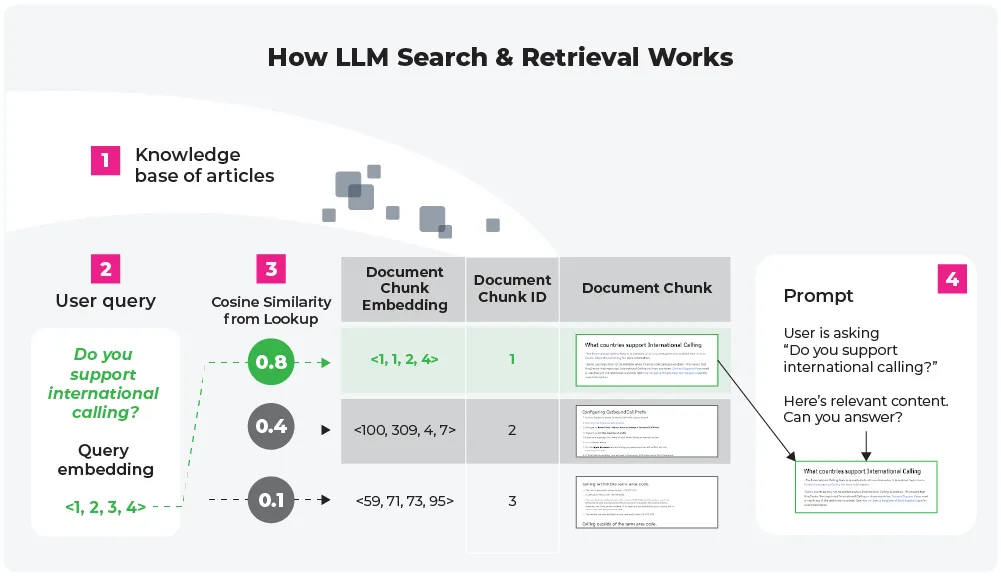
上图显示了搜索和检索如何与提示模板（上图中的 "4"）一起使用，以生成最终的 LLM 提示上下文。上图是搜索和检索 LLM 用例的最简单形式：文档被分割成若干块，这些块被嵌入到一个向量存储中，搜索和检索过程利用这个上下文来形成 LLM 输出。

这种方法有几个优点。首先，它大大减少了 LLM 处理大量数据所需的时间和计算资源，因为它只需要与相关的块进行交互，而不是与整个文档进行交互。

其次，它允许对数据库进行实时更新。随着产品文档的发展，矢量数据库中的相应块也可以轻松更新。这样就能确保聊天机器人始终提供最新信息。

最后，通过关注语义相关的信息块，LLM 可以提供更精确、更适合上下文的回复，从而提高客户满意度。

搜索和检索的问题

虽然搜索和检索方法大大提高了 LLM 的效率和准确性，但它也不是没有潜在的隐患。及早发现这些问题可以避免影响用户体验。

当用户输入的查询与矢量存储中的任何块不完全匹配时，就会出现这样的挑战。系统会大海捞针，但却一无所获。这种缺乏匹配的情况通常是由独特或高度特定的查询造成的，可能会让系统利用 "最相似 "的可用数据块--那些并不完全相关的数据块。

反过来，这又会导致 LLM 响应不佳。由于 LLM 依赖于数据块的相关性来生成响应，因此缺乏适当的匹配可能会导致输出与用户查询不相关甚至完全不相关的内容。

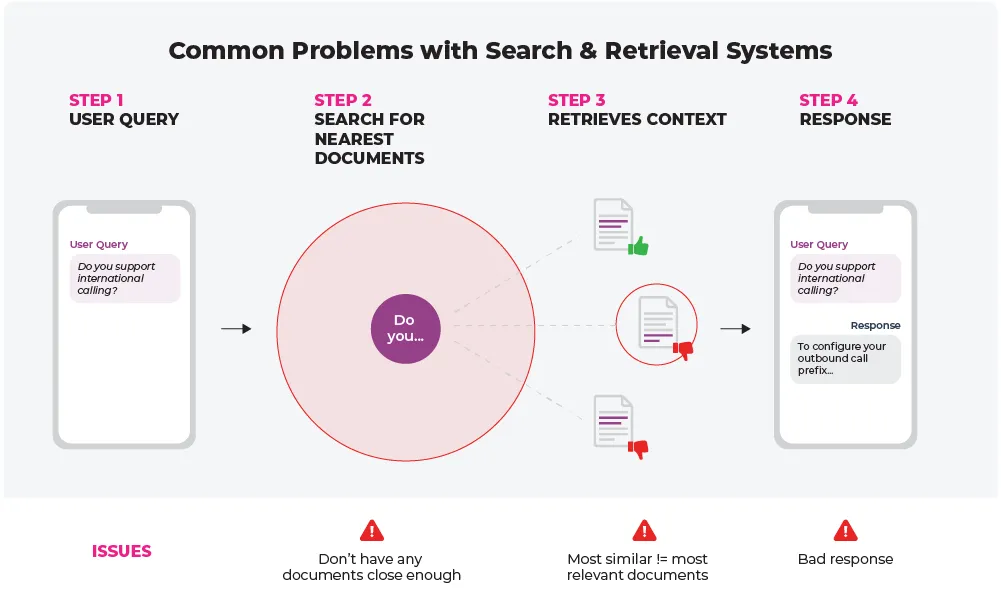
LLM 不相关或不合格的响应会让用户感到沮丧，降低他们的满意度，最终导致他们对整个系统和产品失去信任。

监控三个主要方面有助于防止这些问题的发生：

查询密度（漂移）： 查询密度是指向量存储对用户查询的覆盖程度。如果查询密度大幅漂移，则表明我们的矢量存储可能无法捕获全部的用户查询，从而导致缺少密切相关的数据块。定期监控查询密度能让我们发现这些差距或不足。有了这种洞察力，我们就可以通过纳入更多相关的数据块或改进现有数据块来增强矢量存储，从而提高系统获取数据以响应用户查询的能力。

排名指标： 这些指标用于评估搜索和检索系统在选择最相关数据块方面的表现。如果排名指标显示性能下降，则表明系统区分相关和不相关数据块的能力可能需要改进。

用户反馈： 鼓励用户就 LLM 响应的质量和相关性提供反馈意见，有助于衡量用户满意度并确定需要改进的地方。对这些反馈进行定期分析可以指出模式和趋势，然后根据需要对应用程序进行调整。

优化搜索和检索

从构建阶段到后期制作，优化搜索和检索流程应贯穿于由 LLM 驱动的应用程序的整个生命周期。

在构建阶段，应注意制定稳健的测试和评估策略。通过这种方法，我们可以及早发现潜在问题并优化策略，为系统奠定坚实的基础。

需要关注的关键领域包括：

• 分块策略： 在这一阶段对信息的分解和处理方式进行评估，有助于突出需要改进的性能领域。
• 检索性能： 评估系统检索信息的性能可以表明我们是否需要采用不同的工具或策略，如上下文排序或 HYDE。

系统发布后，随着进入后期制作阶段，优化工作应继续进行。即使在发布之后，有了明确的评估策略，我们也可以主动发现任何新出现的问题，并继续改进模型的性能。请考虑以下方法：

• 扩展我们的知识库： 添加文档可以大大提高我们系统的响应质量。扩充数据集可使我们的 LLM 提供更准确、更有针对性的回复。
• 完善分块策略： 进一步修改信息分解和处理的方式可以带来明显的改进。
• 加强语境理解： 加入额外的 "上下文评估 "步骤有助于系统将最相关的上下文纳入 LLM 的回复中。

搜索类型

我们必须记住，矢量数据库并不是搜索的灵丹妙药--它们在语义搜索方面非常出色，但在许多情况下，传统的关键字搜索可以产生更多相关结果，并提高用户满意度。为什么会这样呢？这主要是因为基于余弦相似度等指标的排序会导致相似度得分较高的结果出现在可能包含特定输入关键词的部分匹配结果之上，从而降低了这些结果与最终用户的相关性。

然而，纯粹的关键字搜索也有其局限性--如果用户输入的术语在语义上与存储的数据相似（但并不精确），那么可能有用的相关结果就不会返回。由于这种权衡，现实世界中的搜索和检索用例需要结合关键词和矢量搜索，而矢量数据库是其中的关键组成部分（因为矢量数据库包含嵌入，可以进行语义相似性搜索，并能扩展到非常大的数据集）。

总结上述要点：

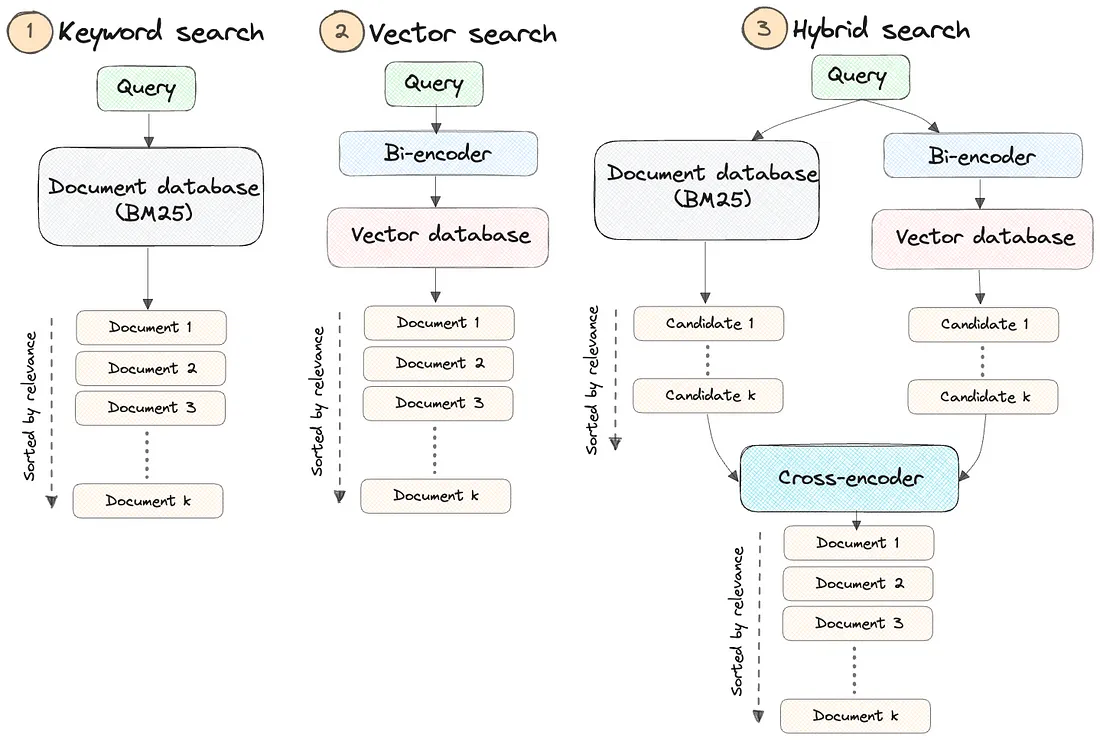
• 关键词搜索： 当用户知道自己在寻找什么，并希望搜索结果与其搜索词中的精确短语相匹配时，就能找到相关的有用结果。不需要矢量数据库。
• 矢量搜索： 当用户不知道他们到底在找什么时，可以找到相关的结果。需要矢量数据库。
• 混合（关键词+矢量）搜索： 通常结合全文关键词搜索和矢量搜索的候选结果，并使用交叉编码器模型对其重新排序。需要文档数据库和矢量数据库。

这可以通过下图有效地直观显示出来：

语义搜索

语义搜索旨在通过理解搜索查询的内容来提高搜索的准确性。与传统搜索引擎只根据词性匹配查找文件不同，语义搜索还能查找同义词。

搜索背景

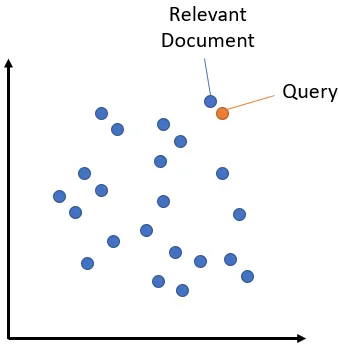
语义搜索背后的理念是将语料库中的所有条目（无论是句子、段落还是文档）嵌入到向量空间中。

在搜索时，查询会被嵌入到相同的向量空间中，并从我们的语料库中找到最接近的嵌入。这些条目应与查询语义高度重合。

对称语义搜索与非对称语义搜索

对称语义搜索与非对称语义搜索是我们设置的一个关键区别：

• 对于对称语义搜索，我们的查询和语料库中的条目长度大致相同，内容数量也相同。搜索类似问题就是一个例子： 例如，我们的查询可能是 "如何在线学习 Python？"，而我们想要找到的条目是 "如何在网络上学习 Python？"。对于对称任务，我们可能会翻转语料库中的查询和条目。
• 对于非对称语义搜索，我们通常会有一个简短的查询（如一个问题或一些关键词），而我们希望找到一个较长的段落来回答该查询。例如，我们有一个类似于 "Python 是什么 "的查询，而我们想找到的段落是 "Python 是一种解释型的高级通用编程语言。Python 的设计理念......"。对于非对称任务，翻转查询和语料库中的条目通常没有意义。

检索算法

相似性搜索（Vanilla Search）和最大边际相关性（MMR）

在检索文档时，大多数方法都会使用相似度指标，如余弦相似度、欧氏距离或点积。所有这些方法都会返回与我们的查询/问题最相似的文档。

但是，如果我们想要的相似文档之间也存在差异，该怎么办呢？这就是最大边际相关性（MMR）的作用所在。

这样做的目的是在决定返回哪些文档时，考虑到检索文档之间的相似程度。从理论上讲，我们应该拥有一组全面、多样的文档。

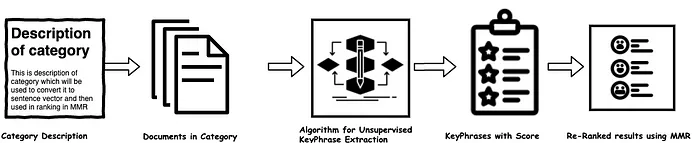
在无监督学习的情况下，假设我们的最终关键短语的排名是这样的Good Product, Great Product, Nice Product, Excellent Product, Easy Install, Nice UI, Light weight etc.，但这种方法存在一个问题，所有的短语good product, nice product, excellent product都是相似的，并且定义了产品的相同属性，并且排名较高。假设我们有一个空间只能显示 5 个关键短语，在这种情况下，我们不想显示所有这些相似的短语。

我们要妥善利用这个有限的空间，使关键短语显示的文档信息足够多样化。相似类型的短语不应占据整个空间，用户可以看到有关文档的各种信息。

1. 使用余弦相似性去除冗余短语
2. 使用 MMR 对关键短语重新排序

以上是两种广泛使用的检索方法。其他方法包括多查询检索、长上下文重排序、多矢量检索器、父文档检索器、自查询、时间加权矢量存储检索等。

现在，让我们讨论下面的检索和重新排序管道，看看它是如何增强结果的。

检索和重新排名

在语义搜索（Semantic Search）中，我们已经展示了如何使用句子转换器（Sentence Transformer）来计算查询、句子和段落的嵌入，以及如何将其用于语义搜索。

对于复杂的搜索任务，例如问题解答检索，使用Retrieve & Re-Rank可以大大提高搜索效率。

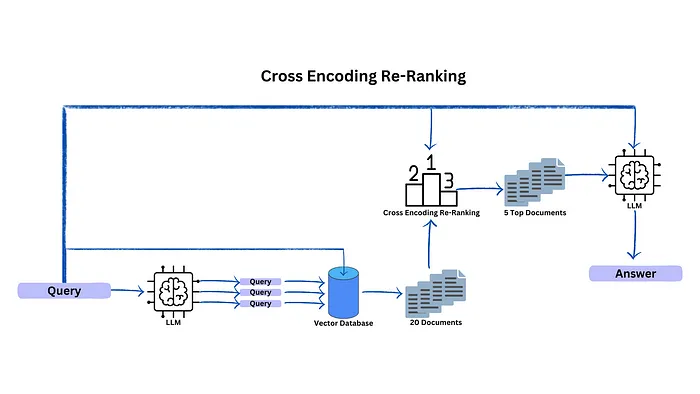
检索和重新排名管道

用于信息检索/问题解答检索的管道运行良好，如下所示。本文提供并解释了所有组件：

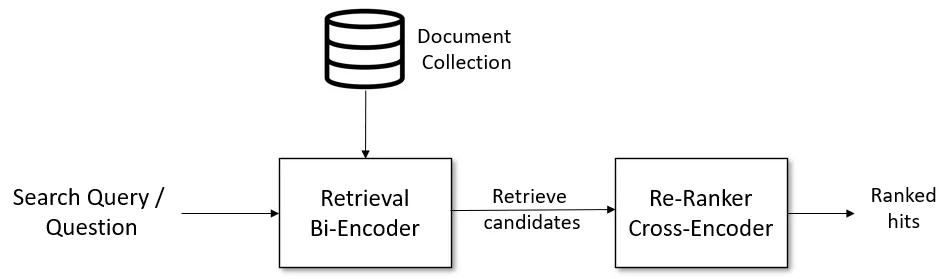
给定一个搜索查询，我们首先使用一个检索系统，检索出一个包含大量可能与查询相关的点击（例如 100 个）的列表。在检索过程中，我们可以使用词法搜索（例如 ElasticSearch），也可以使用双编码器进行密集检索。

不过，检索系统可能会检索到与搜索查询不那么相关的文档。因此，在第二阶段，我们使用基于交叉编码器的重新排序器，对给定搜索查询的所有候选文档的相关性进行评分。

输出结果将是一个经过排序的点击列表，我们可以将其呈现给用户。

检索： 双编码器

词法搜索在文档集中查找与查询词字面匹配的词。它不会识别同义词、缩略词或拼写变化。与此相反，语义搜索（或密集检索）将搜索查询编码到矢量空间，并检索在矢量空间中接近的文档嵌入。

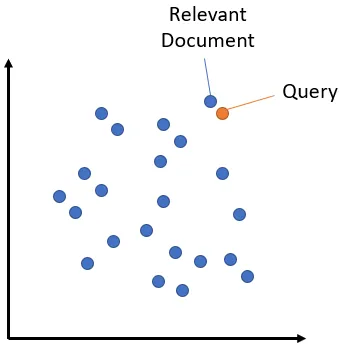
语义搜索克服了词法搜索的缺点，可以识别同义词和缩略词。

重新排名器 交叉编码器

对于拥有数百万词条的大型文档集来说，检索器必须是高效的。但是，它可能会返回不相关的候选条目。

基于交叉编码器的重新排序器可以大大改善用户的最终结果。查询和可能的文档同时传递给转换器网络，然后转换器网络输出一个介于 0 和 1 之间的分数，表示文档与给定查询的相关程度。

交叉编码器的优势在于性能更高，因为它们会对查询和文档进行关注。

对数以千计或数以百万计的（查询、文档）对进行评分的速度会相当慢。因此，我们使用检索器来创建一组候选词，例如 100 个可能的候选词，然后由交叉编码器重新排序。

脚本示例

• retrieve_rerank_simple_wikipedia.ipynb [ Colab 版本 ]： 该脚本使用较小的简单英语维基百科作为文档集，为用户的问题/搜索查询提供答案。首先，我们将所有维基百科文章分割成段落，并用双编码器对其进行编码。如果输入一个新的查询/问题，它将由相同的双编码器编码，并检索出余弦相似度最高的段落（见语义搜索）。接下来，检索到的候选段落由交叉编码器重新排序器进行评分，并将交叉编码器评分最高的 5 个段落呈现给用户。
• in_document_search_crossencoder.py： 如果只有一小部分段落，我们就不需要检索阶段。例如，如果我们想在单个文档中进行搜索，就会出现这种情况。在这个例子中，我们将维基百科中关于欧洲的文章分割成若干段落。然后，使用 Cross-Encoder 重排器对搜索查询/问题和所有段落进行评分。与查询最相关的段落将被返回。

预先训练的双编码器（检索）

双编码器能为我们的段落和搜索查询独立生成嵌入。我们可以这样使用它

from sentence_transformers import SentenceTransformer
model = SentenceTransformer('model_name')
docs = ["My first paragraph. That contains information", "Python is a programming language."]
document_embeddings = model.encode(docs)
query = "What is Python?"
query_embedding = model.encode(query)

信息检索评估

信息检索（IR）系统的评估对于做出明智的设计决策至关重要。从搜索到推荐，评估措施对于了解检索中哪些有效、哪些无效至关重要。

信息检索系统的评估指标可分为两类：在线或离线指标。

在线指标是在实际使用IR系统时获取的。这些指标考虑的是用户互动，如用户是否点击了 Netflix 推荐的节目，或是否点击了电子邮件广告中的特定链接（点击率或 CTR）。在线指标有很多，但它们都与某种形式的用户互动有关。

离线指标是在部署新的 IR 系统之前，在一个孤立的环境中进行测量的。这些指标考察的是在使用系统检索项目时，是否会返回一组特定的相关结果。

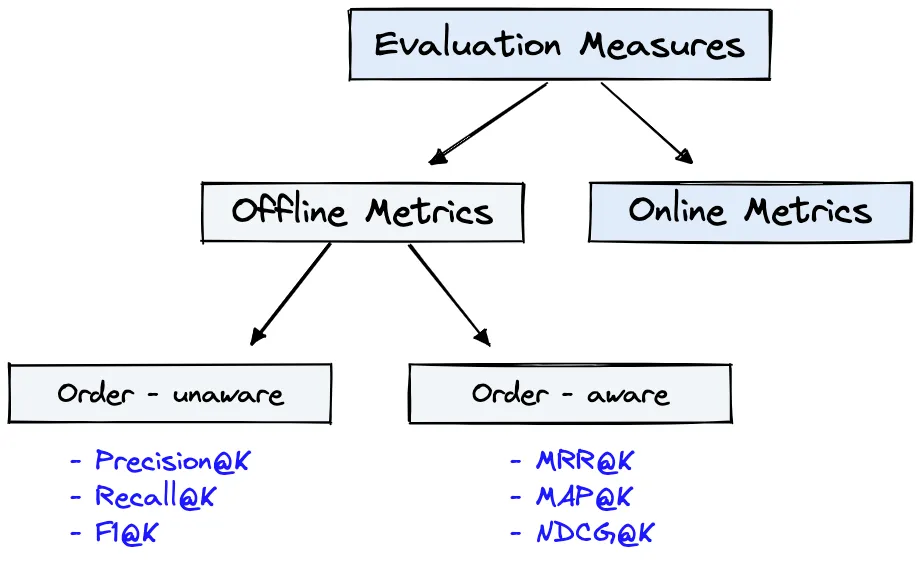
评估指标可分为离线指标和在线指标。离线度量指标又可分为顺序不感知（order-unaware）和顺序感知（order-aware）两种，我们很快会对此进行解释。

企业通常会同时使用离线和在线指标来衡量其 IR 系统的性能。不过，在部署之前，首先要使用离线指标来预测系统的性能。

我们将重点介绍最有用、最流行的离线指标：

• Recall@K
• 平均互易等级 (MRR)
• 平均精度@K (MAP@K)
• 归一化折现累积增益 (NDCG@K)

这些指标看似简单，却能让我们深入了解IR系统的性能。

我们可以在不同的评估阶段使用其中的一个或多个指标。在 Spotify 的播客搜索开发过程中，Recall@K（使用 K=1）被用于 "评估批次 "的训练，而在训练之后，Recall@K 和 MRR（使用 K=30）被用于更大的评估集。

现在，我们可以理解 Spotify 能够在向客户部署任何东西之前预测系统性能。这使他们能够成功部署 A/B 测试并显著提高播客参与度。

我们对这些指标还有两个细分：顺序感知和顺序非感知。这是指结果的顺序是否会影响指标得分。如果会，则该指标为顺序感知指标。否则，它就是不感知顺序的。

示例

在整篇文章中，我们将使用一个非常小的数据集，即 8 幅图像。实际上，这个数字很可能是数百万甚至更多。

如果我们搜索 "cat in a box"，可能会得到类似上面的结果。数字代表IR系统预测的每张图片的相关性排名。其他查询会产生不同顺序的结果。

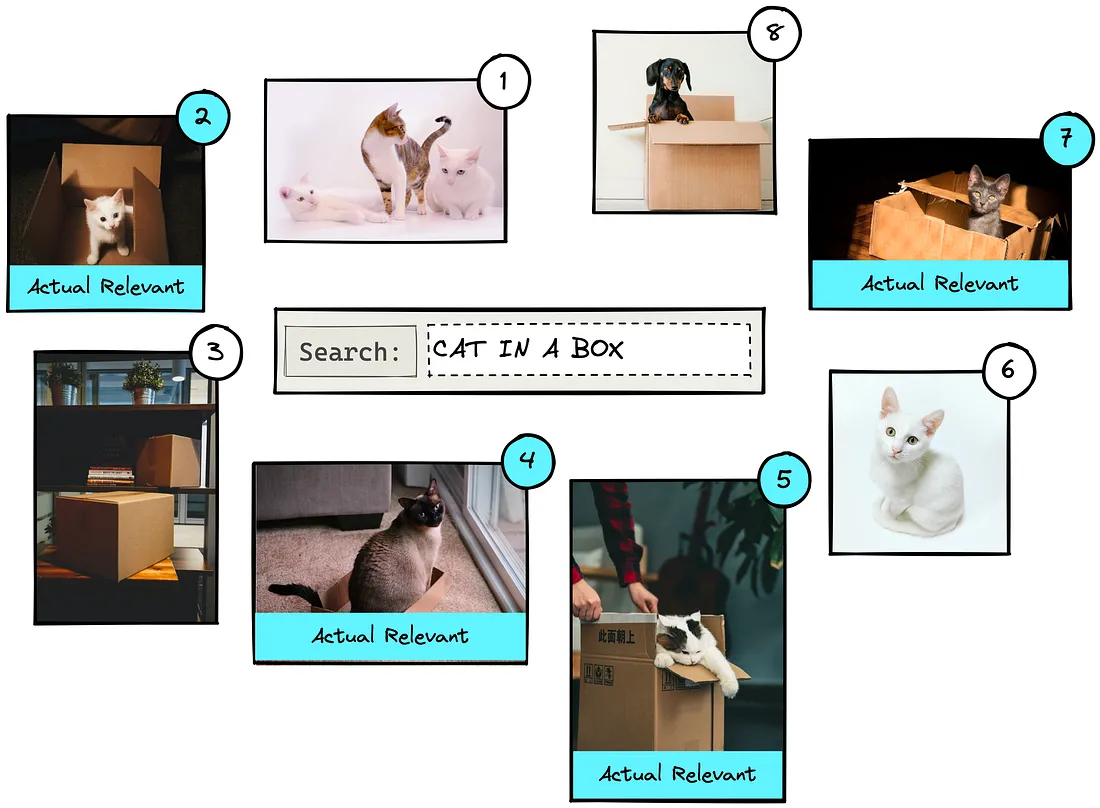
我们可以看到，结果 2、4、5 和 7 是实际相关的结果。其他结果则不相关，因为它们显示的是没有盒子的猫、没有猫的盒子或一只狗。

实际结果与预测结果

在评估IR系统的性能时，我们将比较实际条件和预测条件，其中，实际条件是指IR图像的真实标签：

• 实际条件是指数据集中每个项目的真实标签。如果项目与查询相关，则标签为正 (p)；如果项目与查询无关，则标签为负 (n)。
• 预测条件是 IR 系统返回的预测标签。如果一个条目被返回，则预测为正标签 (p^)；如果没有被返回，则预测为负标签 (n^)。

根据这些实际和预测条件，我们创建了一组输出，并据此计算所有离线指标。这就是真/假阳性结果和真/假阴性结果。

正面结果关注的是IR系统返回的结果。鉴于我们的数据集，我们要求IR系统使用 "cat in a box "查询返回两个条目。如果返回的是实际相关的结果，则为真阳性 (pp^)；如果返回的是不相关的结果，则为假阳性 (np^)。

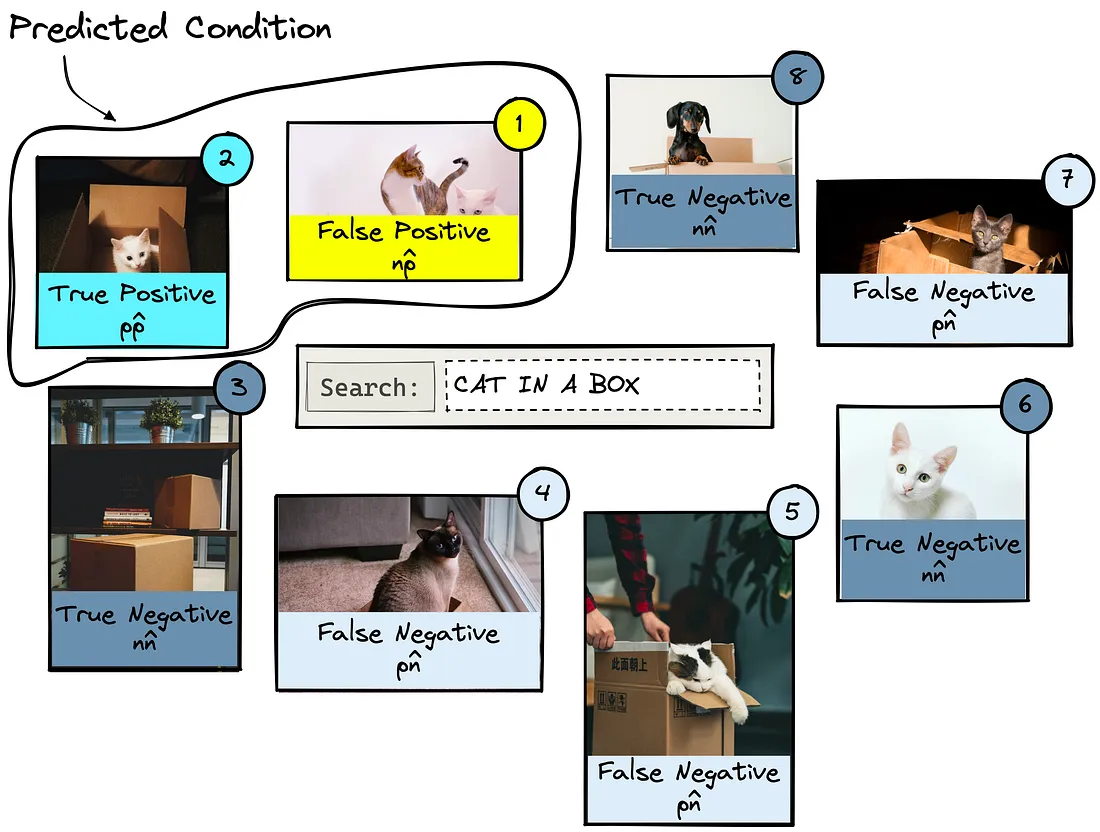
对于负结果，我们必须看看 IR 系统没有返回什么。让我们查询两个结果。任何相关但未返回的结果都是假负结果 (pn^)。没有返回的不相关项是真否定项 (nn^)。

考虑到这一点，我们可以从第一个指标开始。

Recall@K

Recall@K 是最易解释、最受欢迎的离线评估指标之一。它衡量的是有多少相关项目被返回（pp^），而整个数据集中又有多少相关项目（pp^+pn^）。

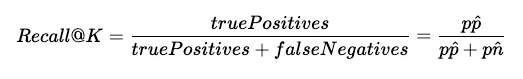
本指标和所有其他离线指标中的 K 指的是IR系统返回的条目的数量。在我们的例子中，整个数据集中共有 N = 8 个条目，因此 K 可以是 [1 ,..., N] 之间的任意值。

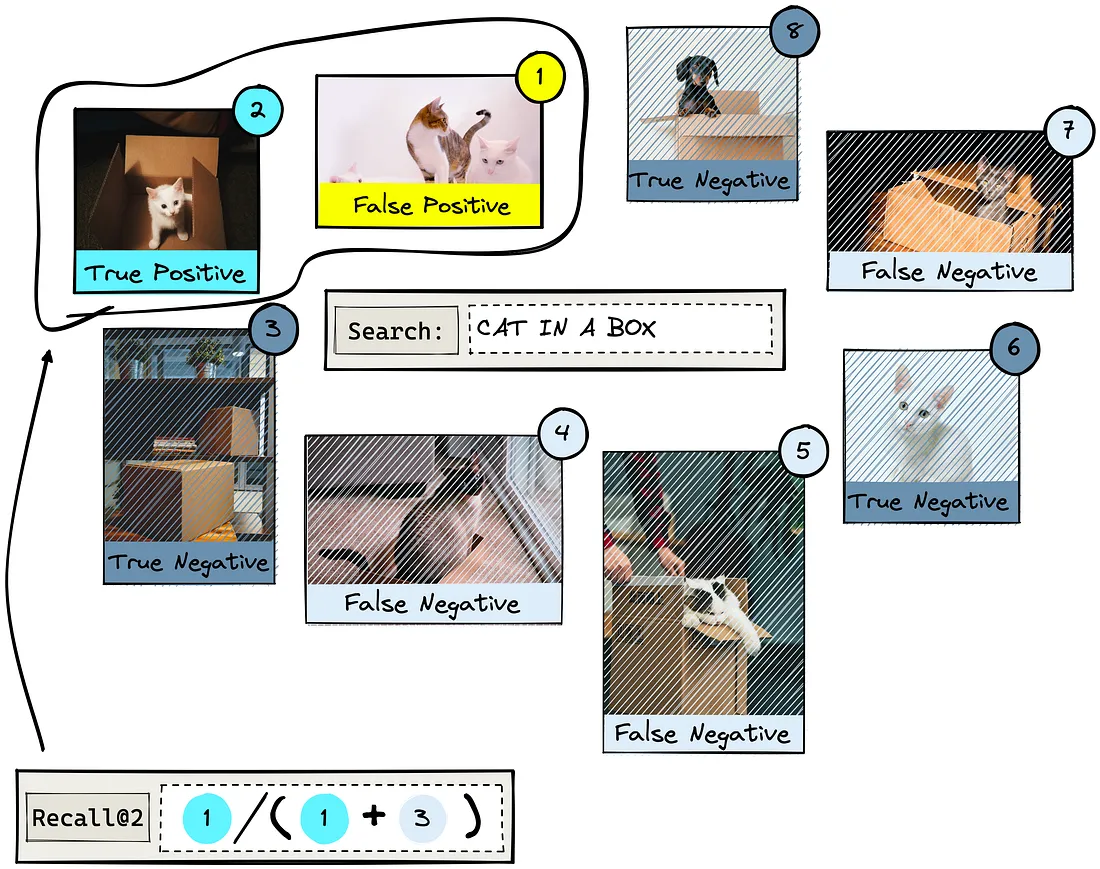
当 K = 2 时，我们的Recall@K 分数是以返回的相关结果数与整个数据集中的相关结果总数之比来计算的。也就是说:

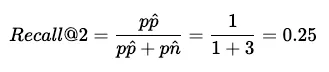
在Recall@K的情况下，随着 K 的增加和返回项目范围的扩大，得分也会提高。

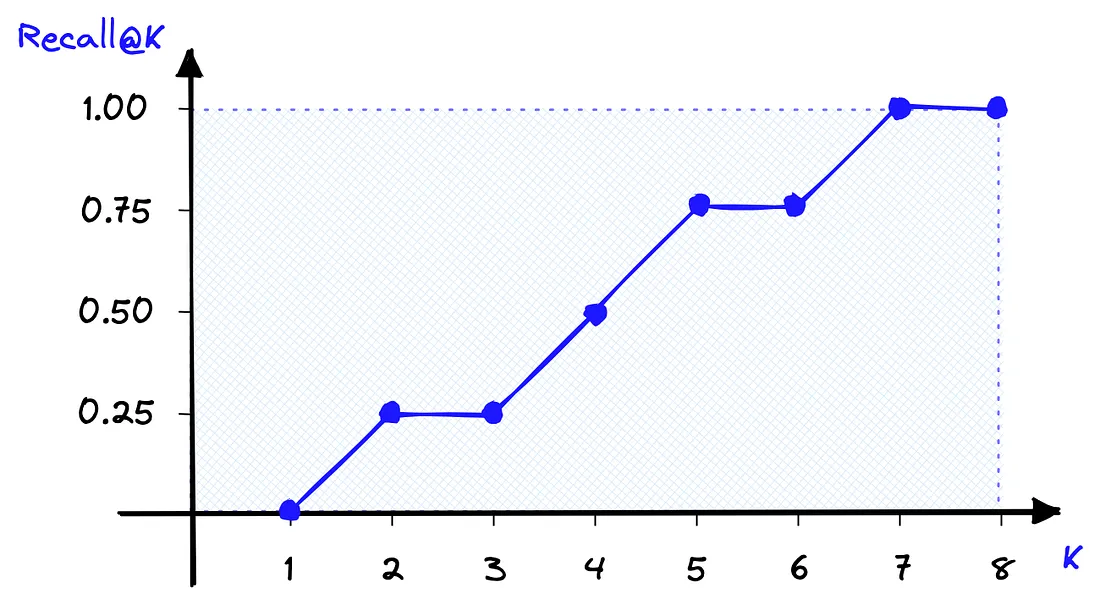
我们可以在 Python 中轻松计算出相同的 recall@K 分数。为此，我们将定义一个名为 recall 的函数，该函数接收实际条件和预测条件列表以及 K 值，并返回 recall@K 分数。

# recall@k function
def recall(actual, predicted, k):
    act_set = set(actual)
    pred_set = set(predicted[:k])
    result = round(len(act_set & pred_set) / float(len(act_set)), 2)
    return result

利用这一点，我们将在排名第 2、4、5 和 7 位复制我们的八张图片数据集，并在其中加入实际的相关结果。

actual = ["2", "4", "5", "7"]
predicted = ["1", "2", "3", "4", "5", "6", "7", "8"]
for k in range(1, 9):
    print(f"Recall@{k} = {recall(actual, predicted, k)}")

输出：

Recall@1 = 0.0
Recall@2 = 0.25
Recall@3 = 0.25
Recall@4 = 0.5
Recall@5 = 0.75
Recall@6 = 0.75
Recall@7 = 1.0
Recall@8 = 1.0

优点与缺点

Recall@K 无疑是最容易解释的评价指标之一。我们知道，满分表示所有相关项目都被返回。我们还知道，k 值越小，IR系统就越难在Recall@K 上取得好成绩。

不过，使用Recall@K也有缺点。通过将 K 值增加到 N 或接近 N，我们可以每次都返回满分，因此仅仅依靠 recall@K 可能会有欺骗性。

另一个问题是，它是一个不考虑顺序的指标。这意味着，如果我们使用Recall@4，并在排名第一时返回一个相关结果，我们的得分与在排名第四时返回相同结果的得分是一样的。显然，在更高的排序上返回实际相关的结果会更好，但Recall@K 无法解释这一点。

平均互易等级(MRR)

平均互易等级 (MRR) 是一个顺序感知指标，这意味着与Recall@K不同，在排名第一时返回实际相关结果比在排名第四时返回实际相关结果得分更高。

MRR 的另一个不同之处在于，它是根据多个查询计算得出的。其计算公式为:

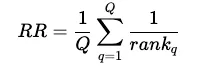
Q 是查询次数，q 是特定查询，rank-q 是查询 q 的第一个 * 实际相关 * 结果的排名。我们将逐步解释该公式。

在上一个例子中，用户搜索 "cat in a box"。我们再添加两个查询，得出 Q=3。

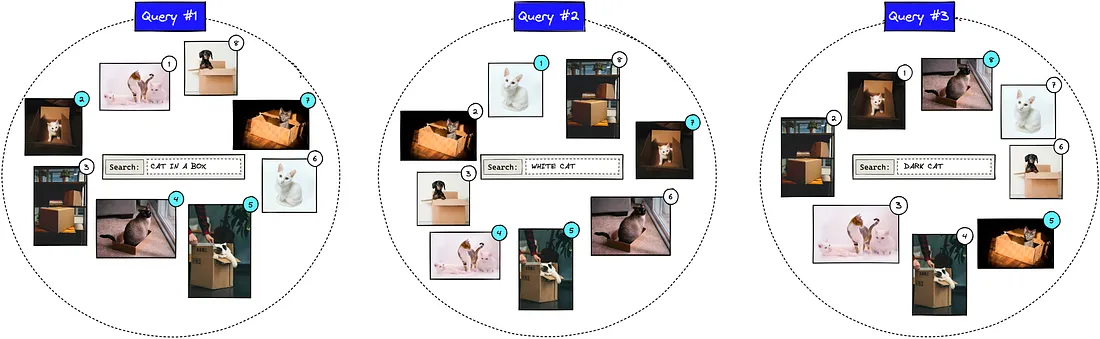
我们计算每个查询 q 的排名倒数 1/rankq。对于第一个查询，第一张实际相关图片会在第二位置返回，因此排名倒数为 1/2。我们来计算所有查询的排名倒数：

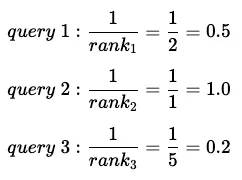
接下来，我们将查询 q=[1,...,Q]（例如，我们的三个查询）的所有倒数排名相加：

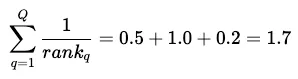
由于我们计算的是平均互易排名 (MRR)，因此必须用总互易排名除以查询次数 Q，得出平均值：

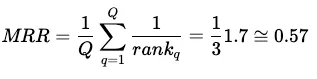
现在，让我们将其转换为 Python 语言。我们将使用相同的实际相关结果，复制 Q=3 的相同场景。

# relevant results for query #1, #2, and #3
actual_relevant = [
    [2, 4, 5, 7],
    [1, 4, 5, 7],
    [5, 8]
]

# number of queries
Q = len(actual_relevant)
# calculate the reciprocal of the first actual relevant rank
cumulative_reciprocal = 0
for i in range(Q):
    first_result = actual_relevant[i][0]
    reciprocal = 1 / first_result
    cumulative_reciprocal += reciprocal
    print(f"query #{i+1} = 1/{first_result} = {reciprocal}")
# calculate mrr
mrr = 1/Q * cumulative_reciprocal
# generate results
print("MRR =", round(mrr,2))

输出：

query #1 = 1/2 = 0.5
query #2 = 1/1 = 1.0
query #3 = 1/5 = 0.2
MRR = 0.57

不出所料，我们计算出的 MRR 分数同样为 0.57。

优缺点

MRR 有自己独特的优缺点。它是顺序感知的，这对于第一个相关结果的排名非常重要的使用案例（如聊天机器人或问题解答）来说是一个巨大的优势。

另一方面，我们只考虑第一个相关项的排名，而不考虑其他项。这意味着，对于我们希望返回多个项目（如推荐或搜索引擎）的使用案例，MRR 并不是一个好的衡量标准。例如，如果我们想向用户推荐 ~10 种产品，我们会要求 IR 系统检索 10 个条目。我们可以只返回排名第一的一个实际相关项目，而不返回其他相关项目。十个不相关的项目中有九个是很糟糕的结果，但 MRR 却能得到完美的 1.0 分。

另一个小缺点是，与Recall@K这样的简单指标相比，MRR 的可解释性较差。不过，与许多其他评价指标相比，它仍然更容易解释。

平均精确度 (MAP)

Mean Average Precision@K (MAP@K) 是另一种流行的顺序感知指标。起初，它的名字似乎有点奇怪，平均值的平均值？这是有道理的，我们保证。

计算 MAP@K 有几个步骤。我们先从另一个称为精确度@K 的指标开始：

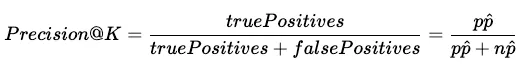
你可能会觉得这看起来与 recall@K 非常相似，的确如此！唯一不同的是，我们将召回中的 pn^ 换成了 np^。这意味着我们现在只考虑返回项中的实际相关结果和非相关结果。使用 precision@K 时，我们不考虑非返回项。

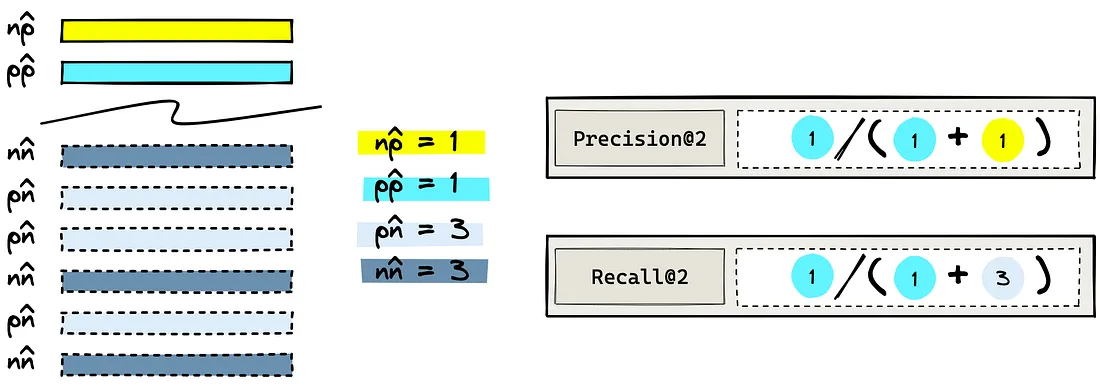
让我们回到 "cat in a box "的例子。我们将返回 ?=2K=2 个项目，并计算精确度@2。

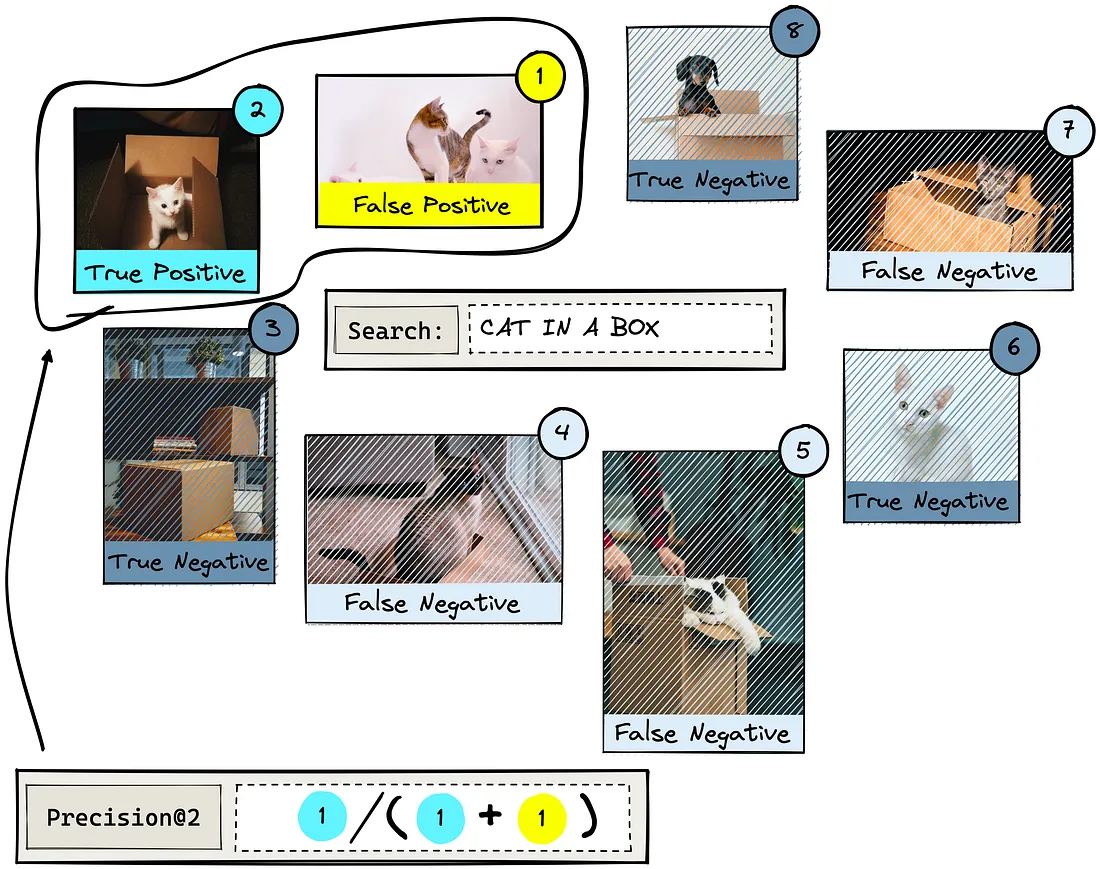
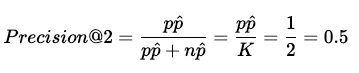
请注意，精度@K 的分母始终等于  K。现在我们有了 precision@K 值，接下来就可以计算平均精度@K (AP@K)：

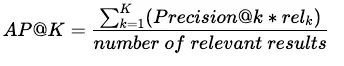
请注意，对于 AP@K，我们取的是所有 k=[1,..., K] 值的平均精度@k 分数。也就是说，对于 AP@5，我们计算的是 k=[1,2,3,4,5]时的精度@k。

我们以前从未见过 rel-k 参数。它是一个相关性参数，（对于 AP@K）当第 k 个项目相关时等于 1，不相关时等于 0。

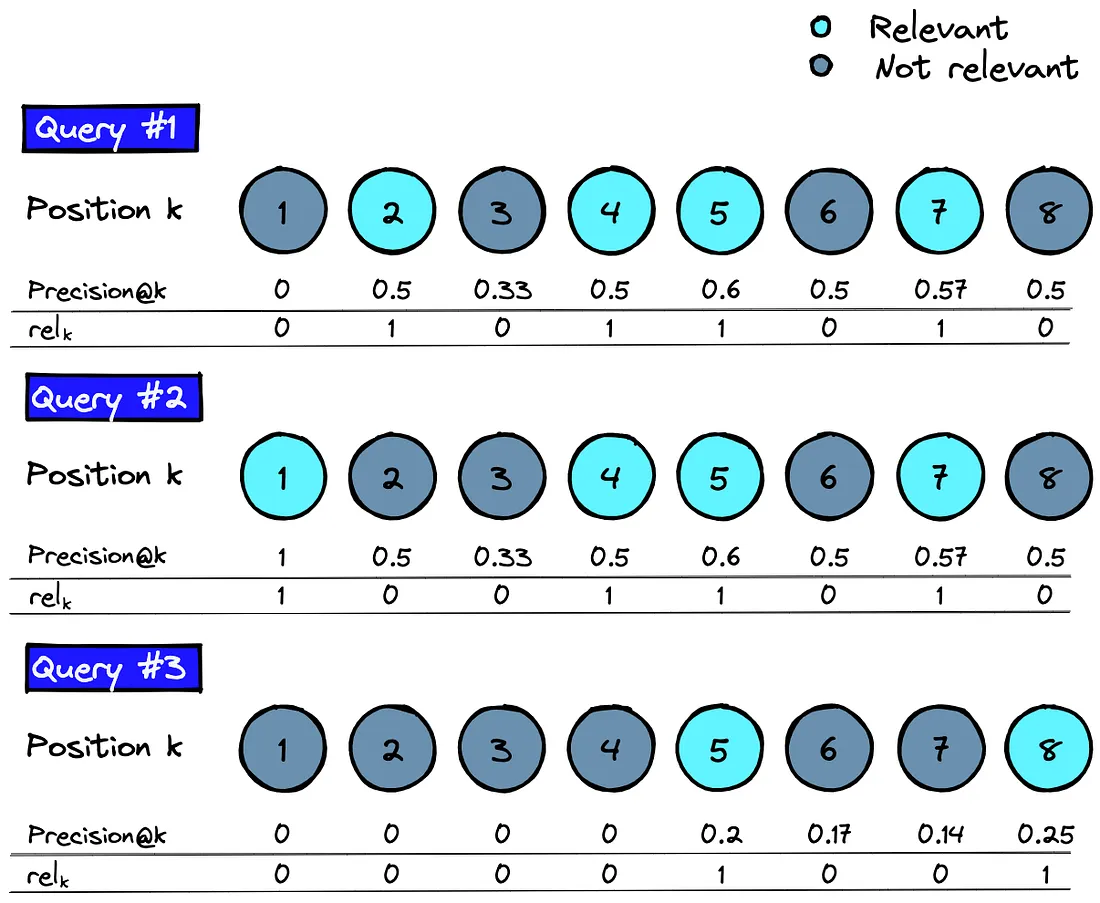
我们使用 k=[1,...,K]迭代计算 precision@k 和 rel-k。

由于我们将 precision@k 和 rel-k 相乘，因此只需考虑与第 k 个项目相关的 precision@k。

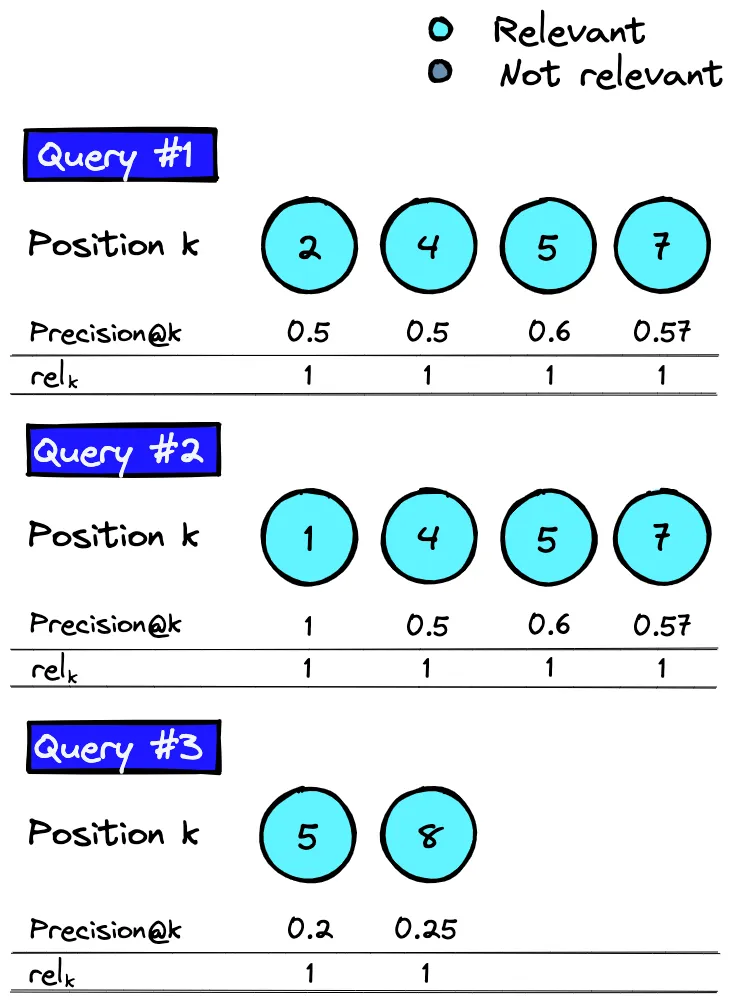
给定这些值后，对于每个查询 q，我们可以计算出 AP@Kq 分数（K=8），计算公式为 ：

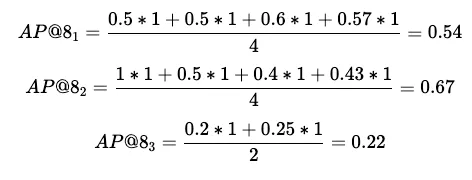
要获得所有查询的平均精度@K (MAP@K) 分数，只需除以查询次数 Q：

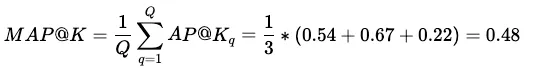
最后，我们得到的 MAP@K 分数为 0.48。要使用 Python 计算所有这些，我们可以这样写：

# initialize variables
actual = [
    [2, 4, 5, 7],
    [1, 4, 5, 7],
    [5, 8]
]
Q = len(actual)
predicted = [1, 2, 3, 4, 5, 6, 7, 8]
k = 8
ap = []
# loop through and calculate AP for each query q
for q in range(Q):
    ap_num = 0
    # loop through k values
    for x in range(k):
        # calculate precision@k
        act_set = set(actual[q])                                                                                                                                   
        pred_set = set(predicted[:x+1])
        precision_at_k = len(act_set & pred_set) / (x+1)
        # calculate rel_k values
        if predicted[x] in actual[q]:
            rel_k = 1
        else:
            rel_k = 0
        # calculate numerator value for ap
        ap_num += precision_at_k * rel_k
    # now we calculate the AP value as the average of AP
    # numerator values
    ap_q = ap_num / len(actual[q])
    print(f"AP@{k}_{q+1} = {round(ap_q,2)}")
    ap.append(ap_q)
# now we take the mean of all ap values to get mAP
map_at_k = sum(ap) / Q
# generate results
print(f"mAP@{k} = {round(map_at_k, 2)}")

输出：

AP@8_1 = 0.54
AP@8_2 = 0.67
AP@8_3 = 0.23
mAP@8 = 0.48

返回相同的 MAP@K 分数 0.480.48。

优点与缺点

MAP@K 是一个简单的离线指标，允许我们考虑返回项目的顺序。这使得它非常适合我们期望返回多个相关项目的使用案例。

MAP@K 的主要缺点是 rel-K 相关性参数是二进制的。我们必须将项目视为相关或不相关。它不允许项目比其他项目的相关性稍高或稍低。

归一化折现累计收益 (NDCG@K)

归一化折现累计收益 @K (NDCG@K) 是另一个顺序感知指标，我们可以从一些更简单的指标中推导出它。从累积收益 (CG@K) 开始，计算方法如下：

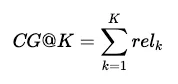
这次的 rel-K 变量有所不同。它是一个相关性等级范围，其中 *0* 是最不相关的，而某个较高的值则是最相关的。等级的数量并不重要；在我们的例子中，我们使用的范围是 0→40→4。

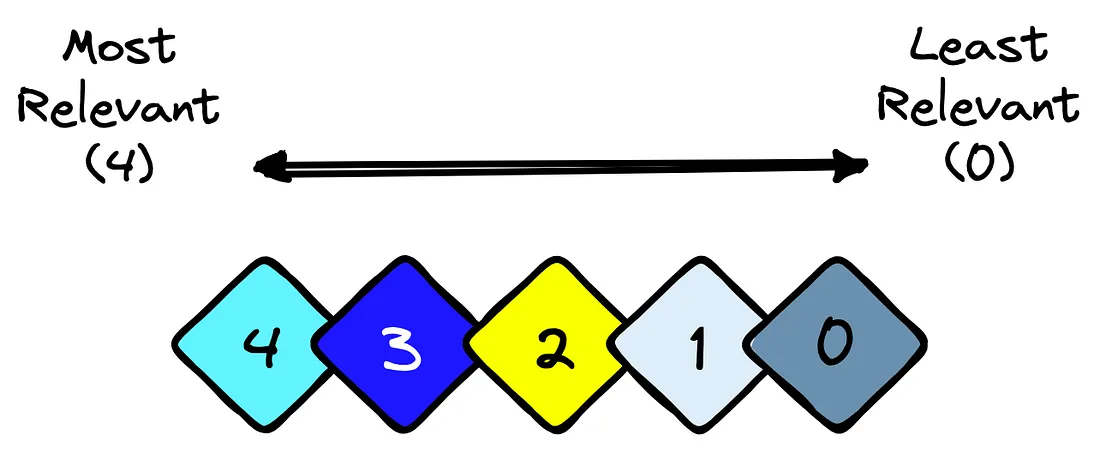
让我们把它应用到另一个例子中。我们将使用与之前类似的八张图片数据集。圈内数字代表IR系统的预测排名，菱形代表     relk 的实际排名。

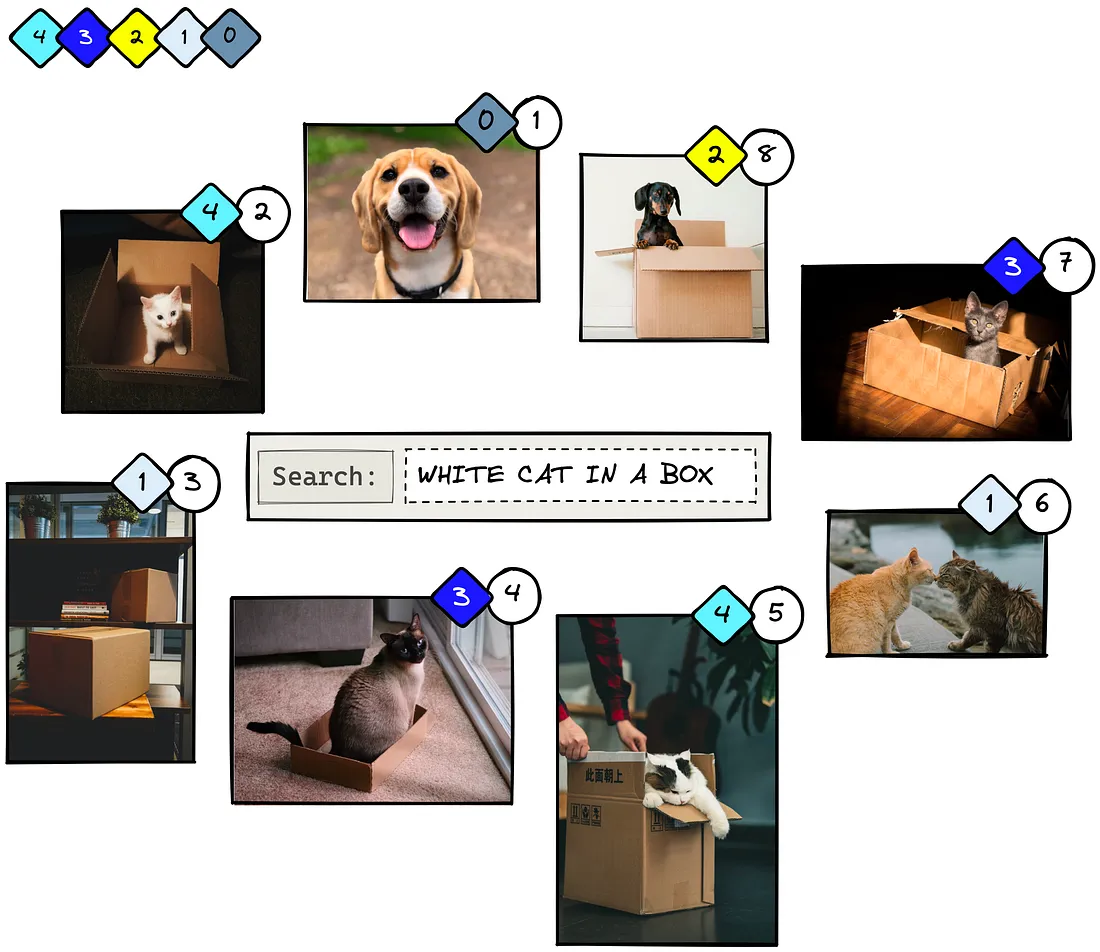
为了计算位置 K 的累积增益 (CG@K)，我们将相关性得分相加，直至预测排名 K。当k=2时：

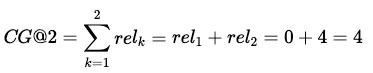
值得注意的是，CG@K 并不区分顺序。如果我们将图片 1 和 2 互换，尽管相关性更高的项目被放在前面，但当 K≥2 时，我们仍会得到相同的分数。

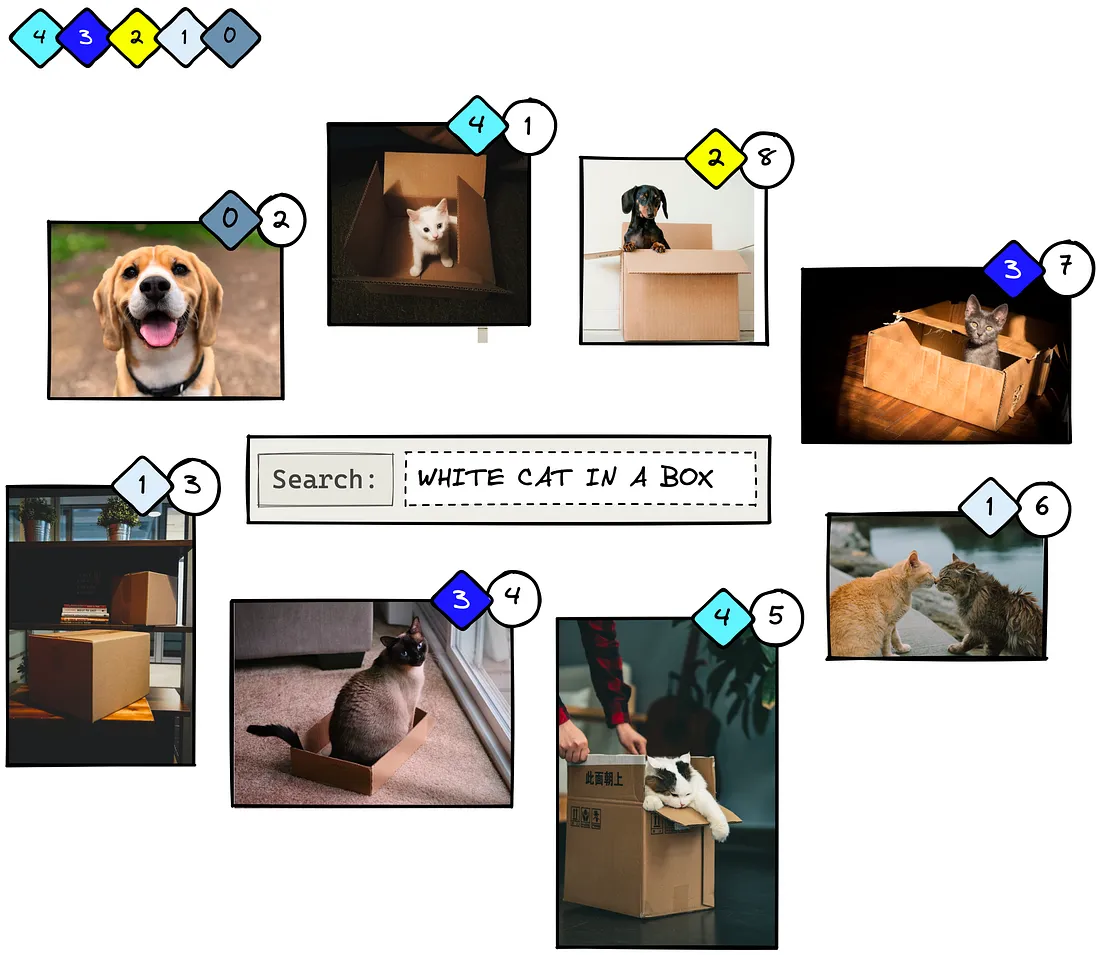
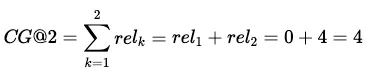
为了处理这种缺乏阶次意识的问题，我们修改了创建 DCG@K 的度量方法，在公式中增加了 log2（1+k）形式的惩罚：

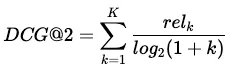
现在，当我们计算 DCG@2 并交换前两张图片的位置时，会得到不同的分数：

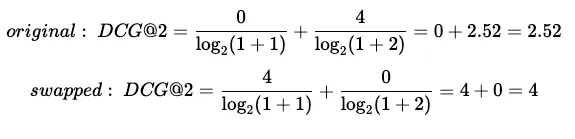
from math import log2
# initialize variables
relevance = [0, 7, 2, 4, 6, 1, 4, 3]
K = 8
dcg = 0
# loop through each item and calculate DCG
for k in range(1, K+1):
    rel_k = relevance[k-1]
    # calculate DCG
    dcg += rel_k / log2(1 + k)

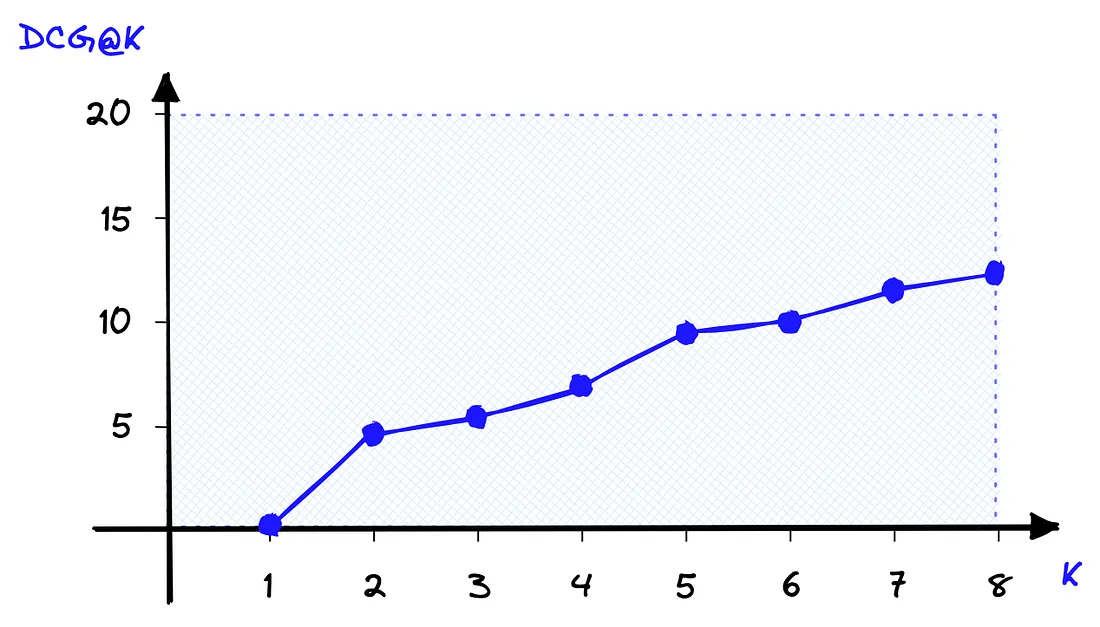
使用顺序感知的 DCG@K 指标意味着首选的交换结果能返回更好的分数。

遗憾的是，DCG@K 分数很难解释，因为其范围取决于我们为数据选择的变量 rel-k 范围。我们使用归一化 DCG@K (NDCG@K) 指标来解决这个问题。

NDCG@K 是对标准 NDCG 的一种特殊修改，它切断了任何排名大于 K 的结果。

NDCG@K 使用理想 DCG@K (IDCG@K) 排名对 DCG@K 进行规范化。对于 IDCG@K，我们假定最相关的条目按相关性顺序排列在最前面。

计算 IDCG@K 只需重新排序分配的等级，并执行相同的 DCG@K 计算即可：

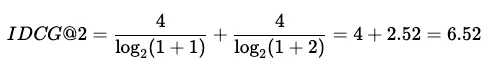
# sort items in 'relevance' from most relevant to less relevant
ideal_relevance = sorted(relevance, reverse=True)
print(ideal_relevance)
idcg = 0
# as before, loop through each item and calculate *Ideal* DCG
for k in range(1, K+1):
    rel_k = ideal_relevance[k-1]
    # calculate DCG
    idcg += rel_k / log2(1 + k)

现在，我们只需使用 IDCG@K 分数对 DCG@K 分数进行归一化处理，即可计算出 NDCG@K：

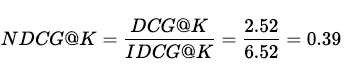
dcg = 0
idcg = 0
for k in range(1, K+1):
    # calculate rel_k values
    rel_k = relevance[k-1]
    ideal_rel_k = ideal_relevance[k-1]
    # calculate dcg and idcg
    dcg += rel_k / log2(1 + k)
    idcg += ideal_rel_k / log2(1 + k)
    # calcualte ndcg
    ndcg = dcg / idcg

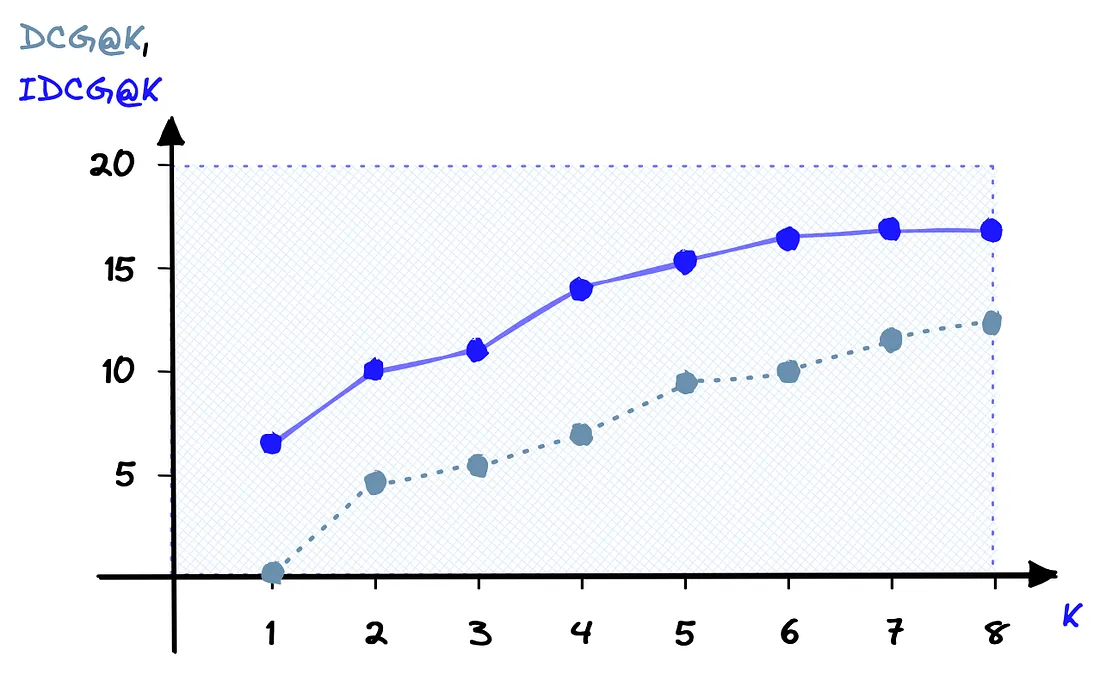
使用 NDCG@K，我们得到的结果是 0.41，这更容易解释，因为我们知道 1.0 是所有项目都完美排序（如 IDCG@K）后得到的最佳分数。

优点和缺点

NDCG@K 是评估IR系统（尤其是网络搜索引擎）最常用的离线指标之一。这是因为 NDCG@K 优化了高度相关的文档，具有顺序感知能力，而且易于解释。

不过，NDCG@K 也有一个明显的缺点。我们不仅需要知道哪些条目与特定查询相关，还需要知道每个条目是否比其他条目更相关/不相关；数据要求更加复杂。

这些是评估信息检索系统最常用的离线指标。单一指标可以很好地反映系统性能。为了对检索性能更有信心，我们可以使用多个指标，就像 Spotify 使用Recall@1、Recall@30 和 MRR@30 一样。

在 A/B 测试过程中，这些指标仍然需要在线指标的最佳支持，这是将我们的检索系统部署到全球之前的下一步。不过，这些离线指标是任何检索项目的基础。

无论我们是在制作第一个产品的原型，还是在评估谷歌搜索的最新迭代，使用这些指标来评估我们的检索系统都将有助于我们部署最佳的检索系统。

总结

在本文中，我们探讨了 "检索增强生成"（RAG）应用中的搜索过程，强调了使用矢量数据库进行语义搜索。它强调了减少处理时间和实时更新等优势。挑战包括对独特查询的响应不佳。预防问题的策略包括监控查询密度和用户反馈。优化工作应侧重于构建和后期制作阶段，包括扩展知识库。该文还讨论了搜索类型、语义搜索以及检索和重新排序管道。建议使用预先训练的模型和离线评估指标，如 Recall@K。总之，本文强调了在 RAG 应用中进行持续优化和全面评估的必要性。