简介

根据过去的数据准确预测未来事件既是挑战也是必要的。从预测股市趋势到预测天气变化，识别随时间变化的模式是预测分析的基石。在为此目的开发的一系列技术中，长短期记忆 (LSTM) 网络成为一种特别强大的工具，可以提供对时间数据序列的细致入微的见解。本文深入探讨了 LSTM 网络在识别随时间变化的模式方面的机制、应用和重要性，强调了它们在各个领域的变革性影响。

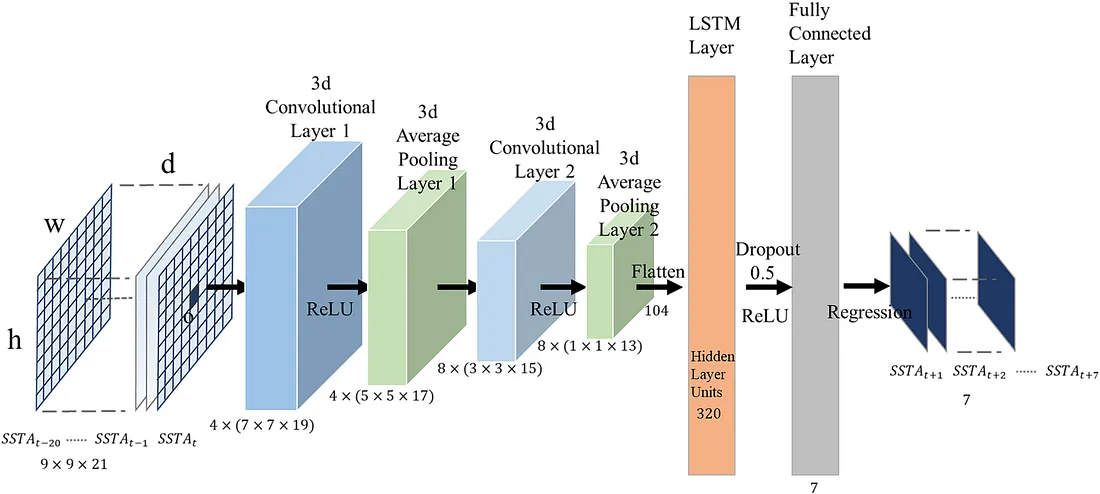
LSTM 网络的机制

LSTM 网络的核心在于其架构，其精心设计旨在解决传统递归神经网络 (RNN) 在处理长数据序列时的局限性。RNN 虽然善于捕捉时间依赖关系，但由于梯度消失问题（即从早期数据点学习的能力会随着序列的延长而减弱），在处理长期依赖关系时往往会出现问题。LSTM 网络通过其独特的组成部分：单元状态和三个调节门（输入门、遗忘门和输出门）来规避这一问题。

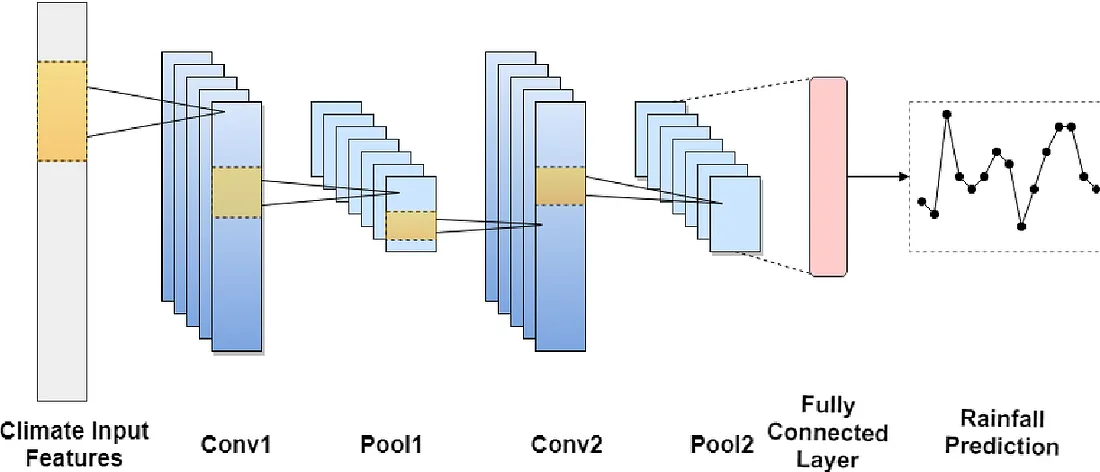
单元状态就像一条传送带，贯穿整个 LSTM 单元链。它可以在多个时间步长内传递相关信息，使网络更容易长期记忆或遗忘信息。栅极由半规管神经网络层组成，用于调节信息在单元状态下的流入和流出。输入门控制向细胞状态添加新信息，遗忘门决定丢弃哪些信息，而输出门则决定当前细胞状态的哪一部分能够进入最终输出。这种复杂的门控机制允许 LSTM 选择性地决定存储、更新或删除哪些信息，从而有效地管理内存并克服长期依赖性带来的挑战。

LSTM 网络的应用

LSTM 网络的多功能性使其被广泛应用于许多对时间模式识别至关重要的领域。在金融市场，它们通过分析历史价格序列和识别潜在趋势来预测股票价格。在自然语言处理（NLP）领域，LSTM 擅长语言建模和机器翻译等任务，在这些任务中，理解前面词语的上下文是生成连贯文本的关键。同样，LSTM 通过学习大量历史天气模式数据集，有助于气象学中更准确的天气预报。此外，LSTM 在连续图像识别中的应用证明了其处理时间和空间依赖关系的能力，从而扩大了其用途。

意义与挑战

LSTM 网络在识别时间模式方面的意义怎么强调都不为过。通过提供一种可靠的机制来处理和学习长数据序列，LSTM 网络能够开发出复杂的预测模型，从而能够非常准确地预测未来事件。这种能力推动了科技进步，并对商业、医疗保健、环境保护等领域的决策过程产生了深远影响。

然而，LSTM 网络的部署并非没有挑战。LSTM 网络结构复杂，需要大量的计算资源和专业知识，这对能力有限的企业造成了限制。此外，预测的质量在很大程度上取决于训练数据的数量和质量，因此需要细致的数据准备和验证，以确保模型的准确性。

代码

我们将通过一个完整的 Python 示例来演示如何使用长短期记忆 (LSTM) 网络来识别随时间变化的模式，尤其是在降水数据的背景下。这包括生成一个模拟降水量随时间变化的合成数据集，建立一个 LSTM 模型来学习这些模式，然后使用适当的指标和图表来评估模型的性能。最后，我们将讨论结果及其影响。

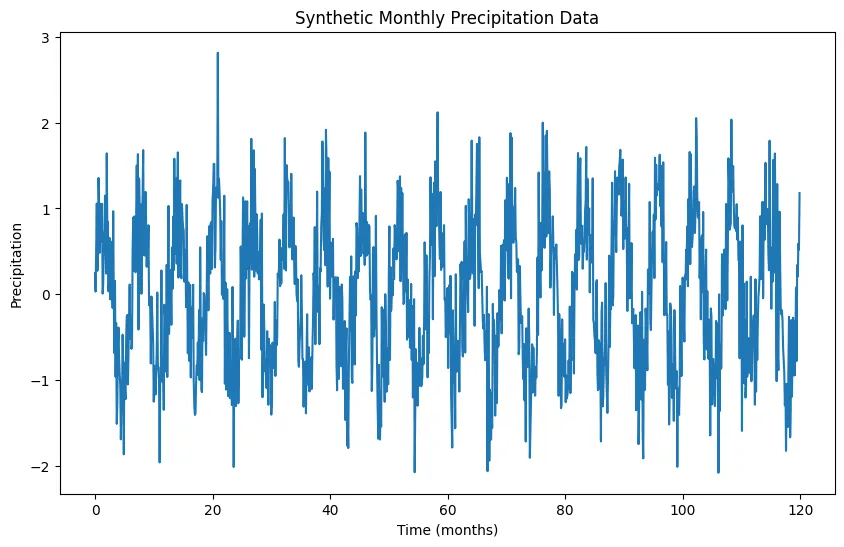
步骤 1：生成合成降水数据

为简单起见，我们的合成数据集将模拟数年的月降水量。我们将使用正弦波生成周期性模式，代表降水的季节性变化，并添加一些噪声来模拟现实世界中的不可预测性。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# Generate synthetic precipitation data
np.random.seed(42)
time = np.arange(0, 120, 0.1)  # 120 months with a step of 0.1 for smooth sine wave
precipitation = np.sin(time) + np.random.normal(scale=0.5, size=len(time))
# Plotting the synthetic data
plt.figure(figsize=(10, 6))
plt.plot(time, precipitation)
plt.title('Synthetic Monthly Precipitation Data')
plt.xlabel('Time (months)')
plt.ylabel('Precipitation')
plt.show()

步骤 2：为 LSTM 准备数据集

LSTM 网络需要特定格式的输入数据，通常是三维形状阵列（样本、时间步长、特征）。我们将对数据进行相应的转换，并将其分成训练集和测试集。

from sklearn.preprocessing import MinMaxScaler
from sklearn.model_selection import train_test_split
# Reshape data and scale
data = precipitation.reshape(-1, 1)
scaler = MinMaxScaler(feature_range=(0, 1))
data_normalized = scaler.fit_transform(data)
# Convert to supervised learning problem
def create_dataset(dataset, look_back=1):
    X, Y = [], []
    for i in range(len(dataset)-look_back-1):
        a = dataset[i:(i+look_back), 0]
        X.append(a)
        Y.append(dataset[i + look_back, 0])
    return np.array(X), np.array(Y)
look_back = 10
X, Y = create_dataset(data_normalized, look_back)
X = np.reshape(X, (X.shape[0], X.shape[1], 1))
# Splitting dataset into train and test sets
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)

步骤 3：构建和训练 LSTM 模型

现在，我们将使用 Keras 定义和训练 LSTM 模型。

from keras.models import Sequential
from keras.layers import LSTM, Dense
# Build LSTM model
model = Sequential()
model.add(LSTM(50, input_shape=(look_back, 1)))
model.add(Dense(1))
model.compile(optimizer='adam', loss='mean_squared_error')
# Train the model
model.fit(X_train, Y_train, epochs=100, batch_size=32, verbose=2)

步骤 4：评估模型

训练结束后，我们将评估模型在测试数据集上的性能，并绘制预测值与实际值的对比图。

# Making predictions
train_predict = model.predict(X_train)
test_predict = model.predict(X_test)
# Invert predictions
train_predict = scaler.inverse_transform(train_predict)
Y_train_inv = scaler.inverse_transform([Y_train])
test_predict = scaler.inverse_transform(test_predict)
Y_test_inv = scaler.inverse_transform([Y_test])
# Calculate RMSE
from sklearn.metrics import mean_squared_error
trainScore = np.sqrt(mean_squared_error(Y_train_inv[0], train_predict[:,0]))
print(f'Train Score: {trainScore:.2f} RMSE')
testScore = np.sqrt(mean_squared_error(Y_test_inv[0], test_predict[:,0]))
print(f'Test Score: {testScore:.2f} RMSE')
# Plotting
plt.figure(figsize=(10, 6))
plt.plot(Y_test_inv[0], label='True Value')
plt.plot(test_predict[:,0], label='Predicted')
plt.title('Precipitation Prediction')
plt.xlabel('Time')
plt.ylabel('Precipitation')
plt.legend()
plt.show()

结果和解释

均方根误差（RMSE）衡量模型预测响应的准确程度，它是预测值与实际观测值之间平方差均值的平方根。一般来说，RMSE 越小越好。

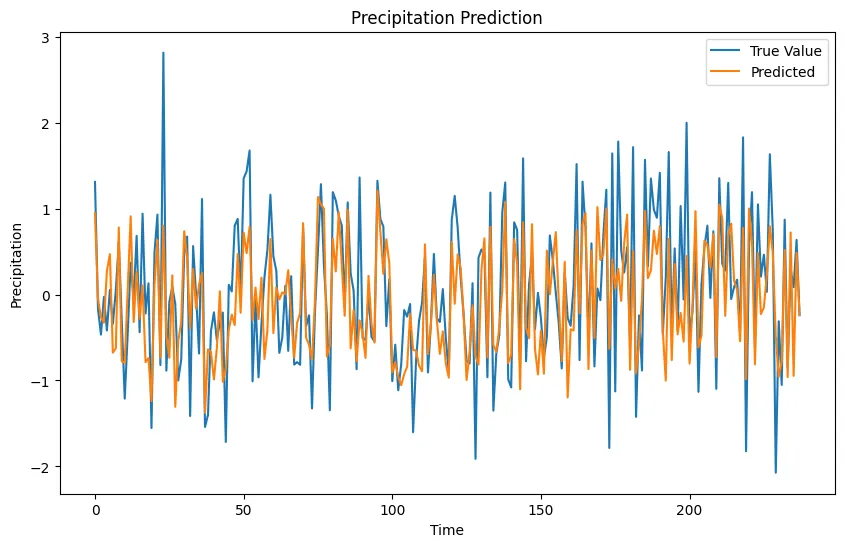
通过实际值与预测值的对比图，我们可以直观地了解模型在哪些方面表现良好，哪些方面表现不佳。鉴于数据的合成性质和 LSTM 模型的简单性，结果可能会有所不同。在实际应用中，可能需要进一步调整模型参数（如回看、多个 LSTM 单元、历时等）和更复杂的模型架构，以提高准确性。

总之，LSTM 网络为识别随时间变化的模式提供了一个强大的工具，特别是在天气预报等应用中，时间依赖性起着至关重要的作用。建模和预测降水模式的能力展示了 LSTM 在分析连续数据方面的众多潜在用途之一。

该图显示了预测模型在训练和测试数据集上的性能结果，降水的真实值与模型生成的预测值并列。

Train Score: 0.56 RMSE
Test Score: 0.60 RMSE

训练集和测试集的 RMSE（均方根误差）得分比较接近，训练得分为 0.56，测试得分为 0.60。这些数值表明，鉴于测试得分略高于训练得分，模型对未见数据的泛化效果相对较好。

解释图和 RMSE 分数：

1. 预测接近度： 预测值与真实值的接近程度表明，模型以合理的准确度捕捉到了数据中的基本模式。
2. 通用性： 由于测试 RMSE 没有明显高于训练 RMSE，我们可以推断模型没有过度拟合训练数据。如果训练 RMSE 较低，而测试 RMSE 高得多，则表明模型存在过度拟合。
3. 数据波动： 模型似乎能很好地跟踪真实数据的波动，但在某些点上，预测值与真实值存在偏差。这在意料之中，因为合成数据可能包含随机噪声，而随机噪声是无法完全预测的。
4. 模型性能： 均方根误差（RMSE）值表明，在训练期间，模型预测值与实际值的误差平均在 0.56 个单位以内，在测试期间则在 0.60 个单位以内。由于不知道什么是降水测量中的重大误差，我们无法断定这是否是一个好的模型。不过，均方根误差值表明模型的准确性处于中等水平。
5. 改进： 如果需要更准确的预测，可以进一步调整模型参数，增加模型的复杂性，或者对输入数据进行不同的预处理。

总之，该模型在预测一段时间内的降水模式方面似乎做得不错。值得注意的是，在实际应用中，尤其是在环境科学领域，即使是 RMSE 的微小改进也会对预测质量及其在决策过程中的实用性产生重大影响。

结论

长短期记忆网络在理解和预测时间模式方面起着关键作用。通过克服以往模型的局限性，它们为分析各个领域的时间数据提供了新的可能性。随着技术的发展和计算能力的提高，LSTM 网络的潜在应用领域必将不断扩大，进一步巩固其在机器学习领域的基础工具地位。尽管 LSTM 模型在实施过程中面临诸多挑战，但其不断完善的过程有望提高其易用性和效率，为未来更具创新性和影响力的应用铺平道路。