追求专业化

在挑战难题时，分而治之往往是一种有价值的解决方案。无论是亨利-福特的装配线、合并排序分割数组的方式，还是整个社会倾向于让人们专门从事特定的工作，这样的例子不胜枚举！

自然而然，当人们开始着手教授计算机推理时，将机器的任务分成若干部分是很有意义的，例如，数学部分、科学部分、语言部分等等。

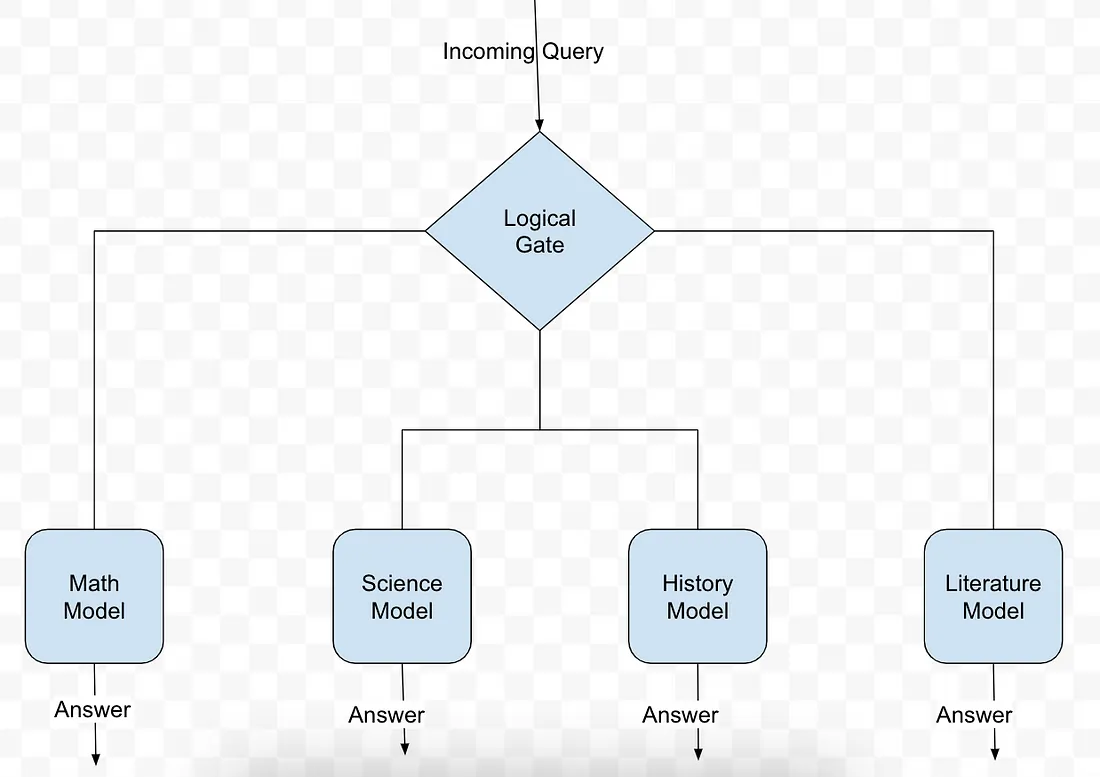
然而，这一想法尚未成功实现。失败的原因可能与我们的大脑没有近乎独立的组成部分一样：复杂的推理需要协同使用许多不同的部分，而不是单独使用。

长久以来，这一想法一直处于休眠状态，直到人们不再试图在数学或科学的高层次上创建不同的组件，而是在这些神经网络的最底层--代币--创建不同的组件。

论文《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》详细介绍了如何在令牌层创建专家，这在降低成本和提高响应质量方面都非常有效。

代币级专家混合物

我们先来了解一下 "专家 "的概念。专家是前馈神经网络。我们通过门将信号传递给特定专家，然后将它们连接到我们的主模型。你可以想象，我们的神经网络将这些专家视为一层中更复杂的神经元。

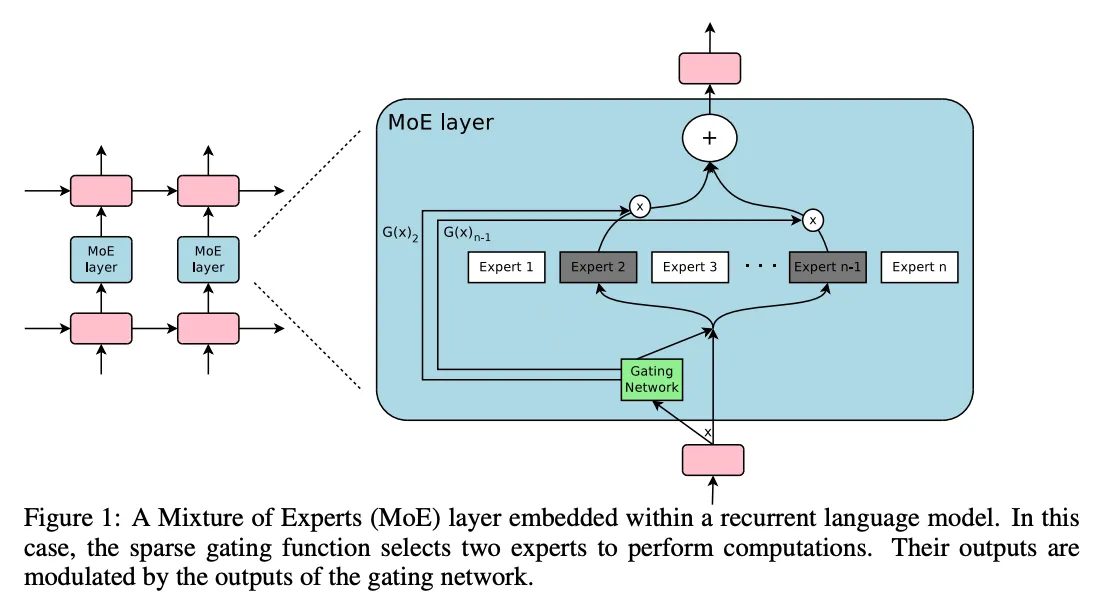
简单地实现门的问题在于，你显着增加了神经网络的计算复杂性，可能会使你的培训成本巨大（尤其是对于法学硕士）。那么如何解决这个问题呢？

条件计算与稀疏门控专家混合物

这里的问题在于，只要有任何信号传到神经元，神经网络就必须计算该神经元的值，因此即使是发送到专家的最微弱的信息量也会触发整个专家网络进行计算。论文作者通过创建一个函数 G(x)来解决这一问题，该函数可强制将大多数低值信号计算为零。

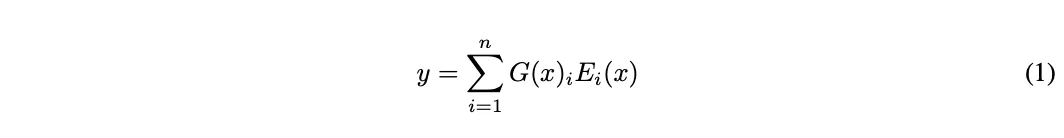
在上式中，G(X) 是我们的门控函数，E(x) 是代表我们的专家的函数。由于任何数字乘以零都是零，因此当我们的门控函数给出一个零时，这一逻辑可以避免我们运行专家网络。那么，门控函数是如何决定计算哪些专家的呢？

门控函数

门控函数本身是一种相当巧妙的方法，可以只关注你想要的专家。让我们先看看下面的等式，然后我会深入分析它们是如何工作的。

从下往上看，等式 5 只是一个阶跃函数。如果输入值不在某个范围内（这里是列表 v 的前 k 个元素），它将返回-无穷大，从而确保在输入 Softmax 时是一个完美的 0。如果数值不是-无穷大，则会有信号通过。通过 k 参数，我们可以决定要听取多少位专家的意见（k=1 将只路由到 1 位专家，k=2 将只路由到 2 位专家，等等）。

等式 4 是我们如何确定从列表中选择前 k 值的方法。首先，我们将门的输入（信号 x）乘以某个权重 Wg。这个 Wg 就是神经网络在每一轮连续训练中要训练的权重。请注意，与每个专家相关的权重可能都有一个不同的值。现在，为了防止每次都选择同一个专家，我们可以通过等式的后半部分加入一些统计噪声。作者建议沿着正态分布分布这种噪声，但关键的想法是加入一些随机性来帮助专家选择。

等式 3 简单地将这两个等式结合起来，并将它们放入一个 SoftMax 函数中，这样我们就能确保-无穷大为 0，而任何其他值都会向专家发送信号。

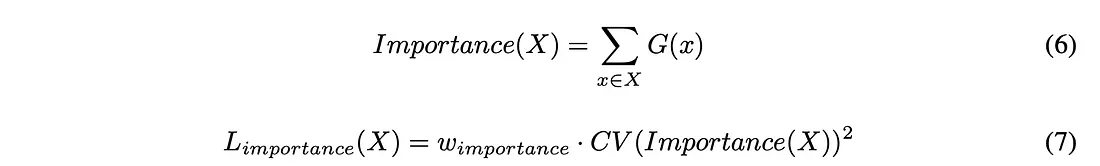
标题中的 "稀疏 "一词来源于稀疏矩阵，即大部分数值为零的矩阵，这正是我们使用门控函数有效创建的矩阵。

优化损失函数，平衡专家使用率

虽然我们的噪声注入对降低专家集中度很有价值，但作者发现这还不足以完全解决这个问题。为了激励模型平均使用专家，他们调整了损失函数。

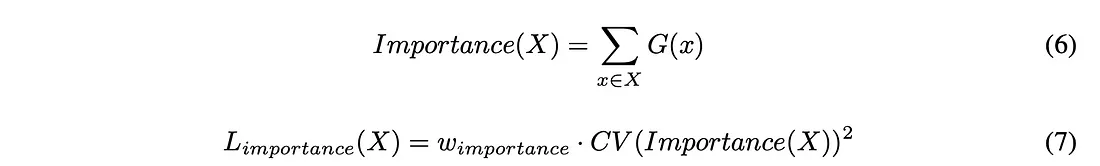
等式 6 显示了他们是如何根据门函数来定义重要性的--这是有道理的，因为门函数最终决定了哪位专家会被使用。这里的重要性是所有专家门函数的总和。他们将损失函数定义为重要性集合的变化系数。简单地说，这意味着我们要找到一个能代表每位专家被使用程度的值，少数专家被使用会产生一个大值，而所有专家都被使用则会产生一个小值。w 重要性是一个超参数，可以帮助模型使用更多的专家。

为专家提供足够的训练数据

论文中提到的另一个训练难题是如何为每位专家提供足够的数据。由于我们的门控功能，每位专家看到的数据量只是相对密集的神经网络看到的数据量的一小部分。换句话说，由于每位专家只能看到训练数据的一部分，因此我们实际上就像是把训练数据的大部分隐藏起来，不让这些专家看到。这使得我们更容易出现拟合过度或拟合不足的情况。

Mixtral 的实现和 Grok

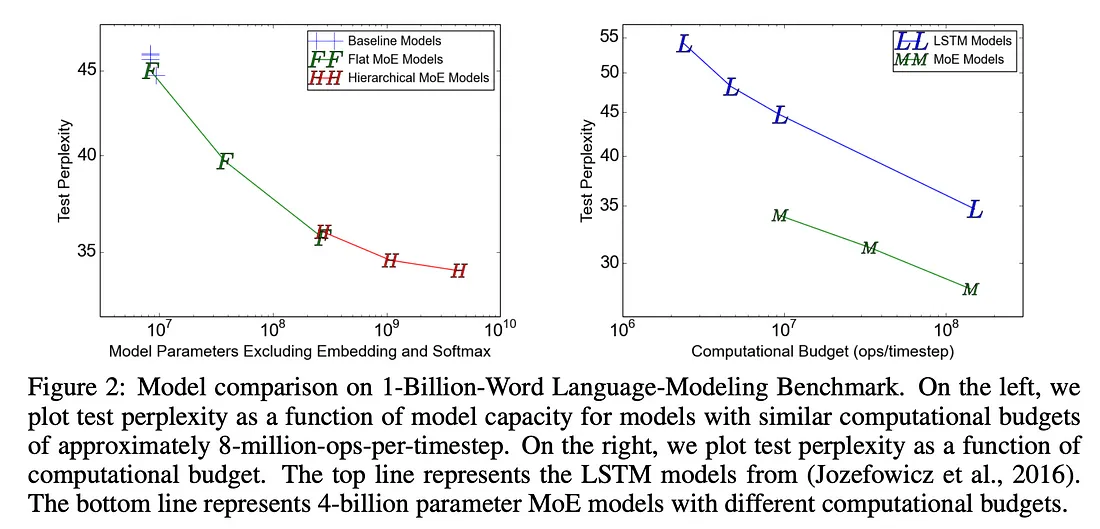
《Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer》论文发表于 2017 年，同年，开创性的《Attention is All You Need》论文也发表了。正如《Self-Attention》中描述的架构花了几年时间才成为主流一样，我们也花了几年时间才拥有任何可以成功实现这种稀疏架构的模型。

当 Mistral 于 2024 年发布 Mixtral 模型时，他们向世界展示了这种架构的强大功能。有了第一个采用这种架构的量产级 LLM，我们就可以看看它是如何利用其专家进行进一步研究的。这里最吸引人的一点是，我们并不真正了解为什么令牌级的专业化如此有效。如果你看看下图中的 Mixtral，就会发现除了数学之外，没有哪位专家是任何一门高水平学科的首选。

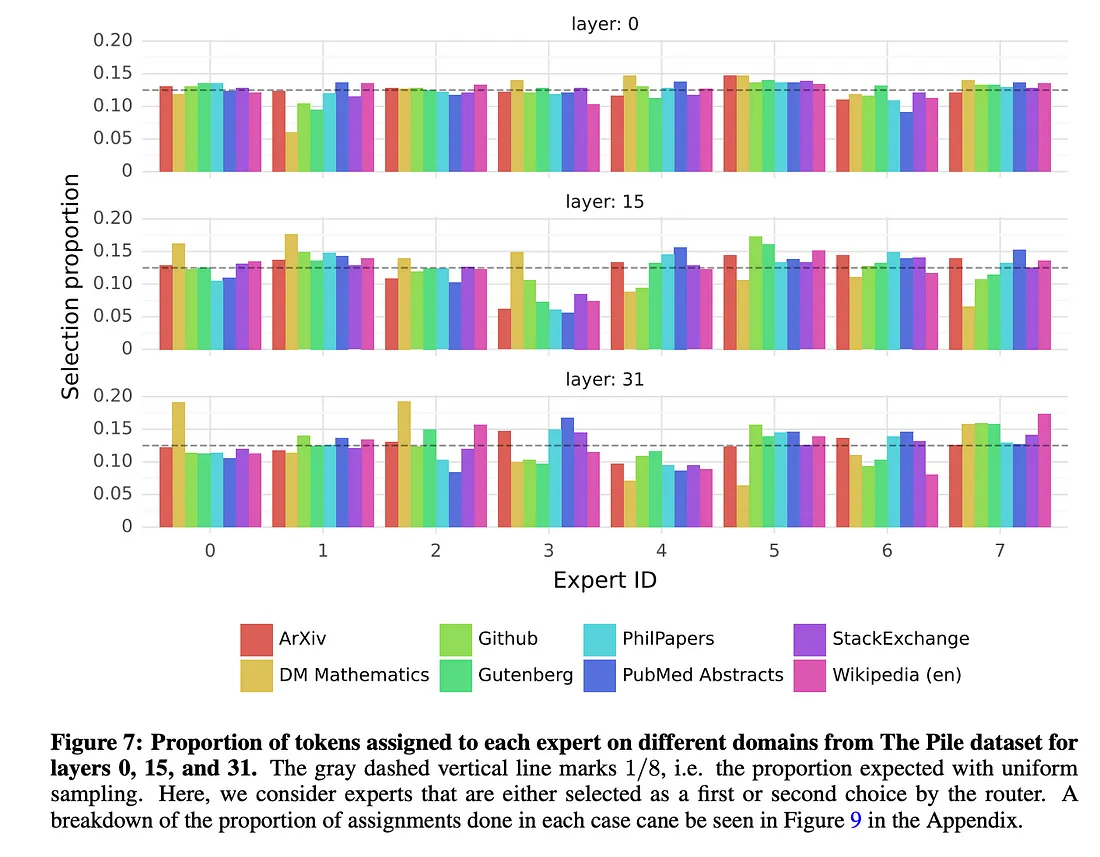
因此，我们遇到了一个耐人寻味的情况：这一新的架构层有了明显的改进，但却没有人能解释清楚为什么会这样。

更多的主要参与者也在关注这一架构。随着 Grok-1 的公开发布，我们现在知道 Grok 是一个稀疏专家混合模型，拥有 3140 亿个参数。显然，这是一种人们愿意投入大量资金的架构，因此很可能成为下一波基础模型的一部分。该领域的主要参与者正在迅速行动，将这一架构推向新的极限。

结论

“Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer”一文最后指出，通过递归神经网络创建的专家自然是下一步的目标，因为递归神经网络往往比前馈神经网络更加强大。如果真是这样，那么基础模型的下一个前沿可能不是参数更多的网络，而是拥有更复杂专家的模型。