主成分分析 (PCA) 已用于交通数据中以检测异常情况，但它也可用于捕获公交站交通历史记录的模式，就像它对客户的购买数据所做的那样。

1. PCA 有哪些技巧

简而言之，PCA 通过寻找特征的线性组合来归纳数据，这就好比给一个 3D 物体拍几张照片，它会很自然地将照片从最具代表性的到最不具代表性的排序，然后再交给你。

输入是我们的原始数据，PCA 会有两个有用的输出：Z 和 W。将它们相乘，我们就能得到重建数据，即原始数据，但有一些可容忍的信息损失（因为我们已经降低了维度）。

我们将在下面的实践中用数据来解释这两个输出矩阵。

2. 应用 PCA 后我们能做什么

将 PCA 应用于数据降维后，我们可以将其用于其他机器学习任务，例如聚类、分类和回归。

在本文后面的台北捷运案例中，我们将对低维数据进行聚类，其中几个维度可以理解为一天中不同时段的乘客比例，如早上、中午和晚上。白天乘客比例相似的车站将被视为同一聚类（它们的模式相似！）。

3. 看看我们的交通数据集！

我们使用的数据集是台北捷运系统每小时交通数据，列有：日期、小时、起点、终点、乘客数。

在我们的案例中，我只保留平日的数据，因为平日里不同车站之间会有更多有趣的模式，例如位于住宅区的车站可能在白天有更多乘客进入，而在晚上，位于商业区的车站可能有更多乘客进入。

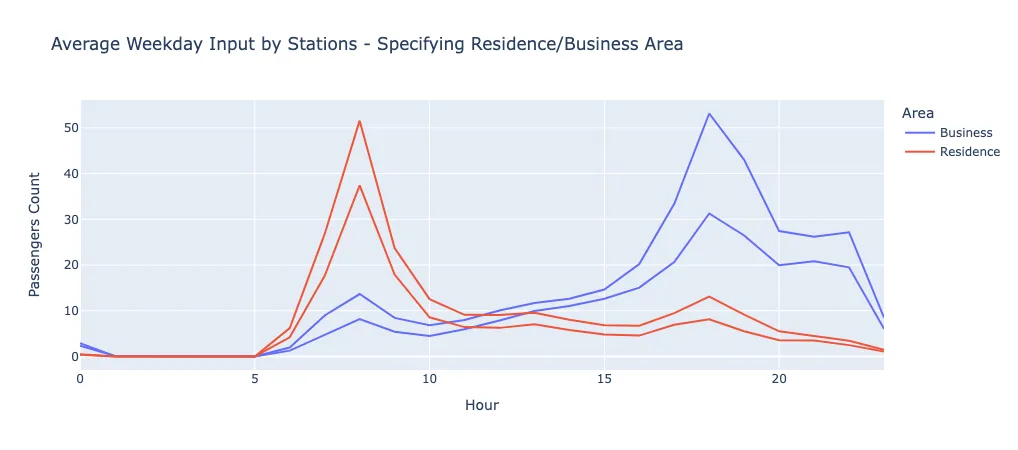
上图是 4 个不同车站的每小时客流量趋势（进站乘客量）。红色的两条线是新埔线和永安市场线，这两条线实际上位于新北市的超级拥挤区域。而蓝色的两条线路则是台北市政府和忠孝复兴，这里是大多数公司和商业活动的聚集地。

这些趋势反映了这些地区和车站的性质，我们可以发现，在上下班时间（上午 7 点至 9 点，下午 17 点至 19 点）比较它们的趋势，差异最为明显。

4. 对每小时交通数据使用 PCA

为什么要在执行进一步的机器学习任务之前降低维度？

主要有两个原因：

1. 随着维数的增加，所有数据点在很多方面都显得稀疏和不相似，这被称为 "维度诅咒"。
2. 由于交通数据的高维特性，很难对其进行可视化和解释。

通过应用 PCA，我们可以找出不同站点交通趋势最明显、最具代表性的时段。直观地说，通过前面的图示，我们可以认为上午 8 点和下午 18 点左右的时间段可能具有代表性，足以对车站进行聚类。

原始数据 X

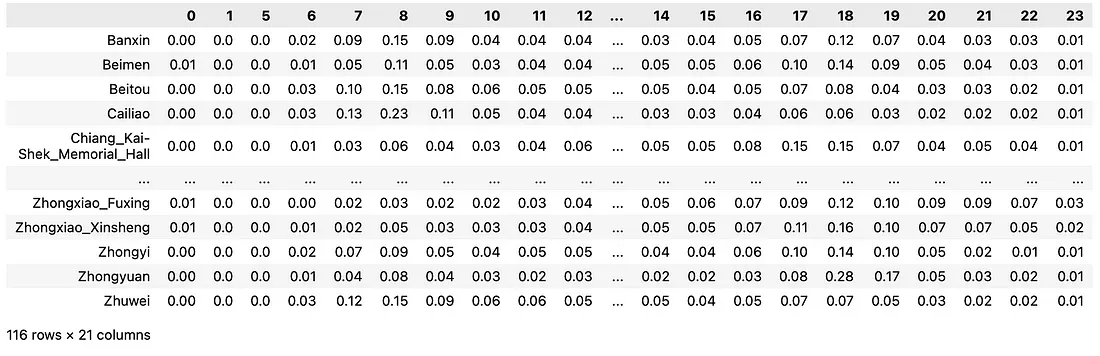
• 索引：车站
• 列：小时
• 值：特定小时内进站乘客的比例（每个车站：#乘客数/#乘客总数）

有了这样的 X，我们就可以通过以下代码应用 PCA：

from sklearn.decomposition import PCA
n_components = 3
pca = PCA(n_components=n_components)
X_tran = StandardScaler().fit_transform(X)
pca = PCA(n_components=n_components, whiten=True, random_state=0)
pca.fit(X_tran)

在这里，我们指定参数 n_components 为 3，这意味着 PCA 将为我们提取 3 个最重要的成分。

请注意，这就好比 "给一个 3D 物体拍几张照片，然后按照代表性最强到最弱的顺序排列"，然后我们选择前 3 张照片。因此，如果我们将 n_components 设为 5，就会多出 2 张图片，但前 3 张仍然不变！

PCA 输出，W 矩阵

W 矩阵可以看作是与我们的 "图片"（或者更具体地说是主成分）相关的每个特征（即小时数）的权重。

pd.set_option('precision', 2)'precision', 2)
W = pca.components_
W_df = pd.DataFrame(W, columns=hour_mapper.keys(), index=[f'PC_{i}' for i in range(1, n_components+1)])
W_df.round(2).style.background_gradient(cmap='Blues')

就我们的 3 个主成分而言，我们可以看到 PC_1 更偏重于夜间时间，PC_2 更偏重于中午时间，而 PC_3 则偏重于上午时间。

PCA 输出，Z 矩阵

我们可以将 Z 矩阵理解为站点的代表。

Z = pca.fit_transform(X)
# Name the PCs according to the insights on W matrix
Z_df = pd.DataFrame(Z, index=origin_mapper.keys(), columns=['Night', 'Noon', 'Morning'])
# Look at the stations we demonstrated earlier
Z_df = Z_df.loc[['Zhongxiao_Fuxing', 'Taipei_City_Hall', 'Xinpu', 'Yongan_Market'], :]
Z_df.style.background_gradient(cmap='Blues', axis=1)

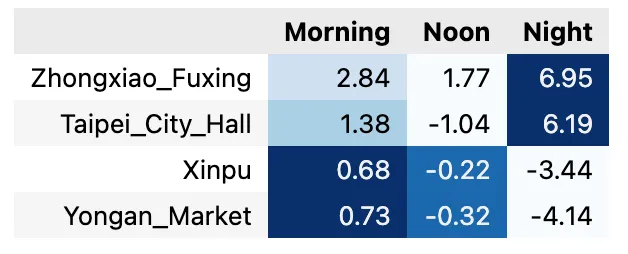
在我们的案例中，由于我们对 W 矩阵进行了解释，并理解了各成分的潜在含义，因此可以为 PC 赋名。

这 4 个站点的 Z 矩阵表明，前两个站点的夜间时间比例较大，而另外两个站点的上午时间较 多。这一分布也与我们的 EDA 发现相吻合。

5. 用 K-Means 对 PCA 结果进行聚类

在得到 PCA 结果后，让我们进一步根据交通模式对中转站进行聚类。

在上面，Z 矩阵代表了夜间、中午和早晨的车站。

我们将根据这些表征对车站进行聚类，从而使同一组中的车站在这三个时间段的乘客分布情况相似。

聚类方法有很多，如 K-Means、DBSCAN、分层聚类等。由于这里的主要议题是了解 PCA 的便利性，我们将跳过试验哪种方法更合适的过程，直接使用 K-Means。

from sklearn.cluster import KMeans
# Fit Z matrix to K-Means model 
kmeans = KMeans(n_clusters=3)
kmeans.fit(Z)

拟合 K-Means 模型后，让我们用 plotly 绘制三维散点图来直观显示聚类。

import plotly.express as px
cluster_df = pd.DataFrame(Z, columns=['PC1', 'PC2', 'PC3']).reset_index()
# Turn the labels from integers to strings, 
# such that it can be treated as discrete numbers in the plot.
cluster_df['label'] = kmeans.labels_
cluster_df['label'] = cluster_df['label'].astype(str)
fig = px.scatter_3d(cluster_df, x='PC1', y='PC2', z='PC3', 
                       color='label', 
                       hover_data={"origin": (pca_df['index'])},
                       labels={
                          "PC1": "Night",
                          "PC2": "Noon",
                          "PC3": "Morning",
                          },
                      opacity=0.7,
                      size_max=1,
                      width = 800, height = 500
                    ).update_layout(margin=dict(l=0, r=0, b=0, t=0)
                    ).update_traces(marker_size = 5)

6. 对台北捷运交通的启示--聚类结果

• 第 0 组 ： 白天乘客较多，因此可能是 "生活区 "组。
• 第 2 组 ： 晚间乘客较多，因此可能是 "商业区 "组。
• 第 1 组：白天和晚上都有很多人进入车站，要解释这些车站的性质比较复杂，因为不同的车站可能有不同的原因。下面，我们将对该组中的两个极端情况进行分析。

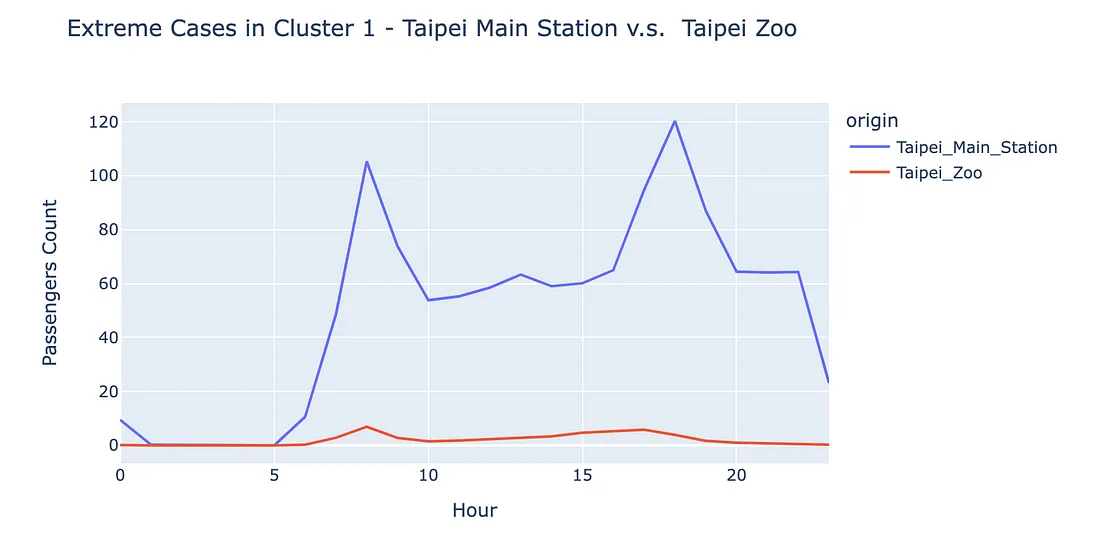
例如，在第一组中，客流量最大的车站台北车站是台北市的一个大型交通枢纽，乘客可以在这里从公共汽车和铁路系统换乘捷运。因此，早晚人流量大的特点十分明显。

相反，台北动物园站虽然也在第一群聚区，但并不是 "白天晚上都人满为患"。相反，这两个时段的人流都不多，因为该区域附近居民很少，大多数市民平日也很少去台北动物园。

这两个站点的模式不太一样，但却在同一个群组中。也就是说，群组 1 中可能包含了太多实际上并不相似的站点。因此，今后我们必须对 K-Means 的超参数（如聚类数）进行微调，剪影得分和肘法等方法也会有所帮助。

结论

综上所述：

1. 将 PCA 应用于交通数据以降低维度，可以实现从 21 个工作小时中提取 3 个重要时段（早、中、晚）。
2. PCA 的输出结果是 W 矩阵和 Z 矩阵，其中 Z 矩阵可以看作是车站在主成分（时间段）方面的表示，而 W 矩阵可以看作是主成分（时间段）在原始特征（小时数）方面的表示。
3. 考虑 W 矩阵有助于我们理解每个主成分的潜在含义。
4. 聚类方法可用于 PCA 输出 Z 矩阵。