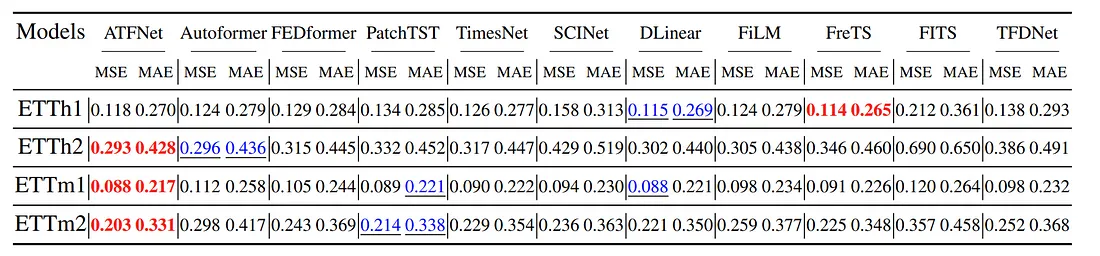
ATFNet:用于长期时间序列预测的自适应时频集成网络
ATFNet 是一种深度学习模型,它结合了时域和频域模块,以捕捉时间序列数据中的依赖关系。它引入了一种新颖的加权机制,可根据周期性调整权重,增强了离散傅里叶变换,还包括一种复值频谱关注机制,用于辨别错综复杂的关系。
时间序列数据的挑战:
时间序列的挑战之一来自两个概念:周期性和非周期性。
周期性是指在任何给定时间内,数值都取决于某个时间之前的某个数据点,更具有全局性;而非周期性是指与附近数据点的依赖关系,更具有局部性。在进行时间序列预测时,将两者都考虑在内是一项挑战。
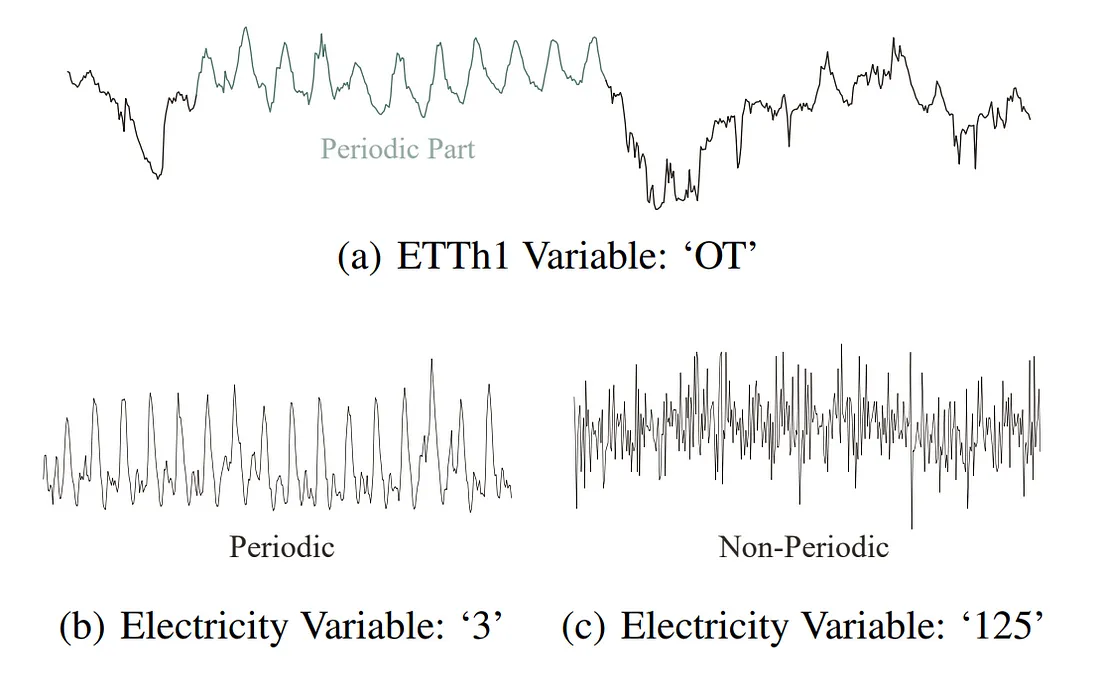
此外,时间序列(TS)分析有两种域,即时域和频域。
时域是指随着时间的推移信号强度的变化,而频域则是从频率的角度分析时间序列。
前者有助于理解局部依赖关系,后者有助于理解全局依赖关系。
将两者混合是一种很好的方法,但需要高效地完成,除非我们不能同时利用两者的优势。
ATFNet 框架(此处提出的模型)旨在应对处理现实世界时间序列数据中不同周期属性混合的挑战。这种结合可以利用时域和频域表示法的优势进行综合分析。

ATFNet 主要由三个子部分组成:
- T-Block 从时域捕捉局部依赖性。
- F-Block 从频域捕捉全局相关性。扩展 DFT 用于生成输入序列的频率对齐频谱。
- 主导谐波序列能量加权法会根据输入序列的周期属性为 F-Block 和 T-Block 分配适当的权重。
扩展 DFT:
在这里,我们使用 ATFNet 中的扩展 DFT 来调整输入序列的频谱,从而对时间序列数据进行更全面的分析。我们只考虑输出的前半部分(删除后半部分),从而降低了成本。
完整序列的 DFT 基础如下:

这样,我们就得到了一个长度为 L + T 的频谱,它与完整序列的 DFT 频谱相一致。
一般架构:
- T 字块
- F 块
- 主谐波序列能量加权
一般来说,输入有两个方向,首先是 T-Block,其次是扩展 DFT,然后是 F-Block。
F-Block
请注意,F-Block 是在最初的注意力(注意力就是你所需要的一切)基础上稍加修改而成的。一言以蔽之,注意力机制是神经网络的下一个层次,它将一切事物路由到一切事物,从而对数据进行学习和泛化。它效率不高,但功能强大,尽管有很多修改可以使它更有效。
然后我们对 F 进行归一化处理,以便用 RevIN 方法处理频域频谱(我们在最后对其进行去归一化处理)。
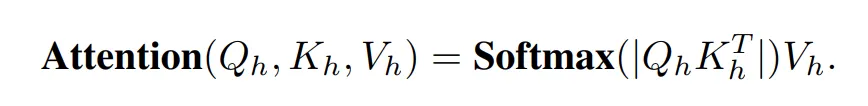
然后,复值频谱注意力的最终输出计算如下:

可逆实例归一化(RevIN)是一种具有可学习仿射变换的归一化和去归一化方法。RevIN 可应用于任何深度神经网络,是一种与模型无关的方法。
请注意,这里禁用了位置嵌入(未使用)。
T 块
这部分负责数据的局部依赖性,换句话说,就是时域。我们将每个小补丁嵌入编码器变换器,最后使用线性投影生成输出。请注意,这里也使用了 RevIN(用于分布偏移)。
主谐波列能量加权
主导谐波序列能量加权机制可根据输入序列的周期特性动态调整时域和频域模块之间的权重。
结果: