在大型语言模型方面，微调可能是讨论最多的技术问题之一。大多数人都知道，训练这些模型的成本很高，而且需要大量的资金投入，因此，通过使用已有的模型并结合自己的数据对其进行微调，就能创建出独一无二的模型，这一点令人兴奋。

对模型进行微调的方法有多种，但目前最流行的方法之一是 "LoRA：大型语言模型的低等级自适应 "论文中讨论的 LoRA 方法（Low Rank Adaptation 的缩写）。

在深入了解 LoRA 背后的机制之前，我们需要了解一些矩阵背景和微调机器学习模型的一些基本知识。

矩阵背景术语

实际上，所有机器学习模型都将权重存储为矩阵。因此，了解一些线性代数知识有助于直观地了解发生了什么。

从一些基础知识开始，我们可以看到矩阵中的行和列

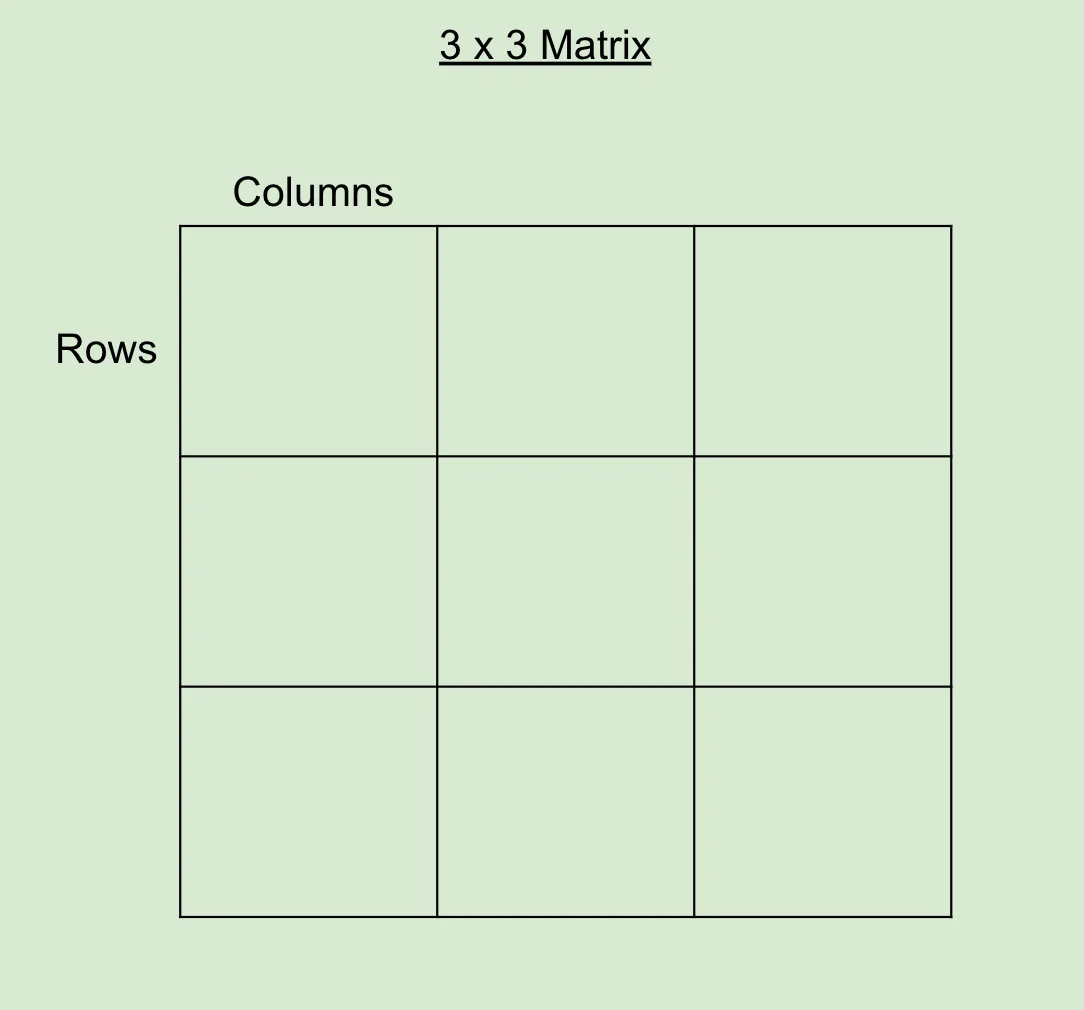
当然，行数、列数或两者都越多，矩阵占用的数据也就越多。有时，行和（或）列之间存在一种数学关系，可以用来减少所需的空间。这就好比一个函数所占用的空间要远远小于它所代表的所有坐标点所占用的空间。

请看下面的例子，矩阵可以缩减到只有一行。这表明原始 3x3 矩阵的秩为 1。

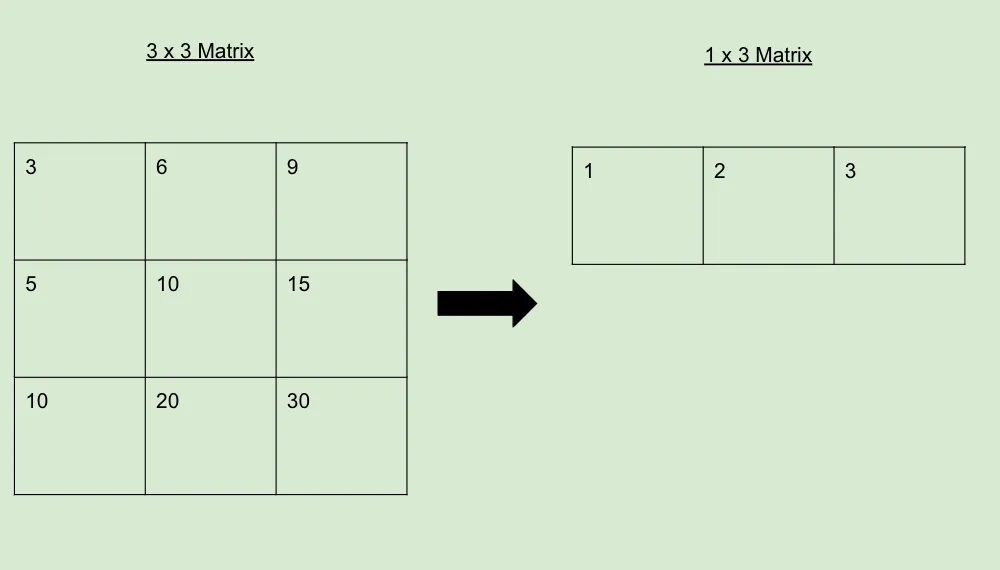
当一个矩阵可以像上面这样还原时，我们就说它的秩比不能像这样还原的矩阵低。任何秩较低的矩阵都可以像下面这样扩展回较大的矩阵，如下所示

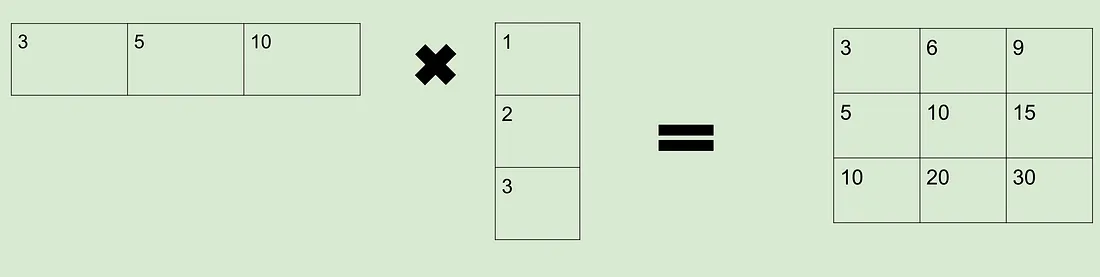
微调背景

要对模型进行微调，你需要一个高质量的数据集。例如，如果你想对汽车聊天模型进行微调，你需要一个包含数千条高质量汽车对话的数据集。

创建数据后，你需要将这些数据通过模型运行，以获得每个数据的输出结果。然后将该输出与数据集中的预期输出进行比较，并计算两者之间的差异。通常情况下，我们会使用交叉熵（突出显示两个概率分布之间的差异）这样的函数来量化这种差异。

现在我们利用损失来修改模型权重。我们可以认为这就像是创建了一个新的ΔW 矩阵，它包含了我们希望 Wo 矩阵知道的所有变化。我们获取权重，然后决定如何对其进行修改，以便在损失函数中得到更好的结果。我们通过反向传播来确定如何调整权重。

LoRA 方法

LoRA 围绕一个关键假设展开：虽然机器学习模型的权重矩阵秩较高，但微调过程中创建的权重更新内在秩较低。换句话说，我们可以使用比从头开始训练模型小得多的矩阵对模型进行微调，而且不会出现任何重大的性能损失。

因此，我们的基本方程是这样设置的：

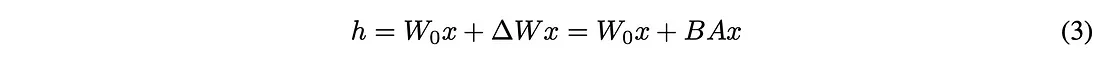
h 是微调后的权重值。Wo 和 ΔW 与之前的相同，但作者创建了一种新的方法来定义 ΔW。为了找到 ΔW，作者创建了两个矩阵：A 和 B： A 是一个与 Wo 具有相同列维的矩阵，开始时充满随机噪音，而 B 具有与 Wo 相同的行维，初始化为所有 0。这些维度非常重要，因为当我们将 A 和 B 相乘时，它们将创建一个与 ΔW 维度完全相同的矩阵。

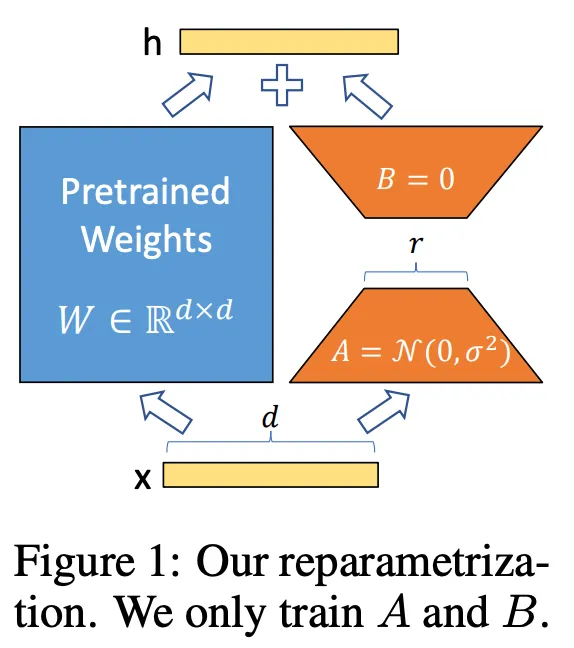
在微调过程中，A 和 B 的等级是一个超参数集。这意味着我们可以选择等级 1 来最大限度地加快训练速度（同时仍能改变 Wo），或者增加等级大小，从而以更大的代价提高性能。

使用 LoRA 进行微调

回到之前的图片，让我们看看使用 LoRA 时计算会发生哪些变化。

请记住，微调意味着创建 ΔW 矩阵，其中包含我们对 Wo 矩阵的所有更改。举个简单的例子，假设 A 和 B 的秩为 1，维数为 3：

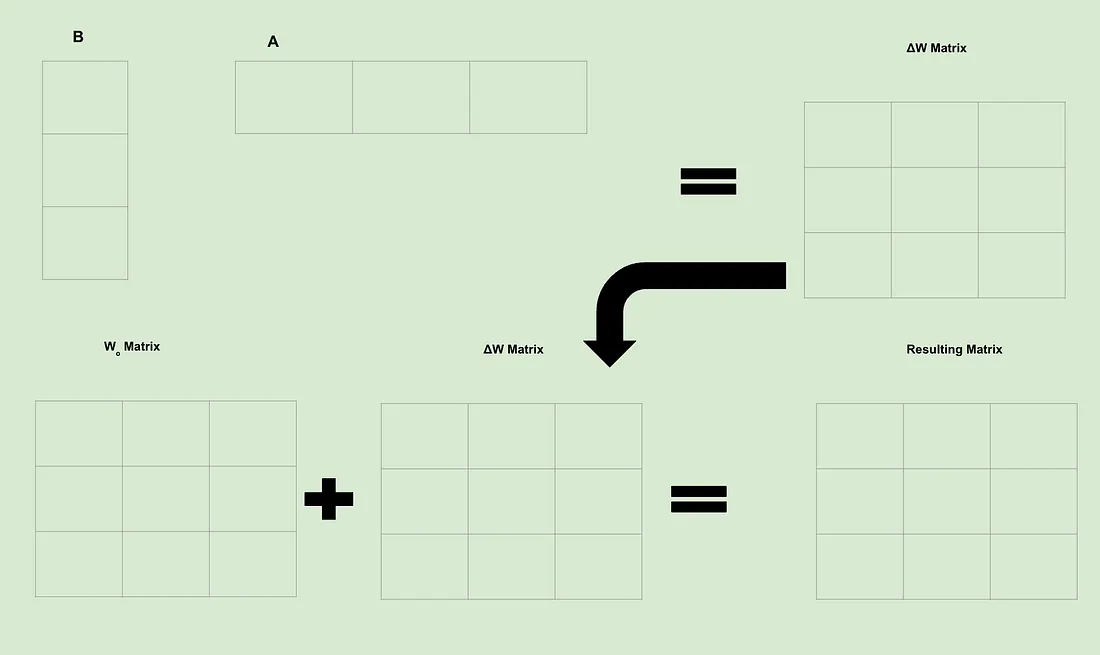
由于矩阵中的每个单元格都包含一个可训练权重，我们立即就能明白 LoRA 为何如此强大：我们从根本上减少了需要计算的可训练权重的数量。因此，虽然寻找单个可训练权重的计算量通常保持不变，但由于计算次数大大减少，我们节省了大量的计算量和时间。

结论

LoRA 已成为微调模型的行业标准方法。即使是拥有巨大资源的公司，也已认识到 LoRA 是改进其模型的一种经济有效的方法。