异常值检测是机器学习中的一项常见任务。具体来说，它是无监督机器学习的一种形式：分析没有标签的数据。它是指在数据集中找到相对于其他数据而言不寻常的项目。

希望识别数据中的异常值有很多原因。如果要检查的数据是会计记录，而我们又想找出错误或欺诈行为，那么数据中的交易通常太多，无法逐一进行人工检查，因此有必要选择少量可管理的交易进行调查。一个好的起点是找到最不寻常的记录并对其进行检查；这样做的前提是，错误和欺诈都应该足够罕见，以至于能够作为异常值脱颖而出。

也就是说，并不是所有的异常值都很有趣，但错误和欺诈很可能是异常值，因此在查找这些异常值时，识别异常值是一种非常实用的技术。

或者，数据可能包含信用卡交易、传感器读数、天气测量、生物数据或网站日志。在所有情况下，识别提示错误或其他问题的记录以及最有趣的记录都是非常有用的。

离群点检测通常也是商业或科学发现的一部分，用于更好地理解数据和数据中描述的过程。例如，对于科学数据，我们通常会对找出最不寻常的记录感兴趣，因为这些记录可能是最有科学意义的。

离群点检测中对可解释性的需求

对于分类和回归问题，通常最好使用可解释的模型。这样做可能会降低准确率（对于表格数据，通常使用提升模型的准确率最高，而这种模型是很难解释的），但也更安全：我们知道模型将如何处理未见数据。但是，在分类和回归问题中，通常也不需要理解为什么会做出这样的预测。只要模型相当准确，让它们进行预测就足够了。

但对于离群点检测，对可解释性的要求就高得多。如果离群点检测器预测某个记录非常不寻常，但又不清楚为什么会出现这种情况，我们可能就不知道该如何处理这个项目，甚至不知道是否应该相信它是异常的。

事实上，在很多情况下，如果不能很好地理解被标记为异常值的项目被标记的原因，那么进行异常值检测的价值就很有限。如果我们正在检查一个信用卡交易数据集，而异常值检测例程发现了一系列似乎极不寻常并因此可疑的购买行为，那么我们只有知道这些行为不寻常的原因，才能对其进行有效调查。在某些情况下，这可能是显而易见的，或者在花费一些时间进行检查后才会明白，但如果在发现异常时就清楚异常的性质，则会更加有效和高效。

与分类和回归一样，在无法解释的情况下，通常可以尝试使用所谓的事后解释来理解预测结果。这就需要使用 XAI（可解释的人工智能）技术，如特征导入、代理模型、ALE 图等。这些技术也非常有用，我们将在今后的文章中介绍。但是，首先获得清晰的结果也有很大的好处。

在本文中，我们将专门讨论表格数据。目前常用的表格数据离群值检测算法有很多，包括隔离森林、局部离群因子 (LOF)、KNN、单类 SVM 和其他许多算法。这些方法通常效果很好，但遗憾的是，大多数方法并不能对发现的离群值做出解释。

大多数离群值检测方法在算法层面上都很容易理解，但却很难确定为什么有些记录能得到检测器的高分，而另一些记录却不能。例如，如果我们使用隔离森林来处理金融交易数据集，我们可以看到哪些是最不寻常的记录，但可能不知道为什么，特别是如果表格有很多特征，如果离群值包含多个特征的罕见组合，或者离群值是没有特征高度不寻常，但多个特征中度不寻常的情况。

频繁模式离群因子 (FPOF)

现在，我们至少已经快速了解了异常值检测和可解释性。

FPOF（FP-outlier：基于频繁模式的离群点检测）是少数几个可以为离群点检测提供一定程度的可解释性的检测器之一，值得在离群点检测中更多地使用。

它还有一个吸引人的特点，就是设计用于分类数据而非数值数据。现实世界中的大多数表格数据都是混合数据，既包含数字列，也包含分类列。但是，大多数检测器都假定所有列都是数字列，要求所有分类列都进行数字编码（使用单数、序数或其他编码）。

如果检测器（如 FPOF）假定数据是分类数据，我们就会遇到相反的问题：所有数字特征都必须进行二进制处理，才能成为分类格式。两种方法都可行，但当数据主要是分类数据时，使用 FPOF 等检测器会比较方便。

而且，在进行离群点检测时，我们还可以同时使用数字检测器和分类检测器。遗憾的是，分类检测器相对较少，因此即使在不需要可解释性的情况下，FPOF 在这方面也很有用。

FPOF 算法

FPOF 的工作原理是在表格中识别所谓的 "常项集"（FIS）。它们要么是单个特征中非常常见的值，要么是跨越多个列且经常一起出现的值集。

几乎所有表格都包含大量的 FIS。只要列中的某些值比其他值更常见，就会出现基于单个值的 FIS，这种情况几乎总是存在。只要列之间存在关联，就会出现基于多列的 FIS：某些值（或数值范围）往往与其他列中的其他值（或数值范围）相关联。

FPOF 所基于的理念是，只要数据集有许多频繁项集（几乎所有数据集都有频繁项集），那么大多数行都会包含多个频繁项集，而且离群（正常）记录包含的频繁项集会明显多于离群行。我们可以利用这一点，将离群行识别为包含比大多数行少得多、频率低得多的频繁项集的行。

实际数据示例

我们以 OpenML 的 SpeedDating 数据集（https://www.openml.org/search?type=data&sort=nr_of_likes&status=active&id=40536，采用 CC BY 4.0 DEED 许可）作为使用 FPOF 的实际示例。

执行 FPOF 首先要挖掘数据集中的 FIS。Python 中有许多库可以支持这项工作。在本例中，我们使用 mlxtend (https://rasbt.github.io/mlxtend/)，它是一个机器学习的通用库。它提供了几种识别频繁项集的算法；我们在此使用了一种名为 apriori 的算法。

我们首先从 OpenML 收集数据。通常情况下，我们会使用所有的分类和（分选的）数字特征，但为了简单起见，这里我们只使用少量特征。

如前所述，FPOF 需要对数字特征进行分选。通常情况下，我们只需为每列数值特征使用少量（也许 5 到 20 个）等宽的二进制。为此，pandas cut() 方法非常方便。本例更加简单，因为我们只需处理分类列。

from mlxtend.frequent_patterns import apriori
import pandas as pd
from sklearn.datasets import fetch_openml
import warnings
warnings.filterwarnings(action='ignore', category=DeprecationWarning)
data = fetch_openml('SpeedDating', version=1, parser='auto') 
data_df = pd.DataFrame(data.data, columns=data.feature_names)
data_df = data_df[['d_pref_o_attractive', 'd_pref_o_sincere',
                   'd_pref_o_intelligence', 'd_pref_o_funny',
                   'd_pref_o_ambitious', 'd_pref_o_shared_interests']] 
data_df = pd.get_dummies(data_df) 
for col_name in data_df.columns:
    data_df[col_name] = data_df[col_name].map({0: False, 1: True})
frequent_itemsets = apriori(data_df, min_support=0.3, use_colnames=True) 
data_df['FPOF_Score'] = 0
for fis_idx in frequent_itemsets.index: 
    fis = frequent_itemsets.loc[fis_idx, 'itemsets']
    support = frequent_itemsets.loc[fis_idx, 'support'] 
    col_list = (list(fis))
    cond = True
    for col_name in col_list:
        cond = cond & (data_df[col_name])
           
    data_df.loc[data_df[cond].index, 'FPOF_Score'] += support   
min_score = data_df['FPOF_Score'].min() 
max_score = data_df['FPOF_Score'].max()
data_df['FPOF_Score'] = [(max_score - x) / (max_score - min_score) 
                         for x in data_df['FPOF_Score']]

apriori 算法要求对所有特征进行单次编码。为此，我们使用panda的 get_dummies() 方法。

然后，我们调用 apriori 方法来确定频繁项集。为此，我们需要指定最小支持度，即 FIS 出现的最小行数。我们不希望支持率过高，否则即使是强离群值，记录中包含的 FIS 也会很少，从而难以与异常值区分开来。我们也不希望这个值太低，否则 FIS 可能没有意义，离群值可能和异常值一样多。如果最小支持率过低，apriori 还可能生成大量的 FIS，从而导致执行速度变慢，可解释性降低。在本例中，我们使用 0.3。

对 FIS 的大小设置限制也是可能的，有时也会这样做，要求它们与某一最小和最大列数相关，这可能有助于缩小你最感兴趣的异常值的范围。

然后，频繁项集会以 pandas 数据帧的形式返回，数据帧中包含支持度列和列值列表（以单击编码列的形式，其中包含原始列和值）。

要解释结果，我们可以先查看 frequent_itemsets （下图所示）。为了包括每个 FIS 的长度，我们添加了：

frequent_itemsets['length'] = \
    frequent_itemsets['itemsets'].apply(lambda x: len(x))

共找到 24 个 FIS，最长的涵盖三个特征。下表列出了按支持率排序的前十行。

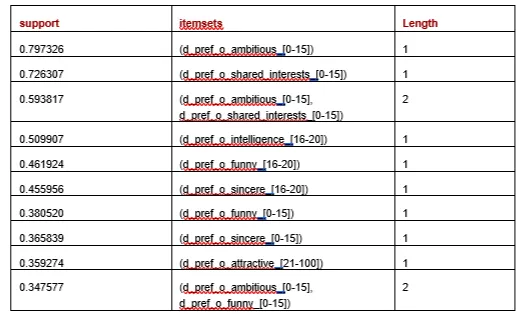
然后，我们循环查看每个频繁项集，并将包含频繁项集的每一行的得分按支持率递增。我们可以根据实际情况进行调整，使其更有利于长度更长的频繁项目集（例如，支持率为 0.4 且覆盖 5 列的频繁项目集，在其他条件相同的情况下，比支持率为 0.4 且覆盖 2 列的频繁项目集更相关），但在这里，我们只需使用每一行中频繁项目集的数量和支持率即可。

这实际上是对正态性而非离散性进行评分，因此当我们将评分归一化为 0.0 至 1.0 之间时，就会颠倒顺序。得分最高的行现在是最强的离群值：拥有最少和最不常见频繁项目集的行。

将分数列添加到原始数据帧并按分数排序，我们就能看到最正常的行：

我们可以看到，这一行的值与 FIS 非常吻合。d_pref_o_attractive 的值为 [21-100]，属于 FIS（支持度为 0.36）；d_pref___ambitious 和 d_pref_o_shared_interests 的值分别为 [0-15] 和 [0-15]，也属于 FIS（支持度为 0.59）。其他值也倾向于与 FIS 匹配。

接下来显示的是最不寻常的一行。它与所有已识别的 FIS 都不匹配。

由于频繁项目集本身非常容易理解，因此这种方法的优点是可以产生合理的可解释结果，但在使用许多频繁项目集的情况下，这种优点就不那么明显了。

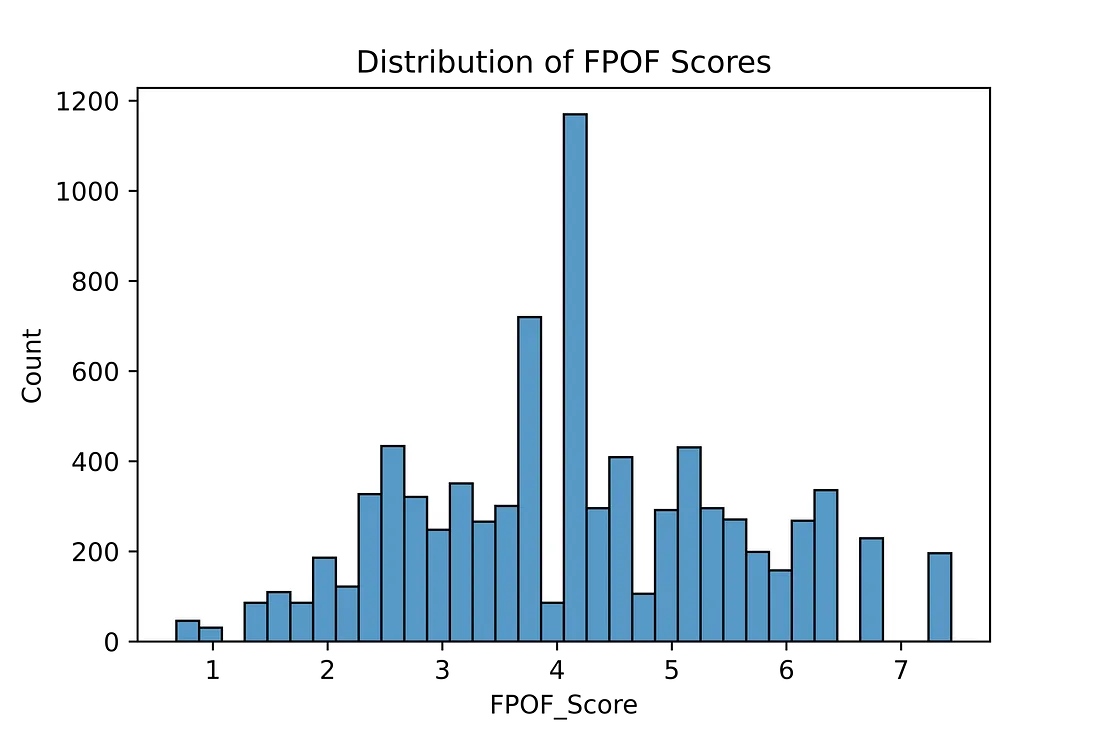
可解释性可能会降低，因为异常值不是根据是否包含 FIS 来识别的，而是根据是否不包含 FIS 来识别的，这意味着解释一行的得分相当于列出它不包含的所有 FIS。不过，严格来说，并没有必要列出所有缺失的 FIS 来解释每个异常值；列出一小部分最常见的缺失 FIS 就足以解释异常值，达到大多数目的的适当水平。对存在的 FIS 以及行中存在的 FIS 的正常数量和频率进行统计，可以很好地进行比较。

这种方法的一个变种是使用不常见的项目集，而不是常见的项目集，根据每一行所包含的每个不常见项目集的数量和罕见程度对每一行进行评分。这种方法也能得出有用的结果，但计算成本要高得多，因为需要挖掘更多的项目集，而且每一行都要根据许多 FIS 进行测试。不过，最终得分的可解释性更高，因为它们是基于在每一行中找到的项目集，而不是缺失的项目集。

结论

FPOF 的主要工作是挖掘 FIS，有许多 Python 工具可以实现这一点，包括本文使用的 mlxtend 库。如上所述，FPOP 的其余代码相当简单。