在当今的人工智能世界中，神经网络推动了无数的创新和进步。多层感知器（MLP）是许多突破的核心，它是一种以能够逼近复杂函数而著称的神经网络。

这是柯尔莫哥洛夫-阿诺德网络（Kolmogorov-Arnold Networks，KANs），一种受柯尔莫哥洛夫-阿诺德表示定理启发的神经网络新方法。与在每个神经元上使用固定激活函数的传统 MLP 不同，KAN 在网络边缘（权重）上使用可学习的激活函数。这一简单的转变在准确性、可解释性和效率方面开辟了新的可能性。

本文将探讨为什么 KAN 是神经网络设计的革命性进步。我们将深入探讨其数学基础，强调与 MLP 的主要区别，并展示 KAN 如何超越传统方法。

1: MLP 的局限性

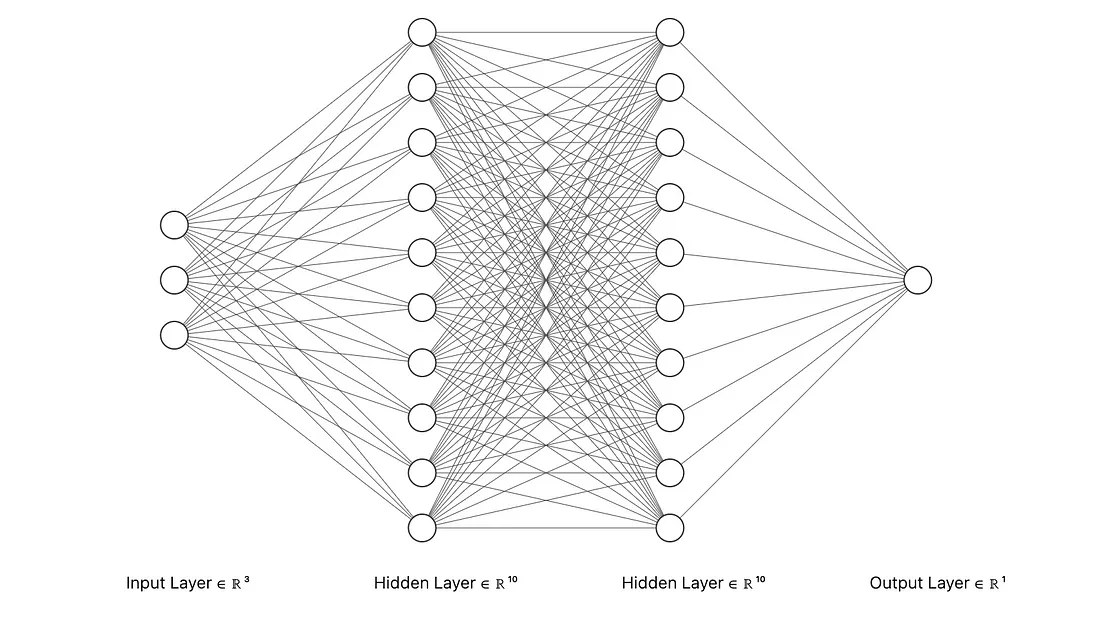
多层感知器（MLP）是现代神经网络的核心组成部分。它们由多层相互连接的节点或 "神经元 "组成，旨在通过从数据中学习来逼近复杂的非线性函数。每个神经元对其输入的加权和使用一个固定的激活函数，通过多层抽象将输入数据转化为所需的输出。MLP 推动了从计算机视觉到语音识别等多个领域的突破。

然而，MLP 也有一些明显的局限性：

1. 节点的固定激活函数： MLP 中的每个节点都有一个预先确定的激活函数，如 ReLU 或 Sigmoid。虽然在很多情况下都很有效，但这些固定函数限制了网络的灵活性和适应性。这使得 MLP 在优化某些类型的函数或适应特定数据特征时面临挑战。
2. 可解释性问题： MLP 经常被批评为 "黑盒子"。随着其变得越来越复杂，理解其决策过程也变得越来越困难。固定的激活函数和错综复杂的权重矩阵掩盖了网络的内部运作，如果不进行大量分析，就很难解释和相信模型的预测。

这些弊端凸显了人们对具有更大灵活性和可解释性的替代方案的需求，从而为像 Kolmogorov-Arnold 网络（KANs）这样的创新铺平了道路。

2: 柯尔莫格罗夫-阿诺德网络（KAN）

数学家安德烈-柯尔莫戈罗夫和弗拉基米尔-阿诺德提出的科尔莫戈罗夫-阿诺德表示定理指出，任何多元连续函数都可以表示为单变连续函数的有限组合和加法运算。把这个定理看作是把复杂的食谱分解成每个人都能遵循的简单步骤。你不用一次性处理整个食谱，而是分别处理每个步骤，从而使整个过程更易于管理。该定理意味着复杂的高维函数可以分解为更简单的单变量函数。

对于神经网络来说，这一见解是革命性的，它表明可以设计一个网络来学习这些单变量函数及其组成，从而提高准确性和可解释性。

KAN 通过从根本上改变神经网络的结构，充分利用了科尔莫哥罗德-阿诺德定理的力量。传统的 MLP 在每个节点上都应用固定的激活函数，而 KAN 则不同，它将可学习的激活函数放在网络的边缘（权重）上。这一关键区别意味着，KAN 网络在训练过程中会自适应地学习最佳的激活函数，而不是使用一组静态的激活函数。KAN 中的每条边都代表了一个参数化为样条曲线的单变量函数，允许根据数据进行动态和细粒度的调整。

这一变化增强了网络的灵活性和捕捉数据中复杂模式的能力，为传统的 MLP 提供了一个更可解释、更强大的替代方案。通过关注边缘上可学习的激活函数，KANs 有效地利用了科尔莫哥洛夫-阿诺德定理来改变神经网络设计，从而提高了各种人工智能任务的性能。

3：数学基础

柯尔莫哥洛夫-阿诺德网络（KAN）的核心是一组定义这些网络如何处理和转换输入数据的方程。KAN的基础在于柯尔莫哥洛夫-阿诺德表示定理，它启发了网络的结构和学习过程。

想象一下，你有一个输入向量 x=[x1,x2,...,xn]，它代表了你要处理的数据点。把这个输入向量想象成食谱的配料表。

该定理指出，任何复杂的配方（高维函数）都可以分解成更简单的步骤（单变量函数）。对于 KAN 来说，每种成分（输入值）都会通过网络边缘上的一系列简单步骤（单变量函数）进行转换。数学上可以表示为：

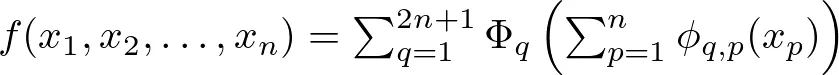
这里，ϕ_q,p 是在训练过程中学习到的单变量函数。将 ϕ_q,p 视为每种食材的单独烹饪技术，而 Φ_q 则是将这些准备好的食材组合起来的最终组装步骤。

KAN 的每一层都应用这些烹饪技术对食材进行进一步的转换。对第 l 层来说，变换的公式如下：

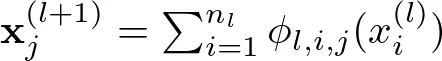
这里，x(l) 表示第 l 层的转化食材，j_l,i,j 是第 l 层和第 l+1 层之间边缘上的可学习单变量函数。这就好比在每一步对食材应用不同的烹饪技术，从而得到中间菜肴。

KAN 的输出是这些层变换的组合。就像把中间菜肴组合在一起才能做出最后的菜肴一样，KAN 将变换组合在一起才能产生最终的输出结果：

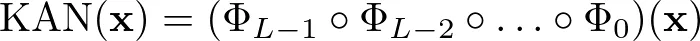
这里，Φl 代表第 l 层的单变量函数矩阵。KAN 的整体功能由这些层组成，每一层都会进一步细化转换。

MLP 结构

在传统的 MLP 中，每个节点对其输入应用一个固定的激活函数（如 ReLU 或 sigmoid）。这就好比对所有食材使用相同的烹饪技巧，而不管其性质如何。

MLP 使用线性变换，然后是这些固定的非线性激活：

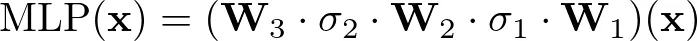
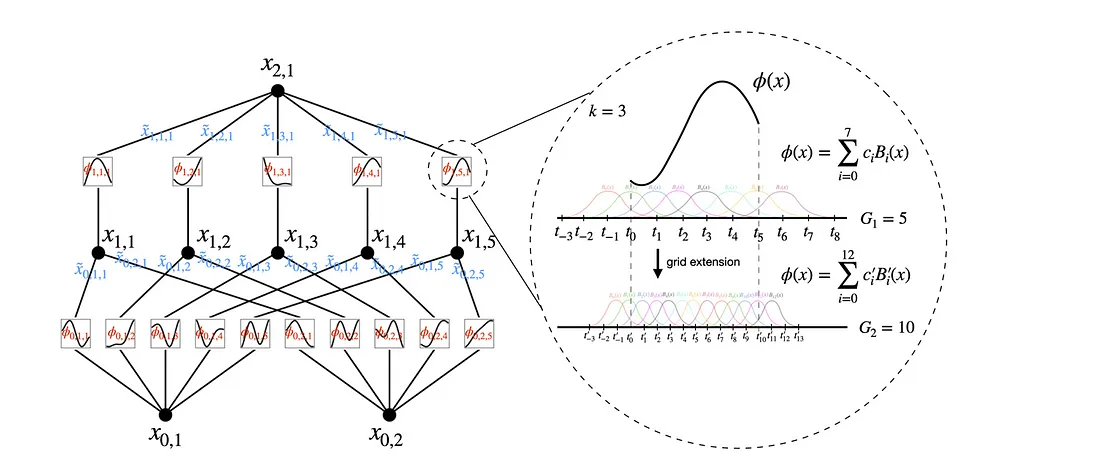
其中，W 代表权重矩阵，σ 代表固定激活函数。

网格扩展技术

网格扩展是一种功能强大的技术，它通过完善定义单变量函数的样条网格来提高柯尔莫哥洛夫-阿诺德网络（KAN）的准确性。这一过程允许网络学习数据中越来越详细的模式，而无需完全重新训练。

这些 B-样条曲线是一系列多项式函数，通过拼凑形成一条平滑的曲线。它们在 KAN 中用于表示边缘上的单变量函数。样条曲线定义在一系列称为网格点的区间上。网格点越多，样条曲线所能捕捉的细节就越精细

最初，网络从粗网格开始，这意味着网格点之间的间隔较少。这样，网络就能了解数据的基本结构，而不会被细节所困扰。这就好比在填充细节之前，先勾勒出一个粗略的轮廓。

随着训练的进行，网格点的数量会逐渐增加。这个过程被称为网格细化。通过添加更多的网格点，样条曲线变得更加细致，可以捕捉到数据中更精细的模式。这类似于在最初的草图上逐步增加细节，将其变成一幅详细的图画。

每次增加都会引入新的 B 样条曲线基函数 B′_m(x)。对这些新基函数的系数 c'_m 进行调整，以确保新的、更细的样条曲线与原始的、更粗的样条曲线紧密匹配。

为了实现这种匹配，我们使用了最小二乘优化法。这种方法通过调整系数 c'_m 来最小化原始样条曲线与细化样条曲线之间的差异。

从根本上说，这一过程可确保细化样条线继续准确地表示粗样条线所了解的数据模式。

简化技术

为了提高 KAN 的可解释性，可以采用几种简化技术，使网络更易于理解和可视化。

稀疏化和剪枝

这种技术是根据激活函数的 L1 准则为损失函数添加惩罚。函数 ϕ 的 L1 规范定义为该函数在所有输入样本中的平均值：

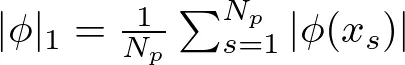
这里，N_p 是输入样本的数量，j(x_s) 表示输入样本 x_s 的函数 ϕ 值。

把稀疏化想象成整理房间。通过删除不必要的项目（或减少不那么重要的函数的影响），可以使空间（或网络）更有条理，更容易浏览。

应用 L1 正则化后，会对激活函数的 L1 规范进行评估。如果神经元和边的规范值低于某个阈值，就会被视为不重要，并被剪除。修剪阈值是一个超参数，决定了修剪的力度。

修剪就像修剪一棵树。剪掉弱枝和不必要的枝条，就能让树把资源集中到更强壮、更重要的部分，从而使结构更健康、更易于管理。

符号化

另一种方法是用已知的符号形式取代已学的单变量函数，使网络更易于解释。

我们的任务是找出可以近似所学函数的潜在符号形式（如 sin、exp）。这一步骤包括分析已学函数，并根据其形状和行为提出候选符号。

一旦确定了候选符号，就可以使用网格搜索和线性回归来拟合参数，从而使符号函数近似于所学函数。

4：Python 中的 KAN 与 MLP 比较

为了展示 Kolmogorov-Arnold 网络（KAN）与传统的多层感知器（MLP）相比的能力，我们将把一个函数生成的数据集同时拟合到 KAN 模型和 MLP 模型上（利用 PyTorch），看看它们的性能如何。

我们将使用的函数与论文作者用来展示 KAN 与 MLP 能力的函数相同（原始论文示例）。不过，代码会有所不同。

让我们导入所需的库，并生成数据集

import numpy as np
import torch
import torch.nn as nn
from torchsummary import summary
from kan import KAN, create_dataset
import matplotlib.pyplot as plt

在这里，我们使用：

• numpy： 进行数值运算。
• torch： 用于构建和训练神经网络的 PyTorch。
• torch.nn： 用于 PyTorch 中的神经网络模块。
• torchsummary： 用于总结模型结构。
• kan： 包含 KAN 模型和数据集创建函数的自定义库。
• matplotlib.pyplot： 用于绘图和可视化。

# Define the dataset generation function
f = lambda x: torch.exp(torch.sin(torch.pi * x[:, [0]]) + x[:, [1]] ** 2)

该函数包含正弦（sin）和指数（exp）成分。它接收二维输入 x，并使用公式计算输出：

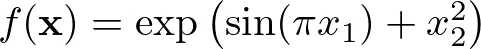
现在，让我们将均匀分布在 [-2, 2] 之间的 100 个点的张量拟合到这个函数中，看看它是什么样子的：

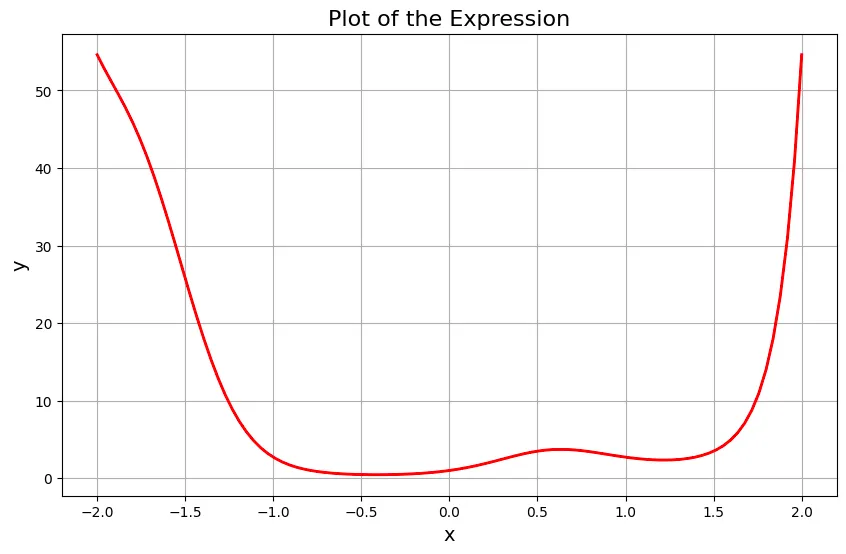
# Create the dataset
dataset = create_dataset(f, n_var=2)

数据集包括用于训练和测试神经网络的输入输出对。

现在，让我们建立一个 KAN 模型，并在数据集上对其进行训练。

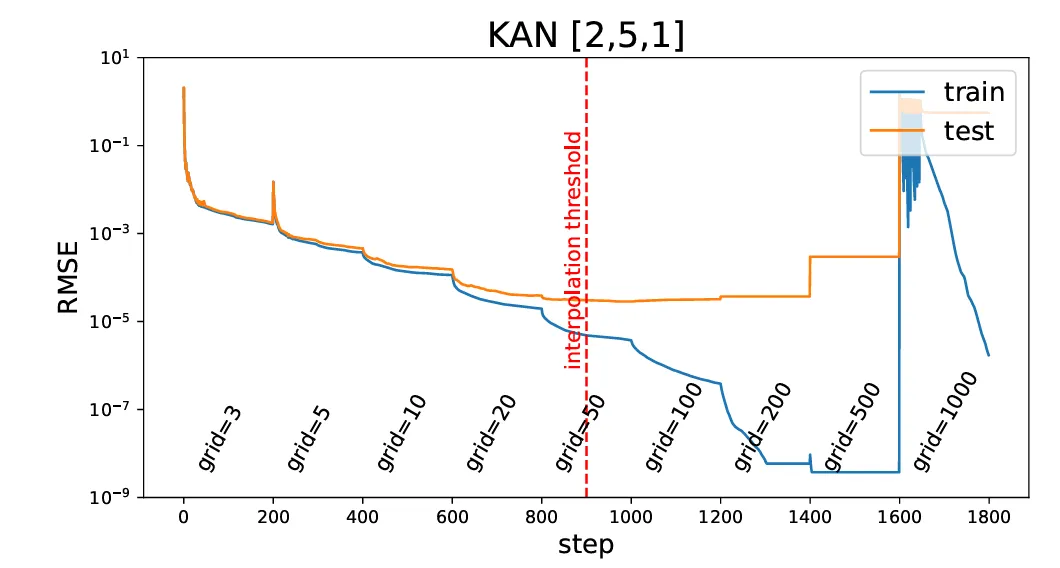
我们将从粗网格（5 个点）开始，逐渐细化网格（最多 100 个点）。这样可以捕捉到数据中更精细的细节，从而提高模型的准确性。

grids = np.array([5, 10, 20, 50, 100])
train_losses_kan = []
test_losses_kan = []
steps = 50
k = 3
for i in range(grids.shape[0]):
    if i == 0:
        model = KAN(width=[2, 1, 1], grid=grids[i], k=k)
    else:
        model = KAN(width=[2, 1, 1], grid=grids[i], k=k).initialize_from_another_model(model, dataset['train_input'])
    results = model.train(dataset, opt="LBFGS", steps=steps, stop_grid_update_step=30)
    train_losses_kan += results['train_loss']
    test_losses_kan += results['test_loss']
    print(f"Train RMSE: {results['train_loss'][-1]:.8f} | Test RMSE: {results['test_loss'][-1]:.8f}")

在本例中，我们定义了一个名为网格的数组，其值为 [5、10、20、50、100]。我们在这些网格上迭代，依次拟合模型，这意味着每个新模型都使用前一个模型进行初始化。

每次迭代，我们都定义一个 k=3 的模型，其中 k 是 B-样条曲线的阶数。我们将训练步数（或历时）设为 50。模型的结构包括一个有 2 个节点的输入层、一个有 1 个节点的隐藏层和一个有 1 个节点的输出层。我们使用 LFGBS 优化器进行训练。

以下是训练过程中的训练损失和测试损失：

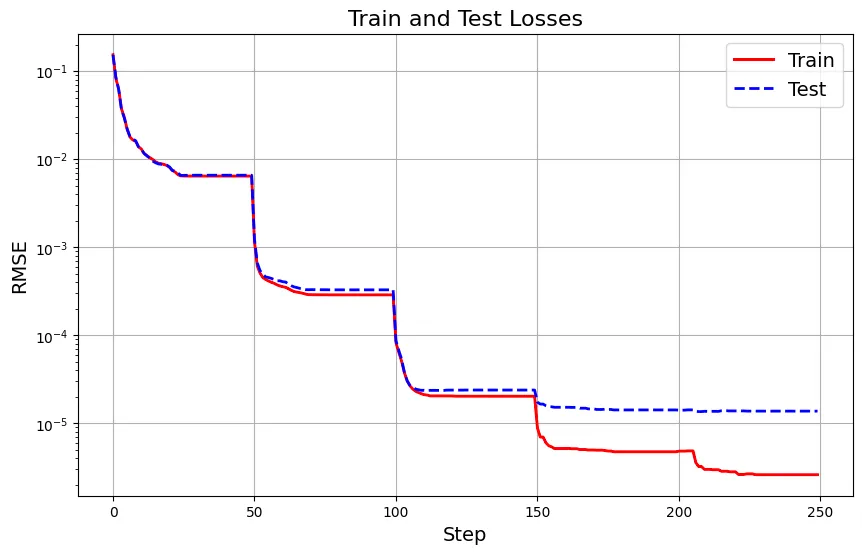
现在，让我们定义并训练一个传统的 MLP 以作比较。

# Define the MLP
class MLP(nn.Module):
    def __init__(self):
        super(MLP, self).__init__()
        self.layers = nn.Sequential(
            nn.Linear(dataset['train_input'].shape[1], 64),
            nn.ReLU(),
            nn.Linear(64, 64),
            nn.ReLU(),
            nn.Linear(64, 1)
        )
    def forward(self, x):
        return self.layers(x)
# Instantiate the model
model = MLP()
summary(model, input_size=(dataset['train_input'].shape[1],))

MLP 有一个输入层、两个各有 64 个神经元的隐藏层和一个输出层。各层之间使用 ReLU 激活。

criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=1e-2)
train_loss_mlp = []
test_loss_mlp = []
epochs = 250
for epoch in range(epochs):
    optimizer.zero_grad()
    output = model(dataset['train_input']).squeeze()
    loss = criterion(output, dataset['train_label'])
    loss.backward()
    optimizer.step()
    train_loss_mlp.append(loss.item()**0.5)
    # Test the model
    model.eval()
    with torch.no_grad():
        output = model(dataset['test_input']).squeeze()
        loss = criterion(output, dataset['test_label'])
        test_loss_mlp.append(loss.item()**0.5)
    print(f'Epoch {epoch+1}/{epochs}, Train Loss: {train_loss_mlp[-1]:.2f}, Test Loss: {test_loss_mlp[-1]:.2f}', end='\r')

我们使用均方误差 (MSE) 损失和 Adam 优化器，对模型进行了 250 次历时训练，并记录了训练和测试损失。

这就是 MLP 的训练和测试均方根误差：

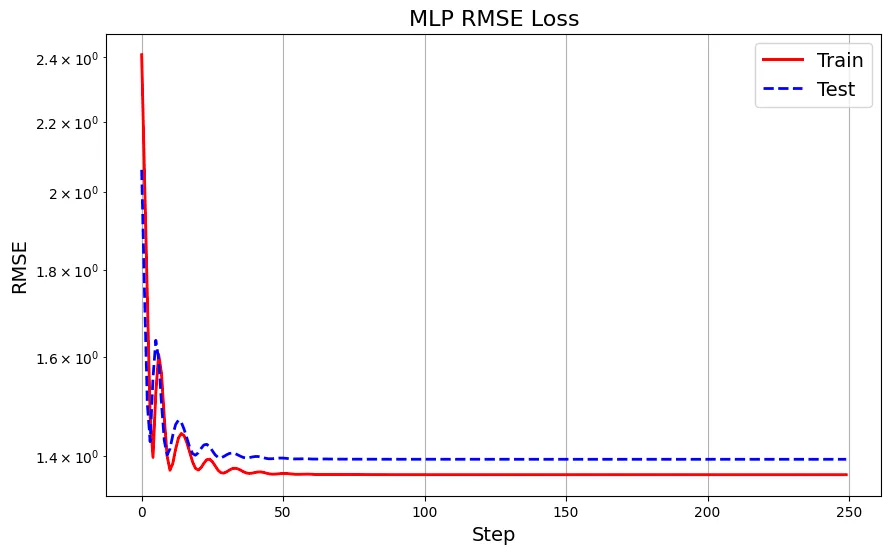
让我们把损失图并列起来比较一下：

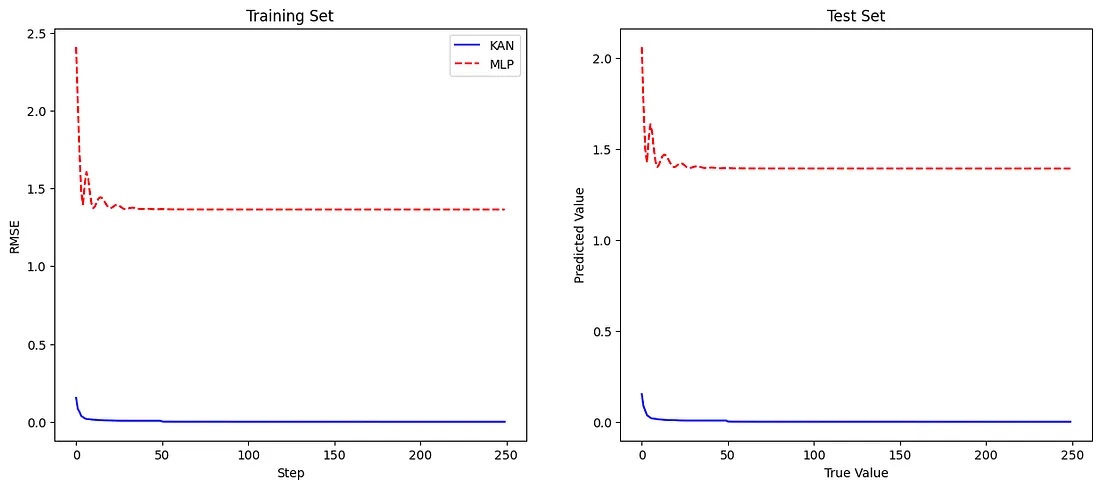
从图中可以看出，KAN 模型的训练均方根误差（RMSE）低于 MLP 模型，这表明 KAN 模型具有更好的函数拟合能力。同样，KAN 模型在测试集上的表现也优于 MLP，显示出其卓越的泛化能力。

这个例子说明了 KAN 如何利用其灵活的自适应结构，比传统的 MLP 更准确地拟合复杂函数。通过细化网格并在边缘采用可学习的单变量函数，KANs 可以捕捉到 MLP 可能会忽略的数据中的复杂模式，从而提高函数拟合任务的性能。

5: KAN的优势

准确性

与传统的多层感知器（MLP）相比，Kolmogorov-Arnold 网络（KANs）的突出优势之一是能以更少的参数获得更高的精度。这主要归功于边缘上的可学习激活函数，它使 KAN 能够更好地捕捉数据中的复杂模式和关系。

与在每个节点上使用固定激活函数的 MLP 不同，KAN 在边缘上使用单变量函数，这使得网络更加灵活，能够根据数据对其学习过程进行微调。

由于 KAN 可以动态调整各层之间的函数，因此它们可以用较少的参数达到相当甚至更高的精度。这种效率对于数据或计算资源有限的任务尤为有利。

可解释性

与传统的 MLPs 相比，KANs 在可解释性方面有显著提高。这种增强的可解释性对于理解决策过程和结果同样重要的应用至关重要。

KAN 可以通过稀疏化和剪枝等技术进行简化，从而去除不必要的函数和参数。这些技术不仅能提高可解释性，还能通过关注最相关的部分来提高网络的性能。

对于某些函数，可以识别激活函数的符号形式，从而更容易理解网络内的数学变换。

可扩展性

与 MLP 相比，KAN 表现出更快的神经扩展规律，这意味着随着参数数量的增加，KAN 的改进速度会更快。

由于 KAN 能够将复杂的函数分解为更简单的单变量函数，因此它们能受益于更有利的扩展规律。与 MLP 相比，随着模型复杂度的增加，KANs 可以更有效地降低误差率。

KAN 可以从较粗的网格开始，在训练过程中扩展到较细的网格，这有助于平衡计算效率和准确性。这种方法使 KAN 比 MLP 更容易扩展，因为 MLP 在增加模型规模时往往需要完全重新训练。

结论

Kolmogorov-Arnold 网络（KANs）是传统多层感知器（MLPs）的突破性替代品，它提供了几项关键创新，解决了其前辈的局限性。通过利用边缘上的可学习激活函数而不是节点上的固定函数，KANs 将灵活性和适应性提升到了一个新的水平。这一结构性变化带来了：

• 更高的精度： KAN 以更少的参数实现更高的准确性，使其在各种任务中更加高效和有效。
• 提高可解释性： 可视化和简化 KAN 的能力有助于理解决策过程，这对医疗保健、金融和自主系统中的关键应用至关重要。
• 更好的可扩展性： KAN 展现出更快的神经扩展规律，使其能够比 MLP 更从容地处理不断增加的复杂性。