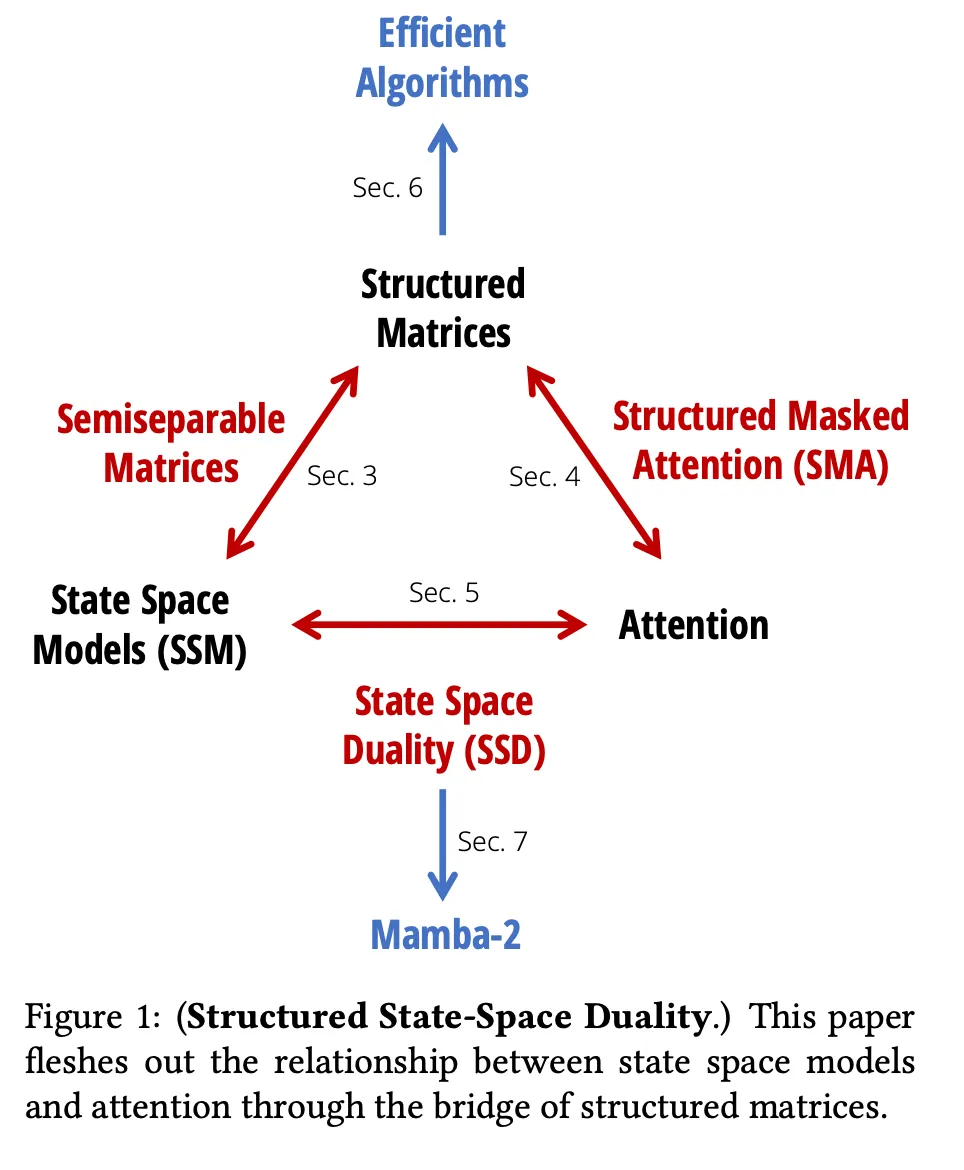
了解Mamba和选择性状态空间模型 (SSM)
状态空间模型
你可能首先会问:状态空间模型 (SSM) 到底是什么?其基本思想是模拟随时间变化的系统。为了实现这一点,我们可以选择与系统各部分 (A、B、C) 相对应的值,这些值在每次迭代中保持不变。然后,我们有 3 个向量表示系统如何变化 — h(状态向量)、x(输入向量)和 y(输出向量),其中 h' 是状态向量的下一次迭代。其关键思想是,我们在每一轮中都有新的t和h值,但 AB 和 C 保持不变。基本方程如下所示:

此外,由于 A、B 和 C 本身不会随时间而变化,SSM 通常在底层使用卷积——将相同的内核应用于输入序列的每个部分——在推理和训练期间实现高性能计算。
这些模型历史上曾用于信号处理、经济学和控制系统,然而,对于涉及离散数据(如文本)的任务,它们的用处不大。
选择性状态空间模型
为了解决离散数据问题,作者引入了 SSM 的新版本,称为选择性状态空间模型。这与典型的 SSM 有两大变化。首先,他们引入了一种选择机制,可以帮助我们过滤掉或关注某些数据。其次,由于选择机制,我们不能再使用卷积——因此,引入了选择性扫描。
遴选机制
从选择机制开始,作者通过将 B、C 和 Δ 更改为随时间变化(意味着它们现在根据t而变化)赋予模型选择数据的能力。 以下是 SSM(S4)和选择状态空间模型的典型实现:

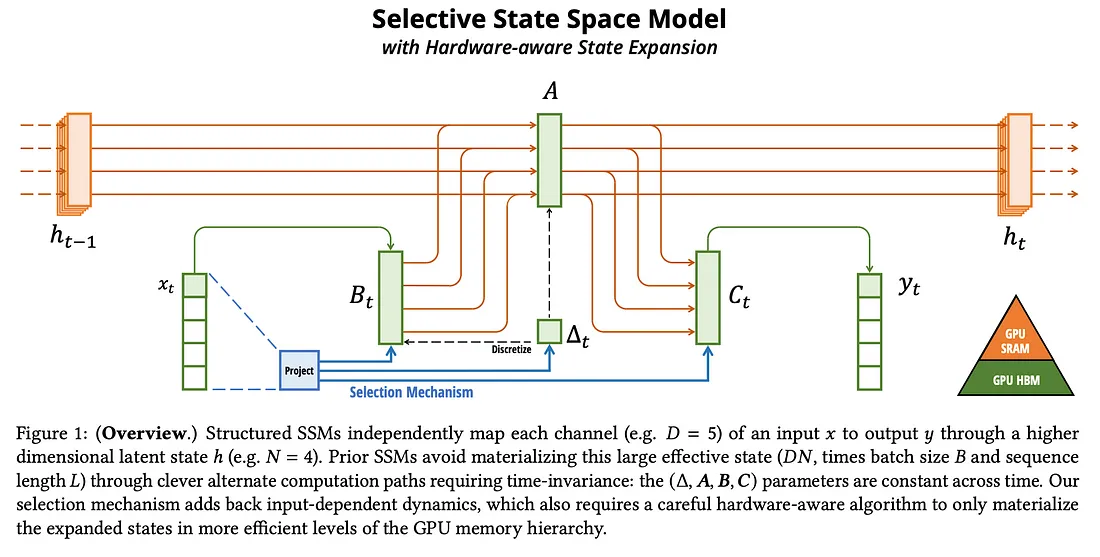
首先解释一下变量,x和y是具有维度 B(表示批处理大小)、L(表示序列长度)和 D(表示维度大小)的张量。N 被选为任意值,用于确定后续张量的大小。Δ 是我们用于从当前状态 h 过渡到下一个状态 h' 的张量。Sb 、Sc和SΔ 是激活函数(具体而言,Sb(x)=LinearN(x) Sc(x)=LinearN(x) Sd(x)=BroadcastD(Linear1(x)) Td = Softplus其中),离散LinearN is a linear projection to the N dimension化是将矩阵或张量从连续时间更改为离散时间。
退一步来说,主要的变化是输入元素。在算法 1 中,我们处理的是矩阵,而在算法 2 中,我们有 B、C 和 Δ 的张量。额外的维度来自于在输入张量x上运行我们的激活函数并将其放入相应的张量中。之前,B 和 C 传递了它们的所有信息,现在模型可以确定哪些信息是相关的,并只保留这些信息。由于对 x 有了新的依赖,算法 2 现在随时间(或输入)而变化。
这也许是与典型的 Transformer 相比最大的变化——我们不再采用自我注意力,而是采用选择机制来确定模型应该关注什么。
选择性扫描
由于 B 和 C 输入变体的存在,我们无法再使用卷积。为了解决这个问题,作者创建了一种“选择性扫描”算法,目标是通过硬件感知来获得更好的性能。
从图形处理单元 (GPU) 的角度来看,平衡在于数据和速度之间。高带宽内存 (HBM) 有大量空间来保存数据,但速度较慢。静态随机存取存储器 (SRAM) 速度很快,但无法保存大量数据。
要理解选择性扫描,我们首先要理解应用于选择性 SSM 的标准扫描操作。为此,我们需要将形状 (B、L、D、N) 的整个数据放入 HBM,因为 SRAM 无法处理这种大小的数据。然后,我们将扫描操作的计算应用于 HBM 中张量的每个部分,这会浪费大量时间在内存中的地址之间移动数据。
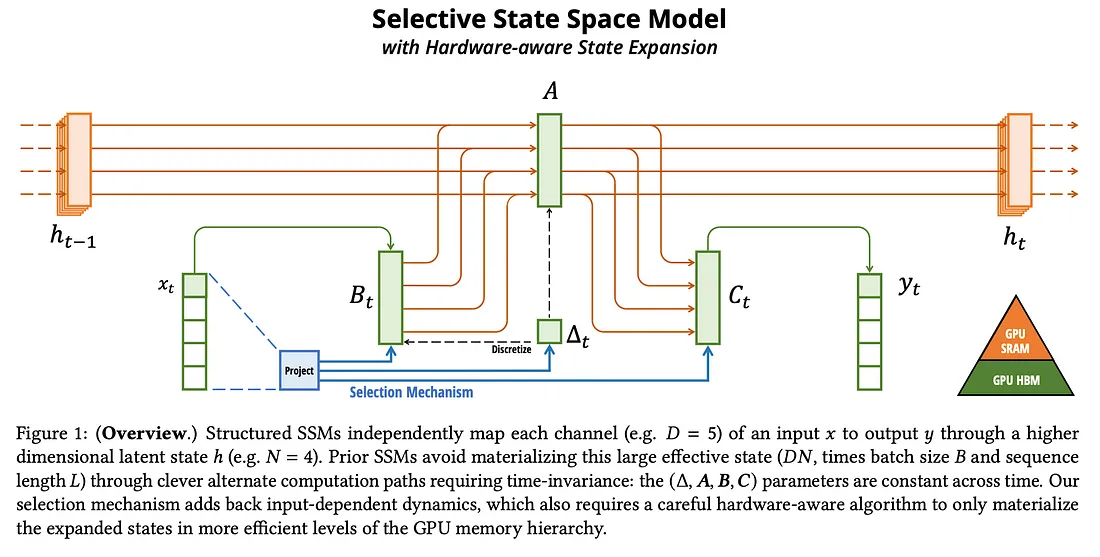
相比之下,选择性扫描的内存效率更高。它不会获取形状为 (B,L,D,N) 的整个数据,而是仅对形状分别为 (D, N) 和 (B, L, N) 的更新 (A, B, C, Δ) 进行操作。由于我们操作的数据明显较小,因此我们能够在 SRAM 中保存更多数据,从而大大缩短计算时间。计算完成后,大小为 (B, L, D) 的输出将输出到 y。上图显示了每个变量在 GPU 内存中的存储位置。
当你想要进行反向传递时,选择性扫描的最大弊端就出现了。由于内存中没有任何中间计算,因此我们需要重新计算这些计算,因此本质上是用计算换取内存。
Mamba 区块结构
现在我们了解了 SSM,我们可以看到如何使用它们来创建 Mamba 架构。
依靠两种块设计来创建 Mamba:Hungry, Hungry Hippos (H3) 和门控多层感知器 (Gated MLP)。由于 Mamba 结合了两者,让我们来解释一下这些块结构各自的工作原理。
多层感知器 (MLP) 在神经网络架构中极为常见。它们是前馈神经网络,其中每一层中的每个神经元都与前一层中的每个神经元相连。门控 MLP 的门控部分只是通过重置门和更新门对信息流进行了进一步的控制。重置门决定丢弃多少信息,而更新门决定现在应该传递多少来自输入和隐藏层的信息。
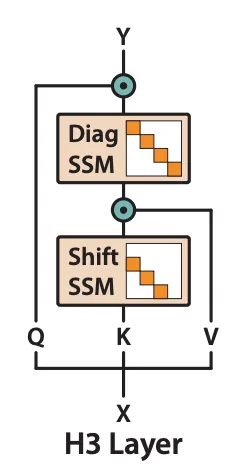
H3 是关于使用 SSM 记住先前的标记,然后将此结果与其他向量相乘以进行比较。为了分解它,我们首先将输入投影到熟悉的 Key、Value 和 Query 向量中。Key 值经过“移位”SSM,旨在提供一些先前标记的记忆。然后将输出与 Value 标记相乘,以便我们对标记进行第一次比较。然后我们运行“对角线”SSM 以在整个序列中传播这些标记交互。我们以查询乘法结束,以便我们可以将查询中存储的交互与当前元素进行比较。
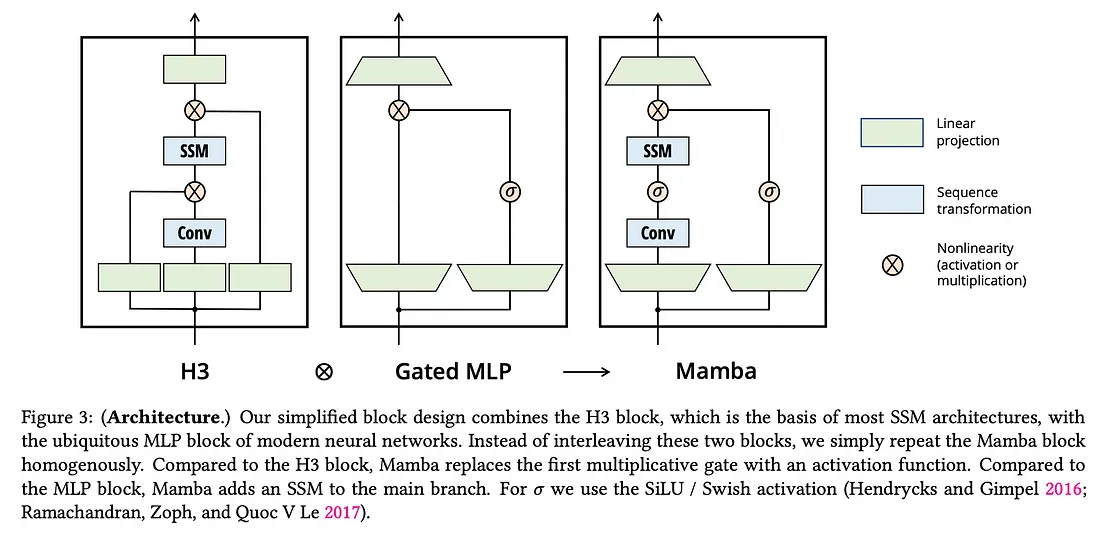
Mamba 采用了 Gated MLP 的门控功能,然后将其与卷积和选择性 SSM 变换相结合。请注意,虽然选择性 SSM 不再能在后台使用卷积来计算,但 Mamba 块中没有理由不能包含卷积。从高层次来看,我们现在有了一个新的块结构,它可以通过门控机制传递输入的某些部分,然后通过选择性 SSM 关注该输入的某些部分。下面将讨论上述的一些后果。
Mamba 推理时间
利用新的块架构,我们能够在训练和推理时间方面取得显著的改善。
首先,因为我们没有进行注意力机制,所以我们不必担心输入规模变大带来的二次方缩放。如果你回到论文中的图 1,你会看到,无论输入长度如何,传递的状态大小都是相同的。因此,虽然输入长度越大需要计算量越大,但它只会以线性速率增加。这与注意力机制形成对比,随着输入的增加,注意力模式的大小将呈二次方增长。这种线性与二次方缩放意味着,在其他条件相同的情况下,SSM 的训练和推理成本和延迟将大大优于 Transformers。
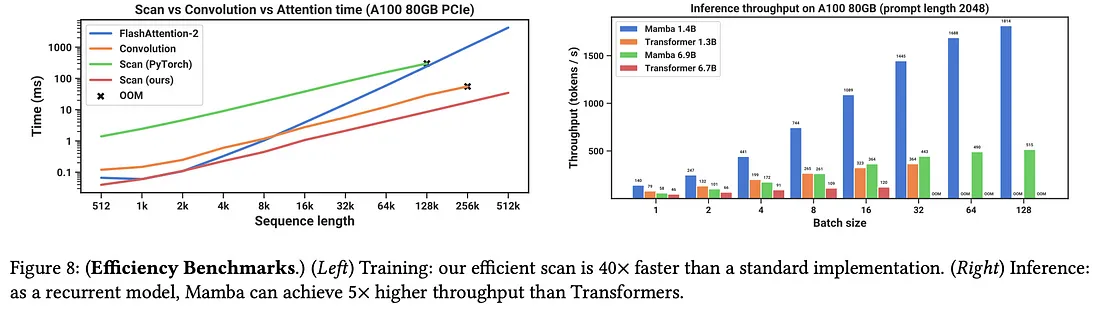
从下图中我们可以看出,Mamba 在恒定提示长度下的推理吞吐量明显高于类似复杂度的 Transformer 模型。事实上,随着批处理大小的增加,架构之间的差异会大大增加。
Mamba-2