在本文中，我们将探讨测试和评估离群值检测器这一众所周知的难题，并介绍一种有时被称为掺杂的解决方案。使用掺杂法，真实数据行（通常）被随机修改，但修改的方式要确保它们在某些方面可能是离群值，因此应该被离群值检测器检测到。这样，我们就可以通过评估检测器对掺杂记录的检测能力，对其进行评估。

在本文中，我们将特别关注表格数据，但同样的想法也可应用于其他模式，包括文本、图像、音频、网络数据等。

测试和评估其他类型的模型

如果你熟悉离群点检测，那么你可能也熟悉（至少在某种程度上）用于回归和分类问题的预测模型。对于这些类型的问题，我们都有标注过的数据，因此在调整模型（选择最佳的预处理、特征、超参数等）时，评估每个选项都相对简单；估计模型的准确性（模型在未见过的数据上的表现）也相对容易：我们只需使用训练-验证-测试拆分法，或者更好的交叉验证法。由于数据是有标签的，我们可以直接看到模型在有标签的测试数据上的表现。

但是，在离群点检测中，由于没有标注数据，问题就更加棘手了；我们没有客观的方法来确定离群点检测中得分最高的记录实际上是否是数据集中统计上最不寻常的记录。

再以聚类为例，我们也没有数据标签，但至少可以衡量聚类的质量：我们可以确定聚类的内部一致性如何，以及聚类之间的差异有多大。利用某种距离度量（如曼哈顿距离或欧氏距离），我们可以衡量一个聚类中记录之间的距离有多近，以及聚类之间的距离有多远。

再以聚类为例，我们也没有数据标签，但至少可以衡量聚类的质量：我们可以确定聚类的内部一致性如何，聚类之间的差异有多大。利用某种距离度量（如曼哈顿距离或欧氏距离），我们可以衡量一个聚类中记录之间的距离有多近，以及聚类之间的距离有多远。

因此，给定一组可能的聚类，就可以定义一个合理的度量（如剪影得分），并确定哪一个是首选聚类，至少就该度量而言是如此。也就是说，就像预测问题一样，我们可以为每个聚类计算一个分数，然后选择看起来效果最好的聚类。

但在离群点检测中，我们却没有类似的方法可以使用。任何试图量化记录异常程度的系统，或试图在给定两条记录的情况下确定哪条记录更异常的系统，其本身实际上就是一种离群点检测算法。

例如，我们可以使用熵作为离群值检测方法，然后可以检查整个数据集的熵，以及删除任何被识别为强离群值的记录后数据集的熵。这在某种意义上是正确的；熵是衡量是否存在异常值的有用指标。但我们不能假定熵就是这个数据集中离群值的明确定义；离群值检测的基本特征之一就是离群值没有明确的定义。

一般来说，如果我们有任何方法来试图评估离群值检测系统检测出的离群值（或者像上一个例子那样，有已识别离群值和没有已识别离群值的数据集），那么这本身实际上就是一个离群值检测系统，用它来评估所发现的离群值就成了循环论证。

因此，要评估离群值检测系统是相当困难的，而且实际上也没有很好的方法来评估离群值检测系统，至少使用现有的真实数据是如此。

不过，我们可以创建合成测试数据（我们可以假设合成数据主要是离群值）。这样，我们就能确定离群值检测器在多大程度上倾向于对合成记录进行比真实记录更高的评分。

掺杂数据记录

掺杂数据记录是指对现有数据记录稍作修改，通常只改变每条记录中一个或少数单元格的值。

例如，如果要检查的数据是一个由特许经营地点组成的公司财务状况表，我们可能会为每个特许经营地点设置一行，而我们的目标可能是找出其中最异常的记录。比方说，我们的特征包括：

• 特许经营店的年龄
• 当前所有者的经营年限
• 去年的销售数量
• 去年销售总额

以及其他一些特征。

一个典型的记录可能包含这四个特征的值，例如 20 年历史、与现任所有者共事 5 年、去年的独特销售额为 10,000 美元、去年的总销售额为 500,000 美元。

我们可以通过将某个值调整为稀有值来创建该记录的掺杂版本，例如，将特许经营权的年龄设置为 100 年。这可以做到，而且可以对被测检测器进行快速烟雾测试--任何检测器都有可能将其识别为异常值（假设 100 的值是罕见值），尽管我们可能会排除一些无法可靠检测到此类修改记录的检测器。

我们不必考虑离群点检测器的类型（如 kNN、熵或隔离林）本身，而是要考虑离群点检测器的类型、预处理、超参数和检测器的其他属性的组合。例如，我们可能会发现使用某些超参数的 kNN 检测器效果很好，而使用其他超参数的检测器则效果不佳（至少对于我们测试的掺杂记录类型而言）。

不过，通常情况下，大多数测试都会产生更微妙的异常值。在这个例子中，我们可以将总销售额的美元值从 500,000 改为 100,000，这可能仍然是一个典型值，但对于这个数据集来说，10,000 个唯一销售额与 100,000 美元总销售额的组合很可能是不寻常的。也就是说，在使用兴奋剂的过程中，我们经常会创建一些具有不寻常值组合的记录，尽管有时也会创建不寻常的单一值。

在更改记录中的某个值时，我们并不清楚该行将如何成为异常值（假设它真的成为了异常值），但我们可以假设大多数表格的特征之间存在关联。在这个例子中，如果将美元值改为 100,000，很可能（除了会产生销售数量和销售美元值的不寻常组合外）还会根据特许经营权的年限或当前所有者的年限产生不寻常的组合。

然而，有些表格中的特征之间没有关联，或者关联很少而且很弱。这种情况很少见，但也有可能发生。对于这类数据，没有不寻常值组合的概念，只有不寻常的单一值。这种情况虽然罕见，但处理起来其实更简单：更容易检测异常值（我们只需检查单个异常值），也更容易评估检测器（我们只需检查单个异常值的检测能力）。不过，在本文的其余部分，我们将假设特征之间存在一些关联，并且大多数异常值都是不寻常的值组合。

处理掺杂数据

大多数离群值检测器（少数例外）都有独立的训练和预测步骤。因此，大多数异常值检测器都类似于预测模型。在训练步骤中，要对训练数据进行评估，并找出数据中的正常模式（例如，记录之间的正常距离、频繁项目集、聚类、特征之间的线性关系等）。然后，在预测步骤中，将测试数据集（可能是用于训练的相同数据，也可能是单独的数据）与训练期间发现的模式进行比较，并为每一行分配离群值（或在某些情况下，二进制标签）。

有鉴于此，我们有两种主要方法来处理掺杂数据：

1. 在训练数据中加入兴奋剂记录

我们可能会在训练数据中加入少量使用兴奋剂的记录，然后将这些数据也用于测试。这可以测试我们检测当前可用数据中异常值的能力。这是离群值检测中的一项常见任务：在给定一组数据的情况下，我们通常希望找到该数据集中的离群值（当然也可能希望找到后续数据中的离群值--相对于该训练数据的标准异常的记录）。

这样做时，我们可以只使用少量掺杂记录进行测试，因为我们不希望对数据的整体分布产生重大影响。然后我们检查是否能将这些记录识别为异常值。其中一个关键测试是在训练数据中同时包含原始和掺杂记录，以确定检测器对掺杂记录的评分是否明显高于同一记录的原始版本。

不过，我们也希望检查掺杂记录的得分是否普遍最高（当然，有些未经修改的原始记录可能比掺杂记录更异常，而有些掺杂记录可能并不异常）。

鉴于我们只能使用少量掺杂记录进行测试，这一过程可能会重复多次。

不过，掺杂数据仅用于以这种方式评估探测器。在创建用于生产的最终模型时，我们将只对原始（真实）数据进行训练。

如果我们能够可靠地检测出数据中的掺杂记录，我们就有理由相信，我们能够识别出同一数据中的其他异常值，至少是与掺杂记录相似的异常值（但不一定是更微妙的异常值--因此，我们希望包含有相当微妙的掺杂记录的测试）。

2. 仅在测试数据中包含掺杂记录

也可以只使用真实数据（我们可以假定这些数据基本上没有异常值）进行训练，然后使用真实数据和掺杂数据进行测试。这样，我们就可以在相对干净的数据上进行训练（真实数据中的某些记录会是异常值，但大多数记录都是典型的，而且不会受到掺杂记录的污染）。

这也让我们可以使用实际的离群值检测器进行测试，这些检测器有可能会投入生产（这取决于它们在掺杂数据下的表现--与我们测试的其他检测器相比，以及与我们对检测器最低应有表现的认识相比）。

这将测试我们在未来数据中检测异常值的能力。这也是离群值检测的另一种常见情况：我们有一个数据集，可以假定这个数据集是比较干净的（要么没有离群值，要么只包含一小部分典型的离群值，没有任何极端离群值），我们希望将未来的数据与这个数据集进行比较。

只使用真实数据进行训练，同时使用真实数据和掺杂数据进行测试，我们可以使用任意数量的掺杂数据进行测试，因为掺杂数据只用于测试而不用于训练。这样，我们就可以创建一个大型测试数据集，从而获得更可靠的测试数据。

创建掺杂数据的算法

创建掺杂数据的方法有很多，其中包括《Python 中的离群点检测》一书中介绍的几种方法，每种方法都有自己的优缺点。为简单起见，本文只介绍一种方法，即以相当随机的方式修改数据：随机选择被修改的单元格，并随机创建替代原始值的新值。

在这种情况下，一些掺杂的记录有可能并不真正异常，但在大多数情况下，随机赋值会破坏特征之间的一个或多个关联。我们可以假定掺杂记录基本上是异常的，但也有可能只是轻微异常，这取决于它们是如何创建的。

示例

下面我们以一个真实数据集为例，对其进行修改，并测试修改后的数据集的检测效果。

在这个例子中，我们使用的是 OpenML 上的一个数据集，名为 abalone。

虽然还可以进行其他预处理，但在本例中，我们对分类特征进行了一次性编码，并使用 RobustScaler 对数字特征进行了缩放。

我们使用三种离群值检测器进行测试，分别是 Isolation Forest、LOF 和 ECOD，它们都可以在流行的 PyOD 库中找到（必须安装 pip 才能执行）。

在进行任何训练或测试之前，我们还使用 Isolation Forest 清理数据（移除任何强离群值）。这一步并非必要，但在离群点检测中通常很有用。

这是上述两种方法中第二种方法的示例，我们使用原始数据进行训练，并同时使用原始数据和掺杂数据进行测试。

import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.preprocessing import RobustScaler
import matplotlib.pyplot as plt
import seaborn as sns
from pyod.models.iforest import IForest
from pyod.models.lof import LOF
from pyod.models.ecod import ECOD
# Collect the data
data = fetch_openml('abalone', version=1) 
df = pd.DataFrame(data.data, columns=data.feature_names)
df = pd.get_dummies(df)
df = pd.DataFrame(RobustScaler().fit_transform(df), columns=df.columns)
# Use an Isolation Forest to clean the data
clf = IForest() 
clf.fit(df)
if_scores = clf.decision_scores_
top_if_scores = np.argsort(if_scores)[::-1][:10]
clean_df = df.loc[[x for x in df.index if x not in top_if_scores]].copy()
# Create a set of doped records
doped_df = df.copy() 
for i in doped_df.index:
  col_name = np.random.choice(df.columns)
  med_val = clean_df[col_name].median()
  if doped_df.loc[i, col_name] > med_val:
    doped_df.loc[i, col_name] = \   
      clean_df[col_name].quantile(np.random.random()/2)
  else:
    doped_df.loc[i, col_name] = \
       clean_df[col_name].quantile(0.5 + np.random.random()/2)
# Define a method to test a specified detector. 
def test_detector(clf, title, df, clean_df, doped_df, ax): 
  clf.fit(clean_df)
  df = df.copy()
  doped_df = doped_df.copy()
  df['Scores'] = clf.decision_function(df)
  df['Source'] = 'Real'
  doped_df['Scores'] = clf.decision_function(doped_df)
  doped_df['Source'] = 'Doped'
  test_df = pd.concat([df, doped_df])
  sns.boxplot(data=test_df, orient='h', x='Scores', y='Source', ax=ax)
  ax.set_title(title)
# Plot each detector in terms of how well they score doped records 
# higher than the original records
fig, ax = plt.subplots(nrows=1, ncols=3, sharey=True, figsize=(10, 3)) 
test_detector(IForest(), "IForest", df, clean_df, doped_df, ax[0])
test_detector(LOF(), "LOF", df, clean_df, doped_df, ax[1])
test_detector(ECOD(), "ECOD", df, clean_df, doped_df, ax[2])
plt.tight_layout()
plt.show()

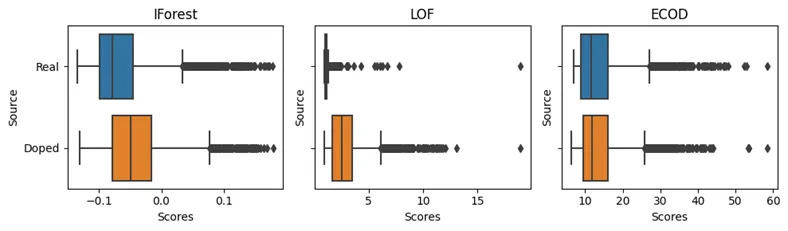
在这里，为了创建掺杂记录，我们复制了全套原始记录，因此掺杂记录的数量与原始记录的数量相等。对于每条掺杂记录，我们随机选择一个特征进行修改。如果原始值低于中位数，我们就创建一个高于中位数的随机值；如果原始值低于中位数，我们就创建一个高于中位数的随机值。

在这个例子中，我们可以看到 IF 对掺杂记录的评分确实较高，但并不明显。至少对于这种形式的掺杂，LOF 能很好地区分掺杂记录。ECOD 是一种只检测异常小或异常大的单个值，而不检测异常组合的检测器。由于本例中使用的掺杂不会产生极端值，只会产生不寻常的组合，因此 ECOD 无法区分掺杂记录和原始记录。

本例使用方框图来比较检测器，但通常我们会使用一个客观的分数，通常是 AUROC（接收器运算曲线下面积）分数来评估每个检测器。我们通常还会测试模型类型、预处理和参数的多种组合。

其他掺杂方法

上述方法往往会产生违反特征间正常关联的掺杂记录，但也可以使用其他掺杂技术来降低这种可能性。例如，在考虑第一分类列时，我们可以选择一个新值，同时满足以下两个条件：

1. 新值与原始值不同
2. 新值与该行中其他值的预测值不同。为此，我们可以创建一个预测模型来预测这一列的当前值，例如随机森林分类器。

对于数值数据，我们可以通过将每个数值特征分为四个四分位数（或某个数量的四分位数，但至少要有三个）来实现等效的预测。对于数值特征中的每一个新值，我们都要选择一个值，以便同时满足以下两个条件：

1. 新值处于与原值不同的四分位数中
2. 新值所处的四分位数与该行其他值的预测值不同。

例如，如果原始值位于 Q1，而预测值位于 Q2，那么我们可以在 Q3 或 Q4 中随机选择一个值。这样，新值就很可能违背特征之间的正常关系。

创建一套测试数据集

目前还没有确切的说法来说明一个记录被掺杂后的异常程度。不过，我们可以假设，平均而言，修改的特征越多，修改的次数越多，掺杂的记录就越异常。我们可以利用这一点来创建多个测试套件，而不是一个测试套件，这样就能更准确地评估离群点检测器。

例如，我们可以创建一组非常明显的掺杂记录（每条记录中都有多个特征被修改，每个特征的值都与原始值有显著差异），一组非常细微的掺杂记录（只有一个特征被修改，与原始值没有显著差异），以及许多介于两者之间的难度级别。这有助于很好地区分探测器。

因此，我们可以创建一套测试集，根据被修改特征的数量和被修改的程度，为每个测试集设定一个（大致估算的）难度级别。考虑到某些特征中的异常值可能更相关，或者更容易或更难检测，我们还可以使用不同的测试集来修改不同的特征。

不过，重要的是，任何掺杂行为都代表了异常值的类型，如果它们确实出现在真实数据中，就会引起人们的兴趣。理想情况下，掺杂的记录集还能很好地涵盖你有兴趣检测的范围。

如果满足了这些条件，并创建了多个测试集，这对于选择性能最佳的检测器和估计它们在未来数据上的性能是非常有用的。我们无法预测有多少异常值会被检测到，也无法预测你将看到的假阳性和假阴性的程度--这些在很大程度上取决于你将遇到的数据，而在异常值检测中，这是很难预测的。但是，我们可以对可能检测到或检测不到的异常值类型有一个大致的了解。

可能更重要的是，我们还能很好地创建有效的离群值检测器集合。在离群值检测中，大多数项目通常都需要集合。由于某些检测器会捕捉到某些类型的异常值，而漏掉其他类型的异常值，而其他检测器会捕捉到其他类型的异常值，但也会漏掉其他类型的异常值，因此我们通常只能使用多个检测器来可靠地捕捉我们感兴趣的异常值范围。

创建集合本身就是一个庞大而复杂的领域，与预测模型的集合也有所不同。不过，就本文而言，我们可以指出，了解每个检测器能检测哪些类型的异常值，就能让我们知道哪些检测器是多余的，哪些检测器能检测大多数其他检测器无法检测的异常值。

结论

很难评估任何特定的离群值检测器对当前数据中离群值的检测效果如何，更难评估它对未来（未见的）数据的检测效果如何。如果有两个或更多的离群值检测器，也很难评估哪一个在当前和未来的数据中表现更好。