人工智能数学奥林匹克（AIMO）是评估人工智能模型复杂数学推理能力的最有趣的活动之一。AIMO 于几个月前启动，为那些推理能力达到国际高中生数学奥林匹克（IMO）竞赛金牌得主水平的模型设立了 1000 万美元的奖金。要达到这些水平，人工智能模型需要在多步骤推理、数学以及深层次语言理解等领域展现出复杂的能力。

Numina 是一家致力于提高基础模型数学能力的实验室。你可能对 HuggingFace 有很多了解，但对 Numina 却知之甚少，因此让我们来了解一下。

Numina 是一个致力于提高基础模型数学能力的实验室。Numina 的愿景是 “数学对人类至关重要，是智能进步的关键组成部分”。该项目最初得到了 Mistral 和 General Catalyst 等公司的支持，并将 AIMO 挑战赛作为首批主要测试项目之一。

NuminaMath 结合了一些显而易见的步骤和跨领域的新颖方法。今天，我想深入探讨一下 NuminaMath 背后的一些细节，希望能对研究类似问题的人工智能团队有所启发。

NuminaMath

NuminaMath 最有趣的一点是，他们从零开始构建了一个全新的架构。相反，他们以 DeepSeekMath 模型为基准，并在此基础上扩展了一种基于三个基本组件的新方法：

1. 微调策略： NuminaMath 对 DeepSeekMath-Base 7B 模型进行微调，使其发挥 “推理代理 ”的功能。该代理使用自然语言推理结合 Python REPL 来计算中间结果，从而解决数学问题。
2. 解码算法： 他们为工具集成推理（TIR）开发了一种新颖的解码算法，该算法结合了代码执行反馈，能够在推理过程中生成候选解决方案。
   
3. 内部验证集： 使用各种内部验证集来指导模型选择，并防止过度拟合公共排行榜。
   

模型使用 TRL、PyTorch、vLLM 和 DeepSpeed 等开源库进行训练。在由 8 x H100 GPU 组成的一个节点上进行训练大约需要 10 个小时。

训练配方

可以说，微调是 NuminaMath 最有趣的贡献领域之一。

微调过程分为两个阶段：

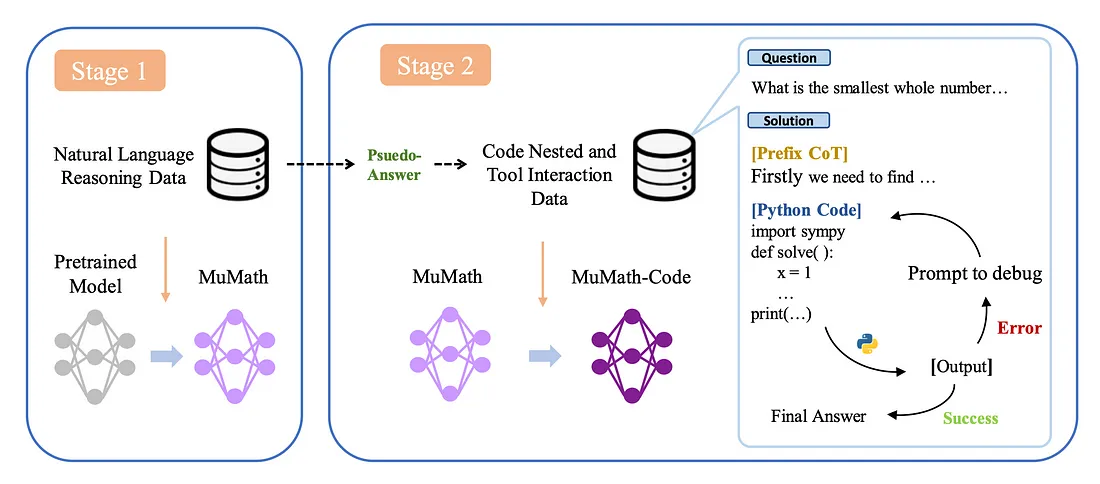
第 1 阶段：在自然语言数学问题和解决方案的各种数据集上对基础模型进行微调。每个解决方案都以思维链（CoT）为模板，以帮助推理。

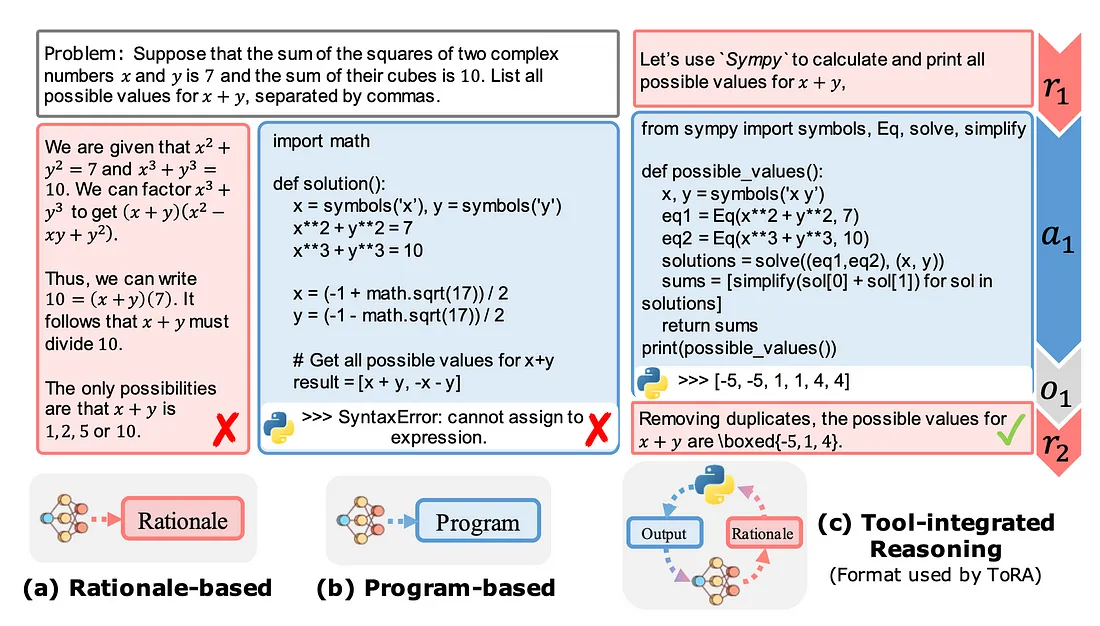
第 2 阶段：在工具集成推理的合成数据集上进一步微调第 1 阶段的模型。问题被分解为推理、Python 程序及其输出。这种方法受到微软 ToRA 论文的影响，产生了一个能够使用自然语言和 Python REPL 解决问题的推理代理。

这两个阶段都涉及 “全面微调”，即在反向传播过程中更新所有模型权重。TRL 的 SFTTrainer 具有 “打包 ”功能，可将多个样本串联成一个包含 2048 个标记的单块。梯度检查点和 DeepSpeed ZeRO-3 协议确保了在可用 VRAM 内进行高效训练。每个阶段使用的关键超参数包括 2.0 E-5 的学习率、32 个批次的总规模以及余弦学习率调度器。

初步尝试和调整

仅使用第一阶段微调的初始提交取得了有限的成功。受 Abdur Rafae 公开获奖笔记本的启发，NuminaMath 将代码执行整合到了他们的训练配方中。他们首先探索了混合最优集（MMOS）数据集，但发现该数据集不足以解决更难的问题。这促使他们开发了一个类似于 DeepSeekMath Instruct / RL 模型所使用的数据集，从而取得了显著的改进。

数据集构建

NuminaMath 在微调过程中使用了两个主要数据集：

1. 思维链数据集： 由几十万个问题组成，这些问题的解决方案是以 “思维链 ”的方式编写的。数据来源包括中国高中数学练习题和国际数学竞赛题。这些数据经过 OCR、分割、翻译成英语和重新调整，以生成思维链格式。
2. 工具集成推理数据集： 重点研究了来自 Numina 数据集中的 60,000 个有数字输出的问题。他们使用 GPT-4 的流水线，生成类似 TORA 的推理路径，并执行代码来产生结果。对解决方案进行反复过滤和改进，以确保准确性。

SC-TIR 算法

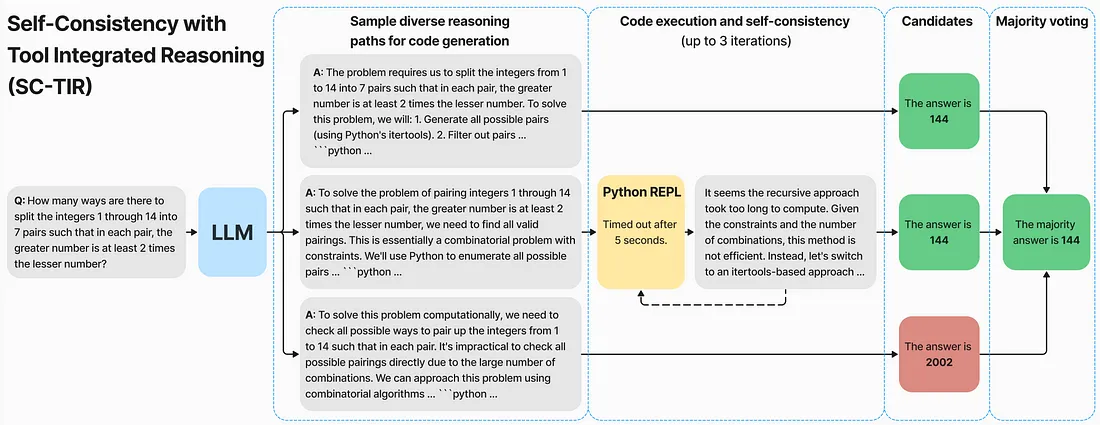
为解决模型评估中的高差异问题，NuminaMath 开发了 SC-TIR 算法。这包括：

• 复制输入 N 次，以定义初始提示批次。
• 对 N 次不同的完成情况进行采样，直到生成一个完整的 Python 代码块。
  
• 执行每个 Python 代码块并连接输出。
  
• 重复该过程 M 次，以便自我纠正代码错误。
  
• 后处理并应用多数投票选出最终答案。
  

在获胜的提交中，他们生成了 N=48 个深度为 M=4 的候选答案。将模型量化到 8 位精度提高了上传速度，并在不明显影响精度的情况下适应了 GPU 限制。

避免过度拟合：

为减少对公开排行榜的过度拟合，NuminaMath 使用了四个内部验证集，涵盖不同难度的问题。其中包括 AMC12（2022 年、2023 年）和 AIME（2022 年、2023 年、2024 年）的数据集，以及 MATH 测试集的子集。这种方法使他们能够选择最有前途的模型，并有效地微调超参数，在小型代表集与大型代表集之间取得平衡，以管理提交的随机性。

失败之处和有前途的想法

NuminaMath 并非事事成功。团队尝试了不同的想法，例如：

1. 带多数投票的 CoT 模型： 他们训练了一个纯粹的思维链（CoT）模型，并使用多数投票法对其进行评估。这种方法没有取得预期的结果。

2. 单步求解的 MMOS 模型： 他们还尝试训练一个基于最小最优集混合（MMOS）的模型，以使用单步 Python 解决问题。这种方法也没有成功。

有前途的方法： 卡KTO

另一种技术是将 KTO 应用于从 SFT 模型中采样的新完井。这种方法受到 OrcaMath 的启发，包括以下步骤：

1. 从 SFT 模型中抽取每个问题的四个完成答案，使用结合了第二阶段数据集的理由和代码执行的提示。
2. 将提取的答案与基本事实进行比较，如果正确则标记为正样本，如果错误则标记为负样本。

虽然这种形式的政策性 KTO 生成的模型比 SFT 模型略好，但在内部评估中只取得了微弱的改进（几个百分点），在公共排行榜上的得分为 27/50。使用 KTO 的一个优势是可以在训练过程中跟踪隐式奖励，这对调试有很大帮助。例如，成功的训练日志显示，正确解决方案的奖励增加，而错误解决方案的奖励减少。

遗憾的是，该团队没有足够的时间将 KTO 纳入 NuminaMath，但这一想法似乎很有前途。

结果

NuminaMath 回答了 50 个问题中的 29 个，登上了 AIMO 排行榜的榜首。值得注意的是，该模型比第二名多回答了 7 个模型。

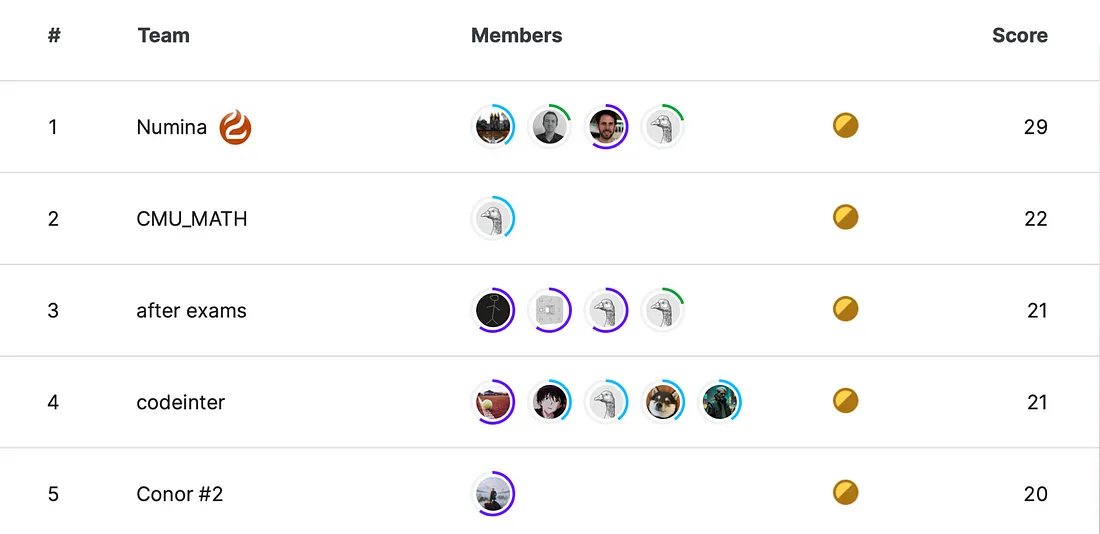
NuminaMath 代表了数学推理前沿模型的一次重要迭代。AIMO 奖可能是我们能找到的数学推理方面最高级别的测试之一，而 NuminaMath 的表现令人印象深刻。希望 NuminaMath 背后的一些想法能够启发数学推理领域的其他模型。