时间序列预测在金融、制造、卫生、气象研究和社会科学等领域发挥着非常重要的作用。这些领域依靠这些预测来猜测未来的需求和销售数字。这有助于他们微调库存，提高供应链的效率。这使他们能够在金融、营销和风险相关领域做出明智的选择。因此，精确预测是企业适应市场变化和领先竞争对手的必要条件。

人们通常会选择 ARIMA（自回归整合移动平均）、指数平滑和时间序列季节分解 (STL) 等标准模型来进行时间序列分析。这些模型之所以好，是因为它们易于理解，与数据假设相匹配，并以坚实的理论为基础。这也是它们成为未来预测首选的原因。

随着机器学习的发展，我们发现它们在时间序列数据预测中的应用大幅增加。bagging和boosting等工具之所以能脱颖而出，是因为它们能在时间序列数据中发现棘手的模式和不寻常的联系。它们的独特之处在于直接从原始数据中学习。它们可以处理海量数据并做出准确的猜测。

下面是一个实际用例，同时使用统计预测和基于机器学习的预测来预测未来。研究接着根据某些准确度指标对预测进行比较，以判断机器学习模型是否能与传统模型竞争。

预测工具包

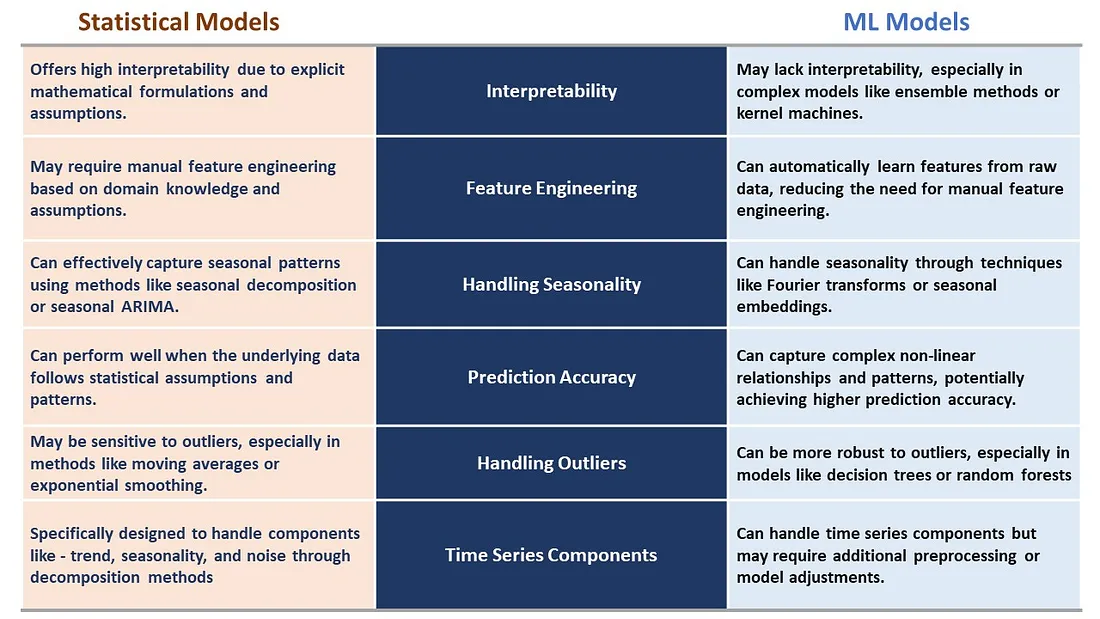
像 ARIMA 和 ETS 这样的统计预测算法一直是时间序列预测领域的佼佼者。pmdarima 和 statsforecast 等库在各种实际和工业用例中表现出色。然而，新的、先进的机器学习模型由于能够从原始数据中学习复杂的模式而占据了主导地位。让我们简要观察一下这些算法之间的差异。

让我们集合起来

我们将在本研究中探讨的机器学习模型是基于集合原理的。集合模型是一种在预测过程中将多个其他模型结合起来的机器学习方法。这些模型被称为基础估计器。因此，集合模型使用模型集合来代替单个模型进行预测。

Ensemble 使用两种方法：

Bagging： 它从样本训练数据中创建不同的训练子集，并进行替换，最终输出基于多数投票，如随机森林。

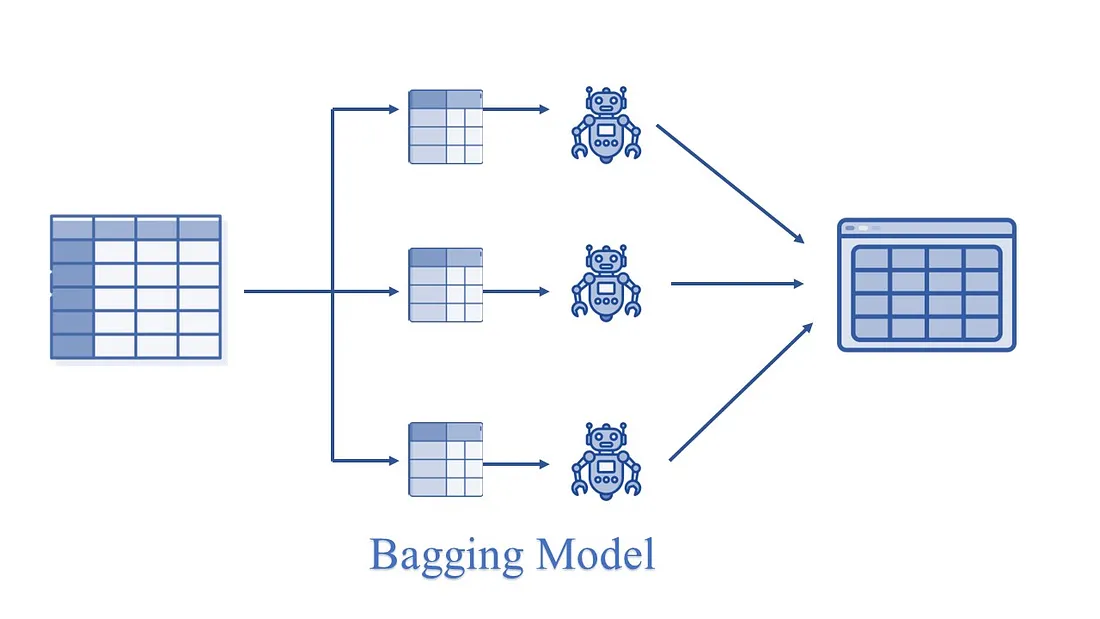
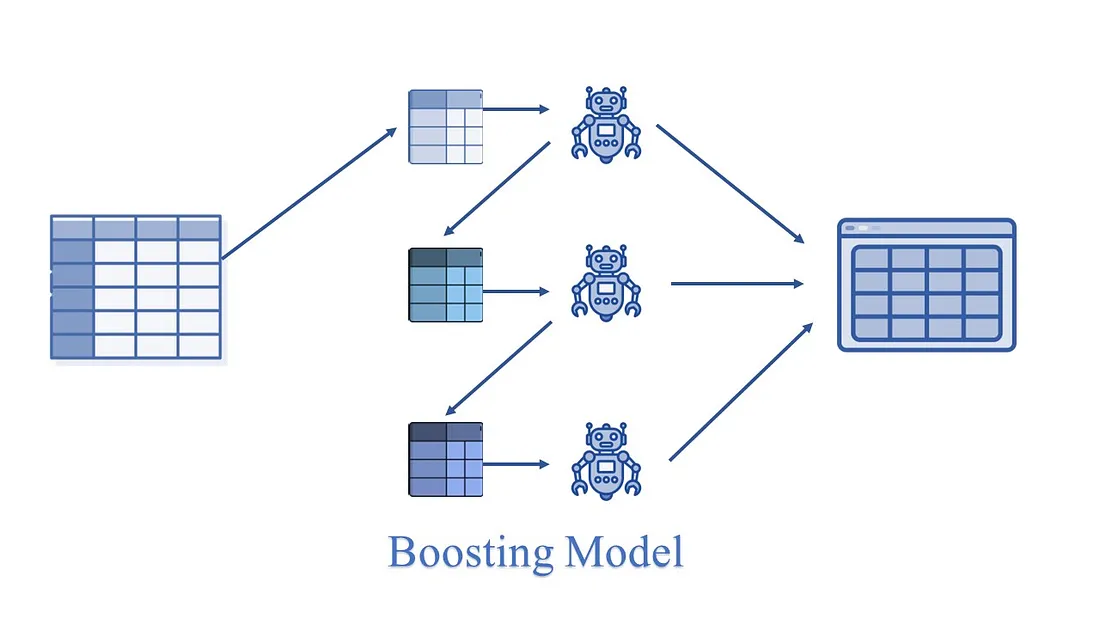
Boosting： 它通过创建一个连续的模型，将弱学习者合并为强学习者，从而使最终模型具有最高的准确率。

例如，LGBM、XGB 等。

数据分析

现在让我们进入实验部分：

让我们先安装库。

#Install statsforecast
!pip install statsforecast
#Install mlforecast. 
#This will also install collected packages: window-ops, utilsforecast, mlforecast
!pip install mlforecast
#Install pmdarima
!pip install pmdarima

本研究中使用的 StatsForecast 和 MLForecast 软件包由 NIXTLA 团队设计。

现在让我们导入本研究需要的库。

import os
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.stattools import adfuller
from statsforecast import StatsForecast
from pmdarima import auto_arima
from statsforecast.models import AutoARIMA
from statsmodels.tsa.holtwinters import ExponentialSmoothing
from mlforecast import MLForecast
from mlforecast.target_transforms import Differences
from numba import njit
from window_ops.expanding import expanding_mean
from window_ops.rolling import rolling_mean
import lightgbm as lgb
import xgboost as xgb
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor

让我们读取数据并将其可视化。

file_path = "AirPassengers.csv"
df = pd.read_csv(file_path)
df['Month'] = pd.to_datetime(df['Month'])
df = df.set_index('Month').resample('MS').mean()
df = df.interpolate() #to interpolate and fill missing values
df.reset_index(inplace=True)
print(df.head())

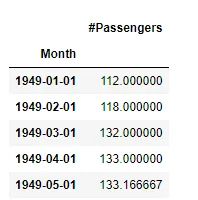
让我们将数据集可视化。

sns.set(style="darkgrid")
plt.figure(figsize=(10, 6))
sns.lineplot(x="Month", y='#Passengers', data=df, color='#ff9f9b')
plt.title('Monthly Sales Over Time')
plt.xlabel('Month')
plt.ylabel('#Passengers')
plt.show()

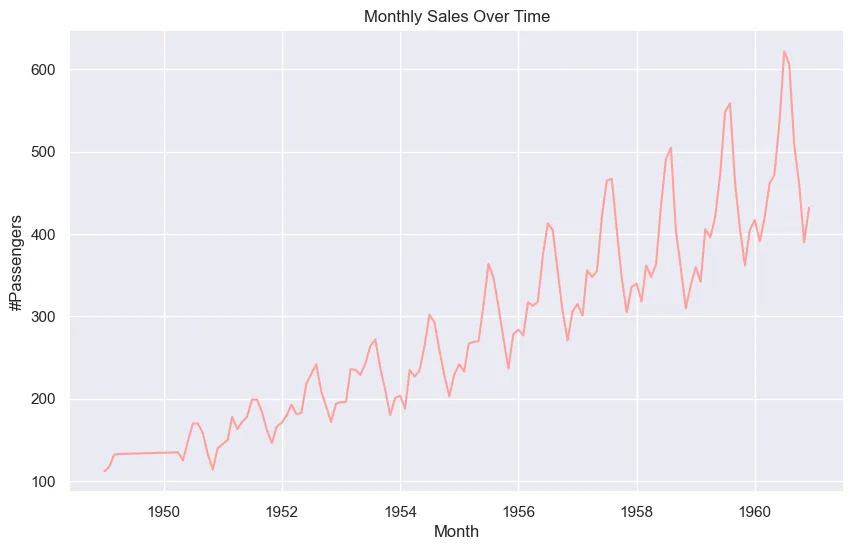
现在，让我们对这些数据进行季节性分解。

result = seasonal_decompose(df['#Passengers'], model='additive')
fig, (ax1, ax2, ax3, ax4) = plt.subplots(4, 1, figsize=(10, 12))
result.observed.plot(ax=ax1, color="blue")
ax1.set_ylabel('Observed')
result.trend.plot(ax=ax2, color='blue')
ax2.set_ylabel('Trend')
result.seasonal.plot(ax=ax3, color='blue')
ax3.set_ylabel('Seasonal')
result.resid.plot(ax=ax4, color='blue')
ax4.set_ylabel('Residual')
plt.tight_layout()
plt.show()

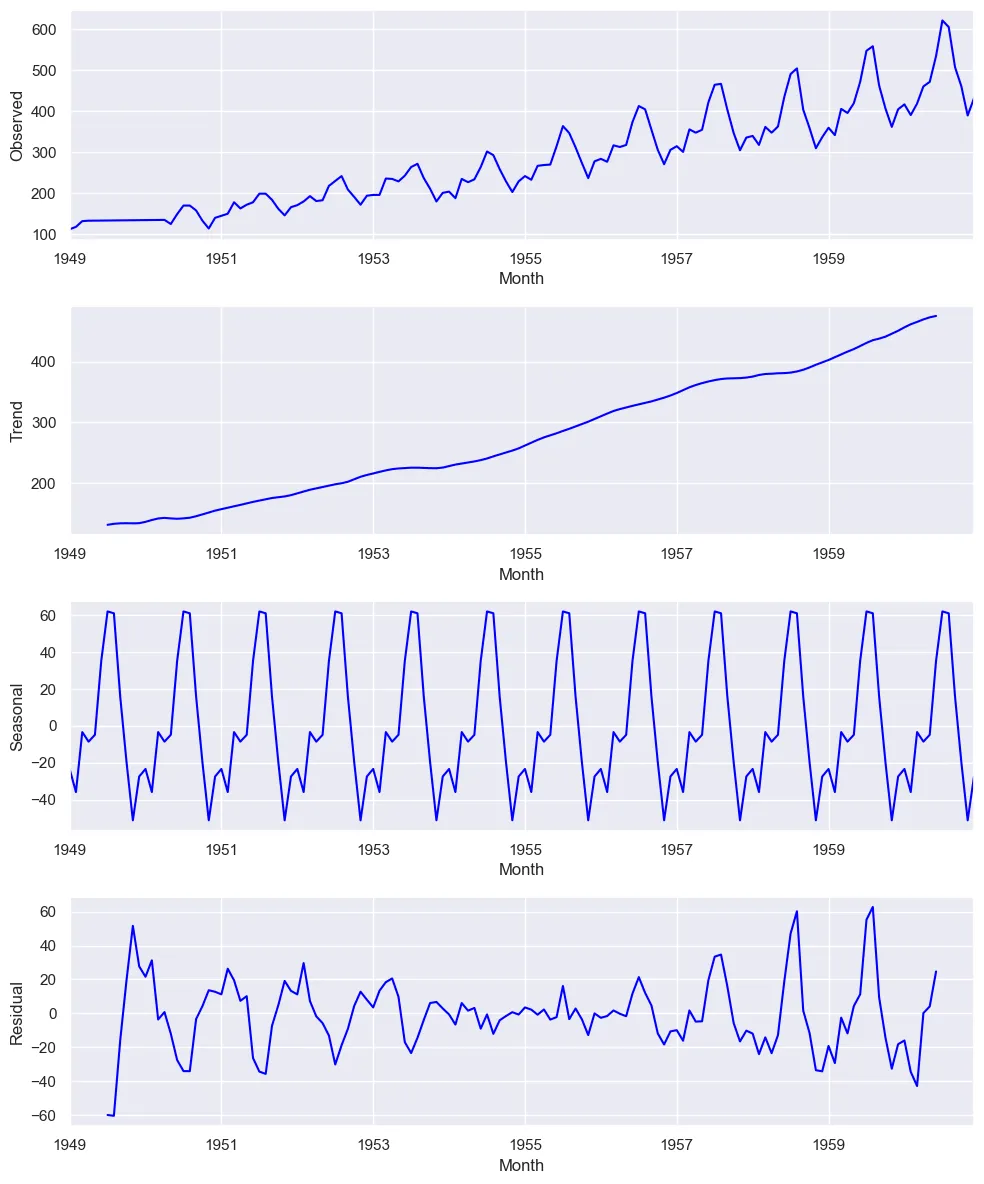
建立模型

现在我们来构建统计和机器学习模型。

#Train-Test Split
train_size = int(len(df) * 0.8)
train, test = df.iloc[:train_size], df.iloc[train_size:]
print(f'Train set size: {len(train)}')
print(f'Test set size: {len(test)}')

使用 pmdarima 进行预测

pmdarima_model = auto_arima(train['#Passengers'], seasonal=True, m=12)
pmdarima_forecast = pmdarima_model.predict(n_periods=len(test))
pmdarima_forecast_df = pd.DataFrame({'Date': test["Month"],
                        'PMDARIMA_Forecast': pmdarima_forecast})

使用指数平滑法进行预测

ets_model = ExponentialSmoothing(train['#Passengers'], 
            seasonal='mul', seasonal_periods=12).fit()
ets_forecast = ets_model.forecast(steps=len(test))
ets_forecast_df = pd.DataFrame({'Date': test["Month"],
                                'ETS_Forecast': ets_forecast})

使用 StatsForecast 库进行预测

train_ = pd.DataFrame({'unique_id':[1]*len(train),
        'ds': train["Month"], "y":train['#Passengers']})
test_ = pd.DataFrame({'unique_id':[1]*len(test),
        'ds': test["Month"], "y":test['#Passengers']})
sf_forecast = StatsForecast(models = [AutoARIMA(season_length = 12)],freq = 'MS')
sf_forecast.fit(train_)
sf_prediction = sf_forecast.predict(h=len(test))
sf_prediction.rename(columns={'ds': 'Month'}, inplace=True)

使用 MLForecast 库进行预测 - 线性回归、随机森林回归、轻型 GBM 回归和极端梯度提升回归。

models = [LinearRegression(),
    lgb.LGBMRegressor(verbosity=-1),
    xgb.XGBRegressor(),
    RandomForestRegressor(random_state=0),
]
@njit
def rolling_mean_3(x):
    return rolling_mean(x, window_size=3)
@njit
def rolling_mean_6(x):
    return rolling_mean(x, window_size=6)
fcst = MLForecast(
    models=models,
    freq='MS',
    lags=[1,3,5,7,12],
    lag_transforms={
        1: [expanding_mean],
        3: [rolling_mean_3, rolling_mean_6],
        5: [rolling_mean_3, rolling_mean_6],
        7: [rolling_mean_3, rolling_mean_6],
        12: [rolling_mean_3, rolling_mean_6],
    },
    date_features=['year', 'month', 'day', 'quarter'],
    target_transforms=[Differences([1])])
fcst.fit(train_)
ml_prediction = fcst.predict(len(test_))
ml_prediction.rename(columns={'ds': 'Month'}, inplace=True)

性能评估和比较

现在，让我们将预测合并到一个数据帧中，并根据准确度度量对它们进行比较。

fcst_result = test.copy()
fcst_result.set_index("Month", inplace=True)
fcst_result["AutoARIMA_fcst"]=sf_prediction["AutoARIMA"].values
fcst_result["PMDArima_fcst"]=pmdarima_forecast_df["PMDARIMA_Forecast"].values
fcst_result["ETS_fcst"]=ets_forecast_df["ETS_Forecast"].values
fcst_result["LinearRegression_fcst"]=ml_prediction["LinearRegression"].values
fcst_result["LGBM_fcst"]=ml_prediction["LGBMRegressor"].values
fcst_result["XGB_fcst"]=ml_prediction["XGBRegressor"].values
fcst_result["RandomForest_fcst"]=ml_prediction["RandomForestRegressor"].values
print(fcst_result.head())

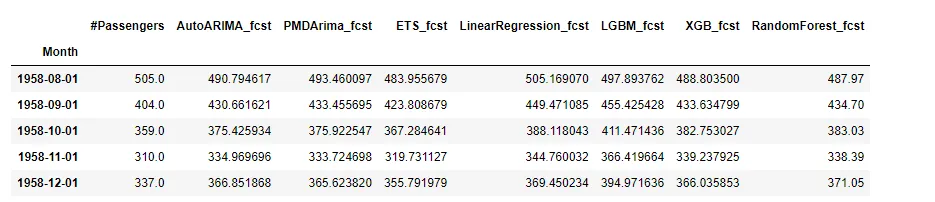
现在，让我们来计算准确度指标，以比较这些预测算法的性能。

#Defining a function to calculate the error metrices
def calculate_error_metrics(actual_values, predicted_values):
    actual_values = np.array(actual_values)
    predicted_values = np.array(predicted_values)
    metrics_dict = {
        'MAE': np.mean(np.abs(actual_values - predicted_values)),
        'RMSE': np.sqrt(np.mean((actual_values - predicted_values)**2)),
        'MAPE': np.mean(np.abs((actual_values - predicted_values) / actual_values)) * 100,
        'SMAPE': 100 * np.mean(2 * np.abs(predicted_values - actual_values) / (np.abs(predicted_values) + np.abs(actual_values))),
        'MdAPE': np.median(np.abs((actual_values - predicted_values) / actual_values)) * 100,
        'GMRAE': np.exp(np.mean(np.log(np.abs(actual_values - predicted_values) / actual_values)))
    }
    result_df = pd.DataFrame(list(metrics_dict.items()), columns=['Metric', 'Value'])
    return result_df

actuals = fcst_result['#Passengers']

error_metrics_dict = {}

for col in fcst_result.columns[1:]: 
    predicted_values = fcst_result[col]
    error_metrics_dict[col] = calculate_error_metrics(actuals, predicted_values)['Value'].values  # Extracting 'Value' column

error_metrics_df = pd.DataFrame(error_metrics_dict).T.reset_index()
error_metrics_df.columns = ['Model', 'MAE', 'RMSE', 'MAPE', 'SMAPE', 'MdAPE', 'GMRAE']
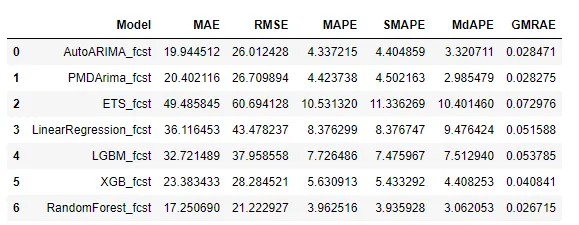
error_metrics_df

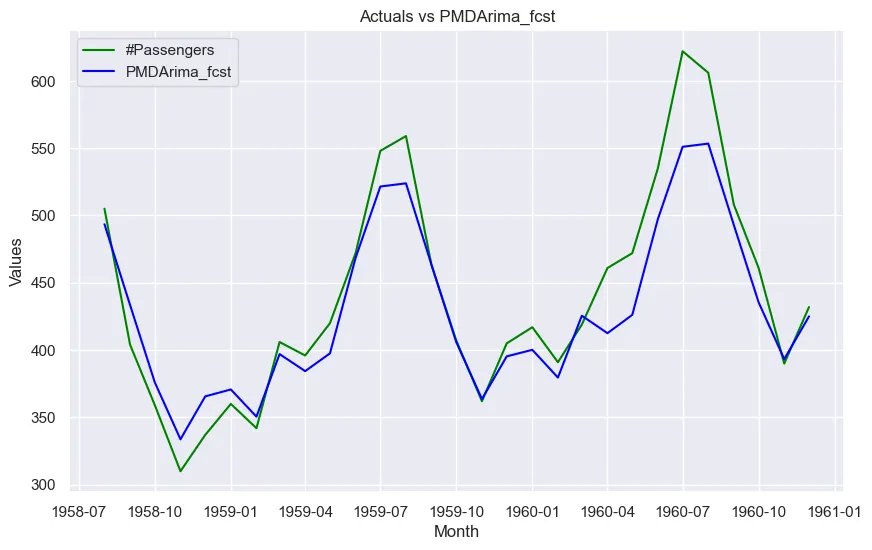
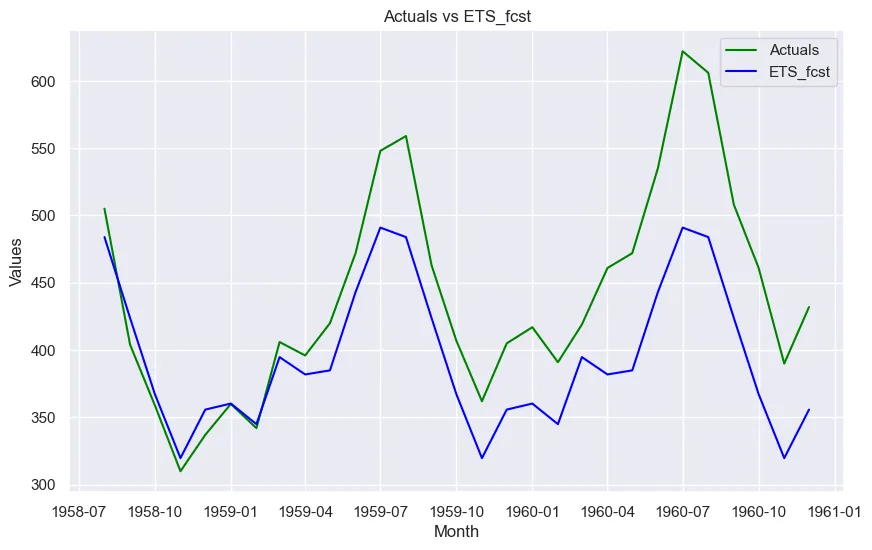
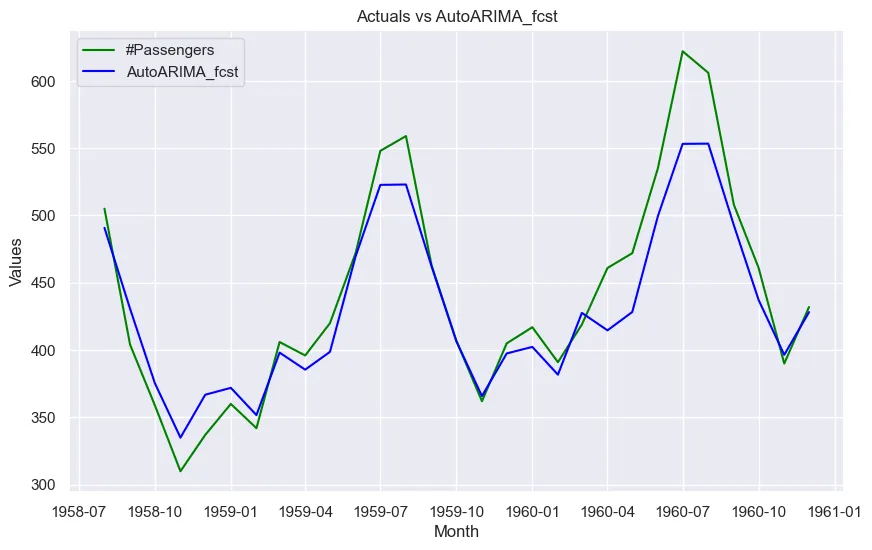
让我们将实际数据与每项预测进行对比。

sns.set(style="darkgrid")
for col in fcst_result.columns[1:]:
    plt.figure(figsize=(10, 6))   
    plt.plot(fcst_result.index, fcst_result['#Passengers'], label='Actuals', color='green')
    plt.plot(fcst_result.index, fcst_result[col], label=col, color='blue')
    plt.title(f'Actuals vs {col}')
    plt.xlabel('Month')
    plt.ylabel('Values')
    plt.legend()
    plt.show()

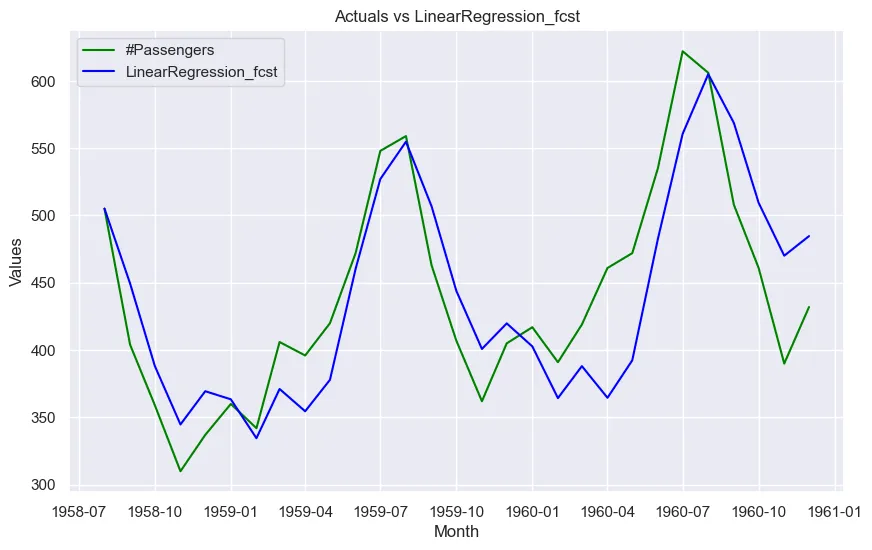
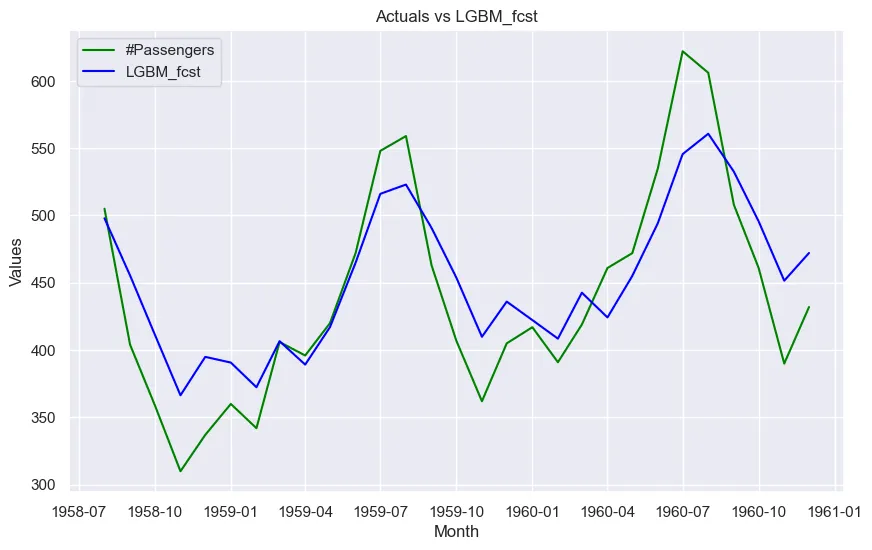
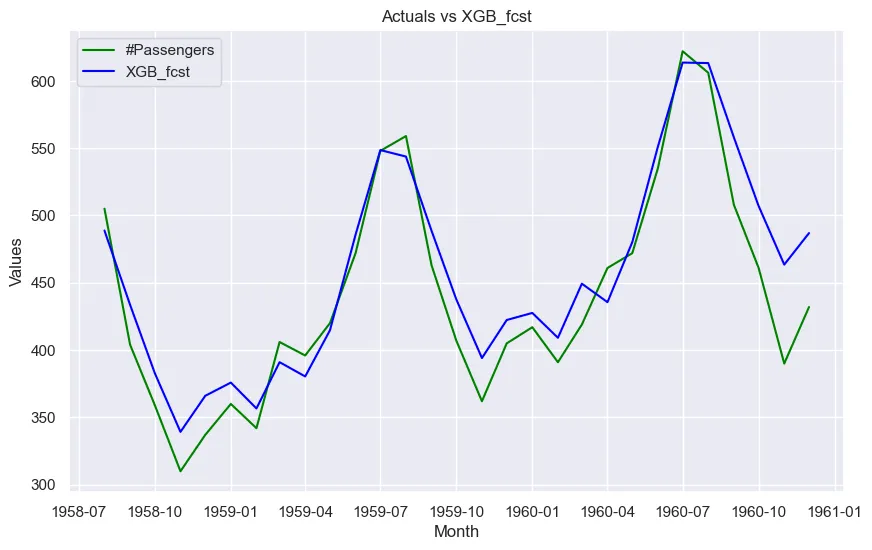
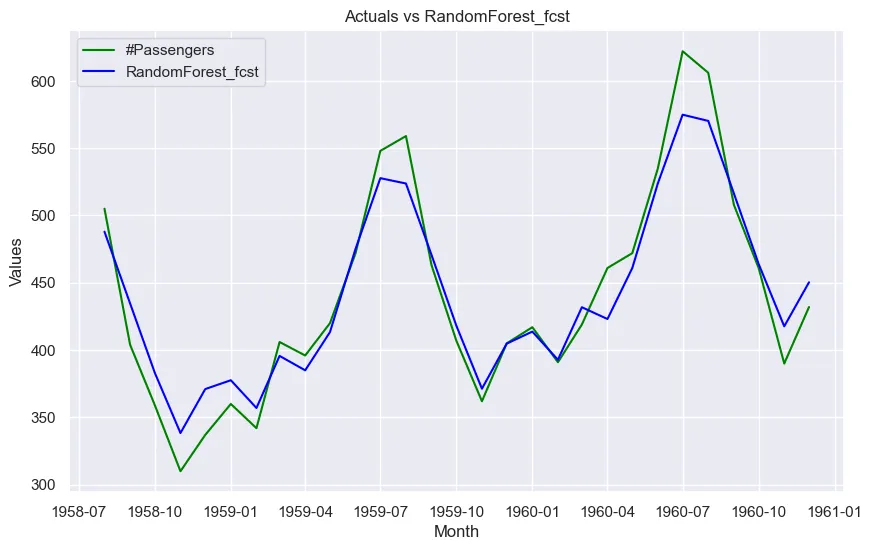
从该数据集的误差指标可以看出：

1. 随机预测回归给出了所有指标的最低值，包括 RMSE 和 MAPE。它优于传统的统计模型，这是本研究的一个有趣发现。
2. 在 MAPE、RMSE 和 MAE 方面，提升算法（Light GBM 和 XGBoost 回归）的性能也优于指数平滑等统计模型。
3. XGB 和 LGBM 等 ML 预测模型的性能也令人满意，因为它们的准确度指标与统计模型一致。

总结

在时间序列预测方面，机器学习模型能否优于统计模型是一个一直争论不休的话题。这两种方法各有优缺点。模型的性能取决于各种因素，如数据的特征（季节性、趋势和残差）、具体的预测任务、模型超参数、计算资源、可解释性要求以及简单性和准确性之间的权衡。

众所周知，统计模型能有效捕捉时间序列数据中的线性趋势、季节性模式和自相关性。此外，机器学习模型也很受欢迎，因为它们能够捕捉数据中复杂的非线性关系和模式。

这项研究充分证明，机器学习模型在与既有统计模型的竞争中占有优势。随机森林、XGB 和 LGBM 等模型都给出了相当令人满意的预测结果，随机森林在这一流行的基准数据集上的表现也优于 AutoARIMA 和 ETS。