简介

想象一下，如果你能像语言模型理解文本一样轻松地预测未来趋势，那该有多好。无论是预测股票价格、医疗保健需求还是优化物流，准确的时间序列预测都至关重要。ARIMA 等传统方法难以应对现代数据的复杂性，但深度学习已显示出其前景。

现在，想象一下一个专为时间序列数据定制的大型预训练模型--一个无需大量再训练就能提供准确预测的模型。这就是Abhimanyu Das、Weihao Kong、Rajat Sen 和 Yichen Zhou 的开创性工作。他们的纯解码器模型受到 BERT 等 NLP 巨头的启发，采用基于补丁的方法高效处理数据。该模型在不同的数据集上进行了训练，在零样本场景下提供了接近监督的性能。

在本文中，我们将讨论该模型的架构、模型的训练，并进行一个实际预测案例研究，在该案例研究中，我们将对 TimesFM 的预测能力进行分析，并将该模型与统计和机器学习模型以及另一个近来引起热议的基础模型--TimeGPT 进行比较。

TimesFM 架构的指导原则

用于时间序列预测的基础模型应该能够适应不同的环境和时间跨度，同时拥有足够的能力来编码来自大量预训练数据集的所有模式。这一架构的主要指导原则如下：

补丁--分解数据

首先，想一想如何将一本冗长的书分解成易于管理的章节。本模型通过一个称为 “修补 ”的过程对时间序列数据进行类似处理。它不是一次性处理整个序列，而是将数据分成更小、更易于管理的片段，称为 “补丁”。这种方法不仅能加快模型的处理速度，还能帮助它专注于数据中更小、更详细的趋势。反之，将补丁长度扩展到与上下文长度相匹配，则会使解码器训练及其相关效率降低。

纯解码器架构

该模型仅在解码器模式下进行训练。换句话说，在给定一串输入补丁的情况下，下一个补丁将通过模型优化作为过去所有补丁的函数进行预测。与 LLM 相似，这可以在整个上下文窗口中并行完成，在观察到不同数量的输入补丁后自动进行未来预测。

生成较长的预测输出片段

在大型语言模型（LLM）中，输出通常以自动回归的方式产生，一次生成一个标记。然而，研究表明，与多步自动回归解码相比，对于长跨度预测，一次性预测整个跨度会带来更好的准确性。当水平线长度事先未知时，这种直接预测方法就具有挑战性，例如在零镜头预测中，这正是所讨论模型的重点。

为了解决这个问题，作者提出了一个折中方案，即使用比输入补丁更长的输出补丁进行预测。例如，如果输入补丁长度为 32，输出补丁长度为 128，那么模型的训练方法如下：使用前 32 个时间点预测下一个 128 个时间步长，使用前 64 个时间点预测第 65 至 192 个时间步长，使用前 96 个时间点预测第 97 至 224 个时间步长，以此类推。

在推理过程中，如果模型接收到长度为 256 的新时间序列，并负责预测接下来的 256 个时间步，它将首先预测 257 至 384 个时间步。然后，它将使用初始的 256 长度输入和生成的输出来预测时间步长 385 至 512。相比之下，一个输出片段长度等于 32 输入片段长度的模型需要 8 个自动回归步骤才能完成同样的任务，而建议的方法只需要 2 个步骤。

不过，这需要权衡利弊。如果输出片段长度过长，那么处理比输出片段长度更短的时间序列（如预训练数据中的月度或年度时间序列）就会变得非常困难。

模型结构的组成部分

输入

• 对时间序列进行预处理，将输入分割成连续的非重叠片段。
• 然后，通过一个残差块将这些斑块处理成一个大小为 model_dim 的向量。
• 转换器的输入还包括一个二进制掩码。二进制掩码用于表示相应的数据点应该被考虑（0）还是被忽略（1）。
• 残差区块本质上是一个多层感知器区块，有一个带跳过连接的隐藏层。

Transformer架构

该基础模型采用Stacked Transformer方法，即堆叠多个Transformer层，其中每一层都由两个主要部分组成：多头自注意机制和前馈神经网络。

• 多头自我关注： 每个转换层都使用多头自我关注，使模型能够同时关注输入序列的不同部分。这意味着，对于给定的输出标记，模型可以考虑前面标记的多个方面，从而提高捕捉数据中复杂模式和依赖关系的能力。
• 前馈网络： 根据自注意机制，每一层都有一个前馈网络，独立应用于序列中的每个位置。这将进一步处理被关注的信息，并使模型能够学习更高层次的表征。
• 因果注意： 在时间序列预测方面，作者实施了因果注意。这确保了每个输出标记只能关注序列中其前面的标记。这样，模型就能遵守数据的时间顺序，防止来自未来标记的信息（在预测时不应该有）影响当前的预测。
• 堆叠层： 通过堆叠多个转换器层，模型可以逐步建立更抽象的输入数据表示。每一层都会完善前几层所学到的表征，从而使模型能够捕捉不同时间跨度上的复杂模式。
• 超参数： 这使用了两个关键的超参数；
• 模型尺寸： 这决定了每个转换层的表示空间大小。
• 注意头数量： 它规定了模型可以同时关注输入的多少个不同方面。

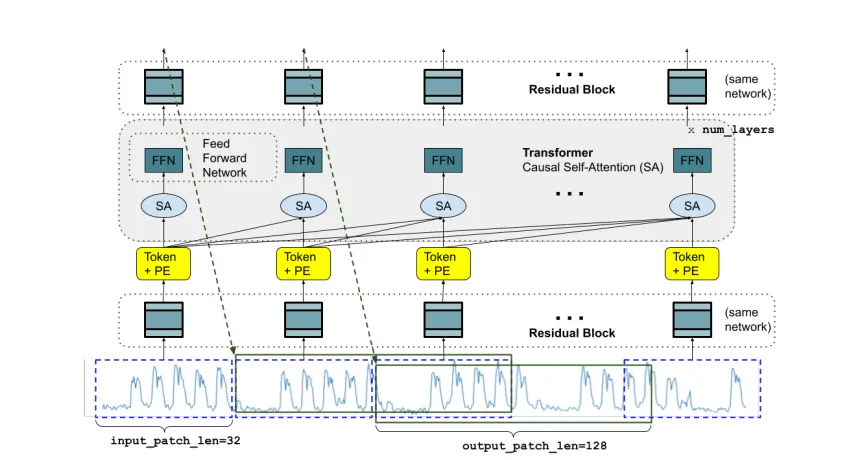
如上图所示，TimesFM 架构接收特定长度的输入时间序列，并将其分解为输入片段。然后，由模型定义中定义的残差块将每个片段处理成矢量，以匹配转换器层的模型维度。然后，矢量被添加到位置编码中。带有位置编码的矢量被输入到叠加的Transformer层中。

SA 指的是自我注意，特别是多头因果注意，而 FFN 指的是转换器中的全连接层。输出标记通过一个残差块映射到一个大小为 output_patch_len 的输出，该输出构成了模型迄今为止看到的最后一个输入补丁之后的时间窗口的预测。

输出层

输出层的任务是将输出标记映射为预测结果。模型只在解码器模式下进行训练，这意味着每个输出标记应预测最后一个输入片段之后的时间序列部分。这里需要注意的是，与许多其他时间序列预测模型不同，这里的输入片段长度不一定等于输出片段长度。这意味着模型可以根据输入片段的信息预测更大的时间序列。

损失函数

本研究使用的损失函数是均方误差（MSE）。本研究以点预测为基础，因此 MSE 可以用来计算训练损失。

训练

模型的训练采用标准的小批量梯度下降法，仅使用解码器。这种方法处理每个时间序列和多个时间序列的时间窗口。

这里使用的屏蔽策略是一个独特之处。对于批次中的每个时间序列，在 0 和 p-1 之间采样一个随机数 r，其中 p 是片段长度。然后创建一个掩码向量 m1:r，其中 m1 设置为 1，其余为 0。这样就屏蔽掉了第一个输入补丁的一部分。这一策略确保模型可以处理从 1 到最大上下文长度的输入上下文。下面的例子可以很好地解释这一点：

• 假设最大上下文长度为 512，补丁长度 p 为 32，r=4。
• 在看到第一个补丁后，输出预测会优化为在看到 32-4=28 个时间点后进行预测。
• 然后对下一个补丁进行优化，在看到 28+32 个时间点后进行预测，以此类推。
• 对所有这样的 r 值进行重复，确保模型可以处理最大 512 的所有上下文长度。

经过训练的模型可以使用自回归解码对任何时间跨度进行预测。

用于训练的数据集

作者使用不同的数据集对 TimesFM 模型进行预训练，以确保它能捕捉广泛的时间模式。他们从谷歌趋势（Google Trends）中获取数据，该数据提供了 15 年内（2007-2022 年）每小时、每天和每周粒度的 22,000 次查询的搜索兴趣数据，共计约 5 亿个时间点。另一个重要数据源是维基页面浏览量（Wiki Pageviews），包括 2012 年至 2023 年维基百科页面的每小时浏览量。该数据集汇总到每日、每周和每月级别，贡献了约 3,000 亿个时间点。

除了真实世界的数据，作者还使用 ARMA、季节模式和趋势等模型生成合成数据，产生了 300 万个合成时间序列，每个序列有 2048 个时间点。其他真实世界的数据源包括 M4 数据集、每小时和 15 分钟的电力数据以及每小时的交通数据，其中 M4 数据集提供了约 10 万个时间序列，交通和电力数据提供了大量时间序列，从而增强了模型的稳健性。

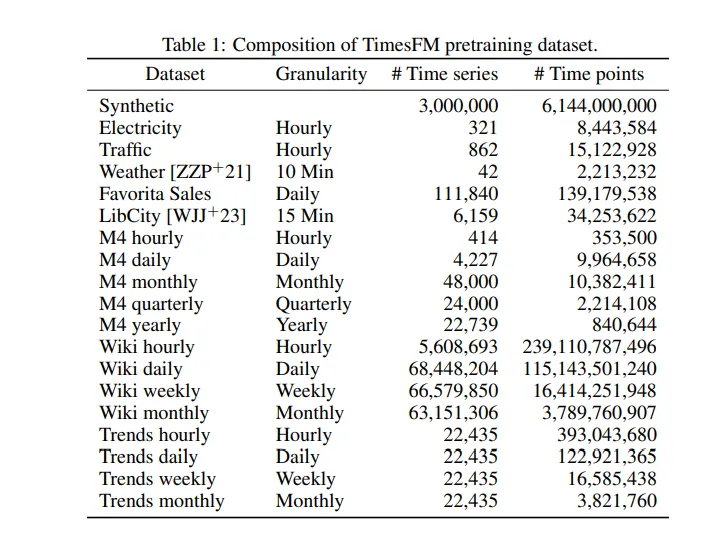
在训练策略方面，作者创建了真实数据集和合成数据集的均衡组合，确保不同粒度（每小时、每天、每周、每月）的平等代表性。训练批次从这些粒度中均匀采样，最小时间序列长度为 256 个时间点，以保持一致性。时间序列按上下文平均值和标准差缩放，以实现输入标准化，每个批次包括 15 个主要时间序列。这种全面的方法可确保 TimesFM 模型为处理不同粒度的各种预测方案做好充分准备。

现在，让我们开始使用它。

实践实施指南

在本节中，我们将了解如何设置用于预测的 TimesFM 模型。此外，我们还将比较该模型与统计模型（AutoETS）、ML 模型（随机森林、XGBoost、LGBM）和基础模型（TimeGPT）的性能。

本研究使用的数据集来自 Kaggle - 每月黄金价格（1979-2021 年） - 18 个不同国家的历史黄金价格。

读取数据

import pandas as pd
df = pd.read_csv("GoldPrices.csv")
df['Date'] = pd.to_datetime(df['Date'])
df = df.set_index('Date').resample('MS').mean()
df = df.reset_index() # Reset index to have 'Date' as a column again
print(df.head())

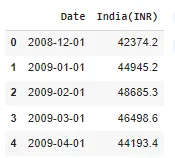
#Let's Visualise the Dataset
import matplotlib.pyplot as plt
import seaborn as sns
sns.set(style="darkgrid")
plt.figure(figsize=(10, 6))
sns.lineplot(x="Date", y='India(INR)', data=df, color='green')
plt.title('Monthly Gold Prices Over Time')
plt.xlabel('Date')
plt.ylabel('Gold Price in INR')
plt.show()

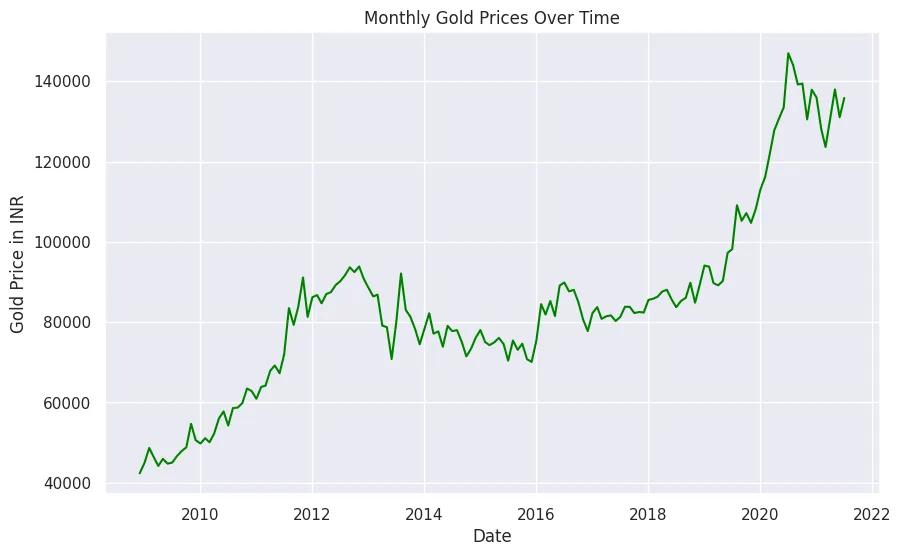
我们将对数据进行季节性分解，以检查趋势和季节性模式。

df.set_index("Date", inplace=True)"Date", inplace=True)
from statsmodels.tsa.seasonal import seasonal_decompose
result = seasonal_decompose(df['India(INR)'])
fig, (ax1, ax2, ax3, ax4) = plt.subplots(4, 1, figsize=(10, 12))
result.observed.plot(ax=ax1, color='green')
ax1.set_ylabel('Observed')
result.trend.plot(ax=ax2, color='green')
ax2.set_ylabel('Trend')
result.seasonal.plot(ax=ax3, color='green')
ax3.set_ylabel('Seasonal')
result.resid.plot(ax=ax4, color='green')
ax4.set_ylabel('Residual')
plt.tight_layout()
plt.show()
df.reset_index(inplace=True)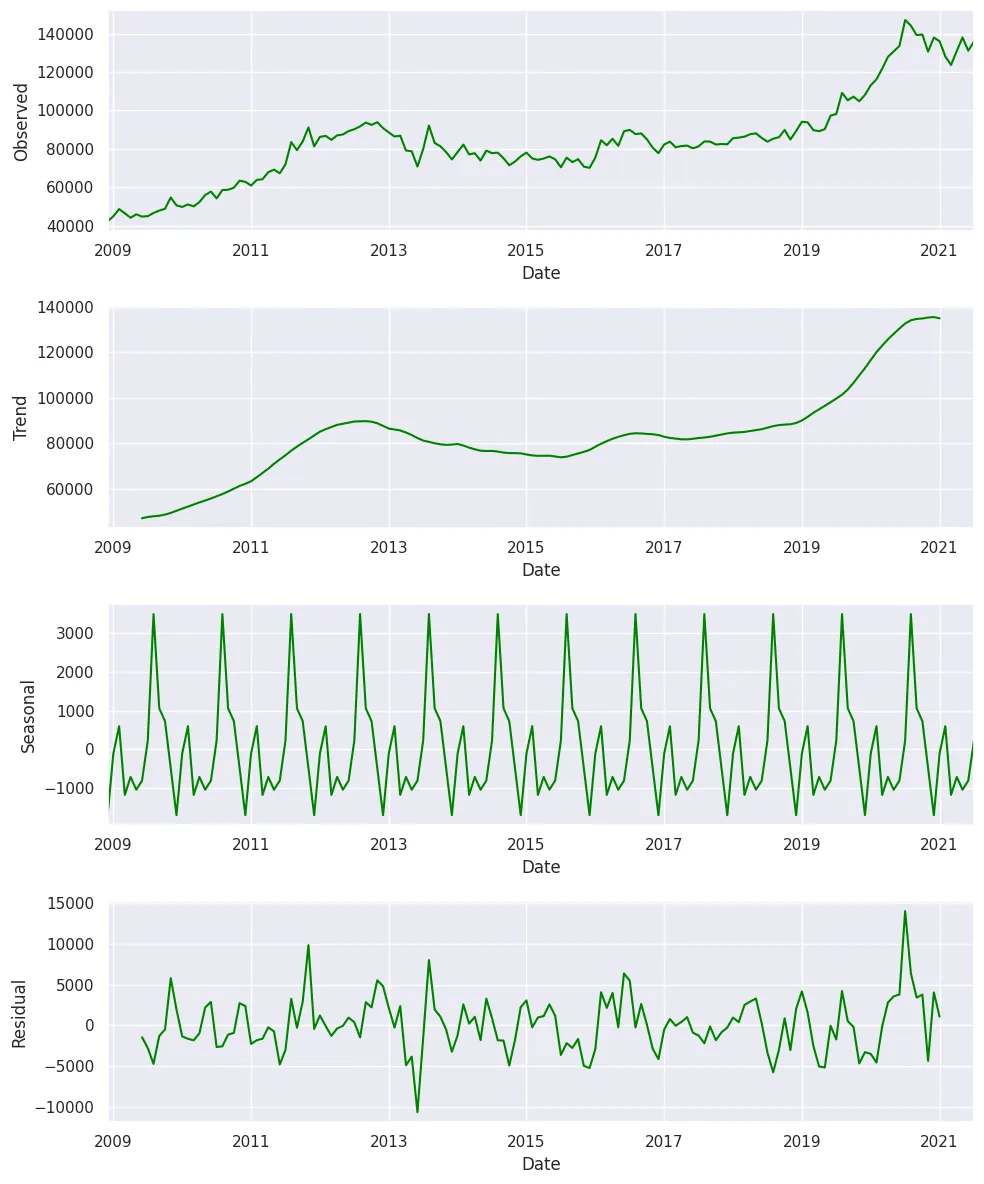

按照模型要求的格式排列数据

因此，Nixtla 模型和 TimesFM 都希望在单变量时间序列数据中有三个不同的列。它们是：

unique_id ：unique_id 列用于识别数据集中的不同时间序列。- 它可以是字符串、整数或类别类型。

• 它代表数据中每个序列的标识符。
• 在处理同一数据集中的多个时间序列时，这一点尤其有用。

ds（日期戳）： ds 列表示时间序列数据的时间部分。- 它应该采用 Pandas 可以解释为日期或时间戳的格式。

• 理想情况下，日期的格式应为 YYYY-MM-DD 或时间戳的格式应为 YYYY-MM-DD HH:MM:SS。
• 此列对于 MLForecast 理解数据的时间方面至关重要。

y（目标变量）： y 列包含你要预测的实际值。- 它应该是数值。

• 这是你要预测的测量值或数量。

df = pd.DataFrame({'unique_id':[1]*len(df),'ds': df["Date"], "y":df['India(INR)']})'unique_id':[1]*len(df),'ds': df["Date"], "y":df['India(INR)']})

现在我们来看看训练-测试分离，我们将使用 128 个数据点进行训练，24 个数据点进行测试。

train_df = df[df['ds'] <= '31-07-2019']'ds'] <= '31-07-2019']
test_df = df[df['ds'] > '31-07-2019']

统计预测

#install statsforecast
!pip install statsforecast
import pandas as pd
from statsforecast import StatsForecast
from statsforecast.models import AutoARIMA, AutoETS
# Define the AutoARIMA model
autoarima = AutoARIMA(season_length=12)  # Annual seasonality for monthly data
# Define the AutoETS model
autoets = AutoETS(season_length=12)  # Annual seasonality for monthly data
# Create StatsForecast object with AutoARIMA
statforecast = StatsForecast(df=train_df,
                         models=[autoarima, autoets],
                         freq='MS',
                         n_jobs=-1)
# Fit the model
statforecast.fit()
# Generate forecasts
sf_forecast = statforecast.forecast(h=24)  # Forecasting for 24 periods

预测结果存储在 sf_forecast 数据帧中。

ML 预测

#install mlforecast
!pip install mlforecast
from mlforecast import MLForecast
from mlforecast.target_transforms import AutoDifferences
from numba import njit
import lightgbm as lgb
import xgboost as xgb
from sklearn.ensemble import RandomForestRegressor
from statsmodels.tsa.seasonal import seasonal_decompose
from mlforecast import MLForecast
from mlforecast.lag_transforms import (
    RollingMean, RollingStd, RollingMin, RollingMax, RollingQuantile,
    SeasonalRollingMean, SeasonalRollingStd, SeasonalRollingMin,
    SeasonalRollingMax, SeasonalRollingQuantile,
    ExpandingMean
)
models = [lgb.LGBMRegressor(verbosity=-1),  # LightGBM regressor with verbosity turned off
    xgb.XGBRegressor(),  # XGBoost regressor with default parameters
    RandomForestRegressor(random_state=0),  # Random Forest regressor with fixed random state for reproducibility
]
fcst = MLForecast(
    models=models,  # List of models to be used for forecasting
    freq='MS',  # Monthly frequency, starting at the beginning of each month
    lags=[1,3,5,7,12],  # Lag features: values from 1, 3, 5, 7, and 12 time steps ago
    lag_transforms={
        1: [  # Transformations applied to lag 1
            RollingMean(window_size=3),  # Rolling mean with a window of 3 time steps
            RollingStd(window_size=3),  # Rolling standard deviation with a window of 3 time steps
            RollingMin(window_size=3),  # Rolling minimum with a window of 3 time steps
            RollingMax(window_size=3),  # Rolling maximum with a window of 3 time steps
            RollingQuantile(p=0.5, window_size=3),  # Rolling median (50th percentile) with a window of 3 time steps
            ExpandingMean()  # Expanding mean (mean of all previous values)
        ],
        6:[  # Transformations applied to lag 6
            RollingMean(window_size=6),  # Rolling mean with a window of 6 time steps
            RollingStd(window_size=6),  # Rolling standard deviation with a window of 6 time steps
            RollingMin(window_size=6),  # Rolling minimum with a window of 6 time steps
            RollingMax(window_size=6),  # Rolling maximum with a window of 6 time steps
            RollingQuantile(p=0.5, window_size=6),  # Rolling median (50th percentile) with a window of 6 time steps
        ],
        12: [  # Transformations applied to lag 12 (likely for yearly seasonality)
            SeasonalRollingMean(season_length=12, window_size=3),  # Seasonal rolling mean with 12-month seasonality and 3-month window
            SeasonalRollingStd(season_length=12, window_size=3),  # Seasonal rolling standard deviation with 12-month seasonality and 3-month window
            SeasonalRollingMin(season_length=12, window_size=3),  # Seasonal rolling minimum with 12-month seasonality and 3-month window
            SeasonalRollingMax(season_length=12, window_size=3),  # Seasonal rolling maximum with 12-month seasonality and 3-month window
            SeasonalRollingQuantile(p=0.5, season_length=12, window_size=3)  # Seasonal rolling median with 12-month seasonality and 3-month window
        ]
    },
    date_features=['year', 'month', 'quarter'],  # Extract year, month, and quarter from the date as features
    target_transforms=[AutoDifferences(max_diffs=3)])
    
    
fcst.fit(train_df)
ml_forecast = fcst.predict(len(test_df))

预测结果存储在 ml_forecast 数据帧中。

TimeGPT 零点预测

!pip install nixtla
from nixtla import NixtlaClient
# Get your API Key at dashboard.nixtla.io
#Instantiate the NixtlaClient
nixtla_client = NixtlaClient(api_key = 'Your_API_Key')
#Get the forecast
timegpt_forecast = nixtla_client.forecast(df = train_df, h=24, freq="M")

TimesFM 预测

在对竞争对手的模型进行预测后，我们将继续探索 TimesFM 模型，这也是本研究的重点。

!pip install timesfm #You might need to restart the kernal to have this installed in your w#You might need to restart the kernal to have this installed in your w
# Initialize the TimesFM model with specified parameters
tfm = timesfm.TimesFm(
    context_len=128,       # Length of the context window for the model
    horizon_len=24,        # Forecasting horizon length
    input_patch_len=32,    # Length of input patches
    output_patch_len=128,  # Length of output patches
    num_layers=20,         
    model_dims=1280,       
)
# Load the pretrained model checkpoint
tfm.load_from_checkpoint(repo_id="google/timesfm-1.0-200m")
# Generate forecasts using the TimesFM model on the given DataFrame
timesfm_forecast = tfm.forecast_on_df(
    inputs=train_df,       # Input DataFrame containing the time-series data for training
    freq="MS",             # Frequency of the time-series data (e.g., monthly start)
    value_name="y",        # Name of the column containing the values to be forecasted
    num_jobs=-1,           # Number of parallel jobs to use for forecasting (-1 uses all available cores)
)
timesfm_forecast = timesfm_forecast[["ds","timesfm"]]

至此，根据本研究中的模型生成预测的代码就完成了。

现在，我们将把所有日期转换成相同的格式，以解决格式不一致的问题，然后合并预测数据框。

# Assuming the DataFrames have a common column 'ds' for the dates
# Convert 'ds' to datetime in all DataFrames if necessary
sf_forecast['ds'] = pd.to_datetime(sf_forecast['ds'])
ml_forecast['ds'] = pd.to_datetime(ml_forecast['ds'])
timegpt_forecast['ds'] = pd.to_datetime(timegpt_forecast['ds'])
timesfm_forecast['ds'] = pd.to_datetime(timesfm_forecast['ds'])
# Now perform the merges
merged_fcst = pd.merge(sf_forecast, ml_forecast, on='ds')
merged_fcst = pd.merge(merged_fcst, timegpt_forecast, on='ds')
merged_fcst = pd.merge(merged_fcst, timesfm_forecast, on='ds')

#Adding the actuals to the dataframe from test_df
merged_fcst = pd.merge(merged_fcst, test_df, on='ds')
#Keep only relevant columns
merged_fcst = merged_fcst[["unique_id", "ds", "AutoARIMA", "AutoETS", "LGBMRegressor", "XGBRegressor", "RandomForestRegressor", "TimeGPT", "timesfm"]]

预测数据帧头如下所示

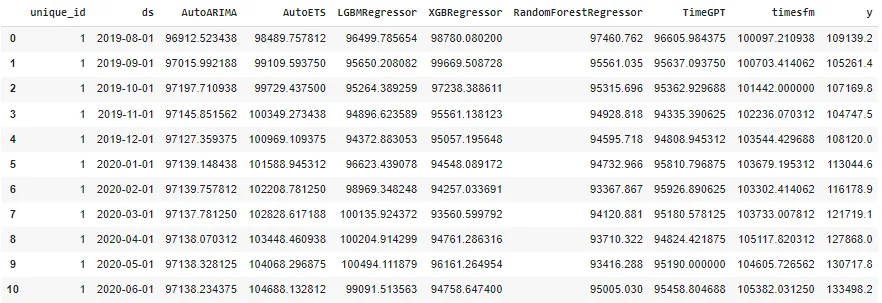
模型评估

import numpy as np
def calculate_error_metrics(actual_values, predicted_values):
    actual_values = np.array(actual_values)
    predicted_values = np.array(predicted_values)
    metrics_dict = {
        'MAE': np.mean(np.abs(actual_values - predicted_values)),
        'RMSE': np.sqrt(np.mean((actual_values - predicted_values)**2)),
        'MAPE': np.mean(np.abs((actual_values - predicted_values) / actual_values)) * 100
    }
    result_df = pd.DataFrame(list(metrics_dict.items()), columns=['Metric', 'Value'])
    return result_df
# Extract 'Weekly_Sales' as actuals
actuals = merged_fcst['y']
error_metrics_dict = {}

for col in merged_fcst.columns[2:-1]:  # Exclude 'Weekly_Sales'
    predicted_values = merged_fcst[col]
    error_metrics_dict[col] = calculate_error_metrics(actuals, predicted_values)['Value'].values  # Extracting 'Value' column

error_metrics_df = pd.DataFrame(error_metrics_dict)
error_metrics_df.insert(0, 'Metric', calculate_error_metrics(actuals, actuals)['Metric'].values)  # Adding 'Metric' column

print(error_metrics_df)

从评估模型中可以看出，对于所评估的数据集，在所比较的模型中，根据 MAE、RMSE 和 MAPE 比较，TimesFM 是仅次于 AutoETS 的最佳模型。

结论

TimesFM 提供了一种可靠的时间序列基础模型方法，可作为预测者的工具箱。TimesFM 采用仅解码器的转换器架构，与许多现有时间序列模型中使用的典型编码器-解码器框架形成鲜明对比。这种设计选择既简化了模型，又保持了预测任务的高性能。从研究中还可以看出，与另一个成功的时间序列基础模型 TimeGPT 相比，该模型在本实验用例中的表现优于前者。