您尚未登录账户
您的企业账号申请正在审核中
【指南】优化函数：变分法
为了找到函数f的最优值，我们需要求解其导数f ' 等于零的点。
变分法可以优化函数，即把其他函数作为输入的函数。其中一个应用就是寻找旅行时间最短的路径。在这里，路径是一个函数 y = f(x)，旅行时间 T 用 f 表示。最优路径，表示为 f*，是在所有可能路径中使 T 最小的函数。
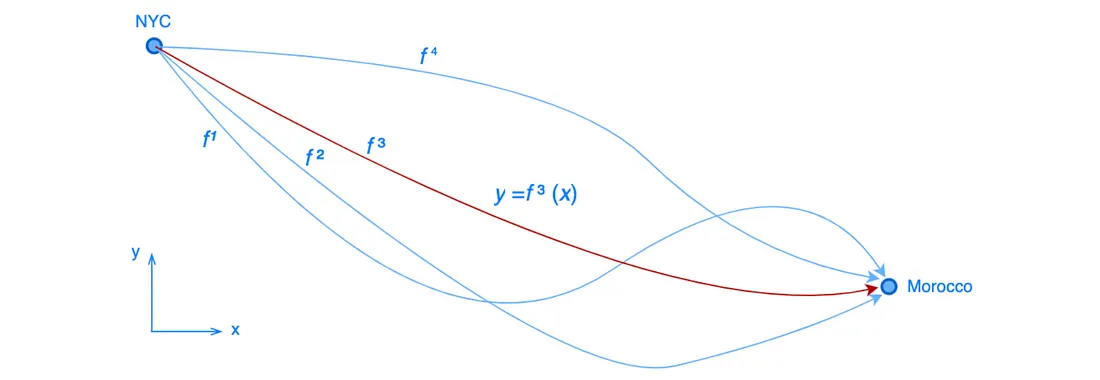
考虑到信风和洋流的影响，让我们研究一下从纽约市到摩洛哥的最快航行路线。对于沿航线的微小位移 ds，航行时间 dt 等于
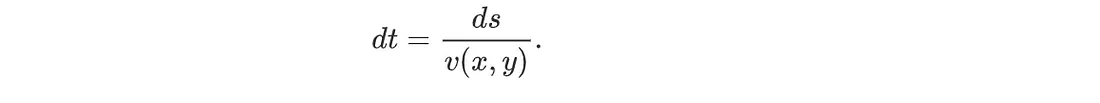
将其与
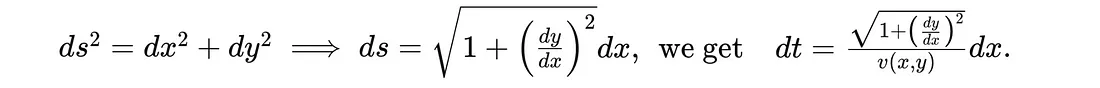
为了求出总的旅行时间 T，我们对从 x₁（纽约市）到 x₂（摩洛哥）的整个路径上的无穷小时间元素 dt 进行积分，得出结果：
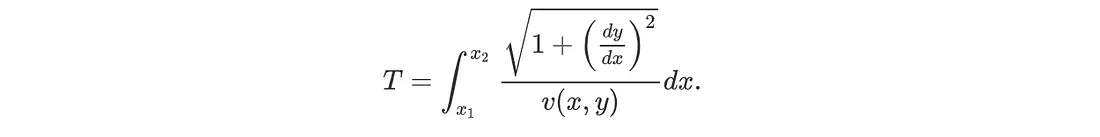
函数 y = f(x) 表示航行路径，T(f) 计算相应的航行时间。这使得 T 成为一个函数--一个将另一个函数作为输入并返回标量值（旅行时间）的函数。我们的目标是找到这个函数的静态函数 f*(x)，代表旅行时间最短的路径。
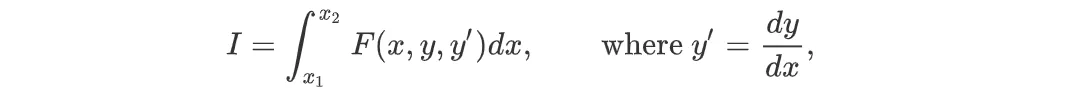
是静止的，边界条件为 y₁= f(x₁) 和 y₂= f(x₂) 。
Euler-Lagrange Equation
假设 y(x) 在满足边界条件的情况下使 I 静止。我们引入一个函数 η(x)。除了边界点为零之外，它是一个完全随机的函数。
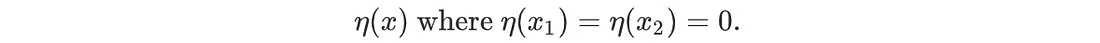
我们定义了另一个函数 ȳ，它可以代表任何函数，但必须满足与 y(x) 相同的边界条件。
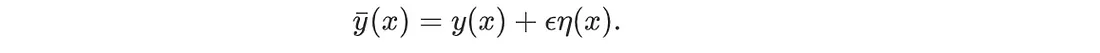
如果 ε = 0，ȳ 和 y(x) 指的是同一个静止函数。
ȳ相对于 ε 的一阶导数和二阶导数为：
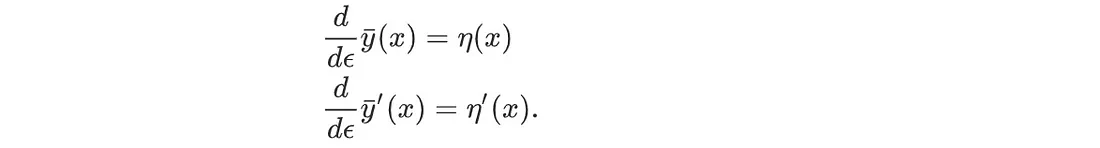
我们稍后会用到它。接下来，我们要找到：
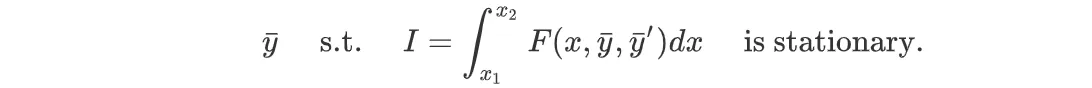
R.H.S. 是对 x 的积分。因此，I 是 ε 的函数，因为所有取决于 x 的其他变量都将被积分。我们只是将这个问题转化为优化单变量 ε，而不是一个函数。因此，我们可以应用常规的微积分方法，将 I 对 ε 的导数设为零，从而找到最优的 ȳ。当 ε 为零时，ȳ 和 y(x) 指的是同一个静止函数。因此，我们将 I 的导数设为 ε=0 时的零。
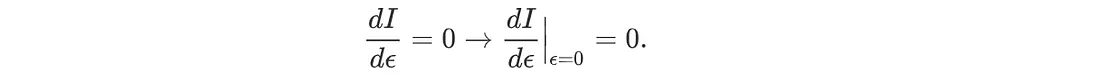
即
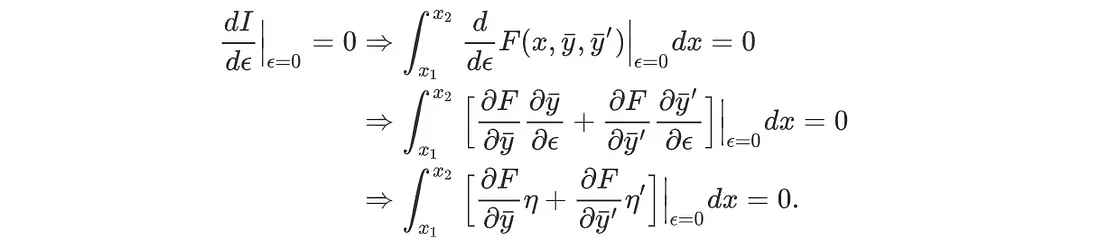
对第二项进行分项积分，得 η(x₁) = η(x₂) = 0。
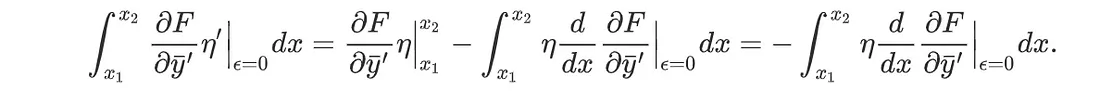
将结果合并，可得：
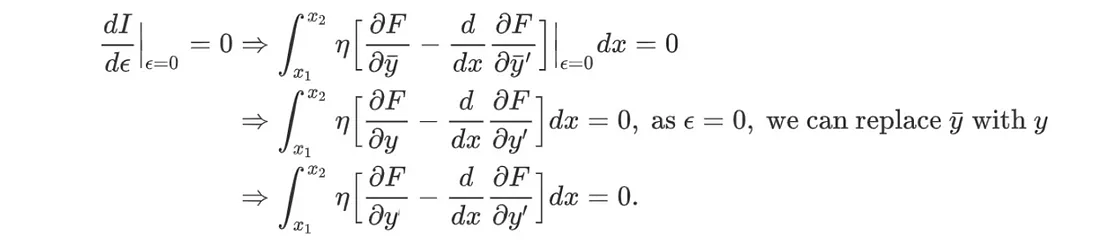
由于 η 是一个相对随机的函数，要使积分为零，我们需要：
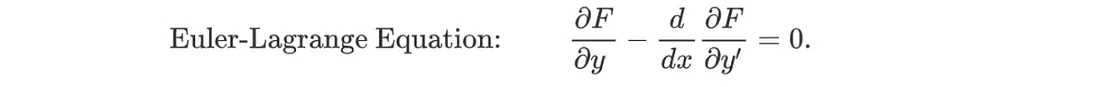
这就是使 F 静止的 y = f(x) 的条件。这就是欧拉-拉格朗日方程。
最短路径
让我们用航行路线问题来演示欧拉-拉格朗日方程。我们将简化问题，假设洋流和风等所有外部因素都不会影响路径，并且帆船以恒定的速度行驶。在优化问题中，任何恒定因素都可以忽略不计。因此，函数 III 简化为：
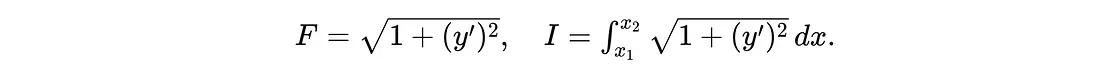
为了找到最短路径，我们应用欧拉-拉格朗日方程。
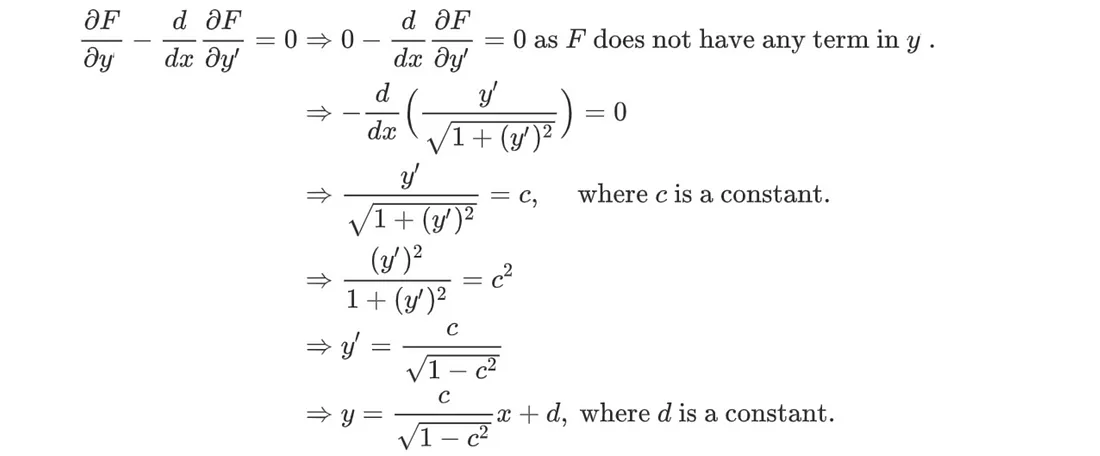
两点之间最短的距离是一条直线。
