虽然决策树作为可解释的模型通常很有效（它们很容易理解），但它们依赖于一种贪婪的构建方法，这种方法可能会产生次优树。在本文中，我们将展示如何生成与标准算法相同（小）规模的分类决策树，但其性能却能大大提高。

动机

在机器学习中，使用可解释模型来解决预测问题通常很有用。与黑盒模型相比，可解释模型至少有两大优势。首先，有了可解释模型，我们就能理解为什么会做出如此具体的预测。其次，我们可以确定在未来（未见）数据中使用该模型是否安全。与黑箱模型相比，可解释模型通常更受青睐，例如，在高风险或高度管制的环境中，使用黑箱模型风险太大。

决策树，至少在限制在合理大小的情况下，是相当容易理解的，而且在足够准确的情况下，是极好的可解释模型。然而，决策树并不总是能达到足够的准确度，而且决策树通常会相当弱，尤其是与 CatBoost、XGBoost 和 LGBM（它们本身就是决策树的提升集合）等针对表格数据的更强模型相比。

此外，在决策树足够准确的情况下，这种准确性往往是通过让决策树长到很大来实现的，从而消除了任何可解释性。一棵深度为 6 的决策树有 2⁶（64）个叶节点，因此实际上有 64 条规则（虽然这些规则相互重叠，但理解这些规则所需的认知负荷并不一定比 64 条完全不同的规则大），而且每条规则都有 6 个条件（其中许多条件往往无关紧要或具有误导性）。因此，这么大的一棵树可能无法被认为是可解释的--不过根据受众的不同，也有可能是可解释的。当然，对于任何受众来说，任何更大的树都是无法解释的。

不过，任何合理的小树，比如深度为 3 或 4 的树，对于大多数目的来说都是可以管理的。事实上，浅层决策树与其他任何模型一样，都是可以解释的。

考虑到决策树作为可解释模型的有效性（即使在实践中并不总能实现高准确性和可解释性），以及可解释 ML 的其他选择较少，对可解释 ML 的大部分研究（包括本文）自然都与如何使决策树成为更有效的可解释模型有关。归根结底，就是要让它们在更小的规模下更加准确。

作为代理模型的可解释模型

除了创建可解释模型，在机器学习中使用可解释模型作为代理模型也很有用。

例如，我们可以为某个预测问题创建一个 CatBoost 或神经网络模型，该模型看起来表现不错。但这个模型（如果是 CatBoost、神经网络或大多数其他现代模型类型）将是不可解释的：我们无法理解它的预测结果。也就是说，通过测试模型，我们可以确定它是否足够准确，但却无法确定它为什么会做出这样的预测。

有鉴于此，将模型投入生产可能可行，也可能不可行。不过，我们可以做的是创建一个工具，尝试估算（并以清晰的方式解释）模型做出预测的原因。其中一种方法就是创建所谓的代理模型。

我们可以创建一个更简单、可解释的模型，如决策树、规则列表、GAM 或 ikNN，来预测黑盒模型的行为。也就是说，代理模型预测黑盒模型将预测的行为。决策树在这方面非常有用。

如果能使代理模型足够准确（能很好地估计黑盒子模型将预测的结果），同时又能对其进行解释，那么它就能为黑盒子模型的行为提供一些洞察，尽管只是近似的洞察：它可以帮助解释黑盒子模型为什么会做出这样的预测，尽管可能并不完全准确，也可能无法预测黑盒子在不寻常的未来数据上的行为。尽管如此，在只需要近似解释的情况下，代理模型对帮助理解黑箱模型还是非常有用的。

在本文的其余部分，我们假设正在创建一个可解释的模型作为实际模型使用，尽管创建一个近似于另一个模型的代理模型也可以以同样的方式工作，而且这也是创建更精确的小型决策树的一个重要应用。

标准决策树使用的贪婪方法

通常，在构建决策树时，我们会从根节点开始，找出最佳的初始分割，创建两个子节点，然后将子节点一分为二，如此循环，直到满足某个停止条件为止。

在训练过程中，决策树中的每个节点都代表训练数据的一部分。根节点代表整个训练集。它会有两个子节点，分别代表训练数据的某个子集（这样两个子集就不会重叠，并覆盖了其父节点的全部训练数据集）。

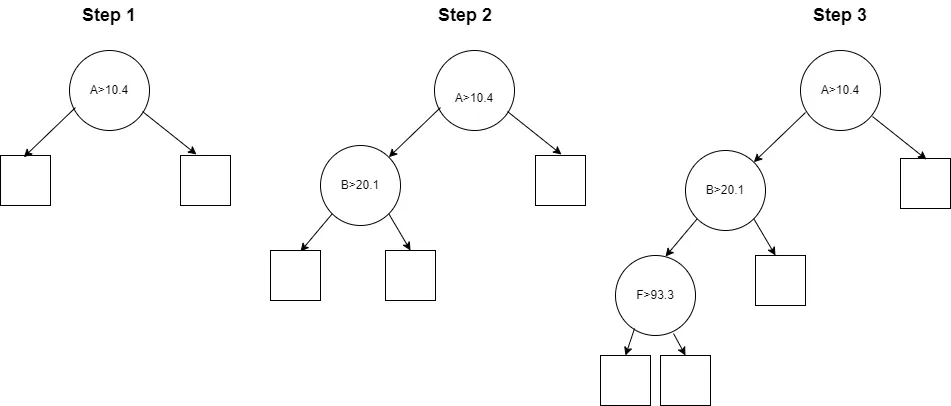
每个内部节点所覆盖的行集会根据与某个特征相关的条件分成两个行子集（通常大小不一样）。在下图中，根节点根据特征 A > 10.4 进行拆分，因此左节点将代表训练数据中特征 A < 10.4 的所有行，右节点将代表训练数据中特征 A ≥ 10.4 的所有行。

为了找到每个内部节点的分割条件，这个过程会选择一个特征和一个分割点，使所谓的信息增益最大化，信息增益与目标值的一致性有关。也就是说：假设有一个分类问题，我们从（根节点）完整的数据集开始。目标列将包含一定比例的各目标类别。我们尝试将数据集分成两个子集，使两个子集在目标类别方面尽可能一致。

例如，在完整数据集中，我们可能有 1000 行数据，其中 A 类 300 行，B 类 300 行，C 类 400 行：

• 左子集：A 类 160 行，B 类 130 行，C 类 210 行
• 右子集：140 个 A 类，170 个 B 类，190 个 C 类

在这里，三个类别在两个子节点中的比例与整个数据集中几乎相同，因此没有（或几乎没有）信息增益。这种拆分方式是不可取的。

另一方面，如果我们对数据进行如下拆分：

• 左子集： 300 个 A 类、5 个 B 类、3 个 C 类
• 右子集：0 个 A 类，295 个 B 类，397 个 C 类

在这种情况下，两个子节点的目标一致性要远远高于整个数据集。左侧子节点几乎只有 A 类，而右侧子节点只有 B 类和 C 类。

然后会选择一个最好的拆分，可能是这里的第二个例子，或者，如果可能的话，选择一个信息增益更高的拆分（两个子节点的目标类别更加一致）。

然后在每个子节点中重复这一过程。在上图中，我们可以看到左侧子节点在特征 B > 20.1 时被拆分，然后其左侧子节点在特征 F > 93.3 时被拆分。

这通常是构建树的合理方法，但绝不能保证找到可能的最佳树。每个决策都是孤立做出的，只考虑该节点所涵盖的数据，而不是整个树。

此外，对于标准决策树来说，在每个节点上选择特征和阈值都是一次性决策（即贪婪算法）：一旦选择了这些分割点，决策树就会受限于对分割点的选择。虽然决策树可以（在较低层次上）补偿树中较高层次上的不良建模选择，但这通常会导致额外的节点，或导致更难理解的分割，因此会降低可解释性，而且可能无法完全缓解上述分割点选择的影响。

虽然决策树所使用的贪婪方法往往是次优的，但它确实可以非常快速地构建决策树。从历史上看，这一点在功率较低的计算机系统中更为重要（在每个节点上评估每个特征中每个可能的分割点实际上是相当大的工作量，即使在现代硬件上速度非常快）。而且，在现代环境下，贪婪算法所带来的速度也非常有用，因为它可以在基于大型决策树集合的模型中快速构建许多树。

不过，要创建一棵既准确又可解释（规模相当小）的决策树，使用贪婪算法的局限性很大。通常情况下，我们可以构建一棵规模有限的决策树，它既能达到很好的准确度，又能大大高于贪婪算法的准确度。

遗传算法

在具体了解决策树之前，我们先简单介绍一下遗传算法。遗传算法被广泛应用于计算机科学领域，通常在开发问题解决方案方面非常有效。遗传算法的工作原理是针对给定的问题生成许多潜在的解决方案，并通过试错找出最佳方案，不过是以一种有指导的、高效的方式，模拟现实世界中的遗传过程。

遗传算法通常从一个问题的若干候选解决方案（通常是随机生成的）开始，然后进行多次迭代，每一轮都会选出最强的候选方案，去掉其他方案，并在现有最佳方案的基础上创建一组新的候选方案。这既可以通过突变（随机修改）现有解决方案来实现，也可以通过将两个或多个解决方案组合成一个新的解决方案来实现，从而模拟现实世界进化过程中的繁殖。

这样，随着时间的推移，一组逐渐强大的候选方案就会出现。并不是每一个新产生的解决方案都比之前产生的解决方案更强，但每一步都会有一部分可能更强，哪怕只是稍强。

在这个过程中，也有可能定期产生全新的随机解决方案。虽然这些解决方案没有突变或强解（最初也是随机产生的）组合的好处，但它们可能会偶然和一些更进化的解决方案一样强。不过这种可能性越来越小，因为通过遗传过程产生的候选方案（并被选为迄今为止的最佳解决方案）越来越进化，越来越适合问题。

在构建决策树时，遗传算法会创建一组候选决策树，选出其中最好的，并对其进行变异和组合（有些新树可能会同时进行这两种操作：从多个现有树中衍生出新的后代，并同时对这些后代进行变异）。这些步骤可以重复任意次数。

每次从一棵或多棵现有树生成一棵新树时，新树都会与之前的树非常相似，但又略有不同。通常情况下，大部分内部节点都是一样的，但会修改一个（或少量）内部节点：改变特征和阈值，或只改变阈值。修改还可能包括添加、删除或重新排列现有的内部节点。每当内部节点被修改时，叶节点中的预测也必须重新计算。

这个过程可能会很慢，需要反复多次才能看到准确性的实质性提高，但在本文所涉及的情况下（创建可解释的决策树），我们可以假设所有决策树都相当小（可解释性的必要条件），最大深度可能在 2 到 5 左右。与我们试图演化大型决策树相比，这种方法能更快地取得进展。

创建更强决策树的其他方法

随着时间的推移，有很多关于决策树遗传算法的建议。本文介绍的解决方案的好处是在 github 上提供了 Python 代码，但它远不是第一个，许多其他解决方案可能更适合你的项目。github 上还有其他几个应用遗传算法构建决策树的项目，也值得研究。但这里介绍的解决方案直接有效，值得在可解释的 ML 有用的地方进行研究。

除遗传算法外，其他旨在提高决策树准确性和可解释性（在受限大小下的准确性）的工作包括最优斯帕斯决策树（Optimal Sparce Decision Trees）、倾斜决策树、遗忘决策树（oblivious Decision Trees）和加法决策树（AdditiveDecisionTrees）。

此外，还有大量与创建可解释规则相关的工作，包括 imodels 和 PRISM-Rules。虽然规则并不完全等同于决策树，但它们可以经常以类似的方式使用，并提供类似的准确性和可解释性。而且，决策树总是可以简单地转换为规则。

一些工具，如 autofeat、ArithmeticFeatures、FormulaFeatures 和 RotationFeatures 也可以与标准树或遗传决策树相结合，以创建更精确的模型。这些模型采用的方法是创建更强大的特征，从而减少树中的节点数量以达到更高的精确度：由于特征更复杂，可解释性会有一些损失，但树通常会大大缩小，从而在可解释性方面获得总体收益（有时是非常大的收益）。

实施细节

决策树对用于训练的数据相当敏感。决策树的不稳定性是出了名的，即使训练数据发生很小的变化，内部表征也会不同。这可能不会明显影响其准确性，但会让人怀疑其捕捉特征与目标之间真实功能的能力。

高方差趋势（基于训练数据微小变化的可变性）也常常导致过度拟合。但有了 GeneticDecisionTree，我们就能利用这一优势生成随机候选模型。

在引擎盖下，GeneticDecisionTree 会生成一组 scikit-learn 决策树，然后将其转换为 GeneticDecisionTrees 内部使用的另一种数据结构（这使得后续的突变和组合操作更加简单）。要创建这些 scikit-learn 决策树，我们只需使用原始训练数据的不同引导样本（同时改变使用的随机种子）进行拟合即可。

我们还改变了样本的大小，以实现进一步的多样性。样本大小基于对数分布，因此我们实际上是在选择样本大小的随机数量级。因此，较小的样本量比较大的样本量更常见，但偶尔也会使用较大的样本量。样本大小最小为 128 行，最大为整个训练集大小的两倍。例如，如果数据集有 100,000 行，我们允许样本大小在 128 和 200,000 之间，在 log(128) 和 log(200,000) 之间均匀抽取一个随机值，然后取这个随机值的指数作为样本大小。

该算法首先创建一小组以这种方式生成的决策树。然后迭代指定次数（默认为五次）。每次迭代：

• 它会随机变异迄今为止创建的得分最高的树（最适合训练数据的树）。在第一次迭代中，它会使用迭代前创建的全部树集。从每一棵表现最好的树中产生大量突变。
  
• 它将迄今为止创建的得分最高的树组合成对。这项工作是以穷举的方式对所有可以组合的最高分树对进行的（详情如下）。
• 使用 scikit-learn 和随机引导样本生成额外的随机树（每次迭代生成的随机树较少，因为与经历过突变和/或组合的模型竞争变得越来越困难）。
• 在循环进行下一次迭代之前，它会选择表现最好的树。其他树则被丢弃。

每次迭代都会生成大量新树。每棵树都会在训练数据上进行评估，以确定其中最强的树，这样下一次迭代开始时就只有少量表现良好的树，而且每次迭代都会在前一次的基础上有所改进。

最后，在执行指定次数的迭代后，选出表现最好的一棵树，用于预测。

如前所述，标准决策树是以纯粹贪婪的方式构建的，只考虑每个内部节点的每个可能拆分的信息增益。而对于遗传决策树来说，每棵新树的构建都可能是部分或完全随机的（scikit-learn 的构建在很大程度上是非随机的，但它是基于随机样本的；突变是纯随机的；组合是纯确定的）。但在拟合过程中做出的重要决定（选择迄今为止生成的最佳模型）与整个树与可用训练数据的拟合有关。这往往会产生比贪婪方法更适合训练的最终结果。

尽管遗传过程很有用，但一个有趣的发现是：即使每次迭代都不进行突变或组合（每次迭代都只是生成随机决策树），遗传决策树也往往比相同（小）规模的标准决策树更准确。

变异和组合操作是可配置的，可以设置为 "假"，以加快执行时间--在这种情况下，我们只需生成一组随机决策树，然后选择最适合训练数据的决策树即可。

这正是我们所期望的：只需尝试决策树内部节点的多组可能选择，其中一些就会比按正常贪婪方式构建的单棵树表现更好。

不过，这是一个非常有趣的发现。同时也非常实用。这意味着：即使没有遗传过程，只要尝试许多潜在的小型决策树来适应训练集，我们几乎总能找到一个比以贪婪方式生长的相同大小的小型决策树更适合数据的决策树。而且往往好得多。事实上，这可能是构建接近最优决策树的一种更实用的方法，而不是专门寻求创建最优决策树，至少对于适合可解释模型的小决策树来说是如此。

在启用突变和组合的情况下，一般经过一到两次迭代后，大多数得分最高的候选决策树（最适合训练数据的树）都将基于突变和/或组合其他强模型。也就是说，突变和组合往往会产生更强的模型。

假设我们创建了一棵大小有限的决策树，那么模型的强大程度就会受到限制--有（尽管在实践中可能无法真正找到）某种树可以创建出与训练数据最匹配的模型。例如，如果有七个内部节点（一个根节点、两个子节点和四个孙节点），那么在拟合树时只需做出七个决定：这七个内部节点中每个节点使用的特征和阈值。

虽然标准决策树不可能找到理想的七个内部节点集，但随机过程（尤其是伴有随机突变和组合的情况下）可以相当快地接近这一理想状态。虽然仍然不太可能达到理想的内部节点集，但它可以接近。

理想树的详尽测试

创建接近最优决策树的另一种方法是使用每一组可能的特征和阈值创建和测试树：对可能的小树进行穷举搜索。

不过，即使是很小的树（例如，七个内部节点），这种方法也很难实现。例如，如果有 10 个特征，那么每个节点中的特征就有 10 个选择（假设特征在树中出现的次数不限）。那么，每个节点的阈值就有大量的选择。

我们可以使用信息增益来选择阈值（在每个节点上保持特征不变，然后选择信息增益最大的阈值）。在只有 10 个特征的情况下，这可能是可行的，但如果特征越多，为每个节点选择特征的组合数仍然会迅速激增。在 20 个特征的情况下，20⁷ 个选择就超过了 10 亿个。

使用一些随机性和遗传过程在一定程度上可以改善这种情况，但几乎在所有情况下，完全穷举搜索都是不可行的。

执行时间

本文介绍的算法远非详尽无遗，但即使在较小的规模下也能生成准确的决策树。

不过，准确度的提高是以时间为代价的，而且这种实现方式只进行了适度的性能优化（例如，它允许内部并行执行操作），速度远低于标准的 scikit-learn 决策树，尤其是在执行多次迭代时。

不过，它的效率还是相当高的，测试发现，与 scikit-learn 决策树相比，通常只需 3 到 5 次迭代就能大幅提高分类效果。对于大多数实际应用来说，其性能是相当合理的。

对于大多数数据集来说，拟合时间仍然只有 1 到 5 分钟，具体取决于数据的大小（行数和列数都有关系）和指定的参数。这与训练标准决策树相比是相当慢的，后者通常不到 1 秒钟。不过，要生成一个可解释的模型，几分钟的时间往往是很有必要的，尤其是在创建一个准确的、可解释的模型往往是相当具有挑战性的情况下。

如果需要，将迭代次数限制在 1 或 2 次，可以减少训练时间，通常仍能取得很好的结果。正如预期的那样，随着时间的推移，使用更多的迭代次数会导致收益递减，过度拟合的几率也会增加。使用 "verbose "设置，可以看到拟合过程的进展，并确定收益何时趋于稳定。

不过，禁用突变和/或组合是减少执行时间的最重要手段。突变和组合允许工具在现有强树的基础上生成变种，通常非常有用（它们生成的树与 scikit-learn 可能生成的树不同），但比简单地根据训练数据的引导样本生成随机树要慢：很大一部分突变的准确率很低（尽管一小部分突变的准确率可能高于其他方法），而根据随机样本生成的树至少都是可行的。

也就是说，对于突变，我们可能需要产生并评估大量的突变，然后才会出现非常强的突变。而组合树的情况则不同，组合树往往比原始树更强。

生成随机决策树

正如建议的那样，在某些情况下，禁用突变和组合，而只根据随机引导样本生成一系列随机树可能是合理的。这种方法不能被视为遗传算法--它只是生成大量的小型决策树，并选择其中表现最好的一棵。不过，如果能通过这种方法达到足够的准确性，这可能就是所需的全部，而且还能缩短训练时间。

也可以先以此为基线，然后测试是否可以通过突变和/或组合找到额外的改进。在使用突变和/或组合时，应将模型设置为至少执行几次迭代，使其有机会逐步改进随机生成的树。

在此，我们还应强调这种方法（创建许多相似但随机的树，不使用任何遗传过程）与创建随机森林（RandomForest）的相似性--随机森林也是基于一组决策树，每棵树都是在随机引导样本上训练出来的。不过，RandomForests 会使用创建的所有决策树，并将它们的预测结果结合起来，而 GeneticDecisionTree 只保留其中最强的一棵决策树。

变异

下面我们将具体介绍遗传决策树的变异和组合过程是如何工作的。

遗传决策树目前支持的突变过程非常简单。它只允许修改内部节点使用的阈值，保持所有节点使用的特征相同。

在突变过程中，会选择一棵表现良好的树，并创建该树的新副本，除了一个内部节点使用的阈值外，其他都是一样的。要修改的内部节点是随机选择的。它在树中的位置越高，新阈值与之前阈值的差异越大，新树与原始树的差异就越大。

这种方法的效果出奇的好，往往能大大改变其下面两个子节点（以及所选节点下面的两个子树）所使用的训练数据。

在突变之前，每棵树都从 scikit-learn 指定的阈值开始，而这些阈值的选择完全基于信息增益（不考虑树的整体性）。即使保持树的其余部分不变，修改这些阈值也能有效地诱导出截然不同的树，而这些树的表现往往更胜一筹。虽然大多数变异树与原始树相比并没有改进，但通过对每棵树进行适量的变异尝试，通常可以发现改进之处。

组合

目前支持的另一种修改形式是组合两棵表现良好的决策树。为此，我们会选取上一次迭代中发现的前二十棵树，并尝试将其中的每一对组合起来。如果两棵树的根节点使用了相同的特征，就有可能进行组合。

例如，假设树 1 和树 2（下图中最上面一行的两棵树）是目前发现的表现最好的树。

图中一共显示了四棵树： 树 1、树 2 以及由这两棵树创建的两棵树。内部节点用圆形表示，叶子节点用方形表示。

树 1 的根节点在特征 A > 10.4 时出现分裂，树 2 的根节点在特征 A > 10.8 时出现分裂。因此，我们可以将这两棵树合并：它们的根节点都使用特征 A。

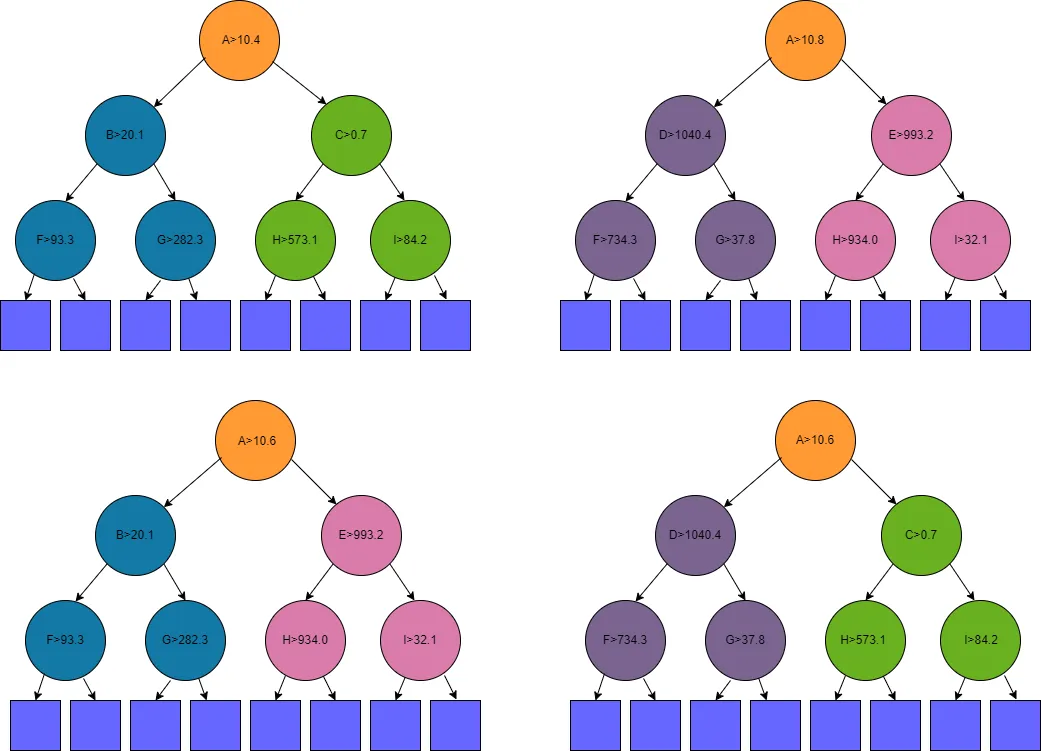
然后，我们创建两棵新树。在这两棵新树上，根节点中的分叉取两棵原树的平均值，因此在本例中，两棵新树（如图中下行所示）的根节点中都有特征 A > 10.6。

第一棵新树将包含树 1 的左侧子树（树 1 根节点下的左侧子树，用蓝色绘制）和树 2 的右侧子树（用粉色绘制）。另一棵新树将包含树 2 的左子树（紫色）和树 1 的右子树（绿色）。

在这个例子中，树 1 和树 2 都只有 3 层内部节点。在其他例子中，子树可能更大一些，但如果是这样，也可能只有一到两层的深度。无论子树的大小或形状如何，思路都是一样的。

以这种方式进行组合，除了树根外，实际上就是一棵树的一半和另一棵树的一半，其原理是：如果两棵树都很强，那么：

• 如果两棵树都很强，那么（虽然不一定）根节点中共同选择的特征也很强。此外，在两者选择的特征点之间选择一个分割点可能更好。在上面的例子中，我们使用了 10.6，它介于父树使用的 10.4 和 10.8 之间。
• 虽然两棵树都很强，但可能都不是最佳选择。如果有区别的话，区别就在于两个子树。树 1 可能同时拥有较强的左侧子树和右侧子树，在这种情况下，与树 2 结合就不可能战胜树 1。但是，如果树 1 有较强的左子树，而树 2 有较强的右子树，那么利用这一点创建一棵新树，就会产生一棵比树 1 或树 2 都强的树。

可以想象，我们还可以用其他方法来组合两棵树，通过遗传算法生成决策树的其他工具也会使用其他方法来组合树。但简单地从一棵树中提取一棵子树，再从另一棵树中提取另一棵子树，是一种非常直接的方法，而且这种方法也很吸引人。

未来的版本将允许使用根节点以外的节点进行组合，不过在这种情况下效果会比较小--我们将保留一棵树的大部分，替换另一棵树的一小部分，因此产生的新树与原来的树区别不大。不过，这仍然是一种有价值的组合形式，未来将得到支持。

过度拟合

决策树通常会过拟合，遗传决策树也可能会。与大多数模型一样，遗传决策树试图尽可能地与训练数据拟合，这可能会导致它的泛化效果比其他相同大小的决策树差。

不过，由于决策树的大小一般都很小，而且决策树的生长深度不能超过指定的最大深度，因此过度拟合是有限的。生成的每一棵候选决策树都具有相同的复杂度（或几乎相同--有些路径可能无法扩展到允许的最大深度，因此有些树可能比其他树略小），因此过拟合的可能性大致相同。

不过，对于任何模型，我们都建议对遗传决策树进行调整，以找到对数据最有效的模型。

回归

遗传决策树支持分类和回归，但更适合分类。一般来说，回归函数很难使用浅层决策树建模，因为需要预测连续的数值，而每个叶节点只能预测一个数值。

例如，一棵有八个叶节点的树只能预测八个唯一的值。对于分类问题来说，这通常已经足够了（假设不同目标类别的数量在 8 个以下），但对于回归问题来说，只能产生非常近似的预测结果。对于回归问题，即使是简单的函数，一般也需要非常深的树才能产生准确的结果。树的深度越深，预测结果就越精确。

只有当数据的目标列中只有少量不同的值，或者这些值分布在少量聚类中，且每个聚类的范围都相当小时，使用小树进行回归才是可行的。

遗传决策树可以将最大深度设置得很高，从而建立精确的模型，通常比标准决策树高得多，但这样的决策树就无法解释。而且，虽然准确率通常很高，但仍可能无法与 XGBoost、LGBM 或 CatBoost 等强大的模型相媲美。有鉴于此，用于回归的遗传决策树（或为回归创建精确浅层决策树的任何尝试）通常是不可行的。

安装

遗传决策树的 github 页面是：https://github.com/Brett-Kennedy/GeneticDecisionTree。

安装时，只需下载单个 genetic_decision_tree.py 文件并将其导入到项目中即可。

github 页面还提供了一些示例笔记本，但只需阅读简单示例笔记本，就能了解如何使用该工具以及 API 的一些示例。github 页面还记录了 API，但这些 API 相对简单，提供的签名与 scikit-learn 的 DecisionTreeClassifier 类似，但规模较小。

示例

以下示例摘自 github 页面提供的 Simple_Examples 笔记本。它加载了一个数据集，进行了训练-测试拆分，拟合了一棵遗传决策树，创建了预测结果，并输出了准确率，这里使用的是 F1 宏分数。

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import f1_score
from sklearn.datasets import load_wine
from genetic_decision_tree import GeneticDecisionTree
data = load_wine()
df = pd.DataFrame(data.data)
df.columns = data.feature_names
y_true = data.target
X_train, X_test, y_train, y_test = train_test_split(df, y_true, test_size=0.3, random_state=42)
gdt = GeneticDecisionTree(max_depth=2, max_iterations=5, allow_mutate=True, allow_combine=True, verbose=True)
gdt.fit(X_train, y_train)
y_pred = gdt.predict(X_test)
print("Genetic DT:", f1_score(y_test, y_pred, average='macro'))

GeneticDecisionTree 是一个同时用于分类和回归的类。它从目标数据中推断出数据类型，并在内部处理回归和分类之间的区别。如前所述，它更适合用于分类，但在需要时也可直接用于回归。

与 scikit-learn 的决策树类似，GeneticDecisionTree 也提供了 export_tree() API。在使用深度为 2 的葡萄酒数据集时，GeneticDecisionTree 在保持测试集上的 F1 宏得分为 0.97，而 scikit-learn 决策树的 F1 宏得分为 0.88。GeneticDecisionTree生成的决策树是：

IF flavanoids < 1.40001.4000
| IF color_intensity < 3.7250
| | 1
| ELSE color_intensity > 3.7250
| | 2
ELSE flavanoids > 1.4000
| IF proline < 724.5000
| | 1
| ELSE proline > 724.5000
| | 0

分类测试

github 页面提供了对 GeneticDecisionTrees 的广泛测试。该测试使用了 OpenML 中的大量测试集，并为每个测试集创建了一棵标准（scikit-learn）决策树和四棵 GeneticDecisionTrees：允许突变和允许组合的每种组合（既不支持突变，也不支持组合）。在所有情况下，最大深度都是 4。

几乎在所有情况下，基因决策树的至少一种变体，通常是全部四种变体，都大大优于标准决策树。这些测试使用 F1 宏分数来比较模型。这里显示的是其中的一个子集：

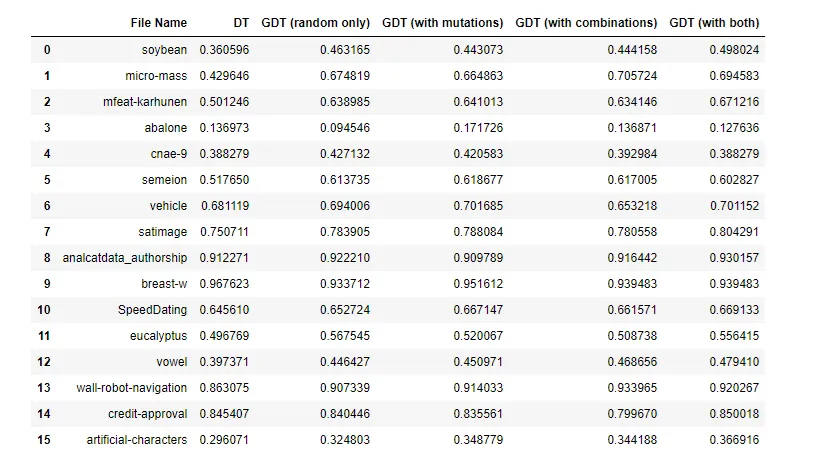
在大多数情况下，启用突变或组合，或同时启用突变和组合，都比简单地生成随机决策树要好。

由于测试的案例较多，运行本笔记本的速度相当慢。此外，它也不是一个确定的评估：它只使用了有限的测试文件集，只使用了除最大深度之外的默认参数，并且只测试了 F1 宏得分。不过，它确实证明了遗传决策树在许多情况下都能成为有效且可解释的模型。

结论

在许多情况下，最好使用可解释模型（或黑盒模型和可解释代理模型），在这些情况下，浅层决策树往往是最佳选择之一。不过，标准决策树的生成方式可能不够理想，从而导致准确率较低，尤其是对于我们限制其大小的决策树而言。

这里演示的简单过程是根据训练数据的随机样本生成许多决策树，然后找出最适合训练数据的决策树，与之相比，这一过程具有显著优势。

事实上，最大的发现是，根据不同的随机样本生成一组决策树，其效果几乎与本文中的遗传方法相同。不过，如果在未来版本的代码库中添加更多的突变和组合，或者执行大量的迭代，这一发现可能就无法继续保持下去了。

除了生成许多树之外，允许采用遗传过程，即训练执行多次迭代，每次都对迄今为止发现的表现最好的树进行变异和组合，往往可以进一步改善这种情况。