softmax、ReLU、sigmoid 和 tanh 函数有什么共同点？它们都是激活函数，而且都是非线性的。但为什么我们首先需要激活函数，尤其是非线性激活函数呢？这其中有传统的推理，也有新的视角。

传统的推理是这样的：如果没有非线性激活函数，深度神经网络就只是矩阵乘法和添加偏置的组合。这些都是线性变换，你可以用线性代数证明，线性变换的组合只是另一种线性变换。

因此，无论我们将多少线性层堆叠在一起，如果没有激活函数，我们的整个模型都不会比线性回归更好。它将完全无法捕捉非线性关系，甚至是像 XOR 这样的简单关系。

输入激活函数：通过让模型学习非线性函数，我们获得了模拟现实世界中各种复杂关系的能力。

今天，我想与大家分享另一种看待激活函数必要性的方法，以及它所揭示的深度学习模型的内部工作原理。

简而言之，我想与大家分享的是：我们通常构建深度学习分类器的方式会在模型中产生归纳偏差。具体来说，为输出使用线性层意味着模型的其他部分必须找到输入的线性可分离变换。这背后的直觉可能真的很有用，所以我将分享一些例子，希望能澄清一些专业术语。

传统解释

让我们通过一个例子来重温非线性激活函数的传统原理。我们来看一个简单的例子： XOR。

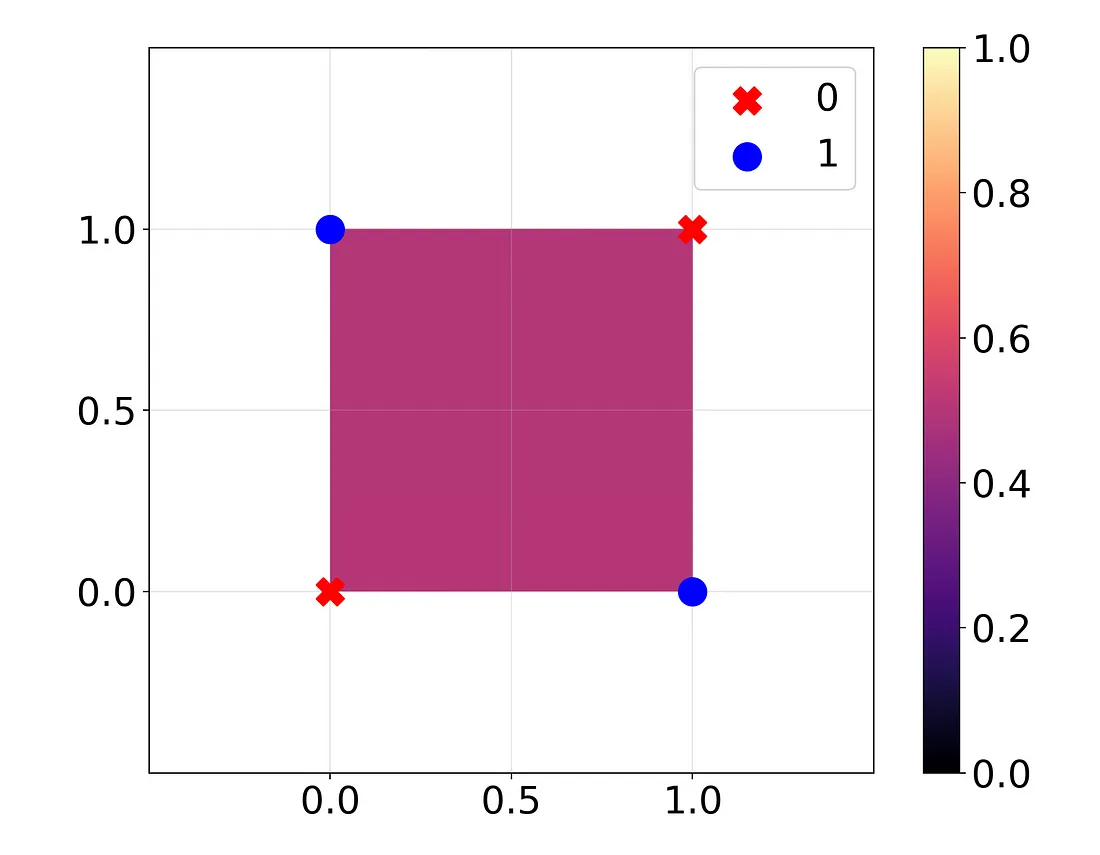
在这里，我用两个二进制输入对 XOR 函数训练了一个线性回归模型（地面真实值用点表示）。我将回归的输出绘制成背景色。回归完全没有学到任何东西：它在所有情况下都猜测为 0.5。

现在，我不再使用线性模型，而是使用 MSE 损失训练一个非常基本的深度学习模型。只有一个线性层，包含两个神经元，然后是 ReLU 激活函数，最后是输出神经元。为了保持简单，我将只使用权重，不使用偏置。

现在怎么办？

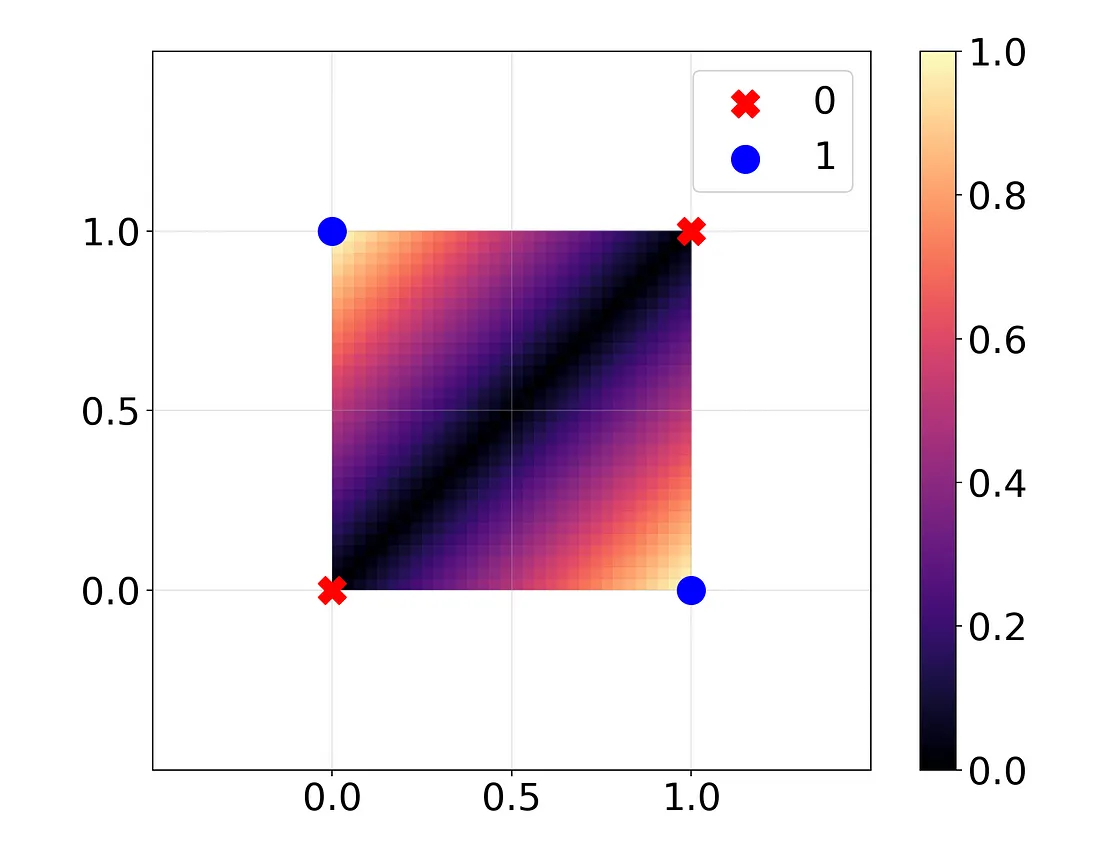
哇，现在完美了！看起来怎么样？

Layer 1 weight: [[ 1.1485, -1.1486],
                [-1.0205,  1.0189]]
(ReLU)
Layer 2 weight: [[0.8707, 0.9815]]

因此，对于两个输入 x 和 y，我们的输出是：

这真的很像

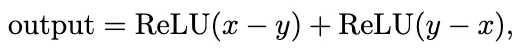
你可以验证这正是输入 x、y 在 {0, 1} 中的 XOR 函数。

如果没有 ReLU，我们就可以将模型简化为 0.001y - 0.13x，这是一个完全不起作用的线性函数。这就是传统的解释：由于 XOR 本身是一个非线性函数，因此任何线性函数都无法对其进行精确建模。即使是线性函数的组合也不行，因为那只是另一个线性函数。引入非线性 ReLU 函数可以让我们捕捉到非线性关系。

深入挖掘： 归纳偏差

现在，我们将研究同一个 XOR 模型，但我们将从另一个视角来看待它，并更好地了解这个模型的归纳偏差。

什么是归纳偏差？任何问题都有多种解决方法。从本质上讲，归纳偏差是模型架构中内置的一种东西，它会引导模型选择特定的方法来解决问题，而不是其他任何方法。

在这个深度学习模型中，我们的最后一层是一个简单的线性层。这意味着，除非模型在最后一层之前的输出可以通过线性回归求解，否则我们的模型根本无法工作。换句话说，输出前的最终隐藏状态必须是线性可分离的，模型才能工作。这种归纳偏差是我们模型架构的属性，而不是 XOR 函数的属性。

幸运的是，在这个模型中，我们的隐藏状态只有两个神经元。因此，我们可以将其可视化为两个维度。它看起来像什么？

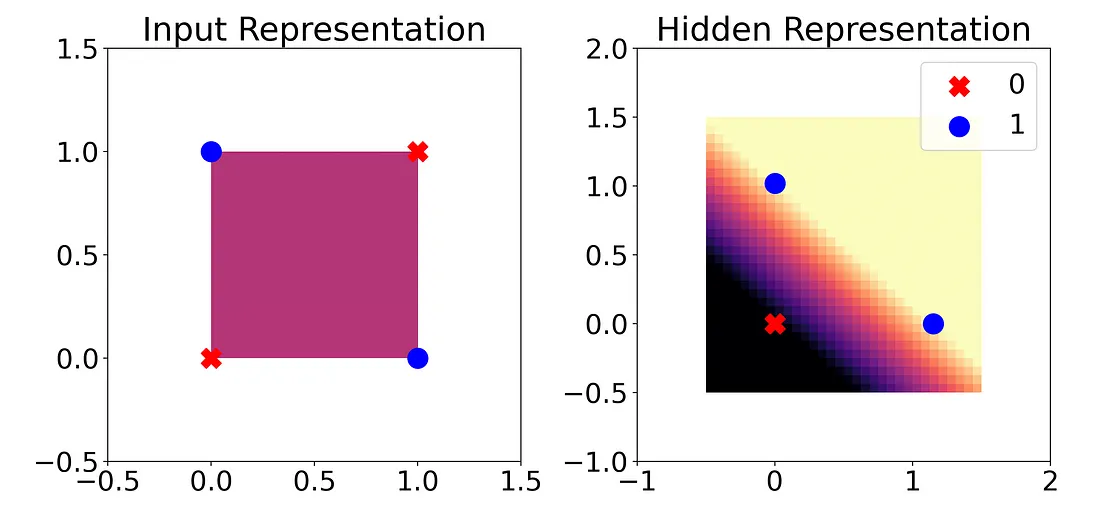
正如我们之前所看到的，单靠线性回归模型并不能有效地处理 XOR 输入。但是，一旦我们将输入通过神经网络的第一层和 ReLU，我们的输出类别就能被一条线整齐地分开（线性可分）。这意味着线性回归现在可以起作用了，事实上，我们的最后一层实际上就是在执行这种线性回归。

现在，这对我们的归纳偏差有何启示？既然我们的最后一层是线性层，那么这一层之前的表示必须至少近似于线性可分离。否则，作为线性回归的最后一层就会失败。

线性分类器探针

对于 XOR 模型来说，这可能只是我们之前看到的传统观点的微不足道的扩展。但对于更复杂的模型，这又是如何实现的呢？随着模型的深入，我们可以通过这种方式来观察非线性，从而获得更多的洞察力。Guillaume Alain 和 Yoshua Bengio 的这篇论文利用线性分类器探针研究了这一想法。

在很多情况下，比如 MNIST 手写数字，预测所需的所有信息都已存在于输入中：只需对其进行处理即可。阿兰和本吉奥注意到，随着我们对模型的深入研究，我们在每一层获得的信息实际上越来越少，而不是越来越多。但好的一面是，在每一层，我们所拥有的信息都变得 “更容易使用”。我们的意思是，在每个隐藏层之后，信息的线性可分性会越来越高。

我们怎样才能知道模型的表示在每一层之后的线性可分离程度呢？阿兰和本吉奥建议使用他们所谓的线性分类器探针。他们的想法是，在每一层之后，我们使用该层的隐藏状态作为输入，训练线性回归来预测最终输出。

Alain 和 Bengio 将这一方法应用到了以 MNIST 手写数字为基础进行训练的卷积神经网络中：在每次卷积、ReLU 和池化之前和之后，他们都添加了一个线性探针。他们发现，从一个探针到下一个探针，测试误差几乎总是在减少，这表明线性可分性在增加。

为什么数据变得线性可分，而不是 “多项式可分 ”或其他？因为最后一层是线性的，所以我们使用的损失函数会对模型中的所有其他层施加压力，使它们协同工作，为最后一层的预测创建一个线性可分的表示。

这个想法是否也适用于大型语言模型（LLM）？事实上，确实如此。Jin 等人（2024 年）使用线性分类器探测来演示 LLM 如何学习各种概念。他们发现，一些简单的概念，例如某个城市是否是某个国家的首都，在模型的早期就可以线性分离：只需要几个非线性激活就可以建立这些关系的模型。相比之下，许多推理技能要到模型的后期才具有线性可分性，或者对于较小的模型根本不具有线性可分性。

结论

当我们使用激活函数时，就会在深度学习模型中引入非线性。知道这一点当然很好，但我们可以通过多种方式解释线性和非线性的后果，从而获得更多价值。

上述解释着眼于整个模型，而一个有用的思维模型则以深度学习模型的最后一个线性层为中心。既然这是一个线性层，那么在它之前的任何东西都必须是线性可分离的；否则，模型就无法工作。因此，在训练时，模型的其余各层将共同寻找一个线性表示，供最后一层用于预测。