在这篇文章中，我想展示根据所需的物理特性作为分子生成器使用的变压器网络。在某种程度上，这就像最初用于文本翻译的变压器模型，只不过我们的输入将是一组所需的物理特性，而 “翻译 ”后的输出将是分子结构。作为输入的一组物理特性并不是一个序列，因此我们将为编码器设计一个明显不同的网络架构。虽然分子本质上是一个图，而不是序列，但我们可以将分子的 SMILES 符号视为序列。在本文中，我将简要介绍Transformer网络，然后在 pytorch 中从头开始实现它。我知道你现在可以直接导入Transformer模型并采用黑盒方法，但从头开始实现这些网络会让你更深入地理解其基本原理，这对于需要新挑战、定制和优化的问题尤为重要；黑盒方法是不够的，可能很快就会自动化。

Transformer网络；多头关注

Transformer网络的核心是多头关注机制，它能让模型同时关注序列的所有部分。RNN、LSTM、GRU（以及它们的其他变体）的递归性质非常好，因为它们对数据的摄取本质上是连续的，无需进一步处理，但一次生成一个输出意味着训练大型模型的计算时间会非常长，而且由于梯度消失，性能也会成为问题。多头注意力能够克服这些限制。为了获得注意力机制背后的直觉，请考虑一个时间序列 X

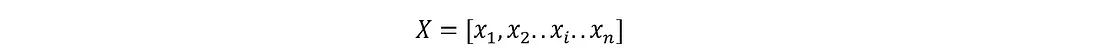
其中 xi 是标量值（对于语言和其他应用，xi 可能是嵌入向量而不是标量）。假设你想预测数列中的下一个值；你最关注当前数列中的哪个值？所有值的平均值？这就是注意力层非常有用的地方，它可以了解需要关注哪些值以及关注的程度，从而预测未来的值。注意力机制建立在由输入序列 X 衍生出的三个主要组成部分之上，包括查询 (q)、键 (k) 和值 (v)，其计算方法如下：

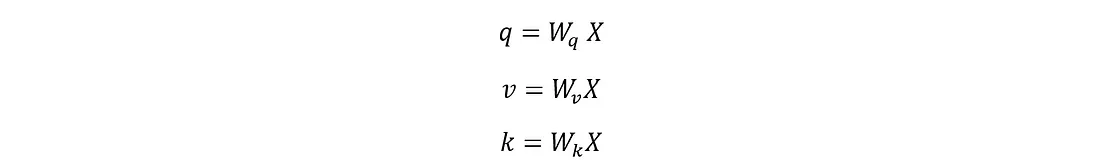
其中，Wq、Wv、Wk 都是在训练过程中确定的可学习矩阵。随后可以确定点积关注度 (q.k)，计算每个查询和所有键之间的关注度得分，然后使用这些得分对相应的值进行加权。注意力分数通过一个 softmax 函数得到注意力权重，它是密钥的概率分布。这些注意力权重与值矩阵一起用于确定注意力层（也称为头部）

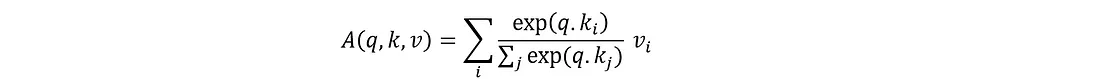
如果你不熟悉这些方程组和线性代数，我们可以将过程的每一步形象化：

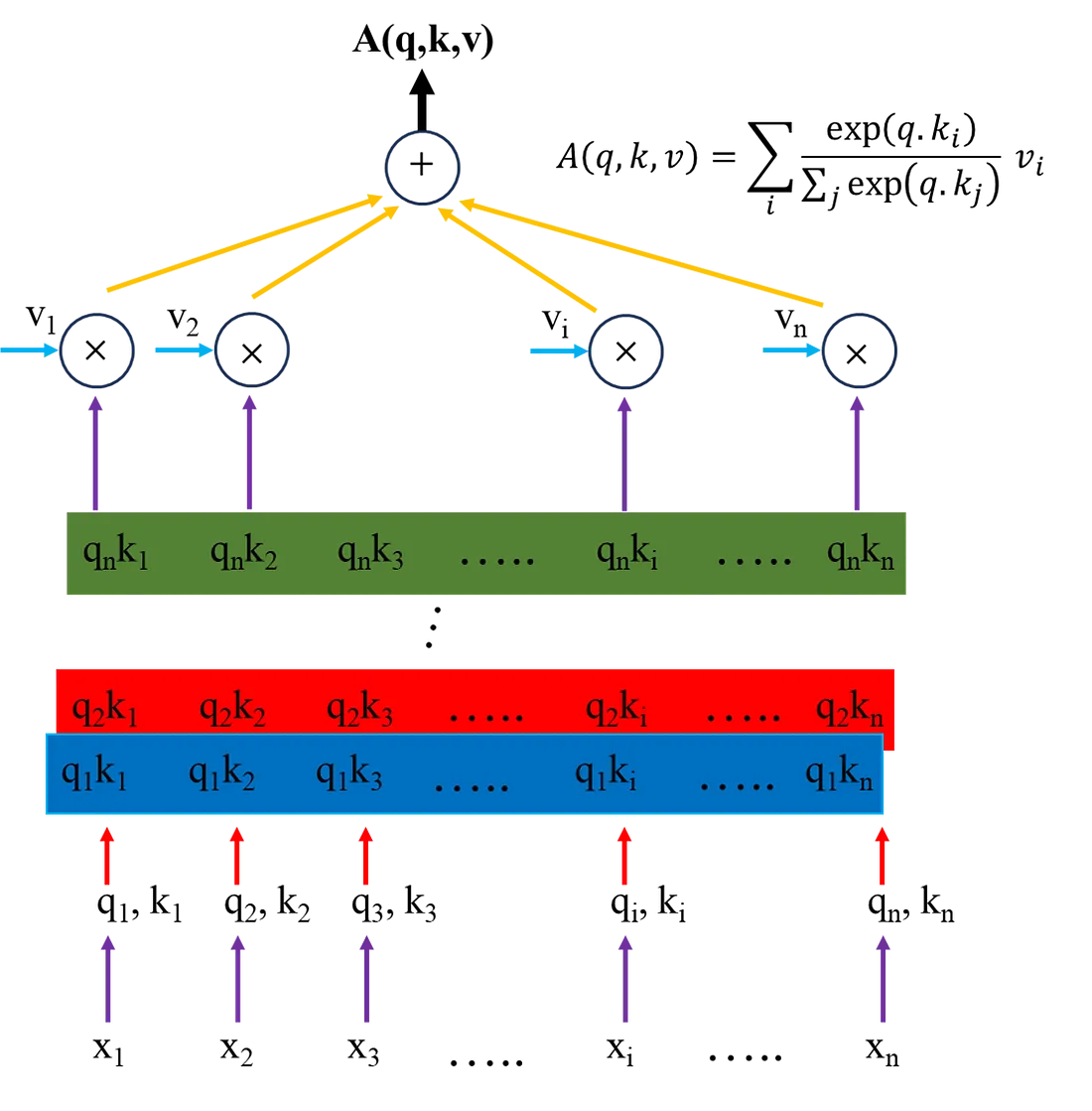
这涵盖了自我注意力的基础，但在实践中，我们会使用多头注意力，即多次运行上述注意力机制，每次都使用不同的可学习矩阵（即不同的 Wq、Wk、Wv）。让我们在 pytorch 中编写相关代码，值得仔细阅读代码，以确保你完全理解上述方程。我提供了一些注释以指导读者

# MULTIHEAD ATTENTION 
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np
class MultiHeadAttention(nn.Module):
    def __init__(self, d_model, num_heads):
        super(MultiHeadAttention, self).__init__()
        try:
            assert d_model % num_heads == 0
        except Exception as e:
            logger.error("dimension of the embedding model is not divisable by number of heads")
        self.d_models = d_model
        self.num_heads = num_heads
        self.depth = d_model // num_heads
        # The query, key, value learnable matrices
        self.Wq = nn.Linear(d_model, d_model)
        self.Wk = nn.Linear(d_model, d_model)
        self.Wv = nn.Linear(d_model, d_model)
        self.FCLayer = nn.Linear(d_model, d_model)
    def split_embedding_perHead(self,x):
        # x shape is (batch_size, seq_len, d_model)
        (batch_size, seq_len, d_model) = x.shape
        # let's reshape to (batch_size, seq_len, num_heads, depth)
        x = x.view(batch_size, -1, self.num_heads, self.depth)
        # changing the dimensions order to:(batch_size, num_heads, seq_len, depth)
        x = x.permute(0,2,1,3)
        return x
    
    def cal_attention(self,q,k,v,mask):
        qk = torch.matmul(q, k.permute(0,1,3,2))
        dk=torch.tensor(k.shape[-1], dtype=torch.float32)
        #dk is a tensor scalar!
        attention = qk/torch.sqrt(dk)
        if mask is not None:
            attention += (mask*-1e9)
        attention_weights = F.softmax(attention, dim=-1) # should be applied along the sequence which is the 3rd dimension
        output = torch.matmul(attention_weights, v)
        return output, attention_weights
    
    def forward(self, v,k,q,mask):
        batch_size = q.shape[0]
        q = self.split_embedding_perHead(self.Wq(q))
        k = self.split_embedding_perHead(self.Wk(k))
        v = self.split_embedding_perHead(self.Wv(v))
        attention,atten_weights = self.cal_attention(q,k,v,mask)
        attention = attention.permute(0,2,1,3).contiguous()
        attention = attention.reshape(batch_size, -1, self.d_models)
        output = self.FCLayer(attention)
        return output

掩码： 管理不同的序列长度

上面的代码指的是一个掩码，它允许注意力网络忽略（或不关注）序列中的某些值。一般来说，在时间序列数据中，输入（历史数据窗口）和输出的数量总是由网络固定的，但在语言等其他应用中，输入和输出的数量并不固定。在这个根据所需的属性生成分子结构的小型实验中，输出序列将根据分子的大小和复杂程度而变化；填充掩码通过获取序列并为序列添加填充来帮助处理这种序列长度的变化，从而使所有序列都具有所需的相同长度。例如，考虑到甲烷（“C”）和乙醇（“CCO”）的 SMILES 符号，如果我们定义序列长度为 6，那么这两种分子的填充掩码可以是

甲烷：[1, 0, 0, 0, 0, 0］

乙醇：[1, 1, 1, 0, 0, 0］

其中 0 表示填充，1 表示分子定义字符。掩码与一个大负数相乘（请查看代码），从而产生一个大的负注意力分数。相应的注意力权重基本上为 0，因此，填充掩码有助于网络只关注分子而不关注填充。

我在前面提到过训练 RNN（以及任何变体）的计算挑战，而转换器没有同样的限制，因为在训练过程中，我们可以借助前瞻掩码同时预测整个输出序列。该掩码用于防止模型访问序列中的未来标记，确保只根据过去和现在的标记来预测序列中的每个标记。掩码是一个下三角矩阵：

[[1, 0, 0, 0, 0],
 [1, 1, 0, 0, 0],
 [1, 1, 1, 0, 0],
 [1, 1, 1, 1, 0],
 [1, 1, 1, 1, 1]]

输出序列中的每个元素/标记都是在屏蔽了未来标记的情况下预测的（因此是下三角矩阵）。这只适用于我们可以访问目标输出序列的训练阶段，而不适用于每个标记一次生成一个的推理阶段。

整个架构

在这个小型实验中，我想利用分子特性来预测潜在分子。这些属性包括极性表面积（polararea）、分子复杂性（complexity）、重原子数（heavycnt）、氢键供体（hbonddonor）和氢键受体（hbondacc）。实际上，我是根据现有数据来选择这些属性的，但只要所选属性能够很好地反映相应的分子结构，那么该模型就可以与任何属性集配合使用。

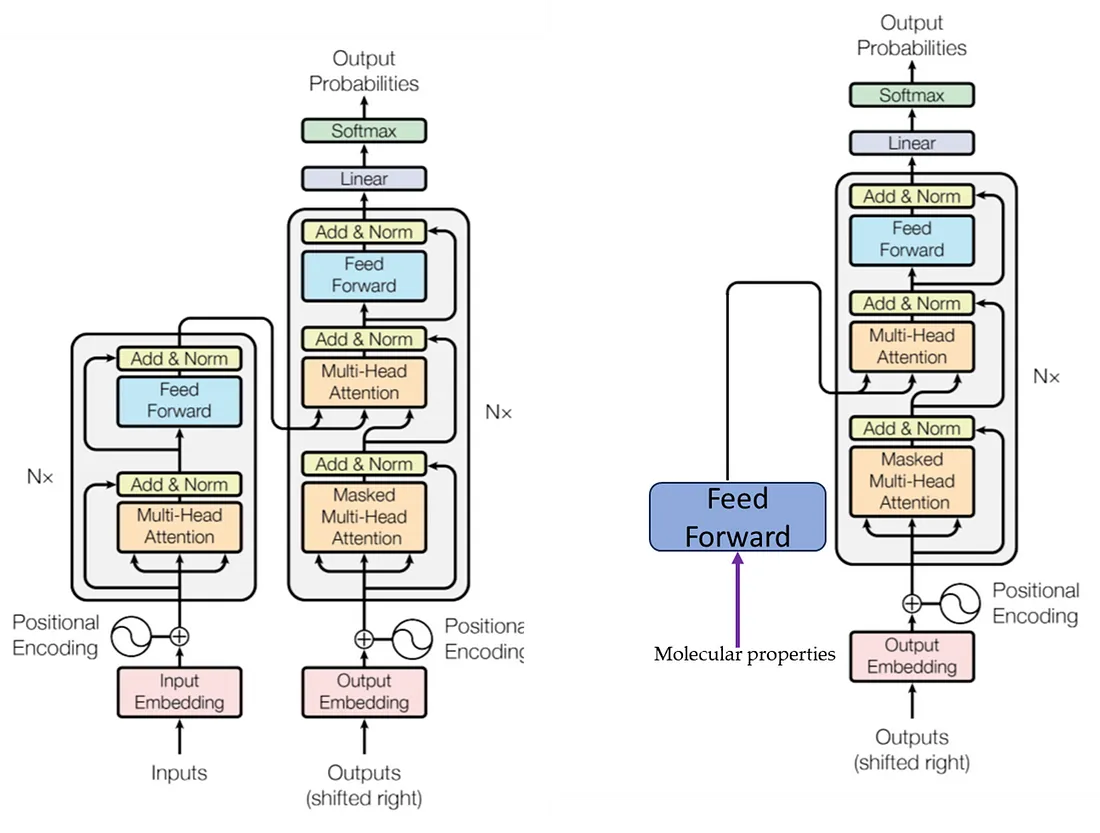
由于这些分子特性输入并不是一个序列，因此传统的变压器网络编码器已经失效，可以用一个简单的 ANN 前馈网络来代替。解码器使用分子的 SMILEs 符号，可将其视为序列，因此解码器基本不变。

# THE ENCODER
class EncoderLayer(nn.Module):
    def __init__(self,d_model,dff):
        super(EncoderLayer,self).__init__()
        self.FeedForwardNN = nn.Sequential(
            nn.Linear(d_model,dff),
            nn.ReLU(),
            nn.Linear(dff,dff)
        )
    def forward(self,x):
        output = self.FeedForwardNN(x)
        return output

# THE DECODER LAYER
class DecoderLayer(nn.Module):
    def __init__(self,d_model, num_heads, dff):
        super(DecoderLayer,self).__init__()
        self.MultiHAttention1 = MultiHeadAttention(d_model, num_heads)
        self.MultiHAttention2 = MultiHeadAttention(d_model, num_heads)
        self.FeedForwardNN = nn.Sequential(
            nn.Linear(d_model,dff),
            nn.ReLU(),
            nn.Linear(dff,d_model)
        )
        self.layerNorm1 = nn.LayerNorm(d_model, eps=1e-6)
        self.layerNorm2 = nn.LayerNorm(d_model, eps=1e-6)
        self.layerNorm3 = nn.LayerNorm(d_model, eps=1e-6)
    def forward(self, x, enc_output, look_ahead_mask, padding_mask):
        attn_output1 = self.MultiHAttention1(x,x,x,look_ahead_mask)
        attn_output1 = self.layerNorm1(x+attn_output1)
        attn_output2 = self.MultiHAttention2(enc_output, enc_output,attn_output1, padding_mask)
        attn_output2 = self.layerNorm2(attn_output2+attn_output1)
        Feedforward_output = self.FeedForwardNN(attn_output2)
        final_output = self.layerNorm3(attn_output2+Feedforward_output)
        return final_output

解码器层采用与插图中相同的结构，有两个多头注意层，中间是前馈层和归一化层。这代表了解码器的单次通过，但实际上序列要通过该网络进行多次迭代改进。完整的解码器组合如下；除了通过解码器层的迭代细化外，还有两个关键要素值得讨论。

首先，目标序列被用作解码器的输入，并被转换为嵌入，在这里我们使用的是随机嵌入向量，这对于准确性来说并不理想，有必要更加谨慎，但对于实验和演示目的来说，这是没有问题的。

class Decoder(nn.Module):
    def __init__(self, num_layers, d_model, num_heads, dff, target_vocab_size, maximum_position_encoding):
        super(Decoder, self).__init__()
        self.d_model = d_model
        self.num_layers = num_layers
        self.embedding = nn.Embedding(target_vocab_size, d_model) # d_model is the size of embedding vector
        self.pos_encoding = self.positional_encoding(maximum_position_encoding, d_model)
        self.dec_layers = nn.ModuleList([DecoderLayer(d_model, num_heads, dff) for _ in range(num_layers)])
    def positional_encoding(self, position, d_model):
        angle_rads = self.get_angles(np.arange(position)[:, np.newaxis], np.arange(d_model)[np.newaxis, :], d_model)
        angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
        angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
        pos_encoding = angle_rads[np.newaxis, ...]
        return torch.tensor(pos_encoding, dtype=torch.float32)
    def get_angles(self, pos, i, d_model):
        angle_rates = 1 / np.power(1000, (2 * (i // 2)) / np.float32(d_model))
        return pos * angle_rates
    def forward(self, x, enc_output, look_ahead_mask, padding_mask):
        seq_len = x.size(1)
        x = self.embedding(x)
        x *= torch.sqrt(torch.tensor(self.d_model, dtype=torch.float32))
        x += self.pos_encoding[:, :seq_len, :]
        for i in range(self.num_layers):
            x = self.dec_layers[i](x, enc_output, look_ahead_mask, padding_mask)
        return x

其次，位置编码用于包含序列的顺序信息。如前所述，多头注意力网络会同时考虑序列中所有标记之间的关系，而不管它们的位置如何。这一点很重要，因为它能使模型捕捉到长程依赖关系，但它对所有标记符一视同仁，并不了解标记符在序列中的相对或绝对位置。例如，考虑一个句子，由于自我注意网络不关注序列中的位置，因此对句子进行任何可变的洗牌都不会产生任何影响。但是，序列中标记的顺序是很重要的，如果改变顺序，句子的含义或在本应用中的分子结构就会发生巨大变化。位置编码的计算方法如下：

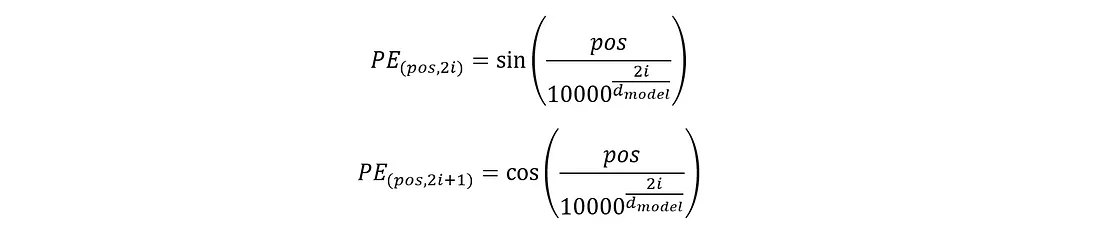
其中，pos 是标记在序列中的位置，i 是嵌入向量中的索引。位置编码的维度应与嵌入矩阵相同。

现在，我们已经完成了整个架构的所有关键部分，我们可以将所有部分组合起来，定义一个转换器模型：

# TRANSFORMER
class Transformer(nn.Module):
    def __init__(self,num_layers, enc_d_model, dec_d_model,
                enc_num_heads, dec_num_heads, enc_dff, 
                dec_dff, target_vocab_size, pe_target):
        super(Transformer, self).__init__()
        self.encoder = EncoderLayer(enc_d_model, enc_dff)
        self.decoder = Decoder(num_layers, dec_d_model, dec_num_heads, dec_dff, target_vocab_size, pe_target)
        self.final_layer = nn.Linear(dec_d_model, target_vocab_size)
    def forward(self, properties, target, look_ahead_mask, dec_padding_mask, training):
        enc_output = self.encoder(properties)
        enc_output_reshaped = enc_output.unsqueeze(1).repeat(1, target.shape[1],1)
        dec_output = self.decoder(target, enc_output_reshaped, look_ahead_mask, dec_padding_mask)
        ffl_output = self.final_layer(dec_output)
        return ffl_output

评估模型

让我们来讨论一下模型的性能。我在大约 5000 个分子上对模型进行了 8 次训练。模型本身几乎没有经过优化，但令人惊讶的是，它做得还不错！让我们看看测试过程中生成分子的一些示例：

Generated SMILES: <start>[O-].[O-].[O-].[O-].[Al+2]<end><start>[O-].[O-].[O-].[O-].[Al+2]<end>
actual smiles: <start>[N-]=[N+]=O<end>
Generated SMILES: <start>C1=C(C(=C(C(=C1Cl)Cl)Cl)C(=O)Cl)Cl)C(=O)Cl<end>
actual smiles: <start>C1[C@@H]2[C@H]3[C@@H]([C@H]1[C@H]4[C@@H]2O4)[C@]5(C(=C([C@@]3(C5(Cl)Cl)Cl)Cl)Cl)Cl<end>
Generated SMILES: <start>CC1=CC(=C(C=C1)C(=O)OC2=CC=CC=C2)C<end>
actual smiles: <start>CC(C)CC(=O)O[C@@H]1CC2CC[C@]1(C2(C)C)C<end>
Generated SMILES: <start>[O-]S(=O)(=O)[O-].[Na+]<end>
actual smiles: <start>C(=O)([O-])[O-].[Mg+2]<end>
Generated SMILES: <start>CCCCCCCCCCCCCCO<end>
actual smiles: <start>CN1CCC[C@H]1C2=CN=CC=C2.Cl<end>
Generated SMILES: <start>CCCCCCCCCCCCO<end>
actual smiles: <start>CCCCCCCC1OCC(O1)C<end>
Generated SMILES: <start>CCCCCCCCCCCCCCCC(=O)OC(=O)CCCC(=O)C<end>
actual smiles: <start>CC(C)(C)C1=CC=CC=C1OP(=O)([O-])OC2=CC=CC=C2<end>
Generated SMILES: <start>CC(=O)OC(=O)C1=CC=CC=C1<end>
actual smiles: <start>C1CN1P(=O)(N2CC2)N3CC3<end>
Generated SMILES: <start>CC(=O)OC(=O)OCC<end>
actual smiles: <start>C=O.C=O.C=O.C=O.C=O.[Fe]<end>
Generated SMILES: <start>CCCCCCCCCC<end>
actual smiles: <start>C=CC1=CC=CC=C1Cl<end>
Generated SMILES: <start>CCCCCCCCCCCCCCCCO<end>
actual smiles: <start>CCCCCCCOC(=O)CCCCCC<end>
Generated SMILES: <start>C(C(C(C(C(C(CO)O)O)O)O)O)C(C(C)O)O<end>
actual smiles: <start>C(CNCCNCCNCCNCCN)N<end>
Generated SMILES: <start>CC(C)C(=O)O<end>
actual smiles: <start>CC(C)(C#C)O<end>
Generated SMILES: <start>[NH4+]<end>
actual smiles: <start>[W]<end>
Generated SMILES: <start>[NH4+]<end>
actual smiles: <start>[He]<end>
Generated SMILES: <start>C(C(=O)O)OC(=O)O.C(C(=O)O)O.C(=O)O.[Na+]<end>
actual smiles: <start>C(C(=O)[O-])C(CC(=O)[O-])(C(=O)[O-])O.N.O.[Fe+3]<end>
Generated SMILES: <start>CCCCCCCCCCCCO<end>
actual smiles: <start>CCCCCCCCCC(=O)OC<end>
Generated SMILES: <start>CCCCCCCCCC(=O)OCC<end>
actual smiles: <start>CC/C=C\C/C=C/CCOC(=O)C<end>
Generated SMILES: <start>CCCCC=O<end>
actual smiles: <start>C1=CC=NC=C1<end>
Generated SMILES: <start>CCCCCCCC(=O)O<end>
actual smiles: <start>CC1=CC(=CC=C1)C(=O)O<end>
Generated SMILES: <start>CCCCCCCCCCC<end>
actual smiles: <start>CC(C)(C)C1=CC=CC=C1<end>
Generated SMILES: <start>CC1=CC(=C(C=C1)[N+](=O)[O-])[N+](=O)[O-](Cl)Cl<end>
actual smiles: <start>C[C@]12CC[C@@H](C1(C)C)C[C@@H]2OC(=O)CSC#N<end>
Generated SMILES: <start>CCCCCCCCCC(=O)OCC(=O)O<end>
actual smiles: <start>C=CCOC(=O)C1=CC=CC=C1N<end>
Generated SMILES: <start>CC1=CC(=C(C=C1)C2=CC=CC=C2C(=C2)C(=O)OC(=O)CC(C)C)C(C)C(C)C(C)CC(C)C<end>
actual smiles: <start>C1C(CC2=CC=CC=C2C1C3=C(C4=CC=CC=C4OC3=O)O)C5=CC=C(C=C5)C6=CC=C(C=C6)Br<end>
Generated SMILES: <start>C(C(F)(F)(F)F)(F)F<end>
actual smiles: <start>C(C(F)(Br)Br)(F)(F)F<end>
Generated SMILES: <start>CC(=O)OC(=O)CC(=O)C<end>
actual smiles: <start>COC(=O)/C=C/C(=O)OC<end>
Generated SMILES: <start>CCCCCCCCCC=O<end>
actual smiles: <start>CC1=CC2=CC=CC=C2O1<end>
Generated SMILES: <start>CCCCCCCCCCCCC(=O)OC(=O)CCC<end>
actual smiles: <start>C1=CC(=CC=C1[N+](=O)[O-])OC2=C(C=C(C=C2)Cl)Cl<end>
Generated SMILES: <start>CCCCCCCCCC=O<end>
actual smiles: <start>CCCCC=C(CC)C=O<end>
Generated SMILES: <start>CC(=O)OC(=O)C<end>
actual smiles: <start>COP(=O)(C)OC<end>
Generated SMILES: <start>CC(=O)[O-].CC(=O)[O-].[Na+]<end>
actual smiles: <start>CC(C)SSSC(C)C<end>
Generated SMILES: <start>CCCCC=O<end>
actual smiles: <start>CCSCCCl<end>

为这些模型确定一个合理的评估指标具有挑战性，因为虽然结构相似性可以作为一个指标，但评估生成的分子在多大程度上满足指定的特性才是关键。但这并不容易做到。

首先，该模型甚至能够生成化学上有效的 SMILES 字符串，这给我留下了深刻印象。像 “CCCCCCCCCCCCCCO ”这样的字符串是带有羟基的长碳链，而 “CC(=O)OC(=O)C ”则是简单的酯，代表了有效的分子结构。

然而，在立体化学和复杂结构方面还存在挑战，例如生成的 SMILES “C1=CC=C(C=C1)C(=O)O”（对应苯甲酸）与实际目标分子 “CC(=O)NC1=CC=C(C=C1)Cl ”相比，结构要简单得多。总的来说，该模型似乎遗漏了一些特定的立体化学构型，这表明我们需要更多的训练数据或调整模型，以便捕捉到这些特定的分子结构。

另一个问题似乎是模型倾向于生成更简单的分子，例如，当目标分子有多个手性中心时，模型可能只生成一个更简单的非手性分子。这种过度简化分子的现象很可能是由于模型本身偏向于生成更常见、更简单的结构，而这些结构在训练过程中出现的频率更高。

在没有进一步数据的情况下很难确认的一个潜在问题是，所需的输入分子特性与分子结构的映射程度如何。虽然生成的分子可能与目标分子不匹配，但它可能具有所需的输入属性，这表明模型正在学习生成符合指定属性约束的分子。在这种情况下，限制性能的不是模型，而是需要更多映射到独特分子结构的特征数据。