异常值通常被定义为数据集中与其他大多数项目截然不同的项目。也就是说：任何记录如果与所有其他记录（或几乎所有其他记录）有明显差异，并且与其他记录的差异大于正常值，都可以被合理地视为异常值。

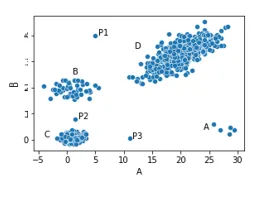
在这里显示的数据集中，我们有四个聚类（A、B、C 和 D）和这些聚类之外的三个点： P1、P2 和 P3。这些点很可能被视为异常值，因为它们都与所有其他点相差甚远，也就是说，它们与大多数其他点都有明显的不同。

此外，A 组只有五个点。虽然这些点之间的距离相当近，但它们与所有其他点的距离都很远，因此也很有可能被视为异常值--同样是基于这些点与大多数其他点之间的距离。

另一方面，离群点（较大群组内的点）都与大量其他点非常接近。例如，簇 C 中间的任何一个点都与许多其他点非常接近（即与许多其他点非常相似），因此不会被视为离群点。

我们还有很多其他方法可以查看异常值，实际上也有很多其他方法用于异常值检测，例如基于常项集、关联规则、压缩、马尔可夫模型等的异常值检测方法。但是，识别与其他记录相似但与最相似记录相对不同的记录是非常常见的。事实上，这也是许多最常见的离群点检测算法背后的基本思想，包括 kNN、LOF（局部离群因子）、Radius 和许多其他算法。

但是，使用这种方法就会留下一个问题，即如何量化一条记录与其他记录的不同程度。有很多技术可以做到这一点。离群点检测中最常见的一些技术包括欧几里得距离、曼哈顿距离和高尔距离，以及一些类似的指标。

我们将在下面快速介绍这些方法。但我们想在这篇文章中专门介绍一种非常通用，但可能使用不足的方法，即计算表格数据中两条记录之间的差值，这种方法对离群点检测非常有用，称为距离度量学习，以及将其专门应用于离群点检测的方法。

距离度量

要确定一条记录是否：1）与其他大多数记录的距离异常遥远；2）与相对较少的记录距离较近，我们通常首先计算成对距离：数据集中每对记录之间的距离。在实践中，我们可能会采取更优化的方法（例如，在已知记录之间的距离非常远的情况下，只计算近似距离），但至少在原则上，计算每对记录之间的距离在离群点检测中很常见。

也就是说，我们需要一种方法来计算任意两条记录之间的距离。

如果我们有一组数据，比如下面这个员工记录大表（这里显示的是随机的四行子集），如何才能最好地说明任何两行的相似程度？

欧氏距离

一种非常常用的方法是使用欧氏距离。

在进一步研究员工数据之前，请再看一下上面的散点图。在这里，我们可以看到使用欧氏距离的自然效果。由于这个数据集只包含两个特征，而且都是数字特征，因此像图中那样绘制数据（散点图）是相当直观的。而且，一旦以这种方式绘制，我们就会很自然地描绘出点与点之间的欧氏距离（基于勾股定理公式）。

但是，如果有许多特征，其中许多特征是分类的，而且列之间存在关联，那么行与行之间的欧氏距离虽然仍然有效，而且通常也很有用，但感觉就不那么自然了

欧氏距离的一个问题是，它实际上是为数值数据设计的，而现实世界中的大多数数据，如员工记录，都是混合数据：既包含数值特征，也包含分类特征。分类值可以进行数字编码（例如，使用 One-Hot、Ordinal 或其他编码方法），这样就可以计算欧氏距离（以及其他数字距离度量）。但这种方法并不总是理想的。每种数字编码方法对计算的距离都有自己的影响。但这是完全可能的，而且很常见。

以上面的员工表为例：在离群点检测过程中，我们可能会忽略身份证和姓氏，而使用其余的列。鉴于此，我们仍将部门和办公室特征作为分类特征。假设我们使用单次编码对其进行编码。

为了计算行间的欧氏距离，我们还必须对数字特征进行缩放，将所有特征放在同一比例尺上。这有多种方法，包括标准化（根据数值与该列平均值的标准差数，将数值转换为 Z 值）或最小-最大缩放。

对数据进行数字编码和缩放后，我们就可以计算每对行之间的欧氏距离了。

高尔距离

另外，鉴于我们有一些分类特征，我们可以使用一种专为混合数据设计的方法，例如高尔距离。这种方法在比较任意两行时，会逐列计算差值，并将这些差值相加。如果数据是严格的数字数据，它相当于曼哈顿距离。

对于分类列，使用高尔距离时通常使用序数编码，因为我们只关心是否有完全匹配的数据。分类列中两个值的差值为 0.0 或 1.0。在上面的员工表中，Smith 和 Jones 所在部门的距离为 1.0（1.0 通常用于不同的值： 在本例中，“工程 ”和 “销售 ”的距离为 1.0），而 “办公室 ”的距离为 0.0（如果两行的值相同，则始终使用 0.0：在本例中为 “多伦多”）。

要对数值字段进行比较，就像欧氏和大多数距离度量一样，我们需要先对它们进行缩放，以便对所有数值字段一视同仁。如前所述，有多种方法可以做到这一点，但让我们假设在这里使用最小-最大缩放，将所有数值置于 0.0 和 1.0 之间。这样，我们就可以得到这样一个表格，例如：

这样，史密斯和琼斯的差值（使用Gower距离）就是：abs(0.90 - 0.20) + abs(0.93 - 0.34) + abs(0.74 - 0.78) + 1.0 + abs(0.88 - 0.77) + abs(0.54 - 0.49) + 0.0 + abs(0.32 - 0.38)。

也就是说，跳过身份证和姓氏，我们计算每个数字字段的绝对差值，并在每个分类字段中取 0.0 或 1.0。

这可能是合理的，但也存在一些问题。主要问题可能是分类字段的权重高于数值字段：分类字段的差值通常为 1.0，而数值字段的差值往往较小。例如，Smith 和 Jones 之间的年龄差异很大，但差异值只有 abs(0.93-0.34)，即 0.59（仍然很显著，但小于部门计入行间总差异的 1.0）。正如《Python 中的离群点检测》一书中所述，单次编码和使用其他距离度量的其他编码在处理混合数据时也有类似的问题。

此外，所有分类特征之间的相关性都是相同的；所有数字特征之间的相关性也是相同的，即使有些特征是高度相关的，或者在其他方面应该具有更高或更低的权重。

一般来说，欧氏或高尔距离等距离度量（以及曼哈顿、堪培拉等其他度量）在很多情况下都是合适的距离度量，通常也是离群点检测的绝佳选择。但与此同时，它们并不总是所有项目的理想选择。

将欧氏距离视为高维空间中的物理距离

再看欧氏距离，这些距离本质上是将每条记录视为高维空间中的点，并计算这些点在该空间中的距离。曼哈顿距离和高尔距离略有不同，但工作原理十分相似。

作为比整个员工表更简单的示例，请看这个表，但目前只包括数字特征： 服务年限、年龄、薪水、假期天数、病假天数和最后一次奖金。这就是六个特征，因此每一行都可以看作是六维空间中的一个点，它们之间的距离用勾股定理公式计算。

这种方法是合理的，但肯定不是查看距离的唯一方法。而且，所使用的距离度量会对离群点的评分产生很大的影响。例如，与曼哈顿距离相比，欧几里得距离会更重视一些数值差异很大的特征。

欧氏距离和曼哈顿距离示例

在此，我们将考虑这种 6 维数据的两种不同情况（同时显示 ID 和姓氏列以供参考）。

首先，以 Greene 和 Thomas 这两位员工为例，他们的大部分数值都很相似，但服务年限却大相径庭：

其次，以福特和李这两位职员为例，这两位职员的大多数价值观差异不大，但都不太一样：

这两行中哪一行最相似？使用曼哈顿距离，格林和托马斯最相似（距离为 0.59，而托马斯为 0.60）。如果使用欧氏距离，福特和李最相似（距离为 0.27，而李为 0.50）。

使用曼哈顿距离或欧氏距离更合适，或者使用其他度量，如堪培拉距离、闵科夫斯基距离（例如使用立方距离）、马哈拉诺比斯距离等更合适，这一点并不总是很清楚。这并不一定是个问题，但它确实强调了有很多方法可以查看行间距离。

具体来说，欧几里得距离意味着我们将数据视为高维空间中的点，并计算它们之间的物理距离。这有一定的实际价值，但并不总是完全自然的。只要看一下数值表，比如上面的员工数据，我们就会把行（在这个例子中）想象成员工记录，而不是空间中的点。

而且，使用欧氏距离需要计算年龄平方、工资平方等，这缺乏直观的吸引力。例如，年龄平方的真正含义并不清楚。它可以很好地工作，但对数据的几何解释实际上只是我们描绘数据的众多方法之一。

此外，这是一种通用方法，并不考虑数据本身。

距离度量学习

距离度量学习提出了另一种思考问题的方法，即确定两条记录的相似程度。距离度量学习法不是先定义一个距离度量，然后将其应用于手头的数据，而是试图从数据本身了解记录之间的相似程度。

它还解决了欧几里得、曼哈顿和大多数其他距离度量的一个局限性：即所有特征都一视同仁，无论这是否最合适。

这里的想法是：有些特征比其他特征更相关，有些特征彼此相关（在某些情况下，特征集甚至可能是多余的，或者几乎是多余的）。简单地对每个特征进行相同处理并不一定是识别数据集中最异常记录的最佳方法。

距离度量学习（Distance Metric Learning）本身就是一个重要的领域，但在这里我将介绍一种将其应用于离群点检测的方法。具体来说，我们将在此探讨基于创建随机森林的离群点检测中的距离度量学习应用。

假设：

1. 我们有一个能预测某个目标的随机森林
2. 我们有一个可以通过随机森林的数据表（例如员工数据，但也可以是任何表格数据）
3. 我们要计算每对行之间的距离。

在这里，我们将使用这些成对距离进行离群点检测，但原则上也可以用于任何目的。

我们很快就会介绍如何为此创建随机森林，但现在先假设我们已经有了一个随机森林，而且它质量上乘、训练有素、稳健可靠。

我们可以通过观察随机森林所做的预测来估算行与行之间的相似度。假设随机森林训练成了二元分类器，因此可以为数据中的每条记录预测出成为正类的概率。

通过随机森林的两条记录可能有非常相似的概率，比如 0.615 和 0.619。这两个概率非常接近，因此我们可以怀疑这两条记录彼此相似。但也不一定。实际上，在随机森林的众多决策树中，它们可能会遵循完全不同的决策路径，并碰巧得出相似的平均预测结果。也就是说，它们可能因为不同的原因得到相似的预测结果，也可能根本不相似。

最重要的是记录在决策树中的决策路径。如果两条记录在决策树中的大部分路径相同（因此在相同的叶节点中结束），那么我们就可以说它们是相似的（至少在这方面）。而如果它们在大部分情况下都以不同的叶节点为终点，我们就可以说它们是不同的。

这就为我们提供了一个强大的工具，以合理的方式确定任何两条记录的相似程度。

创建随机森林

这显然是一个有用的想法，但它确实需要一个随机森林，一个对这一目的有意义的随机森林--一个能很好地捕捉可用数据性质的随机森林。

创建这样一个随机森林的方法之一，就是建立一个能学会将这些数据与类似但虚假的数据区分开来的随机森林。也就是说，人工合成的数据与这些数据相似，但又不完全相同（因此无法区分）。

因此，如果我们能创建这样一组虚假数据，就可以训练随机森林分类器来区分这两类数据。

创建合成数据的方法有很多，其中包括《Python 中的离群点检测》一书中介绍的几种方法。例如，其中一种方法是使用兴奋剂。不过，我们将在此探讨另一种效果不错的方法。这种方法可能过于简单，而且并不总是像更复杂的技术那样有效，但它确实是对这一想法的一个很好的简单介绍。

在这里，我们生成的合成记录数量与真实记录数量相等。我们并不需要一个完全平衡的数据集，在某些情况下，一些不平衡的数据集可能效果更好，但为了简单起见，本示例使用了一个平衡的数据集。

我们每次生成一行合成数据，每行生成一个特征。要生成一个值，如果特征是分类的，我们就从真实数据中选择一个值，其概率与真实数据的分布成正比。例如，如果真实数据包含一列 “颜色”，其中红色行 450 行，蓝色行 650 行，绿色行 110 行，黄色行 385 行： 红色：0.28，蓝色：0.41，绿色：0.07，黄色：0.41： 0.07，黄色 0.24. 我们将在合成数据中为这一列创建一组比例相似的新值。

如果特征是数值型的，我们会计算该特征的真实数据的平均值和标准偏差，然后从具有这些参数的正态分布中选择一组随机值。我们还可以考虑其他方法，但这只是对这一想法的简单介绍。

这样，我们就生成了合成数据，其中每一行都完全由现实值组成（每一行都有可能包含分类列中的罕见值，以及数值列中的罕见值或极端值，但它们都是合理的现实值）。

但是，特征之间的正常关系并没有得到尊重。也就是说：由于每一列的值都是独立生成的，因此生成的值组合可能不符合实际情况。例如，如果创建合成数据来模仿上面的员工表，我们可能会创建年龄为 23 岁、服务年限为 38 年的虚假记录。这两个值本身都符合实际情况，但组合起来就不合理了，因此在真实数据中应该是不可见的组合--这样才能与真实数据区分开来。

数字字段的合成数据可以用代码（python）创建，例如

real_df['Real'] = True
synth_df = pd.DataFrame() 
for col_name in real_df.columns:
    mean = real_df[col_name].mean()
    stddev = real_df[col_name].std()
    synth_df[col_name] = np.random.normal(
       loc=mean, scale=stddev, size=len(real_df))
synth_df['Real'] = False
train_df = pd.concat([real_df, synth_df])

在这里，我们假设数据帧 real_df 包含真实数据。然后，我们创建第二个名为 synth_df 的数据帧，再将两者合并为 train_df，用于训练随机森林来区分两者。

分类数据的创建方法与此类似：

for col_name in real_df.columns:    .columns:    
    vc = real_df[col_name].value_counts(normalize=True)
    synth_df[col_name] = np.random.choice(a=vc.keys().tolist(), 
                                          size=len(real_df),
                                          replace=True, 
                                          p=vc.values.tolist())

如上所述，这只是生成数据的一种方法，对这一过程进行调整，允许更多不寻常的单一值，或限制特征间不太寻常的关系，可能会有所帮助。

一旦创建了这些数据，我们就可以训练随机森林来学习区分真假数据。

一旦这样做了，我们实际上也可以执行另一种形式的离群点检测。任何通过随机森林预测为假记录的真实记录都可能被视为异常数据--它们与合成数据的相似度高于真实数据。在本文中，我们将重点关注距离度量学习，因此要查看的是随机森林中通过树的决策路径（而不是最终预测结果）。

使用随机森林测量离群程度

如上所述，如果两条记录倾向于以几乎完全不同的叶节点结束，那么至少在这个意义上，它们可以被认为是不同的。

我们可以针对每对记录，计算随机森林中它们以相同叶节点结束和以不同叶节点结束的树的数量。不过，我们还可以使用一种更简单的方法。对于通过随机森林的每条记录，我们可以查看每棵树的终端（叶子）节点是什么。我们还可以查看训练数据中有多少记录以该节点为终点。训练记录越少，这条路径就越不寻常。

如果在大多数树中，某条记录与其他极少数记录一样，都以相同的叶节点为终点，那么这条记录就可以被视为异常记录。

如果随机森林只包含少量的树，那么每条记录的叶节点的大小可以非常随意。但是，随机森林可以设置成拥有成百上千棵树。如果记录总是以不寻常的树叶节点结束，就可以合理地认为该记录异常。

即使使用的是大型随机森林，处理过程中仍可能存在一些差异。为了解决这个问题，我们可以不使用单一的距离度量学习离群点检测器，而是使用多个离群点检测器进行组合。这超出了本文的讨论范围，但总体思路是创建各种合成数据集，并为每个数据集创建各种随机森林（采用不同的超参数），然后将结果平均到一起。

示例

为了演示这个想法，我们将创建一个简单的距离度量学习检测器。

但首先，我们要创建几个测试数据集。这两个数据集都是有两个特征的数字数据集。如前所述，这比具有许多特征和许多分类特征的数据更不真实，但它对演示目的很有用--它易于绘制和理解。

第一个测试集是一个单一的数据集群：

import numpy as np
import pandas as pd
def create_simple_testdata():
    np.random.seed(0)
    a_data = np.random.normal(size=100)
    b_data = np.random.normal(size=100)
    df = pd.DataFrame({"A": a_data, "B": b_data})
    return df

第二种方法实际上是创建文章开头所示的数据集，其中有四个聚类和三个聚类之外的点。

def create_four_clusters_test_data():
    np.random.seed(0)
    a_data = np.random.normal(loc=25.0, scale=2.0, size=5) 
    b_data = np.random.normal(loc=4.0, scale=2.0, size=5)
    df0 = pd.DataFrame({"A": a_data, "B": b_data})
    a_data = np.random.normal(loc=1.0, scale=2.0, size=50) 
    b_data = np.random.normal(loc=19.0, scale=2.0, size=50)
    df1 = pd.DataFrame({"A": a_data, "B": b_data})
    a_data = np.random.normal(loc=1.0, scale=1.0, size=200) 
    b_data = np.random.normal(loc=1.0, scale=1.0, size=200)
    df2 = pd.DataFrame({"A": a_data, "B": b_data})
    a_data = np.random.normal(loc=20.0, scale=3.0, size=500) 
    b_data = np.random.normal(loc=13.0, scale=3.0, size=500) + a_data
    df3 = pd.DataFrame({"A": a_data, "B": b_data})
    outliers = [[5.0, 40], 
                [1.5, 8.0],
                [11.0, 0.5]]
    df4 = pd.DataFrame(outliers, columns=['A', 'B'])
    df = pd.concat([df0, df1, df2, df3, df4])
    df = df.reset_index(drop=True)
    return df

这两个数据集在此显示：

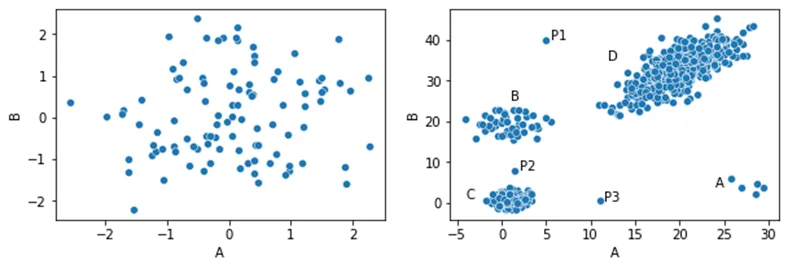
接下来，我们将展示一个基于距离度量学习的简单异常值检测器。该检测器的 fit_predict()方法通过一个数据帧（我们在其中识别任何异常值）。fit_predict()方法生成一个合成数据集，训练随机森林，通过随机森林传递每条记录，确定每条记录以哪个节点结束，并确定这些节点的常见程度。

from sklearn.ensemble import RandomForestClassifier
from collections import Counter
from sklearn.preprocessing import RobustScaler
class DMLOutlierDetection:
    def __init__(self):
        pass
    def fit_predict(self, df):
        real_df = df.copy()
        real_df['Real'] = True
        # Generate synthetic data that is similar to the real data
        # For simplicity, this covers just the numeric case.  
        synth_df = pd.DataFrame() 
        for col_name in df.columns:
            mean = df[col_name].mean()
            stddev = df[col_name].std()
            synth_df[col_name] = np.random.normal(loc=mean, 
               scale=stddev, size=len(df))
        synth_df['Real'] = False
        train_df = pd.concat([real_df, synth_df])
        clf = RandomForestClassifier(max_depth=5)
        clf.fit(train_df.drop(columns=['Real']), train_df['Real'])
        # Get the leaf node each record ends in 
        r = clf.apply(df) 
        # Initialize the score for all records to 0
        scores = [0]*len(df) 
        # Loop through each tree in the Random Forest
        for tree_idx in range(len(r[0])): 
            # Get the count of each leaf node
            c = Counter(r[:, tree_idx]) 
            
            # Loop through each record and update its score based 
            # on the frequency of the node it ends in
            for record_idx in range(len(df)): 
                node_idx = r[record_idx, tree_idx]
                node_count = c[node_idx]
                scores[record_idx] += len(df) - node_count
        return scores
df = create_four_clusters_test_data()
df = pd.DataFrame(RobustScaler().fit_transform(df), columns=df.columns)
clf = DMLOutlierDetection()
df['Scores'] = clf.fit_predict(df)

本代码示例仅在 create_four_clusters_test_data() 创建的数据上运行，但也可以调用 create_simple_testdata() 创建的数据。

结果可以通过以下代码直观地显示出来：

import matplotlib.pyplot as plt
import seaborn as sns
sns.scatterplot(x=df["A"], y=df['B'], hue=df['Scores'])
plt.show()

两个测试数据集的结果如下所示，绘制的是原始数据，但根据离群点得分（通过上面的代码放在 “得分 ”栏中）设置了色调。

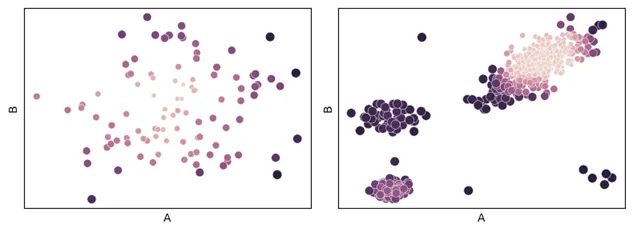
左边的数据集只有一个聚类，最外围的点得分最高，这是意料之中的。右边的数据集有四个聚类，聚类外的三个点、较小的聚类和最大聚类边缘的点得到的离群点分数最高。这是非常合理的，尽管其他检测器可能会对这些点进行不同的评分，而且很可能也是非常合理的。

如上所述，对于这些数据集来说，使用欧氏距离是很自然的，但对于具有许多特征、分类特征、特征之间的关联以及数据的其他细微差别的数据集来说，可能就不那么自然了。但是，即使在这些欧氏公因子效果较好的简单情况下，距离公因子学习也能很好地发挥作用，并提供一种自然的离群点检测方法。在处理更复杂的数据时，情况更是如此。

结论

除离群点检测外，距离公因子学习法还可用于许多其他用途，甚至在离群点检测中也有多种用途。例如，可以使用上述的随机森林来计算数据集中的成对距离，并将其传递给另一种算法。例如，DBSCAN 提供了一个 “预计算 ”选项，允许传递一个预先计算好的成对距离矩阵；然后就可以将 DBSCAN（或类似的聚类方法，如 HDBSCAN）用于几种可能的基于聚类的离群点检测算法之一。

而且，距离度量学习也可以像本文中这样以一种更直接的方式使用，它本身就是一种出色的异常值检测方法。在很多情况下，它比基于欧氏、曼哈顿、高尔或其他此类距离度量的方法更有利于检测异常值。它还能为一组检测器提供多样性，即使这些方法也能很好地发挥作用。

没有一种离群点检测方法是绝对的，通常需要在任何给定的项目中使用多种离群点检测方法（包括经常多次使用相同的方法，使用不同的参数），结合它们的结果来实现强大的整体离群点检测。

因此，距离度量学习法并不是对每个项目都有效，而且当它与其他检测方法结合使用时，效果可能会更好（与其他检测方法一样）。但是，这是一个很有价值的工具；距离公因子学习可以成为一种非常有效的离群点检测技术，尽管它受到的关注比其他方法要少。

它确实需要一些调整，包括合成数据的生成方式和随机森林使用的超参数，但一旦调整好，它就能提供一种强大而直观的离群点检测方法。