先决条件

• 需要掌握 Python 和 Pytorch 的基本知识。
• 对自关注等变换器概念和深度神经网络知识的基本了解当然会有所帮助，但并非必须。

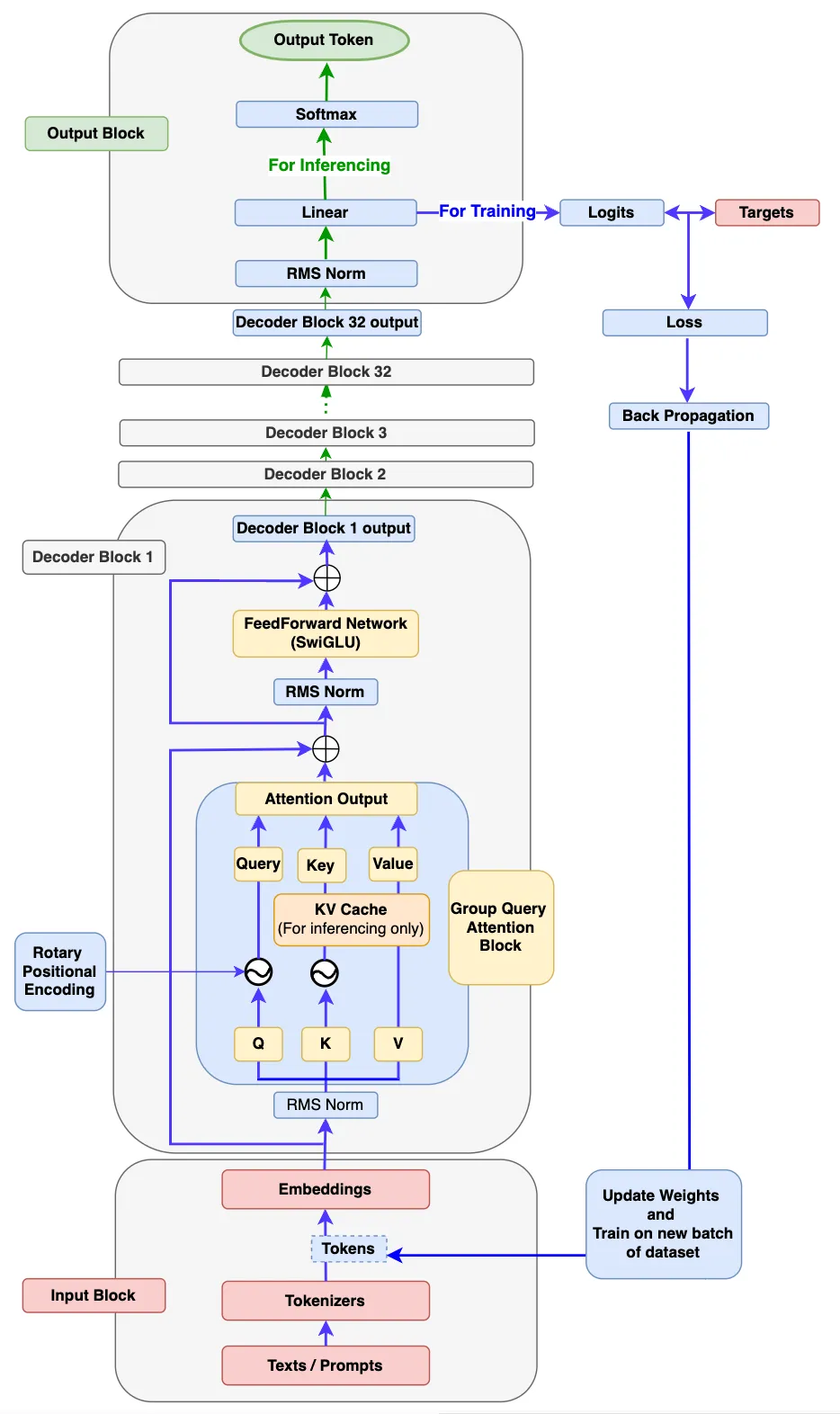
第一步：输入模块

如上图 Llama 3 架构图所示，输入块有 3 个组件：文本/提示、标记器和嵌入。

输入块内部的组件是如何工作的？俗话说 “一图胜千言”，让我们看看下面的流程图，了解输入块内部的工作流程。

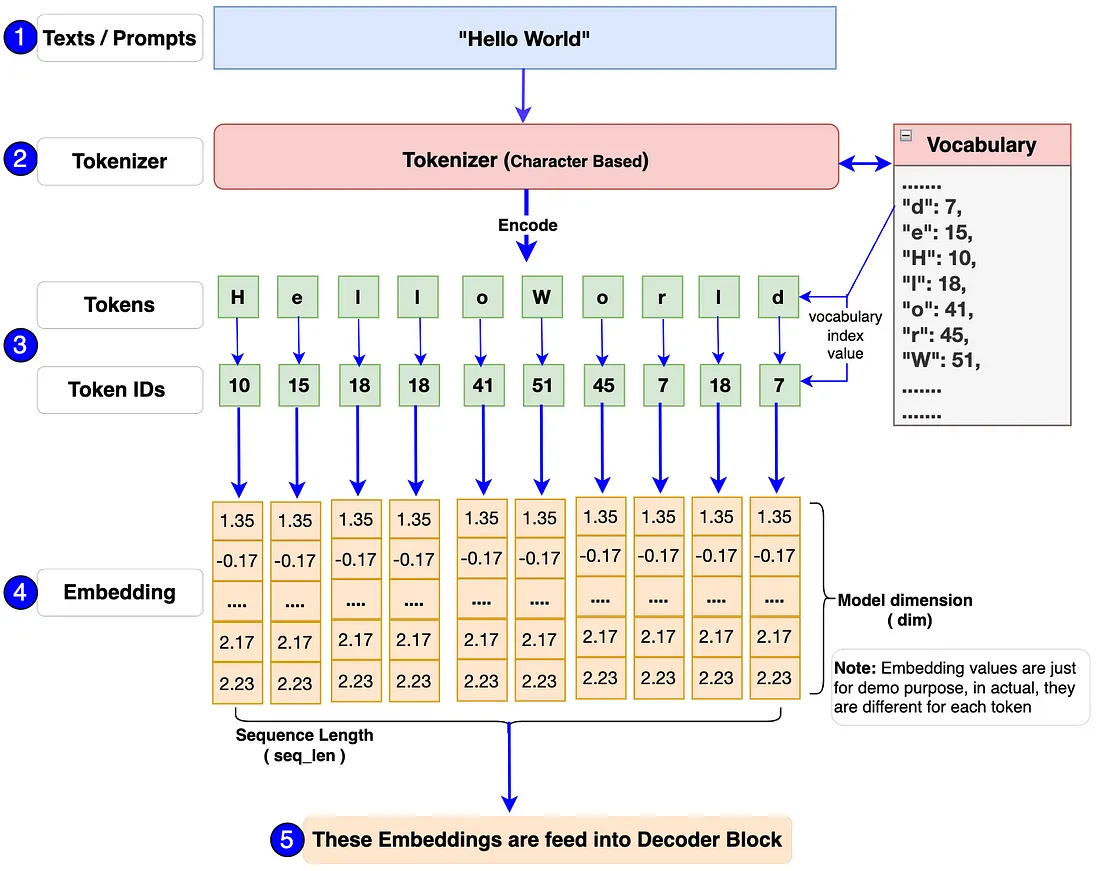
• 首先，一个或一批文本/摘要将被传入模型。例如 如上流程图中的 “Hello World”。
• 由于模型无法处理文本，因此输入模型的内容应始终为数字格式。Tokenizer 可以帮助将这些文本/词条转换为 token-ids（即词汇表中词条的索引号表示法）。我们将使用流行的 Tiny Shakespeare 数据集来建立词汇表并训练我们的模型。
• Llama 3 模型中使用的标记符是 TikToken，这是一种子词标记符。不过，我们将使用字符级标记符来构建模型。主要原因是我们应该知道如何自己构建词汇表和标记符，包括编码和解码函数。这样，我们就能了解引擎盖下的所有工作原理，并完全控制代码。
• 最后，每个 token-id 都将被转换成 128 维的嵌入向量（在最初的 Llama 3 8B 中为 4096）。然后，嵌入向量将进入下一个称为解码器块的程序块。

让我们对输入块进行编码：

# Import necessary libraries
import torch
from torch import nn
from torch.nn import functional as F
import math
import numpy as np
import time
from dataclasses import dataclass
from typing import Optional, Tuple, List
import pandas as pd
from matplotlib import pyplot as plt

### Step 1: Input Block ###
# Using Tiny Shakespeare dataset for character-level tokenizer. Some part of the following character-level tokenizer is referenced from Andrej karpathy's GitHub (https://github.com/karpathy/nanoGPT/blob/master/data/shakespeare_char/prepare.py) which I found is explained very well.
# Load tiny_shakespeare data file (https://github.com/tamangmilan/llama3/blob/main/tiny_shakespeare.txt)
device: str = 'cuda' if torch.cuda.is_available() else 'cpu'   # Assign device to cuda or cpu based on availability
# Load tiny_shakespeare data file.
with open('tiny_shakespeare.txt', 'r') as f:
  data = f.read()
# Prepare vocabulary by taking all the unique characters from the tiny_shakespeare data
vocab = sorted(list(set(data)))
# Training Llama 3 model requires addtional tokens such as <|begin_of_text|>, <|end_of_text|> and <|pad_id|>, we'll add them into vocabulary
vocab.extend(['<|begin_of_text|>','<|end_of_text|>','<|pad_id|>'])
vocab_size = len(vocab)
# Create a mapping between characters with corresponding integer indexes in vocabulary.
# This is important to build tokenizers encode and decode functions.
itos = {i:ch for i, ch in enumerate(vocab)}
stoi = {ch:i for i, ch in enumerate(vocab)}
# Tokenizers encode function: take a string, output a list of integers
def encode(s):
  return [stoi[ch] for ch in s]
# Tokenizers decode function: take a list of integers, output a string
def decode(l):
  return ''.join(itos[i] for i in l)
# Define tensor token variable to be used later during model training
token_bos = torch.tensor([stoi['<|begin_of_text|>']], dtype=torch.int, device=device)
token_eos = torch.tensor([stoi['<|end_of_text|>']], dtype=torch.int, device=device)
token_pad = torch.tensor([stoi['<|pad_id|>']], dtype=torch.int, device=device)
prompts = "Hello World"
encoded_tokens = encode(prompts)
decoded_text = decode(encoded_tokens)
### Test: Input Block Code ###
# You need take out the triple quotes below to perform testing
"""
print(f"Lenth of shakespeare in character: {len(data)}")
print(f"The vocabulary looks like this: {''.join(vocab)}\n")
print(f"Vocab size: {vocab_size}")
print(f"encoded_tokens: {encoded_tokens}")
print(f"decoded_text: {decoded_text}")
"""
### Test Results: ###
"""
Lenth of shakespeare in character: 1115394
The vocabulary looks like this: 
 !$&',-.3:;?ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz<|begin_of_text|><|end_of_text|><|pad_id|>
Vocab size: 68
encoded_tokens: [20, 43, 50, 50, 53, 1, 35, 53, 56, 50, 42]
decoded_text: Hello World
"""

第二步：解码器模块

请看上面的结构图，解码器模块由以下子组件组成。

• 有效值规范
• 旋转位置编码
• KV 缓存
• 组查询注意
• 前馈网络
• 解码器块

2a.RMS Norm（均方根归一化）：

为什么需要 RMSNorm？在上面的结构图中，你一定注意到了输入模块的输出，即嵌入向量会经过 RMSNorm 模块。这是因为嵌入向量有很多维度（在 Llama3-8b 中为 4096 维），而且总有可能出现不同范围的值。这可能导致模型梯度爆炸或消失，从而导致收敛缓慢甚至发散。RMSNorm 可以将这些值纳入一定范围，从而有助于稳定和加速训练过程。这使得梯度的大小更加一致，从而使模型收敛得更快。

RMSNorm 如何工作？让我们先看看下图。

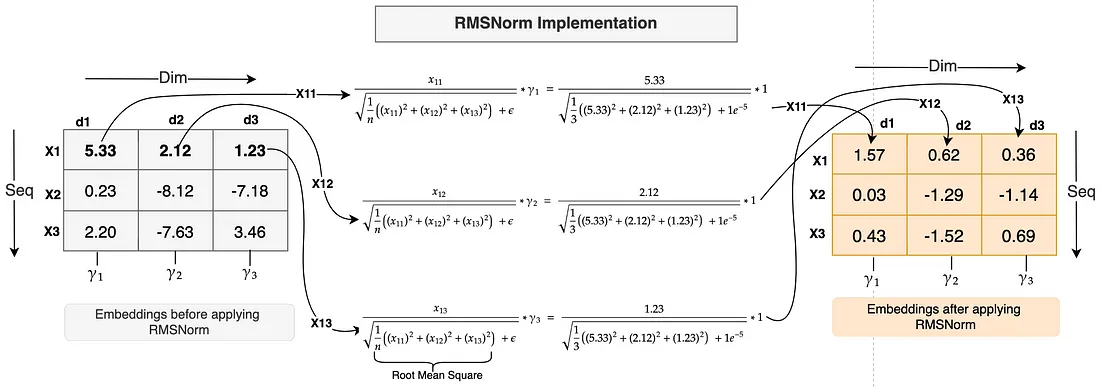
• 与层归一化一样，RMSNorm 也是沿着嵌入特征或维度应用的。上图的嵌入形状为 [3,3]，即每个标记有 3 个维度。

举例说明： 让我们对第一个标记 X1 的嵌入应用 RMSNorm：

• 标记 X1 在每个维度（即 x11、x12 和 x13）上的值将分别除以所有这些值的均方根。计算公式如上图所示。
• E（ε）是一个小常数，被添加到均方根中，以避免被零除以数值的稳定性。
• 最后，再乘以一个比例参数 Gamma (Y)。每个特征都有一个独特的伽马参数（就像上图中的 Y1 表示 dim d1，Y2 表示 dim d2，Y3 表示 dim d3），它是一个学习参数，可以放大或缩小，从而进一步提高归一化的稳定性。gamma参数的初始值为 1（如上图所示）。
• 正如你在上例中所注意到的，嵌入值很大，分布范围很广。应用 RMSNorm 后，嵌入值会小很多，范围也很小。计算是通过实际的 RMSNorm 函数完成的。

为什么选择 RMSNorm 而不是图层归一化？正如你在上面的示例中注意到的，我们没有计算任何平均值或方差，而这在层归一化中是要做的。因此，我们可以说，RMSNorm 避免了平均值和方差的计算，从而减少了计算开销。

让我们对 RMSNorm 进行编码：

# Step2: The Decoder Block
# Note: Since the Llama 3 model is developed by Meta, so to be in sync with their codebase and for future compatibility,
# I will use most of the code from Meta GitHub with some necessary changes required to achieve our goal.
# Define parameters dataclass: we'll use these parameters during model building, training and inference.
# Note: Since we want to see the results of training and inferencing faster rather than focusing on high accuracy, we're taking lower values for most of the parameters which are set higher in the Llama 3 model.
@dataclass
class ModelArgs:
    dim: int = 512              # embedding dimension
    n_layers: int = 8           # number of model decoder blocks
    n_heads: int = 8            # number of heads for queries embedding
    n_kv_heads: int = 4         # number of heads for keys and values embedding
    vocab_size: int = len(vocab) # Length of vocabulary
    multiple_of: int = 256        # Require to calculate dim of feedfoward network
    ffn_dim_multiplier: Optional[float] = None  # Require to calculate dim of feedfoward network
    norm_eps: float = 1e-5                       # Default Epsilon value set for the RMSNorm calculation
    rope_theta: float = 10000.0   # Default theta value for the RePE calculation
    max_batch_size: int = 10     # Max batch size
    max_seq_len: int = 256         # Max sequence length
    epochs: int = 2500             # Total number of training iteration
    log_interval: int = 10        # Number of interval to print the logs and loss values   
    device: str = 'cuda' if torch.cuda.is_available() else 'cpu'   # Assign device to cuda or cpu based on availability 

## Step2a: The RMSNorm
class RMSNorm(nn.Module):
  def __init__(self, dim: int, eps: float = 1e-6):
    super().__init__()
    device = ModelArgs.device
    self.eps = eps
    # Scaling parameter gamma, initialized with one and the no of parameters is equal to the size of dim
    self.weight = nn.Parameter(torch.ones(dim).to(device))
  def _norm(self, x):
    return x * torch.rsqrt(x.pow(2).mean(dim=-1, keepdim=True) + self.eps).to(device)
  def forward(self, x):
    #Shape: x[bs,seq,dim]
    output = self._norm(x.float()).type_as(x)
    #Shape: x[bs,seq,dim] -> x_norm[bs,seq,dim]
    return output * self.weight
### Test: RMSNorm Code ###
# You need take out the triple quotes below to perform testing
"""
x = torch.randn((ModelArgs.max_batch_size, ModelArgs.max_seq_len, ModelArgs.dim), device=device)
rms_norm = RMSNorm(dim=ModelArgs.dim)
x_norm = rms_norm(x)
print(f"Shape of x: {x.shape}")
print(f"Shape of x_norm: {x_norm.shape}")
"""
### Test Results: ###
"""
Shape of x: torch.Size([10, 256, 512])
Shape of x_norm: torch.Size([10, 256, 512])
"""

2b. 旋转位置编码（RoPE）：

为什么我们需要旋转位置编码（RoPE）？在讨论 “为什么 ”之前，让我们先回顾一下迄今为止我们所做的工作。首先，我们将输入文本转换为嵌入式文本。接着，我们将 RMSNorm 应用于嵌入式编码。说到这里，你一定发现了一些不对劲的地方。假设输入文本是 “我爱苹果 ”或 “苹果爱我”，模型仍然会将这两个句子视为相同，并以此进行学习。因为在嵌入模型中没有定义学习的顺序。因此，顺序对任何语言模型都非常重要。在 Llama 3 模型架构中，RePE 用于定义每个标记在句子中的位置，它不仅能保持顺序，还能保持标记在句子中的相对位置。

那么，什么是旋转位置编码（Rotary Positional Encoding），它又是如何工作的呢？如上文 “为什么 ”部分所述，RoPE 是一种位置编码方式，它通过添加绝对位置信息来对嵌入进行编码，从而保持了句子中标记的顺序，同时还包含了标记间的相对位置信息。它通过一个名为旋转矩阵的特殊矩阵旋转给定的嵌入来执行编码操作。这种使用旋转矩阵进行的简单但非常强大的数学推导是 RoPE 的核心。

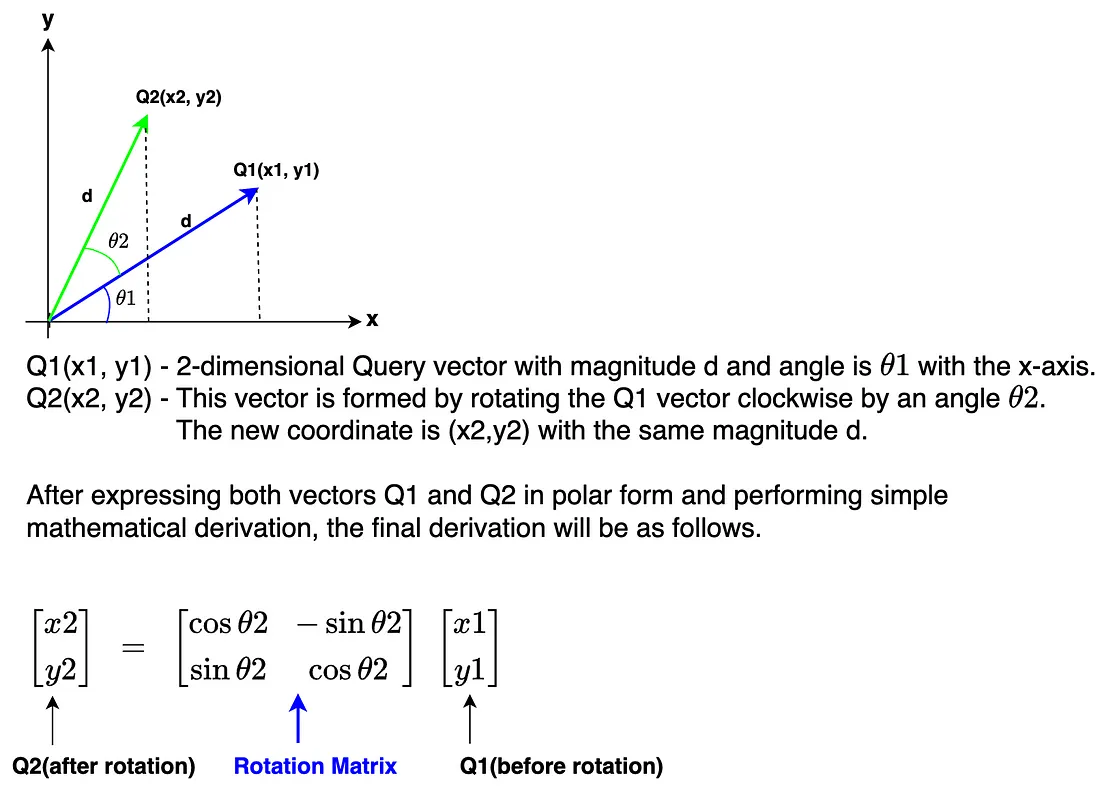
上图中的旋转矩阵旋转的是一个 2 维向量。然而，Llama 3 模型的维数是 4096，要多得多。让我们来看看如何对更高维度的嵌入应用旋转。

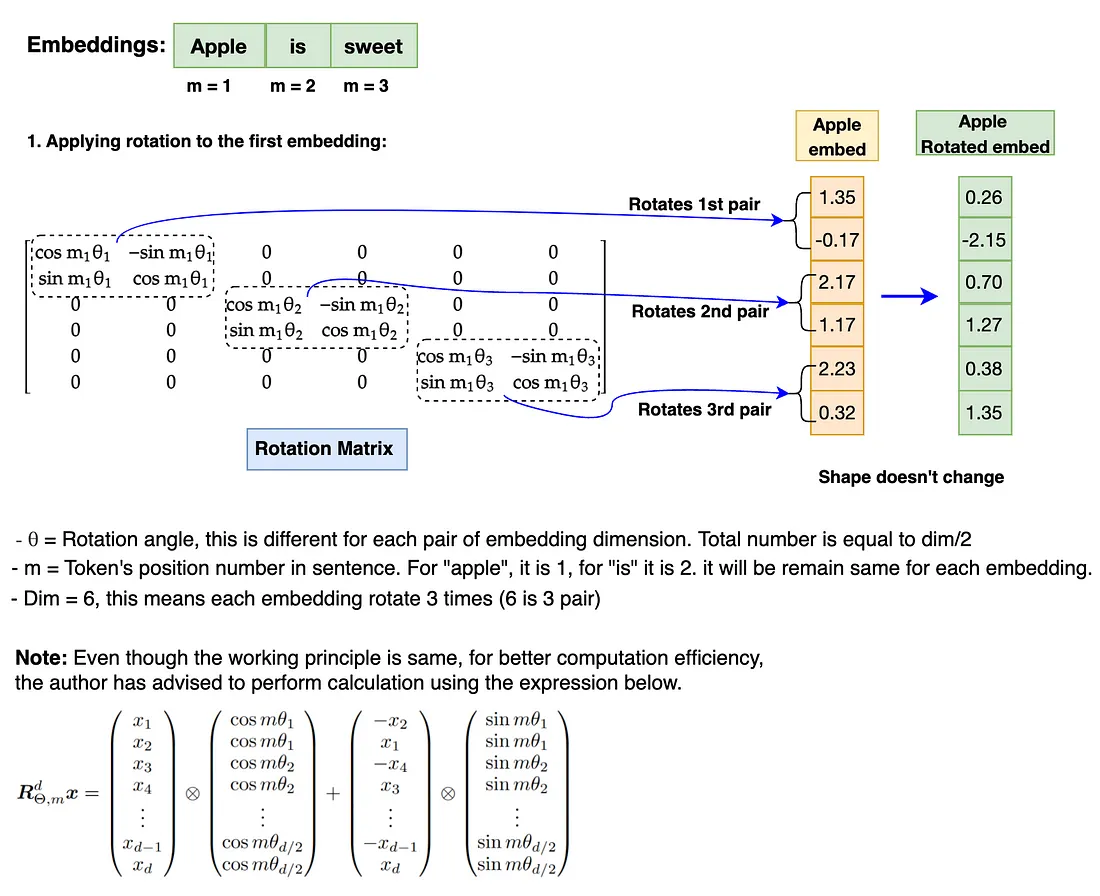
我们现在知道，嵌入的旋转涉及每对嵌入维度的每个嵌入位置 (m) 值和 theta (θ) 值的乘积。这就是 RoPE 如何通过旋转矩阵的实现来捕捉绝对位置和相对位置信息。

注意：在执行旋转之前，旋转矩阵需要转换为极坐标形式，嵌入向量需要转换为复数形式。旋转完成后，需要将旋转后的嵌入向量转换回实数，以便进行注意操作。此外，RoPE 仅适用于查询和键嵌入。它不适用于值嵌入。

让我们深入了解一下 RoPE 编码：

## Step2b: The RoPE
def precompute_freqs_cis(dim:int, seq_len: int, theta: float=10000.0):
  # Computing Theta value for each dim pair which is dim/2
  device = ModelArgs.device
  freqs = 1.0 / (theta ** (torch.arange(0, dim, 2,device=device)[:(dim//2)].float()/dim))
  # Computing range of positions(m) in the sequence
  t = torch.arange(seq_len, dtype=torch.float32, device=device)
  # freqs gives all the Theta value range for all the position of tokens in the sequence
  freqs = torch.outer(t, freqs).to(device)
  # This is the rotation matrix which needs to be converted to Polar form in order to perform rotation to the embedding
  freqs_cis = torch.polar(torch.ones_like(freqs).to(device), freqs).to(device)
  return freqs_cis
def reshape_for_broadcast(freqs_cis, x):
  ndim = x.ndim
  assert 0<=1<ndim
  assert freqs_cis.shape == (x.shape[1],x.shape[-1]), "the last two dimension of freqs_cis, x must match"
  shape = [d if i==1 or i==ndim-1 else 1 for i,d in enumerate(x.shape)]
  return freqs_cis.view(*shape)
def apply_rotary_emb(xq: torch.Tensor, xk: torch.Tensor, freqs_cis: torch.Tensor)->Tuple[torch.Tensor, torch.Tensor]:
  device = ModelArgs.device
  # Applying rotary positional encoding to both query and key embedding together
  # First: The last dimension of xq and xk embedding needs to be reshaped to make it a pair. As rotation matrix is applied to each pair of dim.
  # Next: convert both xq and xk to complex number as the rotation matrix is only applicable to complex number
  xq_ = torch.view_as_complex(xq.float().reshape(*xq.shape[:-1], -1, 2)).to(device)    #xq_:[bsz, seq_len, n_heads, head_dim/2]
  xk_ = torch.view_as_complex(xk.float().reshape(*xk.shape[:-1], -1, 2)).to(device)    #xk_:[bsz, seq_len, n_heads, head_dim/2]
  # The rotation matrix(freqs_cis) dimensions across seq_len(dim=1) and head_dim(dim=3) should match with the embedding
  # Also, the shape freqs_cis should be the same with xq and xk, hence change the shape of freqs_cis:[seq_len,head_dim] -> freqs_cis:[1,seq_len,1,head_dim]
  freqs_cis = reshape_for_broadcast(freqs_cis, xq_)
  #Finally, perform rotation operation by multiplying with freqs_cis.
  #After the rotation is completed, convert both xq_out and xk_out back to real number and return
  xq_out = torch.view_as_real(xq_ * freqs_cis).flatten(3).to(device) #xq_out:[bsz, seq_len, n_heads, head_dim]
  xk_out = torch.view_as_real(xk_ * freqs_cis).flatten(3).to(device) #xk_out:[bsz, seq_len, n_heads, head_dim]
  return xq_out.type_as(xq), xk_out.type_as(xk)
### Test: RoPE Code ###
# Note: x_norm is calculated during RMSNorm and is being used for testing here.
# You need take out the triple quotes below to perform testing
"""
head_dim = ModelArgs.dim//ModelArgs.n_heads
wq = nn.Linear(ModelArgs.dim, ModelArgs.n_heads * head_dim, bias=False, device=device)
wk = nn.Linear(ModelArgs.dim, ModelArgs.n_kv_heads * head_dim, bias=False, device=device)
xq = wq(x_norm)
xk = wk(x_norm)
print(f"xq.shape: {xq.shape}")
print(f"xk.shape: {xk.shape}")
xq = xq.view(xq.shape[0],xq.shape[1],ModelArgs.n_heads, head_dim)
xk = xk.view(xk.shape[0],xk.shape[1],ModelArgs.n_kv_heads, head_dim)
print(f"xq.re-shape: {xq.shape}")
print(f"xk.re-shape: {xk.shape}")
freqs_cis = precompute_freqs_cis(dim=head_dim, seq_len=ModelArgs.max_seq_len)
print(f"freqs_cis.shape: {freqs_cis.shape}")
xq_rotate, xk_rotate = apply_rotary_emb(xq, xk, freqs_cis)
print(f"xq_rotate.shape: {xq_rotate.shape}")
print(f"xk_rotate.shape: {xk_rotate.shape}")
"""
### Test Results: ###
"""
xq.shape: torch.Size([10, 256, 512])
xk.shape: torch.Size([10, 256, 256])
xq.re-shape: torch.Size([10, 256, 8, 64])
xk.re-shape: torch.Size([10, 256, 4, 64])
freqs_cis.shape: torch.Size([256, 32])
xq_rotate.shape: torch.Size([10, 256, 8, 64])
xk_rotate.shape: torch.Size([10, 256, 4, 64])
"""

2c. KV 缓存（仅推理时需要）：

什么是 KV 缓存？在 Llama 3 架构中，推理时引入了 KV 缓存的概念，以键和值缓存的形式存储之前生成的令牌。这些缓存将用于计算自注意力，以生成下一个标记。只有键和值令牌才会被缓存，而查询令牌则不会被缓存，因此称为 KV 缓存。

为什么需要 KV 缓存？让我们看看下图，以澄清我们的好奇心。

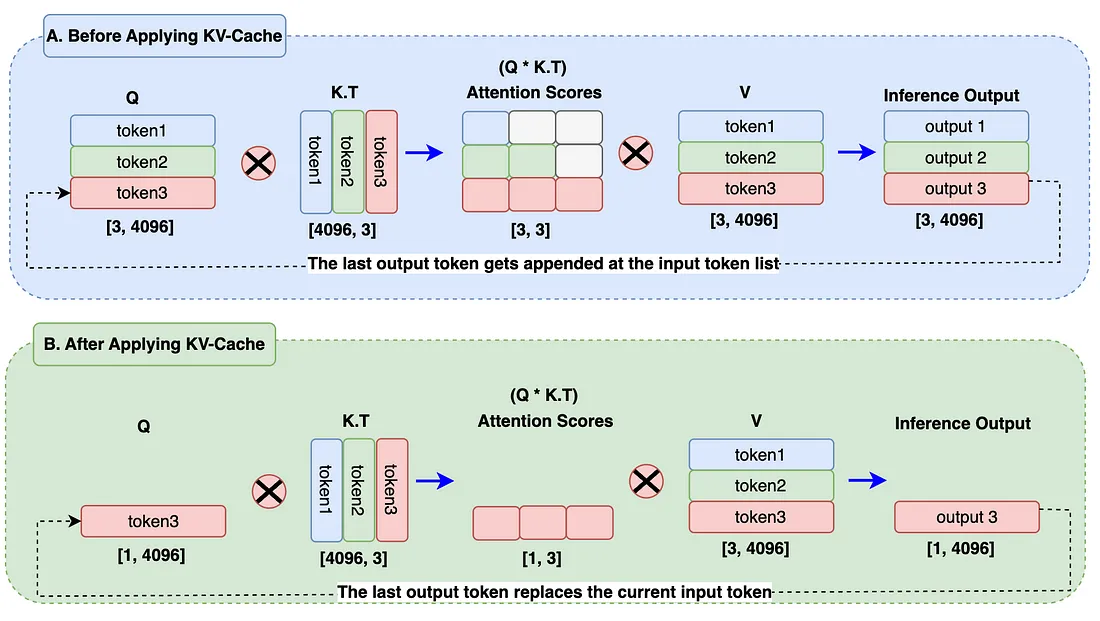
• 在图中的 A 图块中，在生成输出 3 标记时，仍在计算之前的输出标记（输出 1、输出 2），而这是完全没有必要的。这在注意力计算过程中造成了额外的矩阵乘法，从而大大增加了计算资源。
• 在图中的 B 块，输出标记取代了查询嵌入中的输入标记。KV 缓存会存储之前生成的标记。在计算注意力分数时，我们只需使用查询中的一个标记，并使用键和值缓存中以前的标记。它将从块 A 到块 B 的矩阵乘法从 3x3 减少到 1x3，减少了近 66%。在现实世界中，由于序列长度和批量大小都很大，这将有助于大幅降低计算能力。最后，生成的最新输出标记始终只有一个。这就是引入 KV-Cache 的主要原因。

2d. 分组查询关注：

分组查询注意力与之前的模型（如 Llama 1）中使用的 Muilt Head 注意力相同，唯一的区别是查询使用不同的头，键/值使用不同的头。通常，分配给查询的 “头 ”数是键和值 “头 ”数的 n 倍。让我们看一下图表，进一步加深理解。

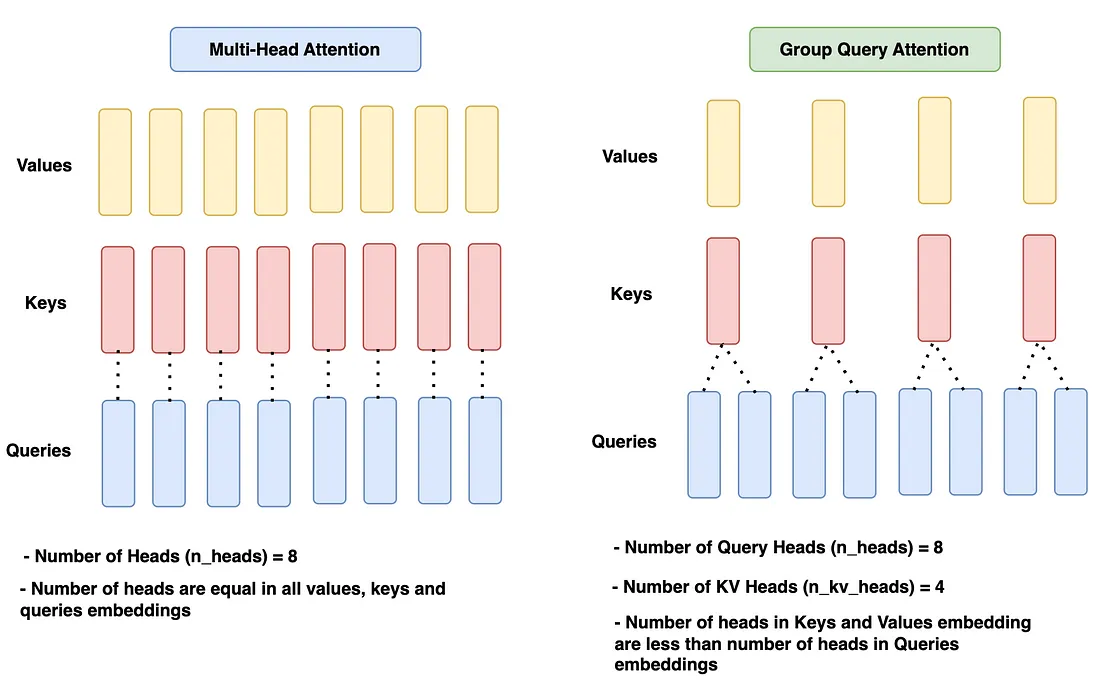
在给定的图表中，多头注意力在所有查询、键和值中的头数相等，即 n_heads = 8。

分组查询注意模块的查询头数为 8 个（n_heads），键和值的查询头数为 4 个（n_kv_heads），比查询头数少 2 倍。

既然 MultiHead Attention 已经这么好了，为什么还需要 Group query Attention？要回答这个问题，我们需要先回顾一下 KV Cache。KV Cache 有助于大大减少计算资源。然而，随着 KV Cache 存储越来越多的先前 token，内存资源将显著增加。这对于模型性能和财务角度来说都不是一件好事。因此，引入了 Group query Attention。减少 K 和 V 的 head 数量会减少要存储的参数数量，因此使用的内存更少。各种测试结果证明，采用这种方法，模型准确率保持在同一范围内。

让我们用代码来实现这一点：

## The Attention Block [Step2c: The KV Cache; Step2d: Group Query Attention]
## As mentioned before, the naming convention follows original the meta's LLama3 GitHub
class Attention(nn.Module):
  def __init__(self, args: ModelArgs):
    super().__init__()
    self.args = args
    # Embedding dimension
    self.dim = args.dim
    # Number of heads assigned to Query
    self.n_heads = args.n_heads
    # Number of heads assigned to Key and values. If "None", the number will be same as Query.
    self.n_kv_heads = args.n_heads if args.n_kv_heads is None else args.n_kv_heads
    # Dimension of each head relative to model dimension
    self.head_dim = args.dim // args.n_heads
    # Number of repetition in order to make time Key, Value heads to match Query heads number
    self.n_rep = args.n_heads // args.n_kv_heads
    # Weight initialize for Keys, Querys, Values and Oupt. Notice that the out_feature value of weight for q and kv are based on it's heads
    self.wq = nn.Linear(self.dim, self.n_heads * self.head_dim, bias=False, device=device)
    self.wk = nn.Linear(self.dim, self.n_kv_heads * self.head_dim, bias=False, device=device)
    self.wv = nn.Linear(self.dim, self.n_kv_heads * self.head_dim, bias=False, device=device)
    self.wo = nn.Linear(self.n_heads * self.head_dim, self.dim, bias=False, device=device)
    # Initialize caches to store Key, Values at start. (KV Cache Implementation)
    self.cache_k = torch.zeros((args.max_batch_size, args.max_seq_len, self.n_kv_heads, self.head_dim), device=args.device)
    self.cache_v = torch.zeros((args.max_batch_size, args.max_seq_len, self.n_kv_heads, self.head_dim), device=args.device)
  def forward(self, x: torch.Tensor, start_pos, inference):
    # Shape of the input embedding: [bsz,seq_len,dim]
    bsz, seq_len, _ = x.shape
    # Mask will be used during 'Training' and is not required for 'inference' due to the use of KV cache.
    mask = None
    xq = self.wq(x)  #x[bsz,seq_len,dim]*wq[dim,n_heads * head_dim] -> q[bsz,seq_len,n_heads * head_dim]
    xk = self.wk(x)  #x[bsz,seq_len,dim]*wq[dim,n_kv_heads * head_dim] -> k[bsz,seq_len,n_kv_heads * head_dim]
    xv = self.wv(x)  #x[bsz,seq_len,dim]*wq[dim,n_kv_heads * head_dim] -> v[bsz,seq_len,n_kv_heads * head_dim]
    # Reshaping Querys, Keys and Values by their number of heads. (Group Query Attention Implementation)
    xq = xq.view(bsz, seq_len, self.n_heads, self.head_dim)      #xq[bsz,seq_len,n_heads, head_dim]
    xk = xk.view(bsz, seq_len, self.n_kv_heads, self.head_dim)   #xk[bsz,seq_len,n_kv_heads, head_dim]
    xv = xv.view(bsz, seq_len, self.n_kv_heads, self.head_dim)   #xv[bsz,seq_len,n_kv_heads, head_dim]
    # Model - Inference Mode: kv-cache is enabled at inference mode only.
    if inference:
      # Compute rotation matrix for each position in the sequence
      freqs_cis = precompute_freqs_cis(dim=self.head_dim, seq_len=self.args.max_seq_len * 2)
      # During inferencing, we should only take the rotation matrix range from the current position of the tokens.
      freqs_cis = freqs_cis[start_pos : start_pos + seq_len]
      # Apply RoPE to Queries and Keys embeddings
      xq, xk = apply_rotary_emb(xq, xk, freqs_cis)
      self.cache_k = self.cache_k.to(xq)
      self.cache_v = self.cache_v.to(xq)
      # Store Keys and Values token embedding into their respective cache [KV Cache Implementation]
      self.cache_k[:bsz, start_pos:start_pos + seq_len] = xk
      self.cache_v[:bsz, start_pos:start_pos + seq_len] = xv
      # Assign all the previous tokens embeddings upto current tokens position to Keys and Values variable for Attention Calculation
      keys = self.cache_k[:bsz, :start_pos + seq_len]
      values = self.cache_v[:bsz, :start_pos + seq_len]
      # At this point, they Keys and Values shape aren't same with Queries Embedding which has to be in order to computer attention score
      # Use repeat_kv function to make Keys,Values shape same as queries shape
      keys = repeat_kv(keys, self.n_rep)      #keys[bsz,seq_len,n_heads,head_dim]
      values = repeat_kv(values, self.n_rep)  #values[bsz,seq_len,n_heads,head_dim]
    # Mode - Training mode: KV-Cache not implemented
    else:
      # Compute rotation matrix and apply RoPE to queries and keys for for training.
      freqs_cis = precompute_freqs_cis(dim=self.head_dim, seq_len=self.args.max_seq_len)
      #xq[bsz,seq_len,n_heads, head_dim], xk[bsz,seq_len,n_heads, head_dim]
      xq, xk = apply_rotary_emb(xq, xk, freqs_cis)
      # Use repeat_kv function to make Keys,Values shape same as the queries shape
      #keys[bsz,seq_len,n_heads,head_dim], #values[bsz,seq_len,n_heads,head_dim]
      keys = repeat_kv(xk, self.n_rep)
      values = repeat_kv(xv, self.n_rep)
      # For training mode, we'll compute mask and apply to the attention score later
      mask = torch.full((seq_len, seq_len),float("-inf"),device=self.args.device)
      mask = torch.triu(mask, diagonal=1).to(self.args.device)
    # To compute attention, we'll need to perform a transpose operation to reshape all queries, keys and values bring heads at dim 1 and seq at dim 2
    xq = xq.transpose(1,2)                  #xq[bsz,n_heads,seq_len,head_dim]
    keys = keys.transpose(1,2)              #keys[bsz,n_heads,seq_len,head_dim]
    values = values.transpose(1,2)          #values[bsz,n_heads,seq_len,head_dim]
    # Computing attention score
    scores = torch.matmul(xq, keys.transpose(2,3)).to(self.args.device)/math.sqrt(self.head_dim)
    if mask is not None:
      scores = scores + mask
    # Apply softmax to the attention score
    scores = F.softmax(scores.float(), dim=-1).type_as(xq)
    # Matrix multiplication of attention score with the values
    output = torch.matmul(scores, values).to(self.args.device)
    # We get the contextual embedding for each head
    # All heads need to be reshaped back and combined to give a single single contextual attention output
    # Shape change: output[bsz,n_heads,seq_len,head_dim] -> output[bsz,seq_len, n_heads,head_dim] -> output[bsz,seq_len, n_heads * head_dim]
    output = output.transpose(1,2).contiguous().view(bsz, seq_len, -1)
    # shape: output [bsz,seq_len,dim]
    return self.wo(output)
# If the number of keys/values heads is less than query heads, this function expands the key/values embeddings with the required number of repetition
def repeat_kv(x:torch.Tensor, n_rep: int)-> torch.Tensor:
  bsz, seq_len, n_kv_heads, head_dim = x.shape
  if n_rep == 1:
    return x
  return (
      x[:,:,:,None,:]
      .expand(bsz,seq_len,n_kv_heads,n_rep, head_dim)
      .reshape(bsz,seq_len,n_kv_heads * n_rep, head_dim)
  )

### Test: Repeat_kv function ###
# note: xk, x_norm is already calculated during RoPE, RMSNorm testing and is being used for testing here.
# You need take out the triple quotes below to perform testing
"""
n_rep = ModelArgs.n_heads // ModelArgs.n_kv_heads
keys = repeat_kv(xk, n_rep)
print(f"xk.shape: {xk.shape}")
print(f"keys.shape: {keys.shape}")
## Test: Attention function
# You need take out the triple quotes below to perform testing
attention = Attention(ModelArgs)
x_out = attention(x_norm,start_pos=0, inference=False)
print(f"x_out.shape: {x_out.shape}")
"""
### Test Results: ###
"""
xk.shape: torch.Size([10, 256, 4, 64])
keys.shape: torch.Size([10, 256, 8, 64])
x_out.shape: torch.Size([10, 256, 512])
"""

2e. 前馈网络（SwiGLU 激活）：

前馈网络在解码器模块中的作用是什么？如上图所示，注意力输出首先经过 RMSNorm 归一化处理，然后输入前馈网络。在前馈网络中，注意力输出嵌入将在整个隐藏层中扩展到更高的维度，并学习更复杂的标记特征。

为什么使用 SwiGLU 而不是 ReLU？让我们看看图表就能找到答案。

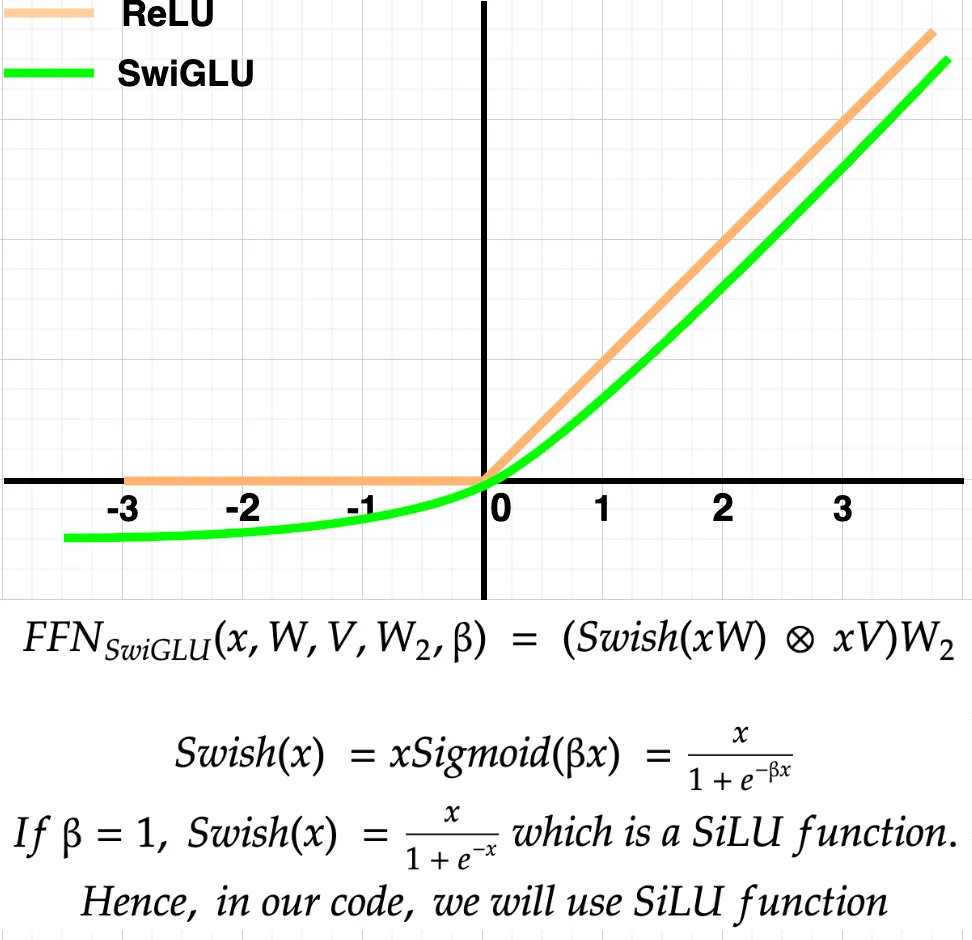
正如上图所示，SwiGLU函数在正轴上的行为几乎类似于ReLU函数。然而，在负轴上，SwiGLU输出一些负值，在学习较小的值时可能比ReLU的平坦0更有用。总的来说，根据作者的说法，使用SwiGLU的性能比使用ReLU要好，因此被选择了。

现在让我们深入了解前馈（FeedForward）代码。

## Step2e: The Feedfoward Network (SwiGLU activation)
class FeedForward(nn.Module):
  def __init__(self, dim:int, hidden_dim:int, multiple_of:int, ffn_dim_multiplier: Optional[float]):
    super().__init__()
    # Models embedding dimension
    self.dim = dim
    # We must use the hidden dimensions calculation shared by Meta which is the ideal one for this model
    # Hidden dimension are calculated such that it is a multiple of 256.
    hidden_dim = int(2 * hidden_dim/3)
    if ffn_dim_multiplier is not None:
      hidden_dim = int(ffn_dim_multiplier * hidden_dim)
    hidden_dim = multiple_of * ((hidden_dim + multiple_of - 1) // multiple_of)
    # define hiddne layers weights
    self.w1 = nn.Linear(self.dim, hidden_dim, bias=False, device=device)
    self.w2 = nn.Linear(hidden_dim, self.dim, bias=False, device=device)
    self.w3 = nn.Linear(self.dim, hidden_dim, bias=False, device=device)
  def forward(self, x):
    # Shape: [bsz,seq_len,dim]
    return self.w2(F.silu(self.w1(x)) * self.w3(x))


### Test: FeedForward module ###
# note: x_out is already computed at Attention testing and is being used for testing here.
# You need take out the triple quotes below to perform testing
"""
feed_forward = FeedForward(ModelArgs.dim, 4 * ModelArgs.dim, ModelArgs.multiple_of, ModelArgs.ffn_dim_multiplier)
x_out = rms_norm(x_out)
x_out = feed_forward(x_out)
print(f"feed forward output: x_out.shape: {x_out.shape}")
"""
### Test Results: ###
"""
feed forward output: x_out.shape: torch.Size([10, 256, 512])
"""

2f. 解码器块：

如上面的架构图所示（第一个图表），解码器块由多个子组件组成，我们在前几个部分（2a-2f）中已经学习并编写了代码。以下是在解码器块中正在进行的点操作。

1. 输入块中的嵌入被输入到 Attention-RMSNorm 块中。这将进一步输入到 Group Query Attention 块中。
2. 然后，来自输入块的相同嵌入将被添加到注意力输出中。
3. 之后，注意力输出被馈入 FeedFoward-RMSNorm，并进一步馈入 FeedFoward 网络块。
4. 然后将 FeedFoward 网络的输出再次与注意力输出相加。
5. 产生的输出称为解码器输出。然后，此解码器输出被馈送到另一个解码器块作为输入。接下来的 31 个解码器块将重复此相同操作。然后，第 32 个解码器块的最终解码器输出被传递到输出块。

请看下面的代码来了解这个过程。

## Step2f: The Decoder Block. The class name is assigned as TransformerBlock to match the name of Meta llama 3 code base.
class TransformerBlock(nn.Module):
  def __init__(self, args: ModelArgs):
    super().__init__()
    self.args = args
    # Initilizate RMSNorm for attention
    self.attention_norm = RMSNorm(dim=args.dim, eps = args.norm_eps)
    # Initilizate Attention class
    self.attention = Attention(args)
    # Initilizate RMSNorm for feedfoward class
    self.ff_norm = RMSNorm(dim=args.dim, eps = args.norm_eps)
    # Initilizate feedfoward class
    self.feedforward = FeedForward(args.dim, 4 * args.dim, args.multiple_of, args.ffn_dim_multiplier)
  def forward(self, x, start_pos, inference):
    # start_pos = token position for inference mode, inference = True for inference and False for training mode
    # i) pass input embedding to attention_norm and then pass to attention block.
    # ii) the output of attention is then added to embedding(before norm)
    h = x + self.attention(self.attention_norm(x), start_pos, inference)
    # i) pass attention output to ff_norm and then pass to the feedforward network.
    # ii) the output of feedforward network is then added to the attention output(before ff_norm)
    out = h + self.feedforward(self.ff_norm(h))
    # Shape: [bsz,seq_len,dim]
    return out

### Test: TransformerBlock ###
# You need take out the triple quotes below to perform testing
"""
x = torch.randn((ModelArgs.max_batch_size, ModelArgs.max_seq_len, ModelArgs.dim), device=device)
transformer_block = TransformerBlock(ModelArgs)
transformer_block_out = transformer_block(x,start_pos=0, inference=False)
print(f"transformer_block_out.shape: {transformer_block_out.shape}")
"""
### Test Results: ###
"""
transformer_block_out.shape: torch.Size([10, 64, 128])
"""

第三步：输出块

最后一个解码器块的解码器输出将馈送到输出块。首先，它将被送入RMSNorm中。然后，它将被送入线性层（Linear Layer），该层生成logits。接下来，将执行以下两个操作之一。

• 如果模式是推理（inference），将计算top_p概率并生成下一个标记。生成的下一个标记将在达到最大生成长度或生成结束句标记作为下一个标记时停止。
• 如果模式是训练（Training），将使用目标标签计算损失，并重复训练直到达到最大迭代次数。

让我们看一下输出块的流程图，以获得更加清晰的理解。

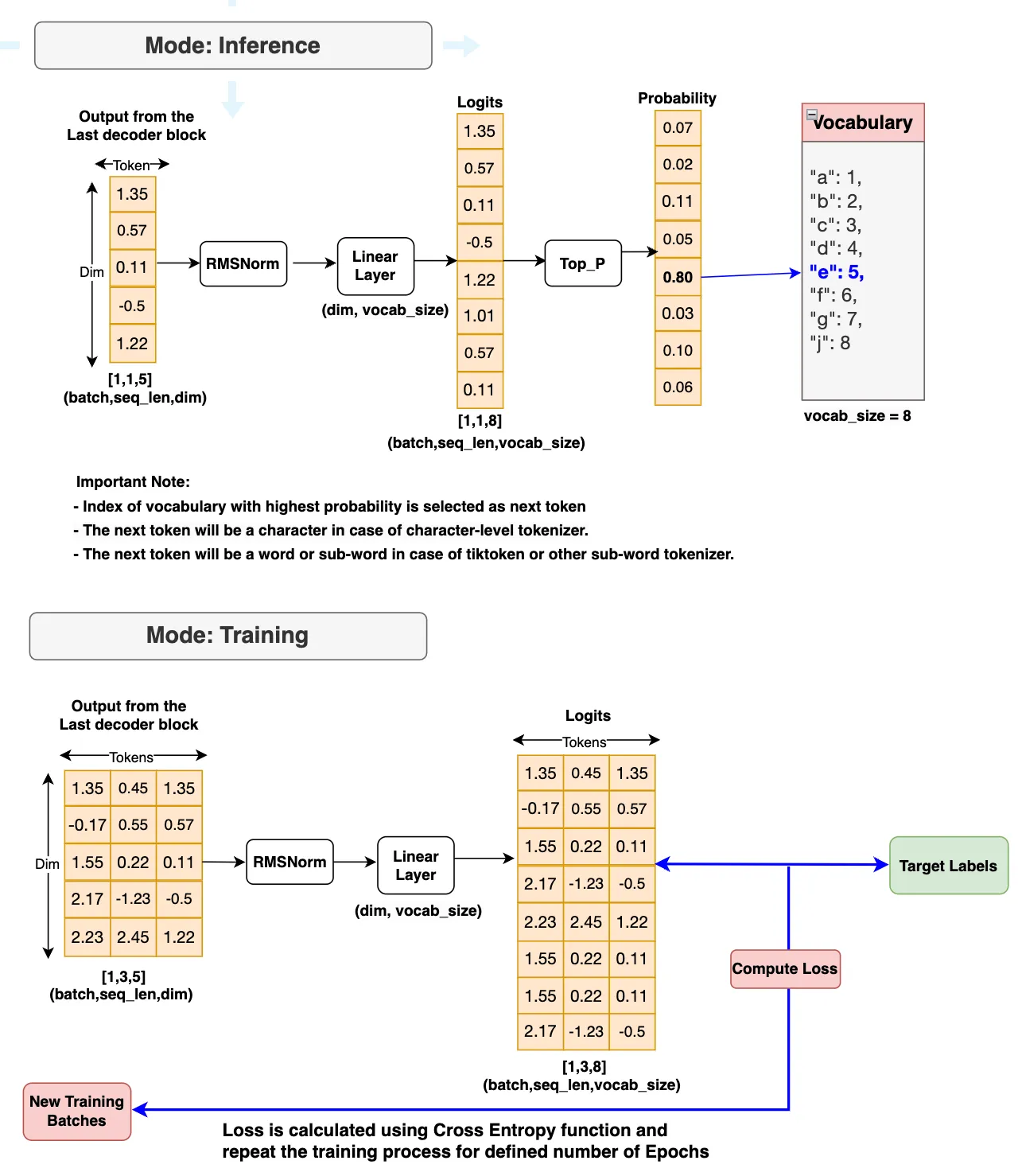
最后，让我们将输入块、解码器块和输出块的所有组件结合起来，得到我们的最终Llama 3模型。

让我们编写最终的Llama 3模型吧。

## Step3: The Output Block
# This is the Llama 3 model. Again, the class name is maintained as Transformer to match with Meta Llama 3 model.
class Transformer(nn.Module):
  def __init__(self, params: ModelArgs):
    super().__init__()
    # set all the ModelArgs in params variable
    self.params = params
    # Initilizate embedding class from the input block
    self.tok_embeddings = nn.Embedding(params.vocab_size, params.dim)
    # Initialize the decoder block and store it inside the ModuleList. 
    # This is because we've 4 decoder blocks in our Llama 3 model. (Official Llama 3 has 32 blocks)
    self.layers = nn.ModuleList()
    for layer_id in range(params.n_layers):
      self.layers.append(TransformerBlock(args=params))
    # Initilizate RMSNorm for the output block
    self.norm = RMSNorm(params.dim, eps = params.norm_eps)
    
    # Initilizate linear layer at the output block.
    self.output = nn.Linear(params.dim, params.vocab_size, bias=False)
  def forward(self, x, start_pos=0, targets=None):
    
    # start_pos = token position for inference mode, inference = True for inference and False for training mode
    # x is the batch of token_ids generated from the texts or prompts using tokenizers.
    # x[bsz, seq_len] -> h[bsz, seq_len, dim]
    h = self.tok_embeddings(x)
    # If the target is none, Inference mode is activated and set to "True" and "False" if Training mode is activated.
    if targets is None:
      inference = True
    else:
      inference = False
    # The embeddings (h) will then pass though all the decoder blocks.
    for layer in self.layers:
      h = layer(h, start_pos, inference)
    # The output from the final decoder block will feed into the RMSNorm
    h = self.norm(h)
    # After normalized, the embedding h will then feed into the Linear layer. 
    # The main task of the Linear layer is to generate logits that maps the embeddings with the vocabulary size.
    # h[bsz, seq_len, dim] -> logits[bsz, seq_len, vocab_size]
    logits = self.output(h).float()
    loss = None
    # Inference mode is activated if the targets is not available
    if targets is None:
      loss = None
    # Training mode is activated if the targets are available. And Loss will be calculated for further model training. 
    else:
      loss = F.cross_entropy(logits.view(-1, self.params.vocab_size), targets.view(-1))
    return logits, loss

### Test: Transformer (Llama Model) ###
# You need take out the triple quotes below to perform testing
"""
model = Transformer(ModelArgs).to(ModelArgs.device)
print(model)
"""

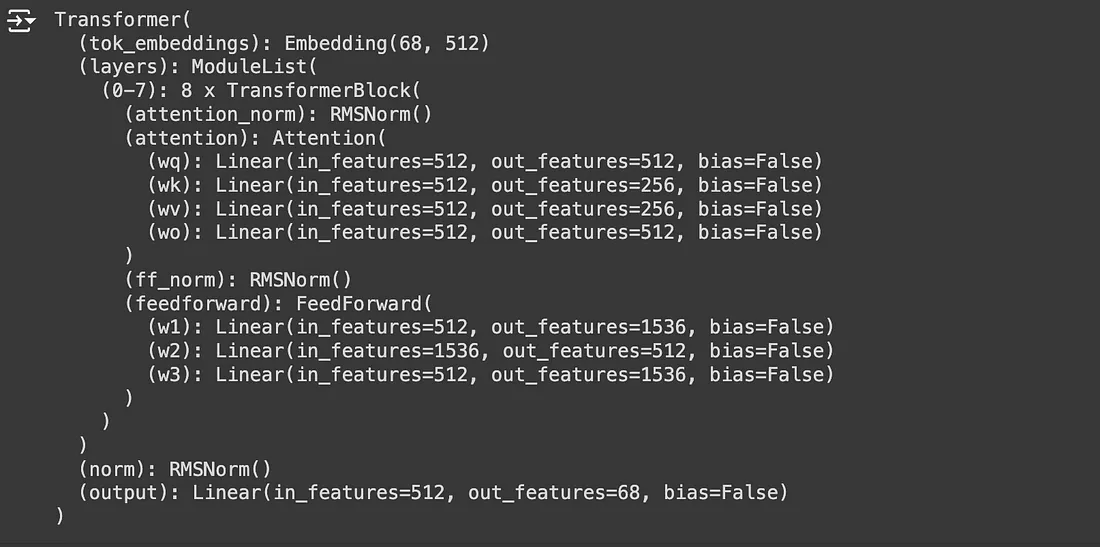
我们刚刚构建的Llama 3模型看起来非常完美。我们现在准备开始训练过程。

第4步：训练我们的Llama 3模型：

训练流程在输出块流程图中已经提供（第3步）。如果你在开始训练之前需要更清晰的说明，请再次参考该流程。让我们开始编写训练代码。我也会在代码块中提供必要的解释。

## Step 4: Train Llama 3 Model:
# Create a dataset by encoding the entire tiny_shakespeare data token_ids list using the tokenizer's encode function that we've built at the input block section
dataset = torch.tensor(encode(data), dtype=torch.int).to(ModelArgs.device)
print(f"dataset-shape: {dataset.shape}")
# Define function to generate batches from the given dataset
def get_dataset_batch(data, split, args:ModelArgs):
  seq_len = args.max_seq_len
  batch_size = args.max_batch_size
  device = args.device
  train = data[:int(0.8 * len(data))]
  val = data[int(0.8 * len(data)): int(0.9 * len(data))]
  test = data[int(0.9 * len(data)):]
  batch_data = train
  if split == "val":
    batch_data = val
  if split == "test":
    batch_data = test
  
  # Picking random starting points from the dataset to give random samples for training, validation and testing.
  
  ix = torch.randint(0, len(batch_data) - seq_len - 3, (batch_size,)).to(device)
  x = torch.stack([torch.cat([token_bos, batch_data[i:i+seq_len-1]]) for i in ix]).long().to(device)
  y = torch.stack([torch.cat([batch_data[i+1:i+seq_len], token_eos]) for i in ix]).long().to(device)
  
  return x,y
### Test: get_dataset function ###
"""
xs, ys = get_dataset_batch(dataset, split="train", args=ModelArgs)
print([(decode(xs[i].tolist()), decode(ys[i].tolist())) for i in range(len(xs))])
"""
# Define a evaluate loss function to calculate and store training and validation loss for logging and plotting
@torch.no_grad()
def evaluate_loss(model, args:ModelArgs):
  out = {}
  model.eval()
  for split in ["train", "val"]:
    losses = []
    for _ in range(10):      
      xb, yb = get_dataset_batch(dataset, split, args)
      _, loss = model(x=xb, targets=yb)
      losses.append(loss.item())
    out[split] = np.mean(losses)
  model.train()
  return out
# Define a training function to perform model training
def train(model, optimizer, args:ModelArgs):
    epochs = args.epochs
    log_interval = args.log_interval
    device = args.device
    losses = []   
    start_time = time.time()
    for epoch in range(epochs):
        optimizer.zero_grad()
        
        xs, ys = get_dataset_batch(dataset, 'train', args)
        xs = xs.to(device)
        ys = ys.to(device)
        logits, loss = model(x=xs, targets=ys)
        loss.backward()
        optimizer.step()
        if epoch % log_interval == 0:
            batch_time = time.time() - start_time
            x = evaluate_loss(model, args)
            losses += [x]            
            print(f"Epoch {epoch} | val loss {x['val']:.3f} | Time {batch_time:.3f}")
            start_time = time.time()
    
    # Print the final validation loss
    print("validation loss: ", losses[-1]['val'])
    # Display the interval losses in plot 
    return pd.DataFrame(losses).plot()

现在，我们已经定义了训练函数。让我们使用以下代码块开始训练，并在训练完成后观察绘图结果。

## Start training our Llama 3 model
model = Transformer(ModelArgs).to(ModelArgs.device)
optimizer = torch.optim.Adam(model.parameters())
train(model, optimizer, ModelArgs)

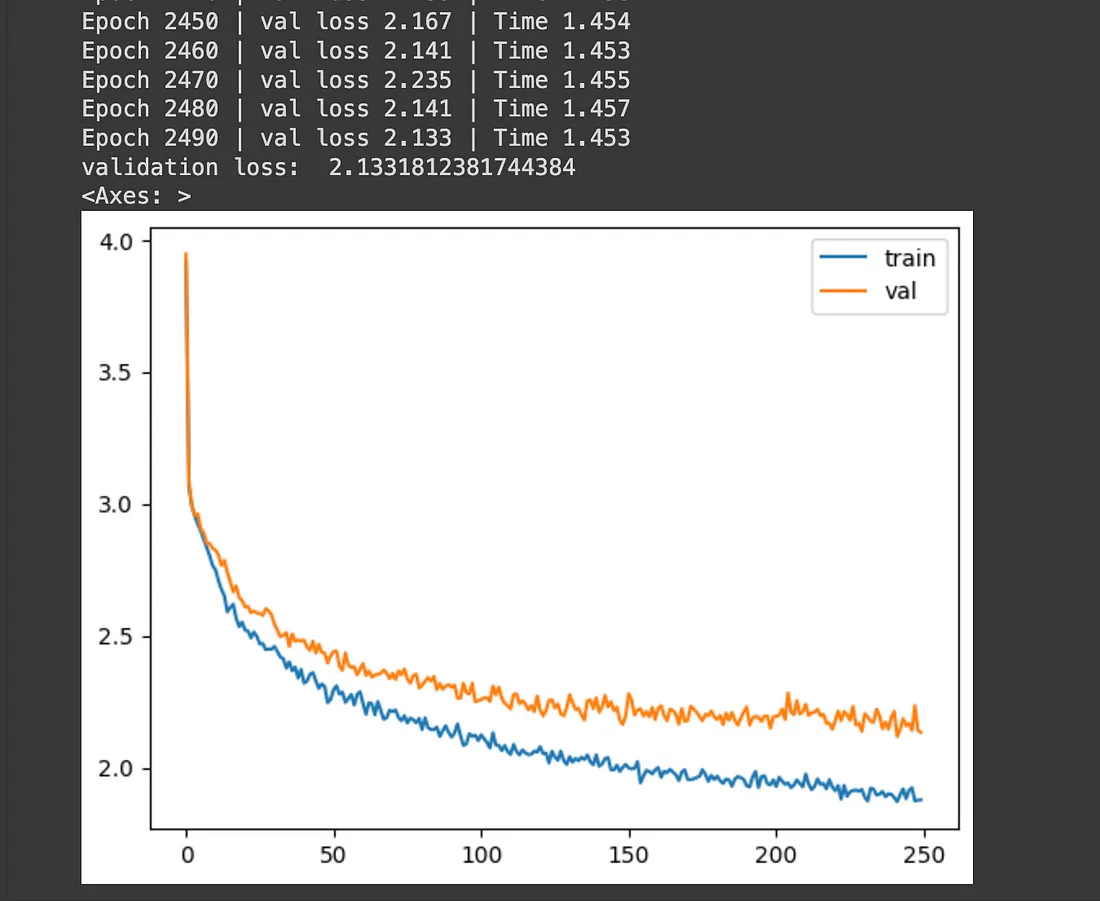
上图显示了训练和验证损失图。训练已进行了2500个epochs。在使用默认GPU和RAM设置的Google Colab上，训练过程大约花费了10分钟，速度非常快。最终epoch的验证损失为2.19，考虑到我们使用的训练数据量和迭代次数，这是可以接受的。要显著降低损失，我们需要增加训练数据的大小、增加迭代次数以及增加GPU或处理能力。

现在我们已经完成了训练。让我们进入最后一步-推理（Inference），看看模型在给定新输入提示时生成的输出文本有多好。

第5步：推理Llama 3模型：

推理流程在输出块流程图中已经提供（第3步）。让我们开始编写推理代码。

## Step 5: Inference Llama 3 Model:
# This function generates text sequences based on provided prompts using the LLama 3 model we've built and trained.
def generate(model, prompts: str, params: ModelArgs, max_gen_len: int=500, temperature: float = 0.6, top_p: float = 0.9):
    # prompt_tokens: List of user input texts or prompts
    # max_gen_len: Maximum length of the generated text sequence.
    # temperature: Temperature value for controlling randomness in sampling. Defaults to 0.6.
    # top_p: Top-p probability threshold for sampling prob output from the logits. Defaults to 0.9.
    # prompt_tokens = [0]
    bsz = 1  #For inferencing, in general user just input one prompt which we'll take it as 1-batch
    prompt_tokens = token_bos.tolist() + encode(prompts)
    assert len(prompt_tokens) <= params.max_seq_len, "prompt token length should be small than max_seq_len"
    total_len = min(len(prompt_tokens)+max_gen_len, params.max_seq_len)   
    # this tokens matrix is to store the input prompts and all the output that is generated by model.
    # later we'll use the tokenizers decode function to decode this token to view results in text format
    tokens = torch.full((bsz,total_len), fill_value=token_pad.item(), dtype=torch.long, device=params.device)
    # fill in the prompt tokens into the token matrix
    tokens[:,:len(prompt_tokens)] = torch.tensor(prompt_tokens, dtype=torch.long, device=params.device)
    #create a prompt_mask_token for later use to identify if the token is a prompt token or a padding token
    # True if it is a prompt token, False if it is a padding token
    input_text_mask = tokens != token_pad.item()
    #now we can start inferencing using one token at a time from the prompt_tokens list starting with the first position.
    prev_pos = 0
    for cur_pos in range(1, total_len):
      with torch.no_grad():
        logits, _ = model(x=tokens[:,prev_pos:cur_pos], start_pos=prev_pos)
      if temperature > 0:      
        probs = torch.softmax(logits[:, -1]/temperature, dim=-1)
        next_token = sample_top_p(probs, top_p)        
      else:
        next_token = torch.argmax(logits[:, -1], dim=-1)        
      next_token = next_token.reshape(-1)
      # only replace the token if it's a padding token
      next_token = torch.where(input_text_mask[:, cur_pos], tokens[:, cur_pos], next_token)
      tokens[:, cur_pos] = next_token
      prev_pos = cur_pos
      if tokens[:,cur_pos]==token_pad.item() and next_token == token_eos.item():
        break
    output_tokens, output_texts = [], []    
    for i, toks in enumerate(tokens.tolist()):
      # eos_idx = toks.index(token_eos.item())
      if token_eos.item() in toks:
        eos_idx = toks.index(token_eos.item())
        toks = toks[:eos_idx]
      output_tokens.append(toks)
      output_texts.append(decode(toks))
    return output_tokens, output_texts
# Perform top-p (nucleus) sampling on a probability distribution.
# probs (torch.Tensor): Probability distribution tensor derived from the logits.
# p: Probability threshold for top-p sampling.
# According to the paper, Top-p sampling selects the smallest set of tokens whose cumulative probability mass exceeds the threshold p. 
# The distribution is renormalized based on the selected tokens.
def sample_top_p(probs, p):
    probs_sort, prob_idx = torch.sort(probs, dim=-1, descending=True)
    probs_sum = torch.cumsum(probs_sort, dim=-1)
    mask = probs_sum - probs_sort > p
    probs_sort[mask] = 0.0
    probs_sort.div_(probs_sort.sum(dim=-1, keepdim=True))
    next_token = torch.multinomial(probs_sort, num_samples=1)
    next_token = torch.gather(prob_idx, -1, next_token)    
    # Sampled token indices from the vocabular is returned 
    return next_token

让我们对新的提示进行推理并检查生成的输出。

## Perform the inferencing on user input prompts
prompts = "Consider you what services he has done"
output_tokens, output_texts = generate(model, prompts, ModelArgs)
output_texts = output_texts[0].replace("<|begin_of_text|>", "")
print(output_texts)
## Output ##
"""
Consider you what services he has done o eretrane
adetranytnn i eey i ade hs rcuh i eey,ad hsatsTns rpae,T
eon o i hseflns o i eee ee hs ote i ocal ersl,Bnnlnface
o i hmr a il nwye ademto nt i a ere
h i ees.
Frm oe o etrane o oregae,alh,t orede i oeral
"""

我们可以看到我们的Llama 3模型能够对新的提示进行推理并生成文本，尽管鉴于我们用于训练的训练数据量和迭代次数，输出似乎并不理想。我相信如果有更大规模的训练数据，我们将能够获得更好的准确性。

总结

Llama 3及其其他变体是当前LLM领域中最受欢迎的开源LLM。我相信从头开始构建Llama 3提供了构建许多新激动人心的基于LLM的应用所需的必要基础。