大型语言模型在战略和数学推理的准确性和可靠性方面面临挑战。为了解决这个问题，本文提出了 MCT Self-Refine (MCTSr) 算法，这是一种将大型语言模型（LLM）与蒙特卡洛树搜索（MCTS）相结合的创新算法，旨在提高复杂数学推理任务的性能。

该算法通过 “选择”、“自我完善”、“自我评估 ”和 “反向传播 ”的迭代过程来构建蒙特卡罗搜索树，并利用改进的置信度上限（UCB）公式来优化探索与开发之间的平衡。

主要贡献：

• 通过将 LLM与 UCT-MCTS 相结合，开发并验证了一种新型推理算法。作者增强了算法的关键组件，以更好地适应与 LLM的集成，并在奥林匹克级数学问题上证明了其有效性。
• 提出动态剪枝模块，在 MCTS 框架内完善决策过程，提高解决问题的效率和准确性。
• 广泛的实验深入揭示了 LLM 和 MCTS 的协同潜力，展示了在复杂推理任务中性能的提高
• 这项研究推动了 LLM 在复杂推理挑战中的应用。它为未来集成人工智能技术的创新奠定了基础，以增强 LLM 驱动型应用的决策能力、推理准确性和可靠性。

初步成果

蒙特卡洛树搜索（MCTS）

• 广泛应用于游戏和复杂决策过程的决策算法，通过建立搜索树和模拟结果来估计行动的价值。

MCTS 算法包括四个不同阶段：

1. 选择： 从根节点开始，算法根据特定策略（如 UCT）浏览有希望的子节点，直到到达叶节点。
2. 扩展： 在叶子节点上，除非代表博弈的终结状态，否则会添加一个或多个可行的新子节点，以说明未来可能的移动。
3. 模拟或评估： 从新添加的节点开始，算法进行随机模拟--通常称为 “滚动”--任意选择棋步，直到博弈结束，从而评估节点的潜力。
4. 反向传播： 模拟后，结果（胜、负或和）会传播回根节点，更新每个遍历节点的统计数据（如胜、负），为未来决策提供依据。

应用于树的置信度上限

• 该算法对 MCTS 中的选择阶段至关重要，它通过选择最大化的行动来平衡探索和利用：

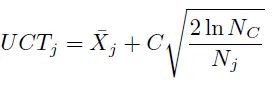
其中，¯Xj 是第 j 个行动的平均奖励，NC 是父节点的总访问次数，nj 是第 j 个节点的模拟访问次数，C 是平衡开发和探索的常数。

MCT 自我定义

• 算法是蒙特卡洛树搜索（MCTS）与大型语言模型的集成，将数学问题解决方案的迭代细化过程抽象为搜索树结构。
• 该算法的操作流程遵循 MCTS 算法的一般模式。
• 采用自我反思驱动的自我改进来完善答案；利用模型的自我奖励能力对不同答案版本的奖励进行采样。

方法论

MCTSr 工作流程

MCTSr 的工作流程概述如下，代理可以像人类一样从试错中学习决策和推理。

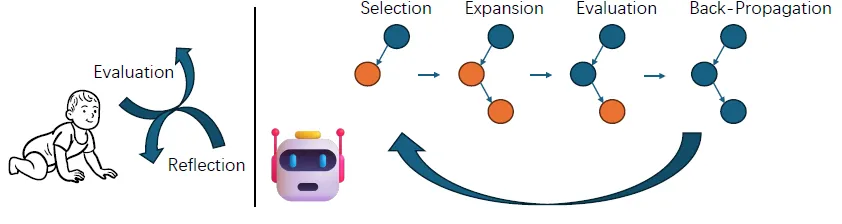
MCTSr 的主要工作流程如下：

• 初始化： 使用天真模型生成的答案和假回答（如 “我不知道”）建立根节点，以尽量减少模型的过拟合趋势。
• 选择： 该算法使用值函数 Q 对所有未完全展开的答案进行排序，并使用贪婪策略选择最高值节点进行进一步探索和完善。
• 自我定义： 选定的答案 a 将使用自我定义框架 [2] 进行优化。起初，模型会生成一个反馈 m，指导提炼过程以生成一个增强的答案 a′。
• 自我评价： 对改进后的答案进行评分，以采样奖励值并计算其 Q 值。这涉及模型自我奖励反馈和限制，如严格的评分标准和抑制满分，以确保评分的可靠性和公平性。
• 反向传播： 精炼答案的值会向后传播到其父节点和其他相关节点，以更新树的值信息。如果任何子节点的 Q 值发生变化，父节点的 Q 值也会随之更新。
• UCT 更新：更新所有节点的 Q 值后，我们将确定一个候选节点集合 C，以便进一步扩展或选择，然后使用 UCT 更新公式更新所有节点的 UCT 值，以便进入下一个选择阶段。

算法在这些阶段中不断迭代，直到满足终止条件 T，包括扩展限制或最大探索深度，不断改进答案质量，探索新的可能性。

自我定义

• 模型在多轮对话提炼提示的引导下，优化问题 P 的答案 a。
• 最初，模型会生成一个关于 a 的反思性或批判性评论 m。
• 随后，在 m 的指导下，模型对 a 进行修改，生成改进版本 a′。
• 这种迭代改进提高了答案的质量，利用结构化反馈推动答案的演变。

自我评价

• 在数学问题 P 的提炼过程中，答案 a 的 Q 值被定义为将 a 进一步提炼为更优答案的预期质量，这是因为从 a 到其改写形式的过渡具有马尔可夫性质。
• 与传统的 MCTS 不同，Q(s, a) 是对状态 s 中行动 a 的值的估计，而这里的 Q(a) 则来自对归属于 a 的奖励函数值的多次采样。
• 该模型利用自我奖励方法来估算 a 的奖励，要求它提供从 -100 到 100 的奖励分值。

为此，设计了三个约束条件：

(1) 提示约束： 模型在进行奖励评分时必须遵守最严格的标准。

(2) 满分抑制： 指示模型不得提供完整的反馈分数；任何超过 95 分的奖励都会以固定的数额减少，以抑制过高的分数。

(3) 重复采样： 每次访问搜索树节点时，我们都会对该节点的奖励进行重复采样，以提高自我评价的可靠性。需要注意的是，在对节点的子节点进行奖励采样时，我们也会对其父节点进行奖励采样，以增加奖励采样的样本量。

反向传播

• 在完成所有叶节点的奖励值采样和 Q 值更新后，我们会将这一变化传播到其父节点和祖节点。
• 在此更新过程中，如果节点 a 的子节点集合 Children(a) 中任何元素的 Q 函数值发生变化，则该节点的 Q 函数值将更新为

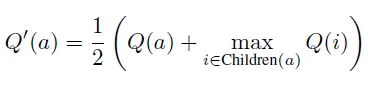
其中 Q′(a) 是答案 a 考虑其子节点影响的更新质量值，Q(a) 是仅考虑其奖励采样的朴素质量值，maxi∈Children(a) Q(i) 表示 a 的子节点中的最高质量值。

更新 UCT 和选择

更新树中所有节点的 Q 值后，我们进入下一轮选择的选择阶段。此过程包括以下步骤：

候选节点选择

• 重点选择所有叶节点和未完全扩展的节点，忽略细化路径的历史是可行的。
• 但考虑到在此任务中充当策略的大型语言模型 (LLM) 可以为任何答案状态 a 生成无限数量的细化动作 m，每个节点都可能面临一组无限的扩展动作
• 提出了两个判断“完全扩展”的标准：节点的子节点数量达到预定义的限制。并且，至少一个子节点的 Q 值超过节点的
• 根据这些标准确定候选节点集合C，以便进一步扩展或选择。

UCT 更新

• 借鉴 AlphaGo，我们使用 UCT 和 UCB-1 方法来平衡节点的探索和利用；对于候选集 C 中的节点 a，其 UCTa 值为，

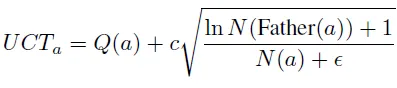
其中，Q(a) 是答案 a 的 Q 值，N(-) 是给定节点的总访问次数，c 是平衡开发和探索的常数，ϵ 是避免除以零的小常数。

排序和选择： 根据候选集 C 的 UCT 值，我们可以通过贪婪抽样或重要性抽样，选择一个最优节点进行探索提炼。

终止函数

搜索终止函数标准 T 可以从几个条件中衍生出来：

a) 提前终止： 当搜索结果的改善程度降低或连续搜索产生重复结果时，就会终止搜索。

b) 搜索限制： 一旦滚动次数达到预定限制，或者树中的一个或多个节点满足最大深度限制，搜索就会终止。

c) 基于语言模型 Logits 的高级标准： 搜索根据从语言模型对数中得出的预定指标得出结论。

一旦满足终止函数条件 T，我们就可以根据 Q 值或其他条件从树节点中收集最佳答案。

评估

为了评估 MCTSr 算法在解决数学问题方面的有效性，我们采用了 LLaMA3-8B （Meta AI，2024 年）作为基础模型，并用 MCTSr 进行了增强。

GSM 基准

• 在 GSM8K 和 GSM-hard 测试集上对上述方法进行了评估，这两个测试集分别涉及典型和具有挑战性的数学问题。
• 下表显示了 MCTSr 在 GSM 数据集上的性能

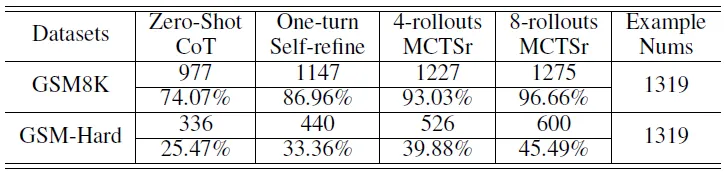
• 结果表明，MCTSr 的推出次数与成功率直接相关，随着迭代次数的增加，成功率显著提高，特别是在不太复杂的 GSM8K 中
• 复杂程度较高的 GSM-Hard 集即使迭代次数较多，也会出现性能上限，这表明当前的策略在应对复杂问题时存在局限性。
• 这项工作表明，该算法有能力提高解决问题的性能，并且在不同复杂度的问题上具有不同的功效。

MATH 基准

• 下表显示了 MCTSr 在 MATH 数据集上的性能

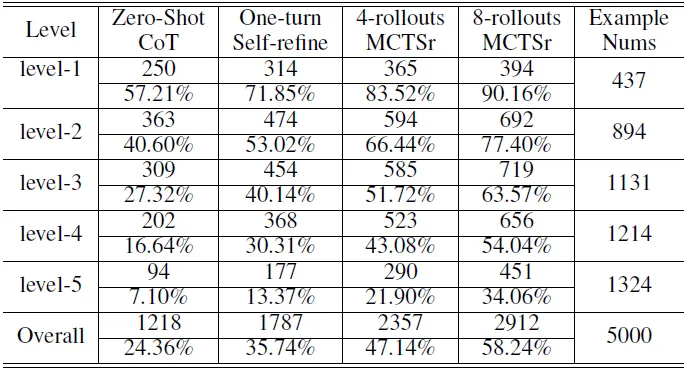
• 第 1 级结果显示了最高的成功率，8 次推广的 MCTSr 成功率高达 90.16%，解决了 437 个问题中的 394 个。随着推广次数的增加，这一级别的成功率也有了明显的提高
• 在最具挑战性的第 5 级部分，8 次滚动 MCTSr 配置的成功率为 34.06%，解决了 1324 个问题中的 451 个。这说明在高度复杂的情况下，算法的难度和性能都在不断增加
• 所有级别的总体性能显示，8 次滚动 MCTSr 的累计成功率为 58.24%，解决了 5000 个问题中的 2912 个。与 Zero-Shot CoT 最初 24.36% 的成功率相比，这一成功率有了大幅提高。

奥林匹克水平基准

以下结果显示了 MCTSr 在奥林匹克级数据集上的表现

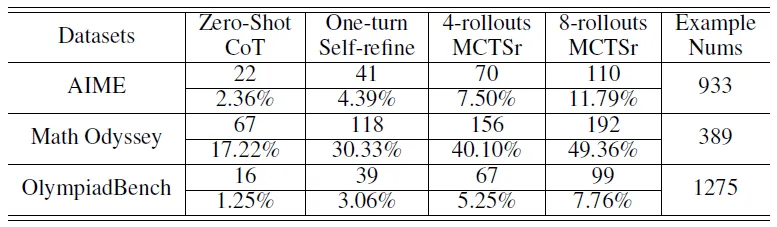
• AIME： 从 Zero-Shot CoT 的 2.36%（解决了 22 个问题）到 8rollouts MCTSr 的 11.79%（解决了 110 个问题）。
• GAIC Math Odyssey： 大幅提高，从 17.22%（解决 67 个问题）到 8 次滚动 MCTSr 的 49.36%（解决 192 个问题）。
• OlympiadBench： 从 Zero-Shot CoT 的 1.25%（解决了 16 个问题）提高到 8 次滚动 MCTSr 的 7.76%（解决了 99 个问题）。

局限性

• 作为一种通用决策框架，MCTSr 在各种场景中的潜在应用还有待进一步探索，例如黑盒优化问题和大型语言模型的自驱动配准。
• 此外，MCTSr 的组件具有很强的可扩展性，因此需要不断开发以确定和比较更广泛的组件算法，从而提高 MCTSr 算法的实用潜力和有效性。

结论

• 证明了蒙特卡洛树搜索（MCTSr）算法在提高大型语言模型（LLM）解决复杂数学问题的能力方面的有效性
• MCTSr 将蒙特卡洛树搜索（MCTS）与 LLM相结合，解决了在准确性和可靠性方面的关键挑战，特别是在数学推理任务中。
• 实验结果证实，在多个数据集上，问题解决的成功率有了显著提高，包括在奥林匹克级数学挑战中的出色表现