在探索最近邻分类器的基础上，让我们来看看它在回归领域的兄弟。最近邻回归器应用了相同的直观概念来预测连续值。但随着我们的数据集越来越大，有效地找到这些邻居变得非常困难。这就是 KD 树和 Ball 树的用武之地。

令人沮丧的是，没有明确的指南真正解释这些算法的工作原理。当然，有一些 2D 可视化，但它们通常无法清楚地说明树在多维环境中的工作原理。

在这里，我们将解释这些算法中实际发生的事情，而不使用过于简单的二维表示。我们将专注于树本身的构建，并看看哪些计算（和数字）真正重要。

定义

最近邻回归器是一种简单的预测模型，它通过对附近数据点的结果取平均值来估算值。该方法建立在相似输入可能产生相似输出的理念之上。

使用的数据集

为了说明我们的概念，我们将使用我们常用的数据集。该数据集有助于预测任何一天的高尔夫球手人数。它包括天气预报、温度、湿度和风况等因素。我们的目标是根据这些变量估计每日高尔夫球手的人数。

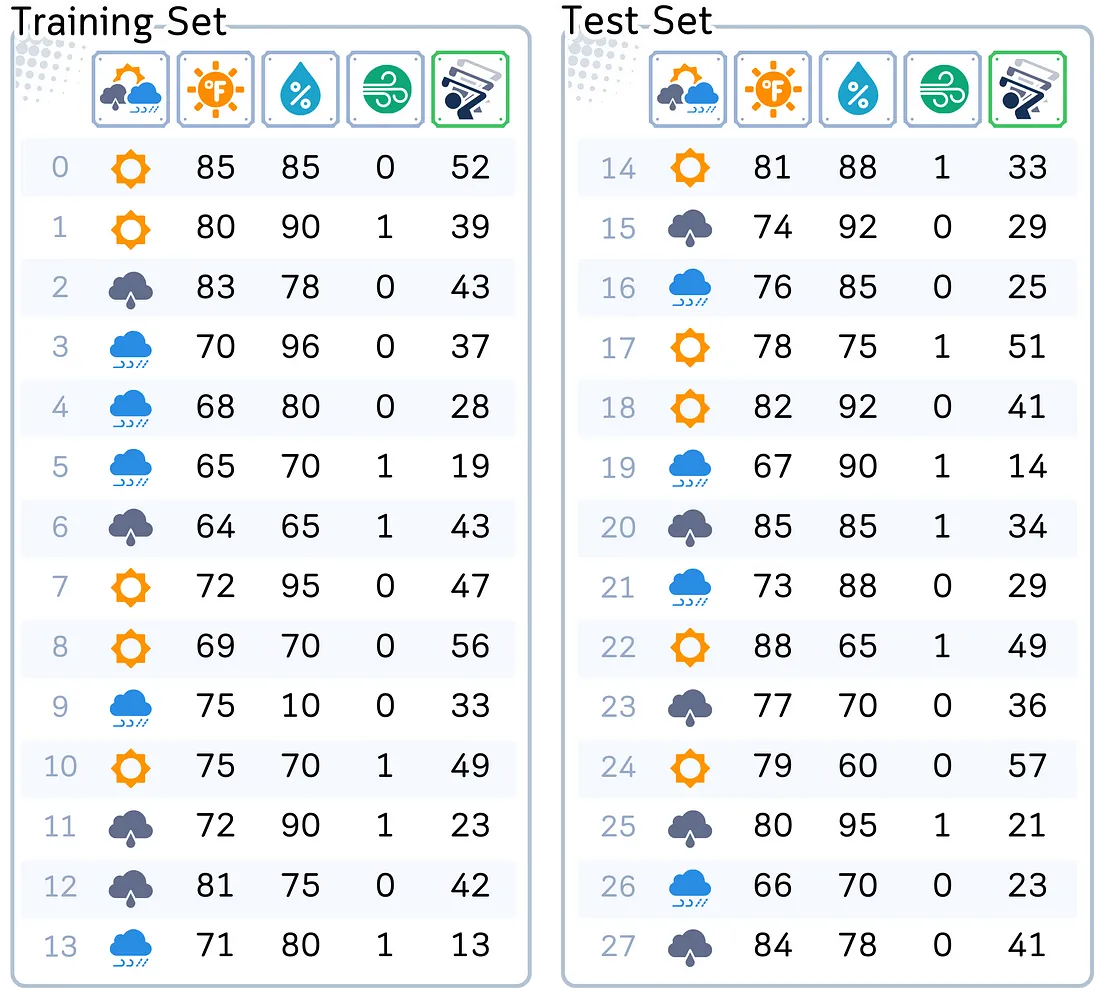
为了有效地使用最近邻回归，我们需要预处理数据。这涉及将分类变量转换为数字格式并缩放数字特征。

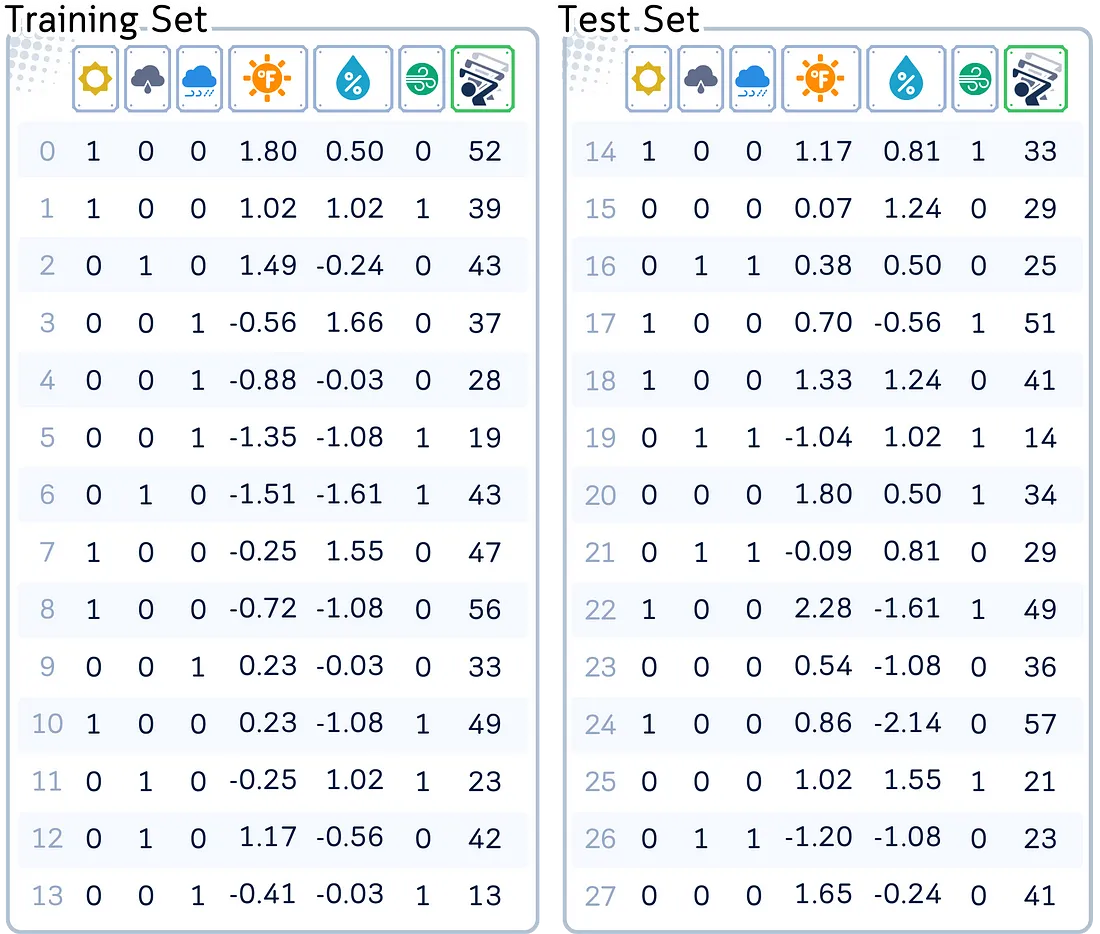
# Import libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
# Create dataset
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
df = pd.DataFrame(dataset_dict)
# One-hot encode 'Outlook' column
df = pd.get_dummies(df, columns=['Outlook'])
# Convert 'Wind' column to binary
df['Wind'] = df['Wind'].astype(int)
# Split data into features and target, then into training and test sets
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Identify numerical columns
numerical_columns = ['Temperature', 'Humidity']
# Create a ColumnTransformer to scale only numerical columns
ct = ColumnTransformer([
    ('scaler', StandardScaler(), numerical_columns)
], remainder='passthrough')
# Fit the ColumnTransformer on the training data and transform both training and test data
X_train_transformed = ct.fit_transform(X_train)
X_test_transformed = ct.transform(X_test)
# Convert the transformed data back to DataFrames
feature_names = numerical_columns + [col for col in X_train.columns if col not in numerical_columns]
X_train_scaled = pd.DataFrame(X_train_transformed, columns=feature_names, index=X_train.index)
X_test_scaled = pd.DataFrame(X_test_transformed, columns=feature_names, index=X_test.index)

主要机制

近邻回归器的工作原理与分类器类似，但它不是对一个类别进行投票，而是对目标值进行平均。基本过程如下：

1. 计算新数据点与训练集中所有点之间的距离。
2. 根据这些距离选择 K 个近邻。
3. 计算这 K 个邻居目标值的平均值。
4. 将此平均值作为新数据点的预测值。

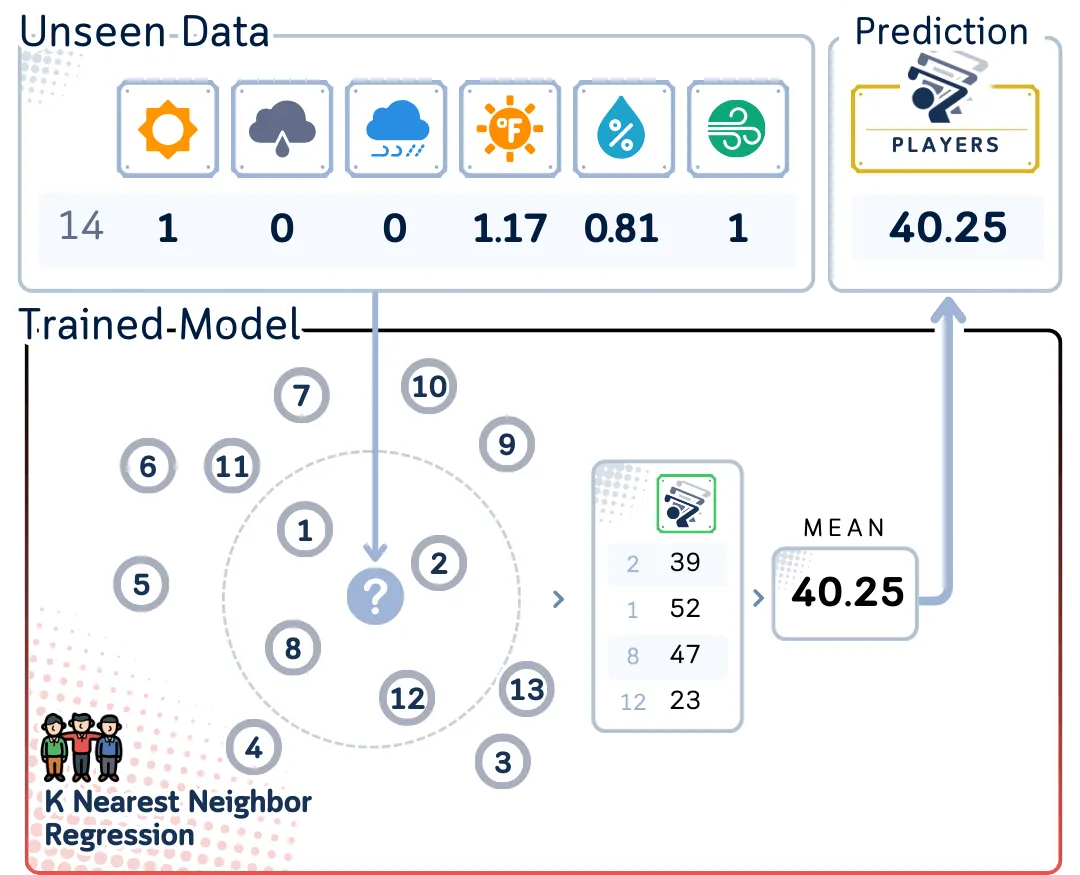
上述使用所有数据点查找邻居的方法被称为 “蛮力法”。这种方法简单明了，但对于大型数据集来说速度较慢。

用于 KNN 回归的 KD 树

KD 树（K 维树）是一种二叉树结构，用于组织 k 维空间中的点。它对多维数据中的近邻搜索和范围搜索等任务特别有用。

训练步骤

1. 构建 KD 树：

a. 从包含所有点的根节点开始。

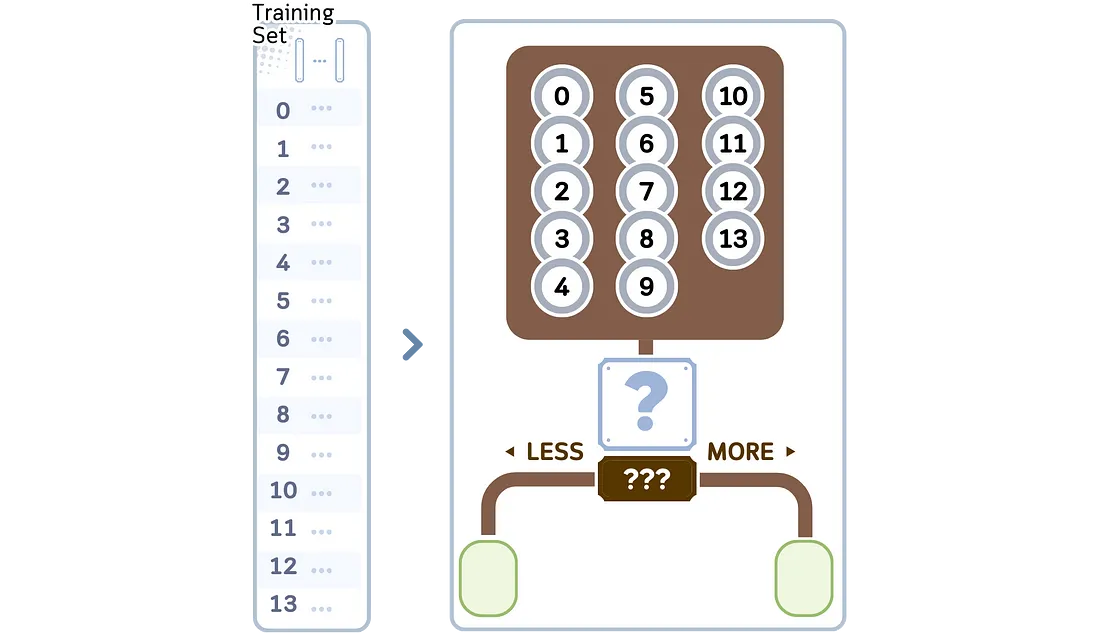
b. 选择要分割的特征。其实任何随机特征都可以，但另一个好方法是看哪个特征的中值最接近最大值和最小值的中点。

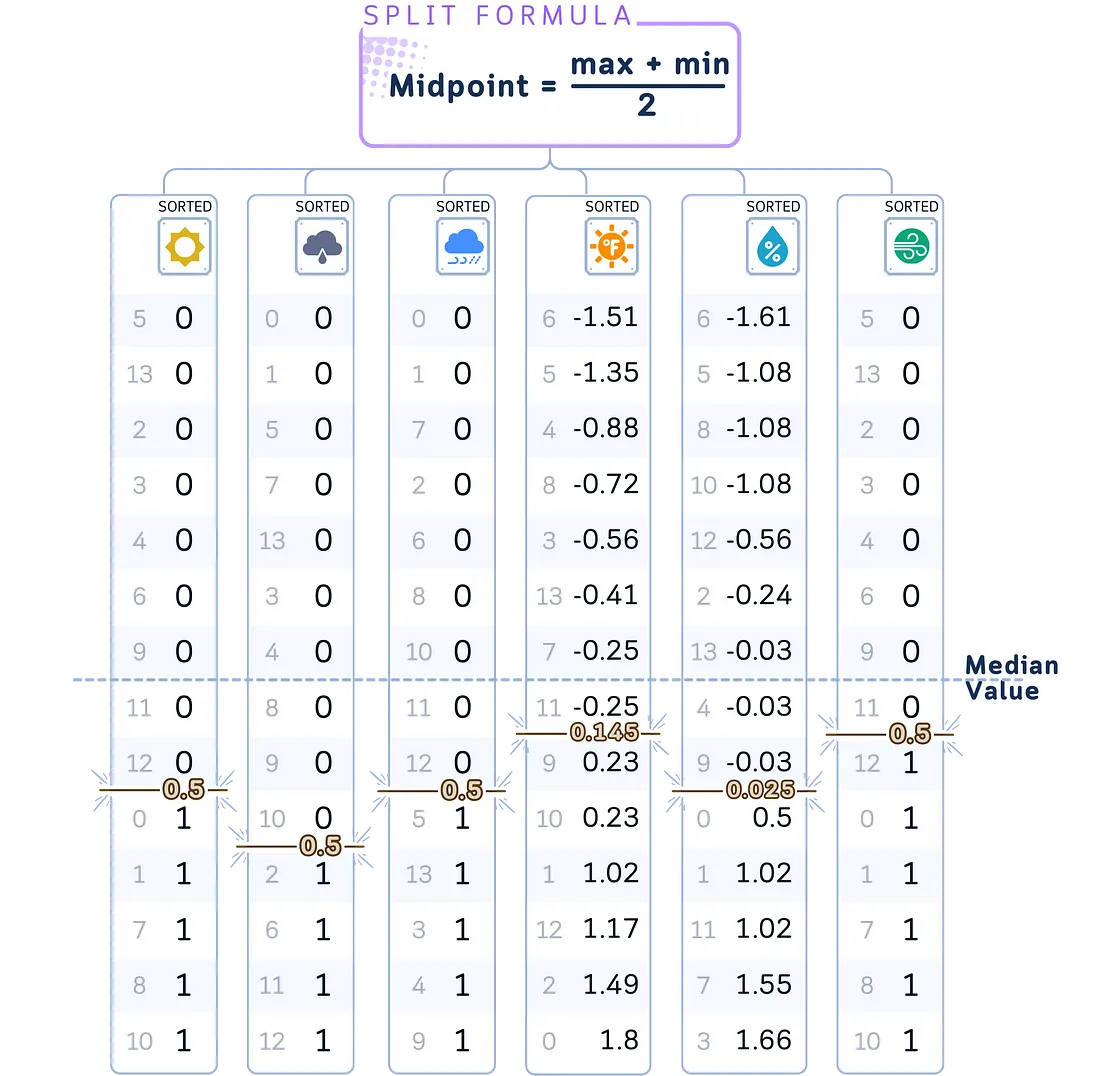
c. 在选定的特征点和中点分割树。

d. 递归执行 a-c 步骤，直到达到停止标准，通常是最小叶片大小。

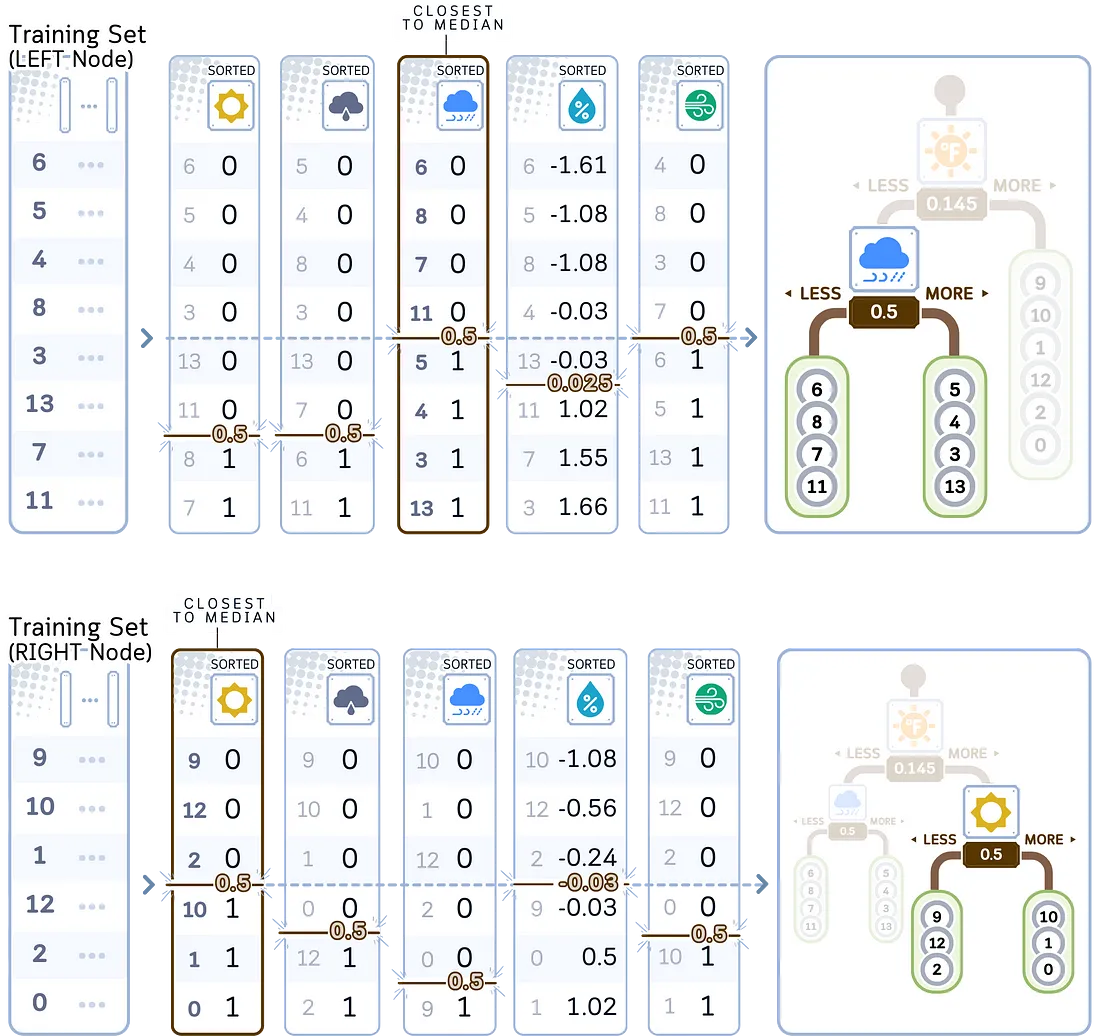
2. 存储目标值：

与 KD 树中的每个点一起，存储其相应的目标值。每个节点的最小值和最大值也会被存储起来。

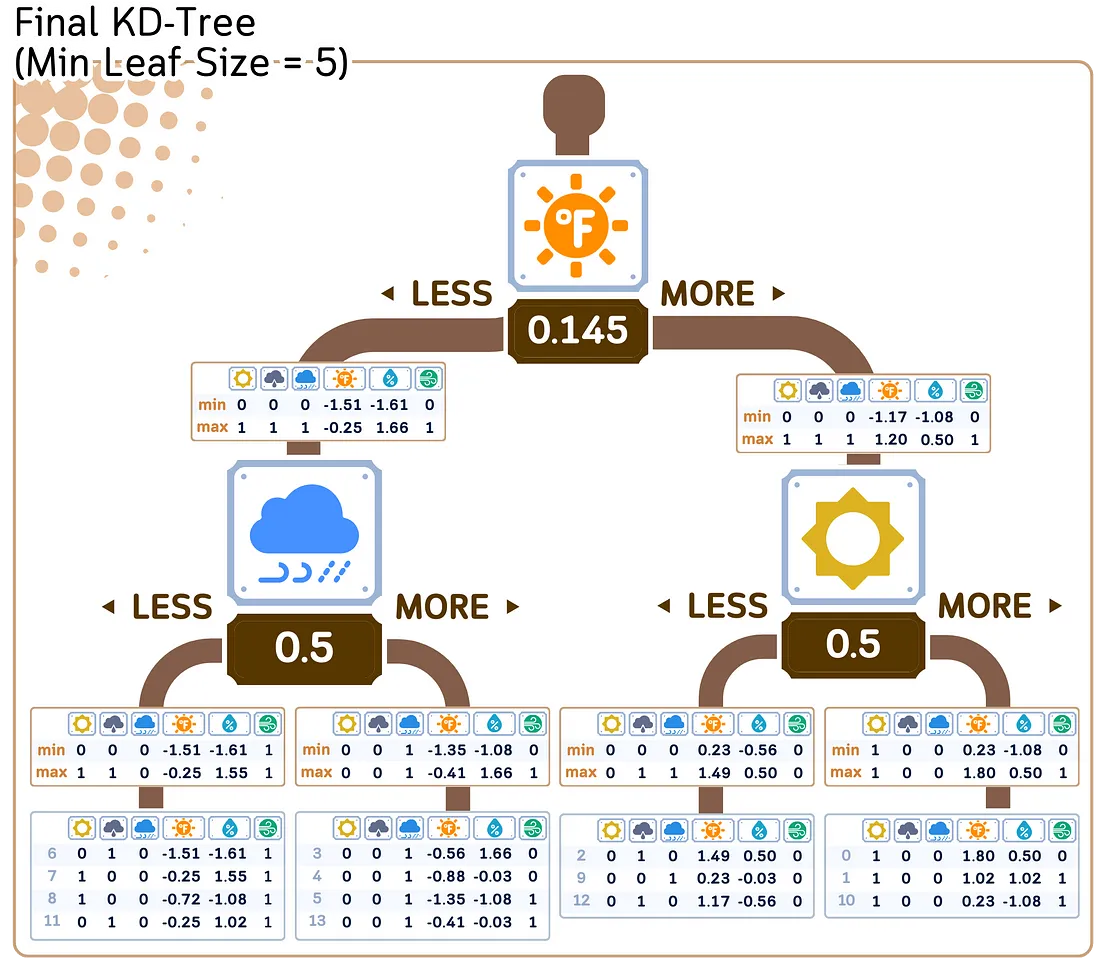
回归/预测步骤：

1. 遍历 KD 树：

a. 从根节点开始。

b. 将查询点（测试点）与每个节点上的分割维度和值进行比较。

c. 根据比较结果向左或向右递归遍历。

d. 到达叶节点时，将其点添加到候选集。

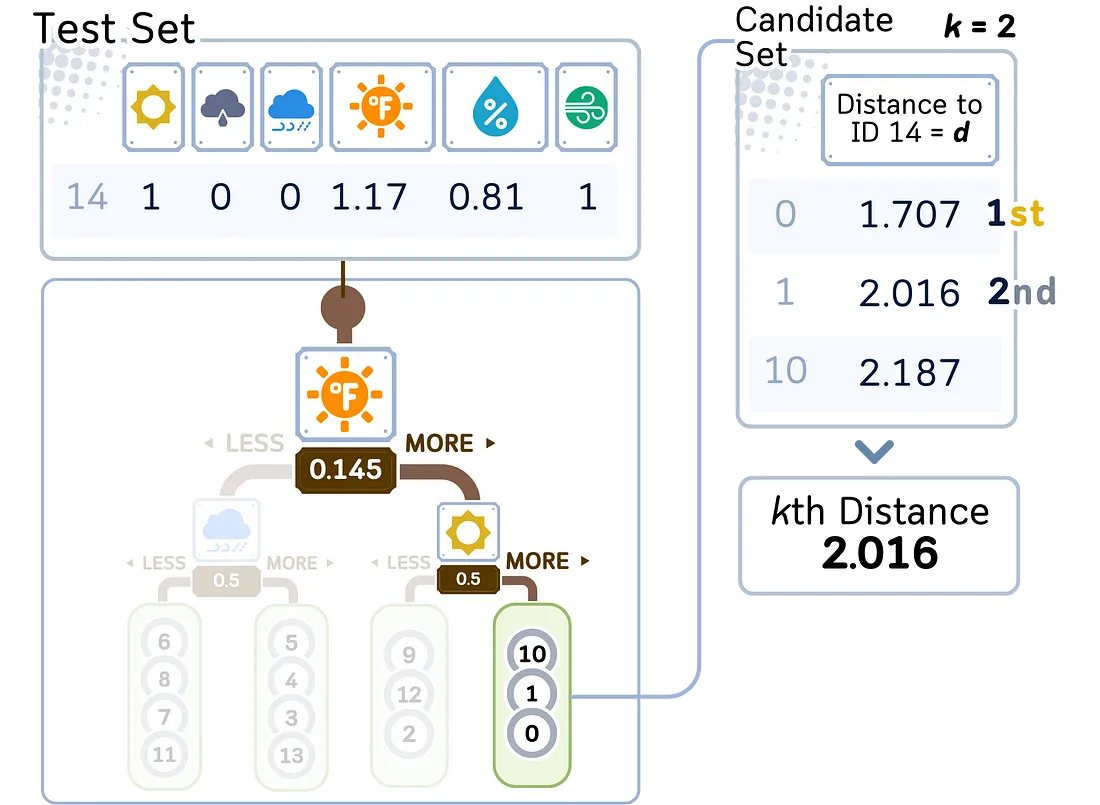
2. 完善搜索：

a. 在树中回溯，检查其他分支中是否有更接近的点。

b. 使用距离计算法计算未探索分支的最大值和最小值，以确定是否有必要进行探索。

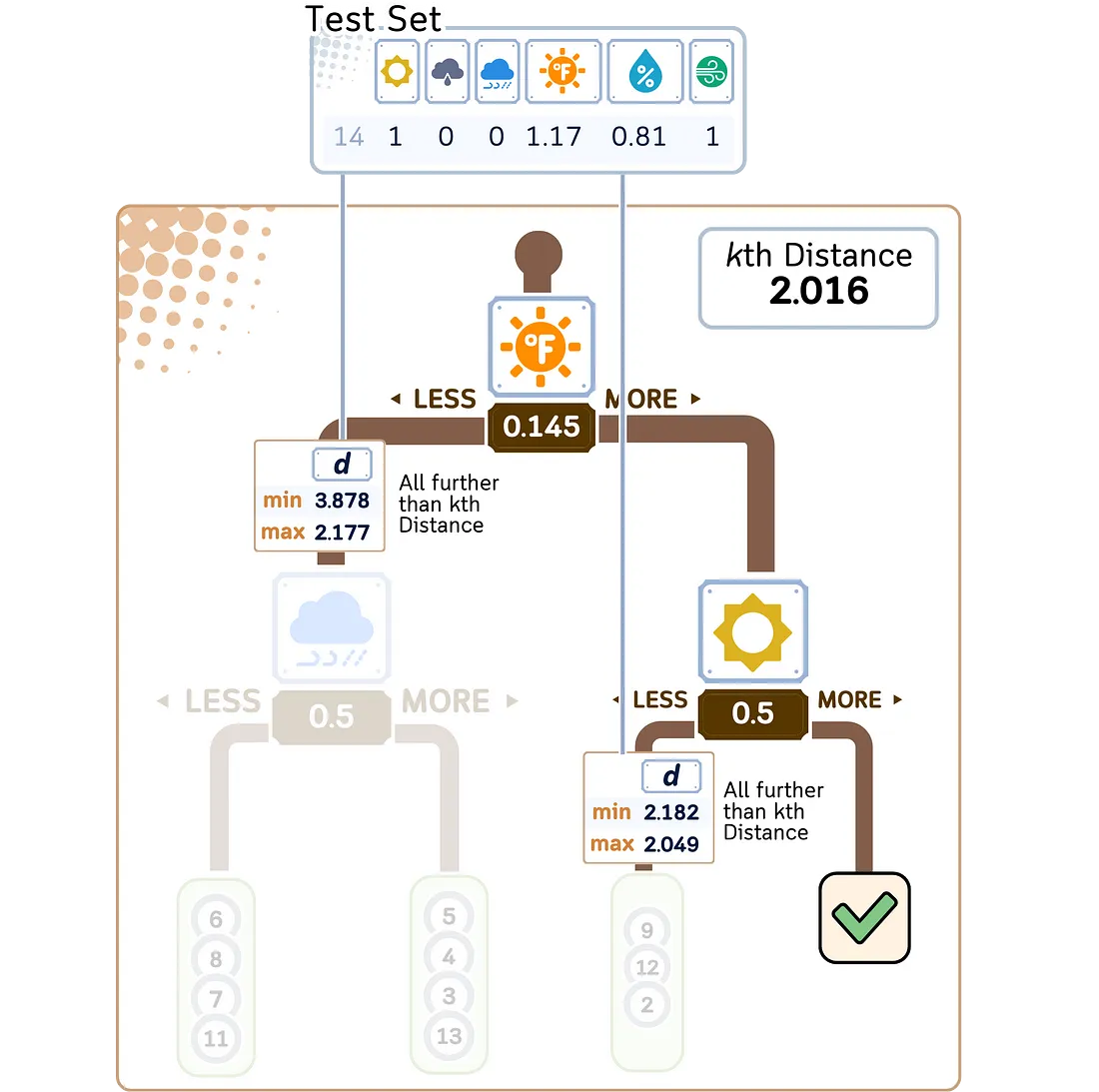
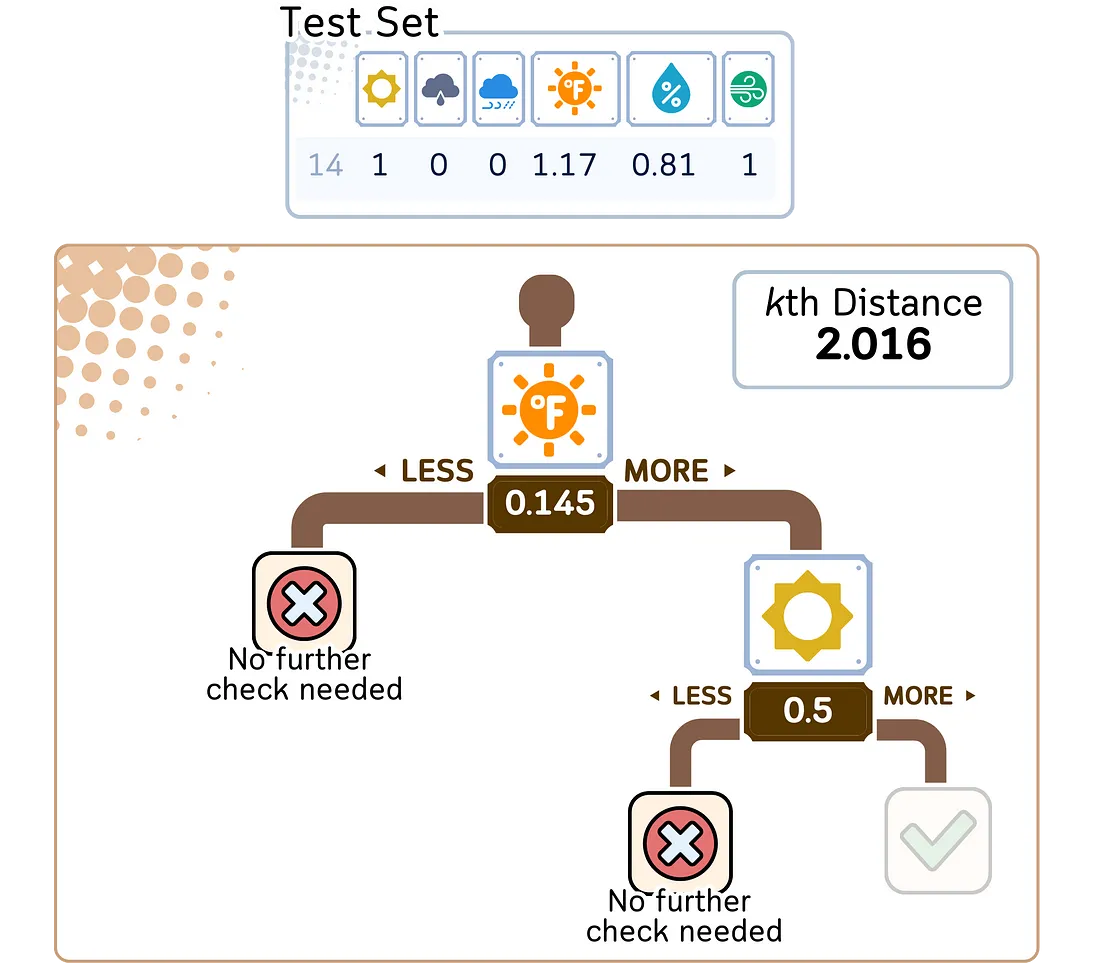
3. 找出 K 个最近的邻居：

a. 在找到的候选点中，选择离查询点最近的 K 个点。

4. 进行回归

a. 计算 K 个近邻点目标值的平均值。

b. 这个平均值就是查询点的预测值。

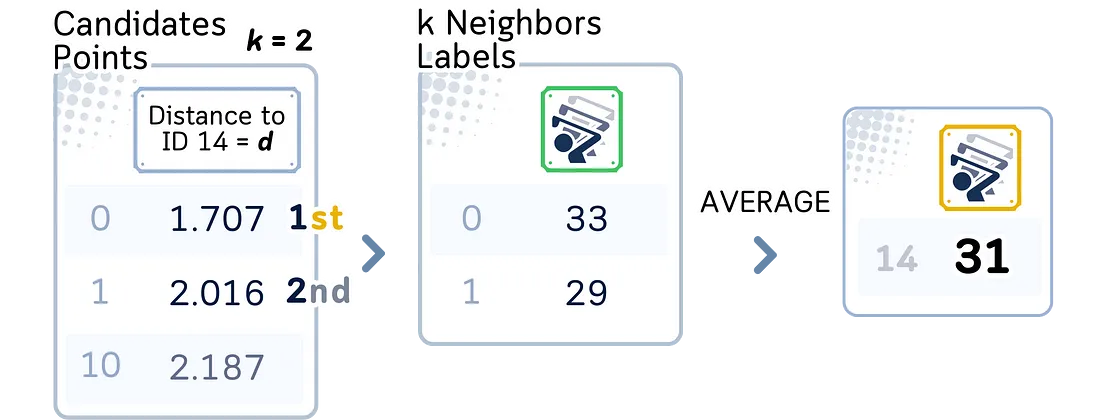
通过使用 KD 树，在许多情况下，寻找近邻的平均时间复杂度可以从蛮力法的 O(n) 降低到 O(log n)，其中 n 是数据集中的点数。这使得 KNN 回归在处理大型数据集时更加高效。

用于 KNN 回归的球树

球树是另一种空间分区数据结构，它将点组织在一系列嵌套的超球中。它对高维数据特别有效，在高维数据中，KD 树的效率可能会降低。

训练步骤：

1. 构建球树

a. 计算节点中所有点的中心点（平均值）。这就是支点。

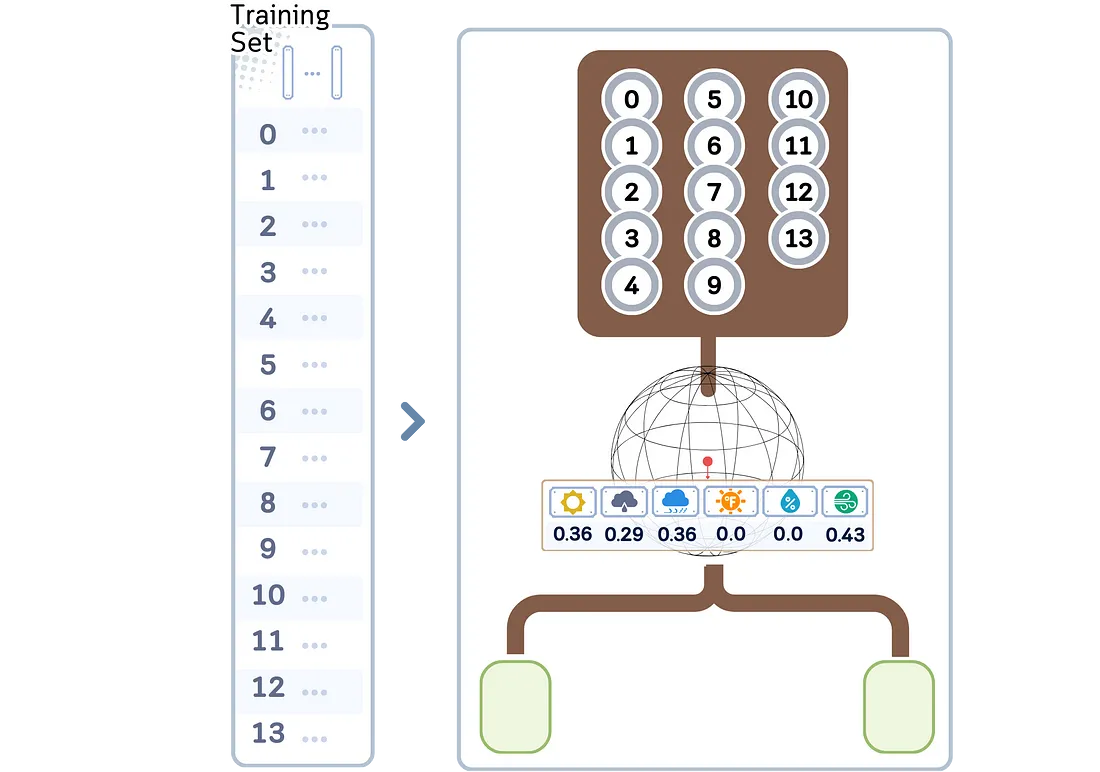
b. 制作第一个分支：

- 找到第一个中心点： 选择离支点最远的点作为第一个圆心，以其距离为半径。

- 找到第二个中心： 从第一个中心点出发，选择最远的点作为第二个中心点。

- 分割： 将剩余的点划分为两个子节点，具体划分依据是它们离哪个中心点更近。

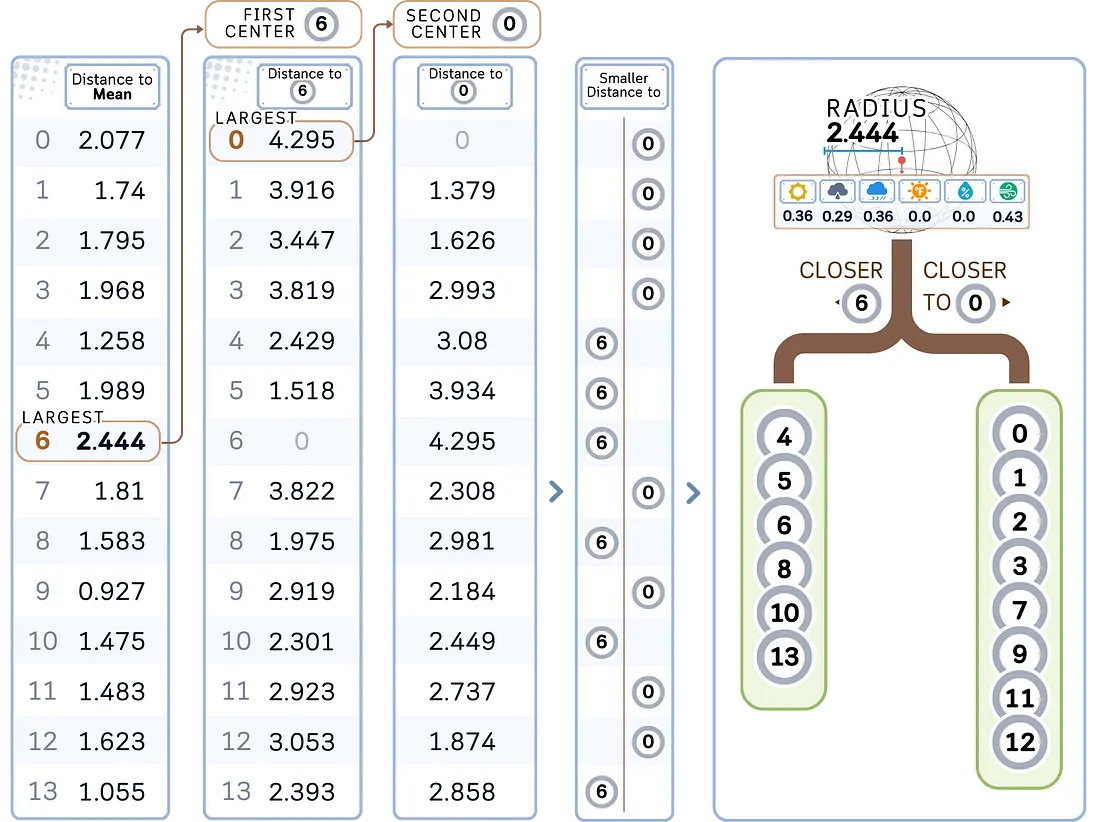
d. 对每个子节点递归应用 a-b 步骤，直到满足停止标准，通常是最小叶片大小。

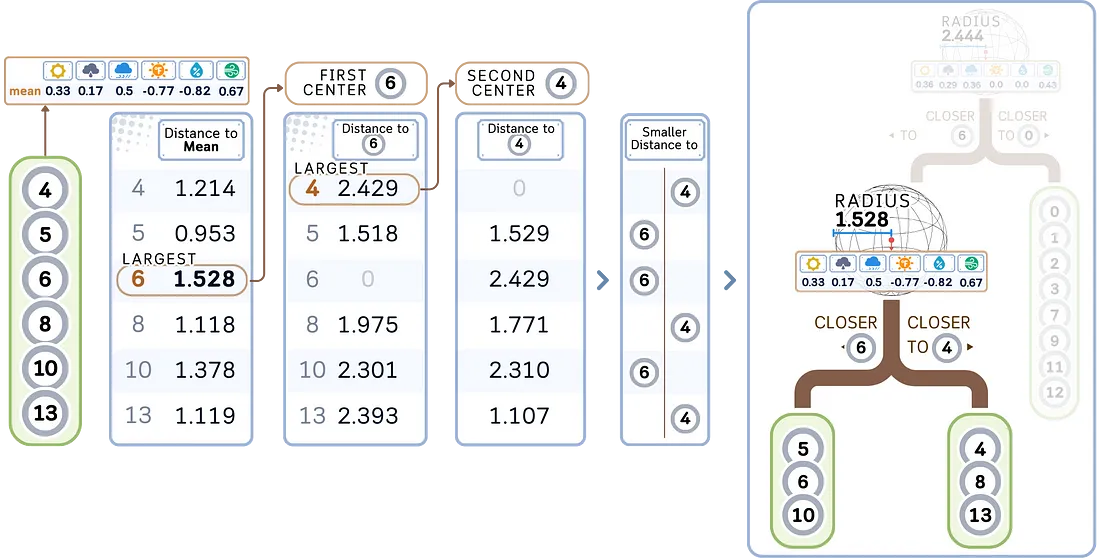
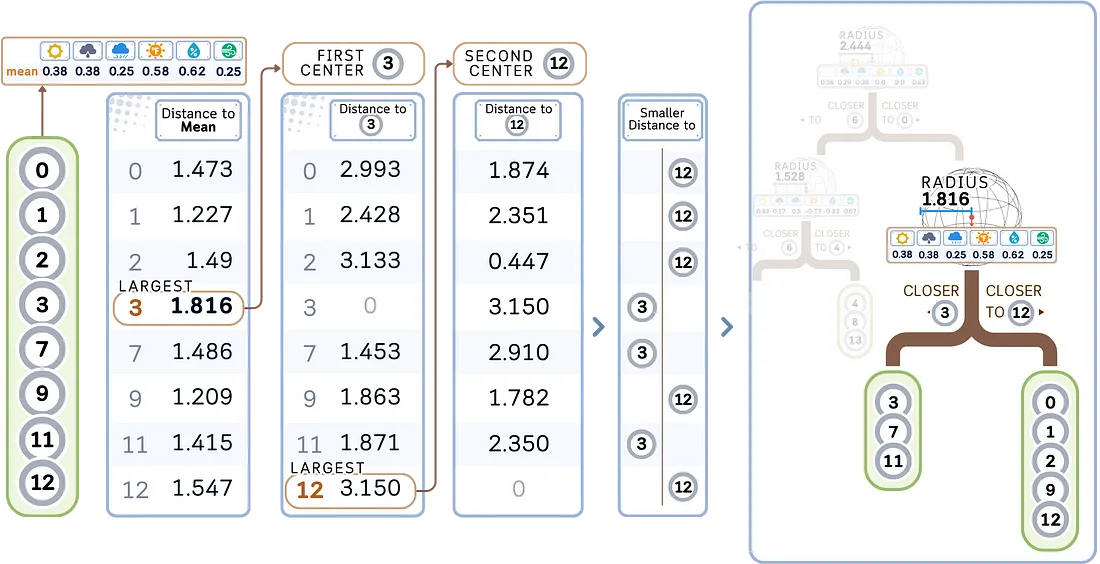
2. 存储目标值：

球形树中的每个点都会存储相应的目标值。每个节点的半径和中心点也会被存储起来。

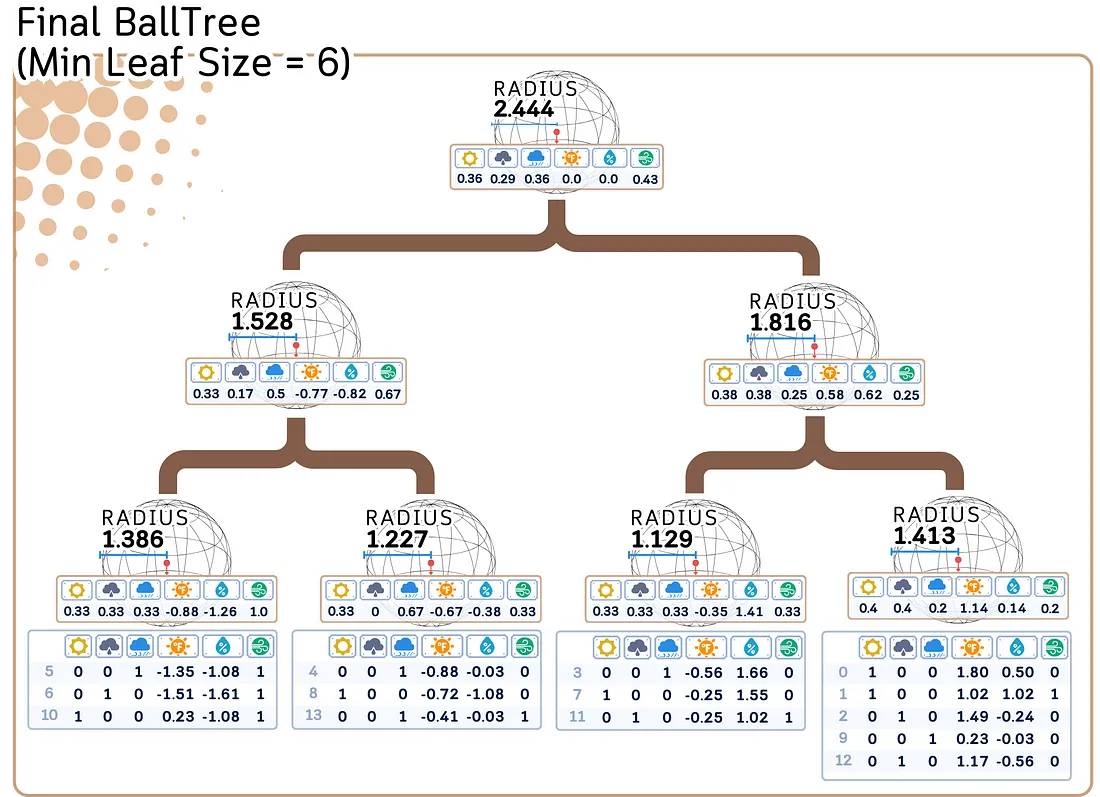
回归/预测步骤：

1. 遍历球树：

a. 从根节点开始

b. 在每个节点，计算未见数据与每个子超球中心之间的距离。

c. 先进入最近的超球。

d. 到达叶节点时，将其点添加到候选集。

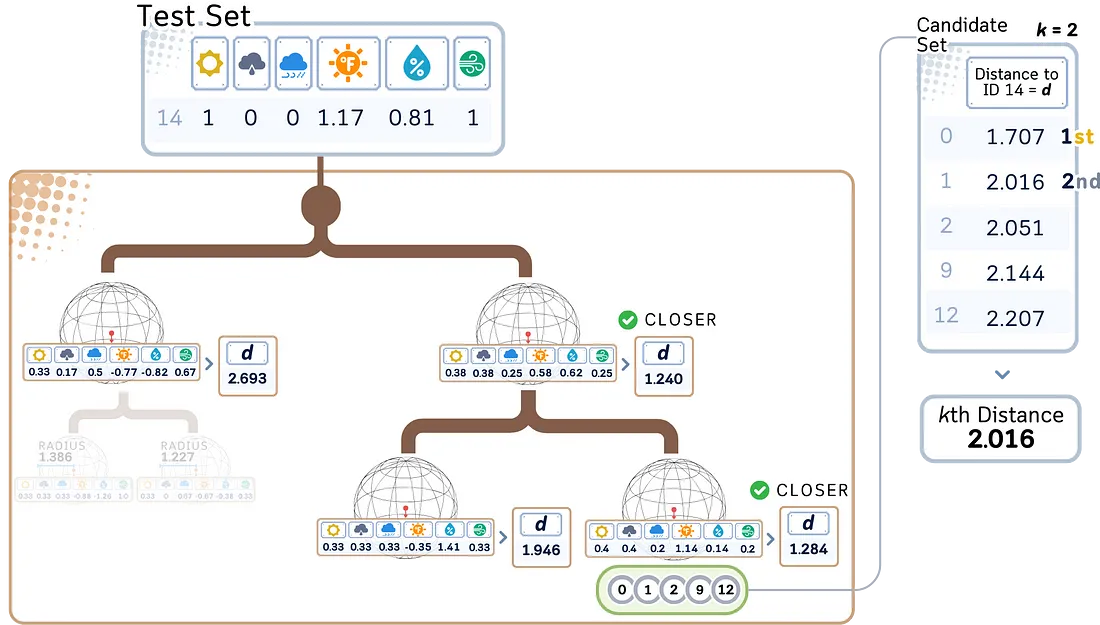
2. 完善搜索：

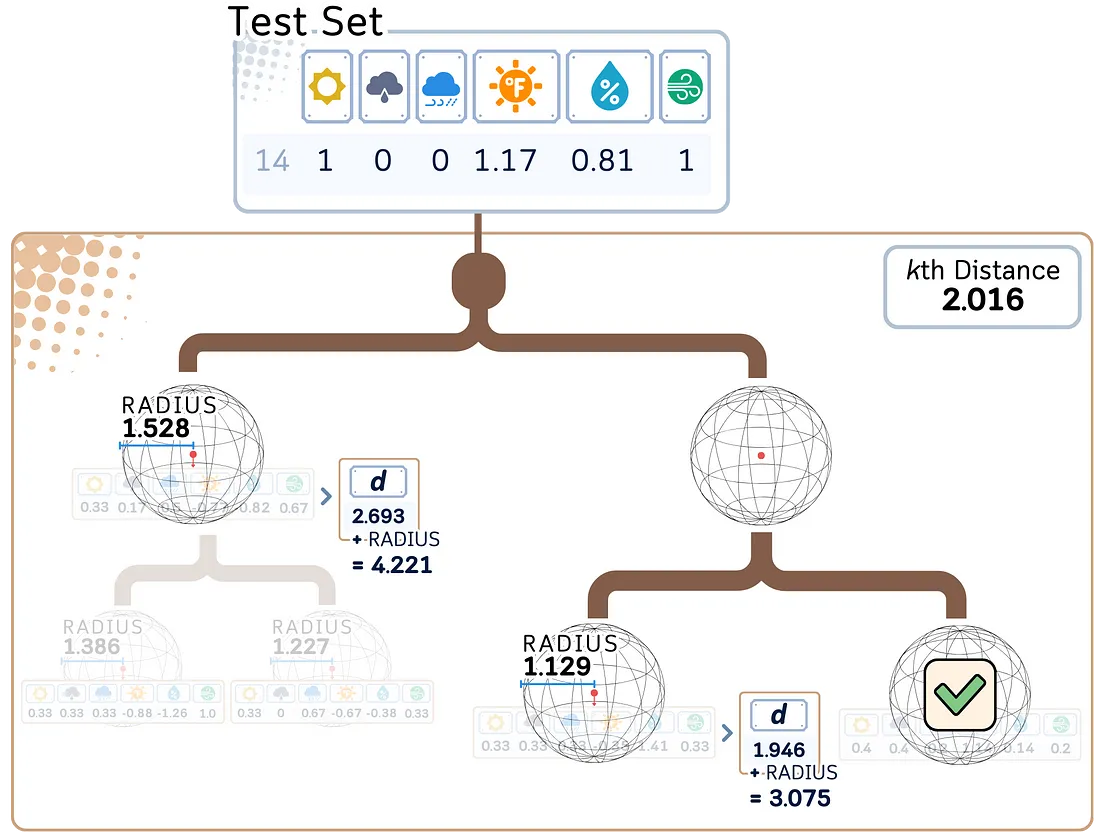
a. 确定是否需要探索其他分支。

b. 如果到一个超球的距离加上它的半径大于当前第 K 个最近距离，则可以安全地忽略该分支。

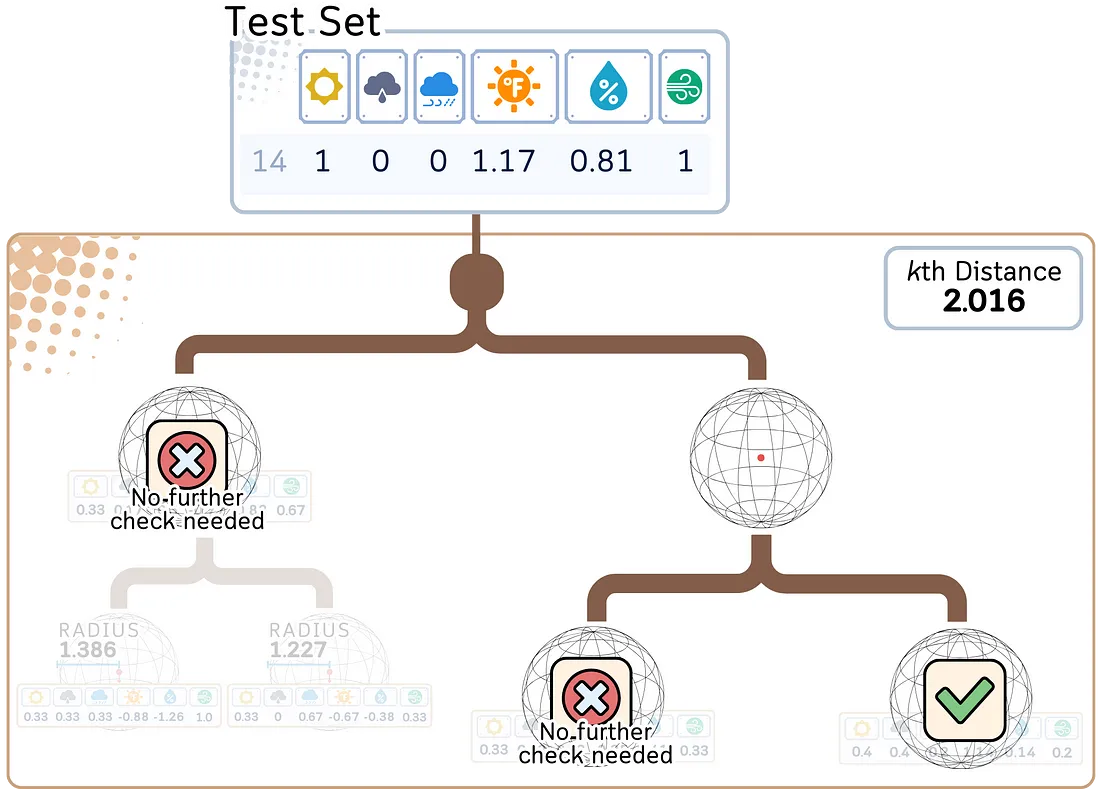
3. 找出 K 个最近的邻居：

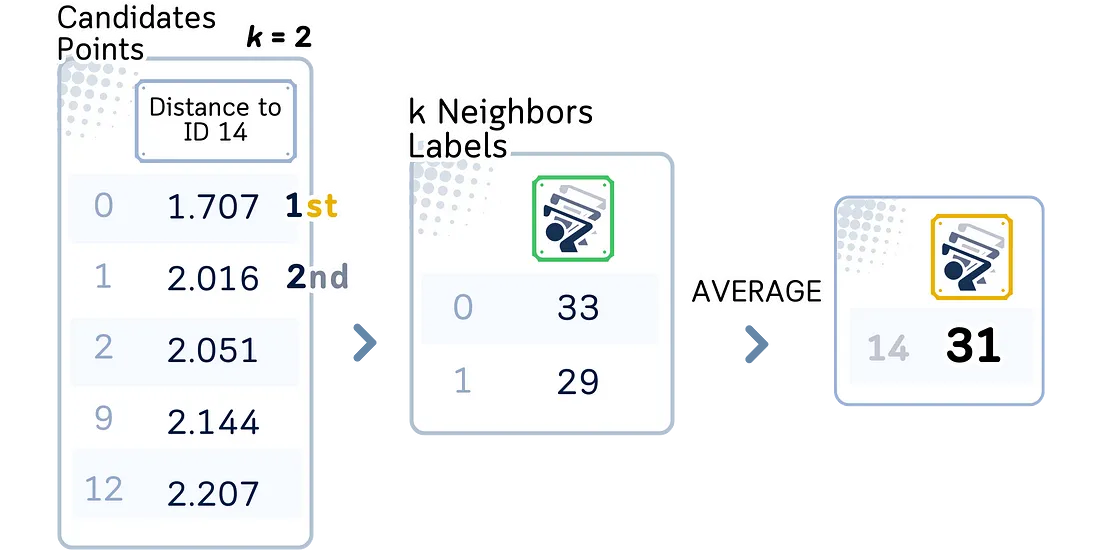
a. 在找到的候选点中，选择离查询点最近的 K 个点。

4. 进行回归：

a. 计算 K 个近邻点目标值的平均值。

b. 这个平均值就是查询点的预测值。

对于高维数据或当维度大于样本数的对数时，球树比 KD 树更有效。即使维数增加，球树也能保持良好的性能，因此适用于各种数据集。

球形树查询的时间复杂度平均为 O(log n)，与 KD 树类似，但球形树在维度较高的情况下通常表现更好，而 KD 树可能会降低到线性时间复杂度。

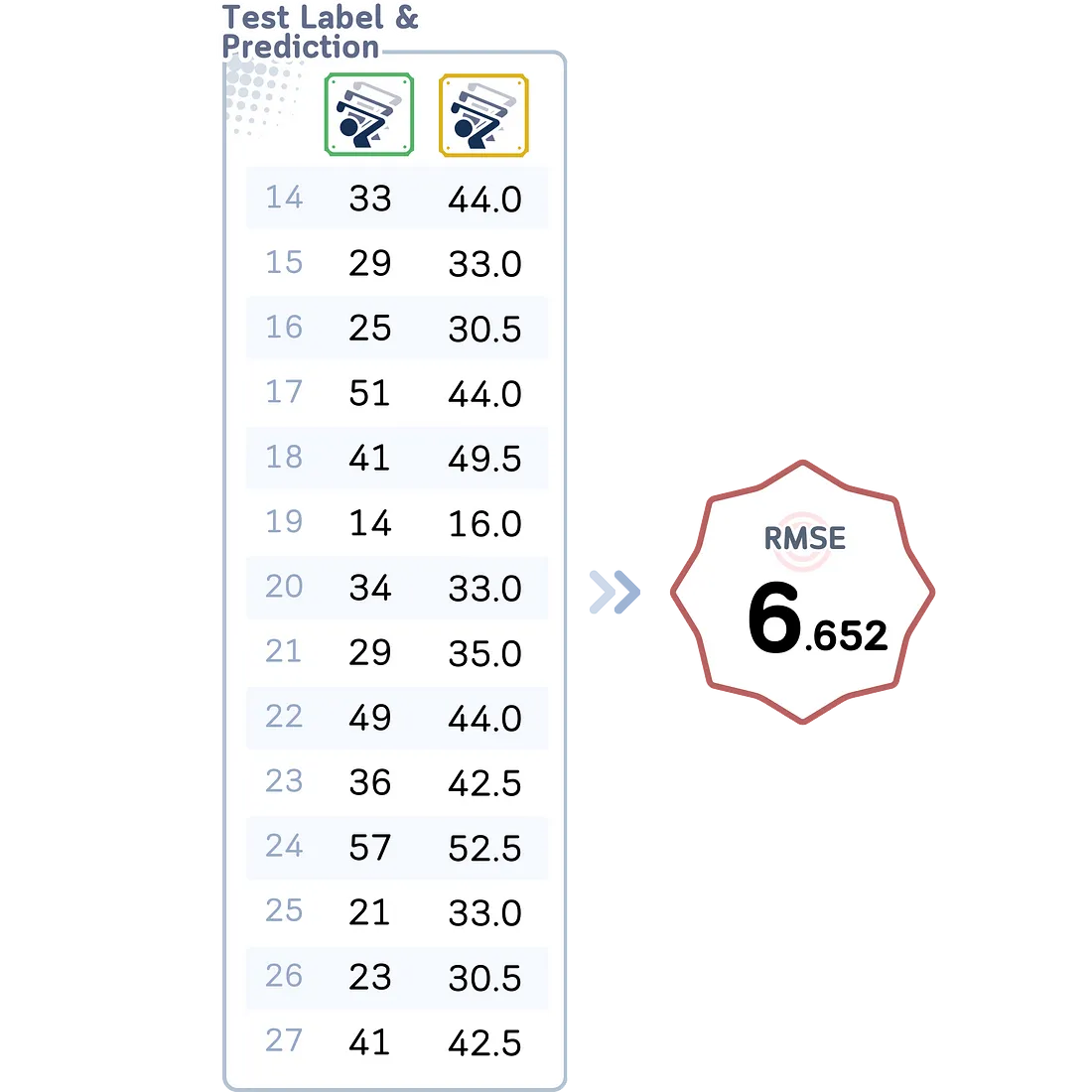
评估步骤（蛮力、KD 树、球树）

无论我们选择哪种算法，都会得到以下相同的结果：

选择哪种算法？

你可以遵循这个简单的规则来选择最佳算法：

- 对于小数据集（小于 1000 个样本），“brute ”算法可能足够快，并能保证找到精确的近邻。

- 对于特征较少的大型数据集（< 20 个），“kd_tree ”通常是最快的。

- 对于特征较多的大型数据集，“ball_tree ”通常表现最佳。

scikit-learn 中的 “auto ”选项通常如下图所示：

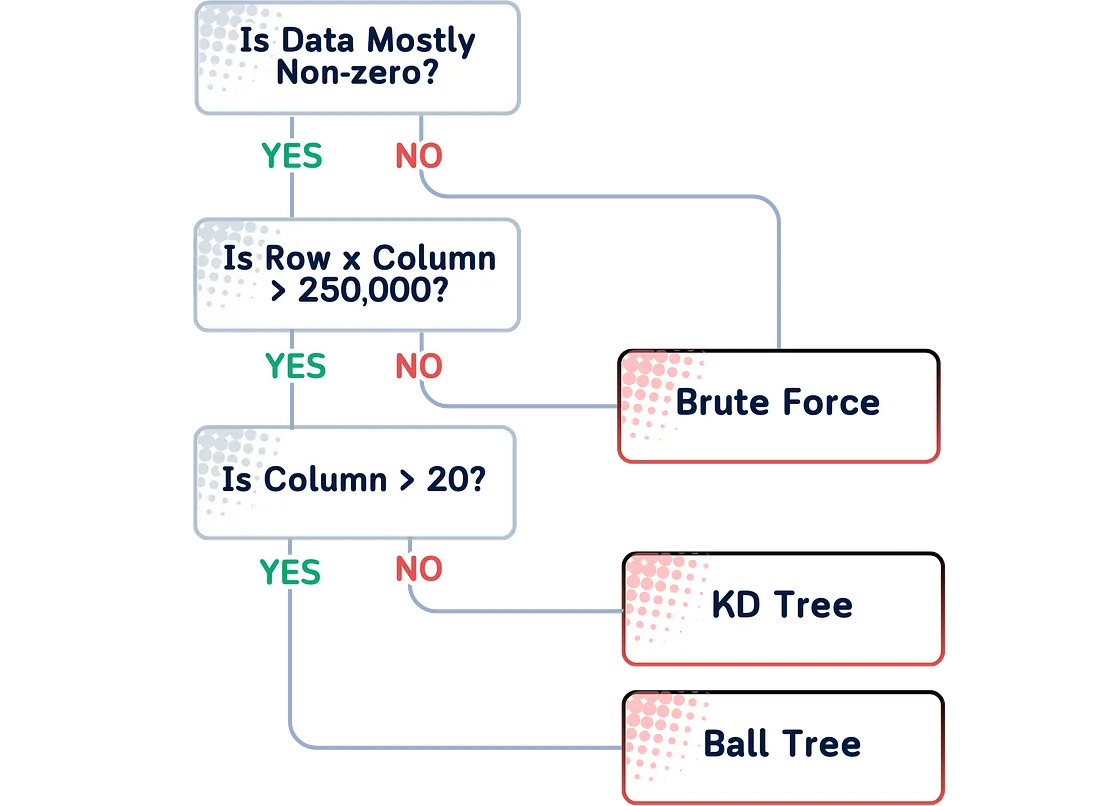
关键参数

虽然 KNN 回归有很多其他参数，但除了我们刚才讨论的算法（蛮力算法、KD 树、球树）之外，你主要需要考虑的是：

1. 邻居数 (K)。

- 较小的 K：对局部模式更敏感，但可能导致过度拟合。

- 较大的 K：预测更平滑，但可能会错过重要的局部变化。

与分类法不同的是，在回归法中，偶数也可以，因为我们是在求平均值。

2. 叶片大小

这是构建 KD 树或球树的停止条件。一般来说，它会影响构建和查询的速度，以及存储树所需的内存。

总结

K-Nearest Neighbors (KNN) 回归器是机器学习中一个基本但强大的工具。其简单明了的方法非常适合初学者，而其灵活性也确保了它对专家也非常有用。

在学习更多数据分析知识时，可以先使用 KNN 了解回归的基础知识，然后再探索更高级的方法。通过掌握 KNN 和计算近邻的方法，你将为应对数据分析中更复杂的挑战打下坚实的基础。

k 近邻回归码汇总

# Import libraries
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
from sklearn.neighbors import KNeighborsRegressor
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
# Create dataset
dataset_dict = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temperature': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0, 72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0, 88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
    'Humidity': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0, 90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0, 65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
df = pd.DataFrame(dataset_dict)
# One-hot encode 'Outlook' column
df = pd.get_dummies(df, columns=['Outlook'])
# Convert 'Wind' column to binary
df['Wind'] = df['Wind'].astype(int)
# Split data into features and target, then into training and test sets
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Identify numerical columns
numerical_columns = ['Temperature', 'Humidity']
# Create a ColumnTransformer to scale only numerical columns
ct = ColumnTransformer([
    ('scaler', StandardScaler(), numerical_columns)
], remainder='passthrough')
# Fit the ColumnTransformer on the training data and transform both training and test data
X_train_transformed = ct.fit_transform(X_train)
X_test_transformed = ct.transform(X_test)
# Convert the transformed data back to DataFrames
feature_names = numerical_columns + [col for col in X_train.columns if col not in numerical_columns]
X_train_scaled = pd.DataFrame(X_train_transformed, columns=feature_names, index=X_train.index)
X_test_scaled = pd.DataFrame(X_test_transformed, columns=feature_names, index=X_test.index)
# Initialize and train KNN Regressor
knn = KNeighborsRegressor(n_neighbors=5, 
                          algorithm='kd_tree', #'ball_tree', 'brute'
                          leaf_size=5) #default is 30
knn.fit(X_train_scaled, y_train)
# Make predictions
y_pred = knn.predict(X_test_scaled)
# Calculate and print RMSE
rmse = root_mean_squared_error(y_test, y_pred)
print(f"RMSE: {rmse:.4f}")