PCA（原理成分分析）通常用于数据科学，一般用于降维（通常也用于可视化），但实际上它对离群值检测也非常有用，本文将对此进行介绍。

PCA 背后的理念是，大多数数据集的某些列的方差远大于其他列，而且特征之间也存在相关性。这意味着：要表示数据，通常不需要使用尽可能多的特征；我们通常可以使用较少的特征--有时少得多--就能很好地近似数据。例如，对于一张包含 100 个特征的数字数据表，我们可能只需使用 30 或 40 个特征就能很好地表示数据，可能更少，也可能少得多。

为此，PCA 将数据转换为不同的坐标系，其中的维度被称为成分。

考虑到我们在异常值检测中经常遇到的维数灾难问题，使用较少的特征可能会非常有益。如在“用于异常值检测的共享最近邻和距离度量学习”中所述，使用许多特征会使异常值检测变得不可靠；高维数据的问题之一是它会导致点之间的距离计算不可靠（许多异常值检测器都依赖于此）。PCA 可以减轻这些影响。

此外，令人惊讶的是，使用 PCA 往往会使异常值更容易被检测到。PCA 变换通常会重塑数据，从而更容易识别异常点。

下面就是一个例子。

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
# Create two arrays of 100 random values, with high correlation between them
x_data = np.random.random(100) 
y_data = np.random.random(100) / 10.0
# Create a dataframe with this data plus two additional points
data = pd.DataFrame({'A': x_data, 'B': x_data + y_data}) 
data= pd.concat([data, 
   pd.DataFrame([[1.8, 1.8], [0.5, 0.1]], columns=['A', 'B'])])
# Use PCA to transform the data to another 2D space
pca = PCA(n_components=2) 
pca.fit(data)
print(pca.explained_variance_ratio_)
# Create a dataframe with the PCA-transformed data
new_data = pd.DataFrame(pca.transform(data), columns=['0', '1'])

首先创建原始数据，如左窗格所示。然后使用 PCA 对其进行转换。转换完成后，我们就得到了新空间中的数据，如右侧窗格所示。

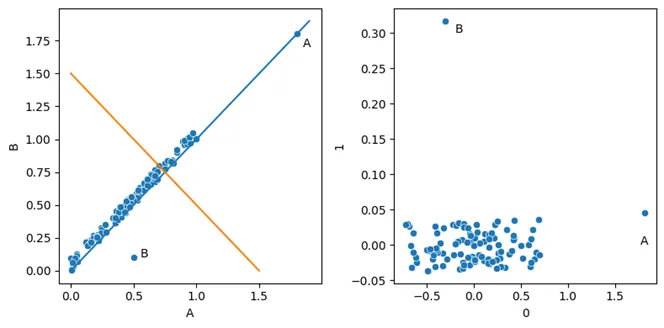
在这里，我创建了一个简单的合成数据集，数据高度相关。其中有两个异常值，一个是遵循一般模式但极端的异常值（A 点），另一个是每个维度都有典型值但不遵循一般模式的异常值（B 点）。

然后，我们使用 scikit-learn 的 PCA 类对数据进行转换。转换后的输出被放入另一个 pandas 数据框中，然后可以绘制（如图所示）或检查异常值。

从原始数据来看，数据往往沿着对角线排列。从左下角到右上角画一条线（图中的蓝线），我们就可以创建一个新的单一维度，很好地表示数据。事实上，在执行 PCA 时，这将是第一分量，而与之正交的直线（橙色线，也显示在左侧窗格中）则是第二分量，代表剩余的方差。

在更现实的数据中，我们不会有如此强烈的线性关系，但我们几乎总能在特征之间找到一些关联--完全独立的特征是很少见的。因此，PCA 通常是降低数据集维度的有效方法。也就是说，虽然通常有必要使用所有成分来完整描述每个项目，但只使用部分成分通常也能很好地描述每条记录（或几乎每条记录）。

右侧窗格显示的是 PCA 变换所创建的新空间中的数据，X 轴为第一分量（捕捉大部分方差），Y 轴为第二分量（捕捉剩余方差）。对于二维数据，PCA 变换只是对数据进行旋转和拉伸。在更高维度中，这种变换更难可视化，但效果类似。

打印解释方差（上面的代码中包含一个打印语句来显示）表明，成分 0 包含 0.99 的方差，成分 1 包含 0.01 的方差，这与绘图结果非常吻合。

通常情况下，我们会一个一个地查看成分（例如，以直方图的形式），但在本例中，我们使用了散点图，这样可以同时查看两个成分，节省了空间。离群值作为两个成分中的极端值非常突出。

再仔细观察一下 PCA 的工作原理，它首先通过数据找到一条最能描述数据的线。在这条直线上，所有点与直线的平方距离都最小。这就是第一分量。然后，这个过程会找到一条与之正交的线，这条线能最好地捕捉剩余的方差。本数据集仅包含两个维度，因此第二个分量的方向只有一个选择，即与第一个分量成直角。

如果原始数据的维数较多，则这一过程还将继续一些额外的步骤：这一过程一直持续到捕捉到数据中的所有差异为止，这将产生与原始数据的维数一样多的分量。因此，PCA 有三个特性：

• 所有成分都不相关。
• 第一个分量变化最大，然后是第二个分量，依此类推。
• 成分的总方差等于原始特征的方差。

PCA 还有一些非常适合离群点检测的特性。如图所示，离群值在各成分中被很好地分离开来，因此可以通过简单的测试来识别离群值。

我们还可以看到 PCA 变换的另一个有趣结果：符合一般模式的点往往落在早期成分中，但在这些成分中会出现极端值（如 A 点），而不符合数据一般模式的点往往不会落在主要成分中，而会在后期成分中出现极端值（如 B 点）。

使用 PCA 识别离群值有两种常见方法：

• 我们可以使用 PCA 对数据进行转换，然后在每个分量上使用一组测试（方便的是，这些测试一般都非常简单），对每一行进行评分。这对编码来说非常简单。
• 我们可以看看重建误差。从图中我们可以看到，仅使用第一个分量就能很好地描述大部分数据。第二个分量是完全描述所有数据所必需的，但只需将数据投影到第一个分量上，我们就能合理地描述大部分数据的位置。但 B 点是个例外；它在第一个分量上的位置并不能很好地描述其全部位置，如果只用一个分量来描述这一点，会产生很大的重建误差，而其他点则不会。一般来说，要很好地描述一个点的位置所需的分量越多（或在分量数量固定的情况下误差越大），该点的离群值就越大。

另一种方法是每次删除一行，然后找出对 PCA 计算结果影响最大的行。虽然这种方法效果不错，但通常速度较慢，而且不常用。

重构误差是离群点检测中常见的一般方法的一个例子。我们以这样或那样的方式建立数据模型，以捕捉数据中的主要模式（例如，使用频繁项目集、聚类、创建预测模型以从其他列预测每一列等）。这些模型往往能很好地拟合大部分数据，但也往往不能很好地覆盖异常值。这些异常值就是与模型不完全匹配的记录。这些记录可能是频繁项目集不能很好代表的记录，也可能是不适合任何聚类的记录，或者是无法从记录中的其他值很好地预测其值的记录。在这种情况下，离群值就是 PCA 主要成分（第一成分）不能很好代表的记录。

用于离群值检测的 PCA 假设

PCA 假定特征之间存在相关性。由于数据之间存在相关性，因此可以对上述数据进行转换，使第一个分量捕捉到的方差远远大于第二个分量捕捉到的方差。在特征之间没有关联的情况下，PCA 对离群点检测的价值不大，但考虑到大多数数据集都有显著的相关性，PCA 通常是适用的。有鉴于此，我们通常可以找到合理数量的成分来捕捉数据集中的大部分方差。

与其他一些常见的离群点检测技术（包括椭圆包络法、高斯混合模型和马哈拉诺比斯距离计算）一样，PCA 的工作原理是创建一个代表数据一般形状的协方差矩阵，然后用它来转换空间。事实上，椭圆包络法、Mahalanobis 距离和 PCA 之间有很强的对应关系。

协方差矩阵是一个 d x d 矩阵（其中 d 是数据中的特征数或维数），它存储了每对特征之间的协方差，每个特征的方差存储在主对角线上（即每个特征对自身的协方差）。协方差矩阵与数据中心一起，是对数据的简明描述--也就是说，每个特征的方差和特征之间的协方差往往是对数据的很好描述。

具有三个特征的数据集的协方差矩阵可能如下所示：

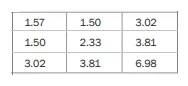
主对角线上显示了三个特征的方差：1.57、2.33 和 6.98。我们还可以得到每个特征之间的协方差。例如，第 1 和第 2 个特征之间的协方差为 1.50。矩阵在主对角线上是对称的，因为第 1 和第 2 个特征之间的协方差与第 2 和第 1 个特征之间的协方差相同，以此类推。

用于离群点检测的 PCA 的局限性

PCA 的一个局限是，它对异常值很敏感。它的基础是最小化点到成分的平方距离，因此会受到异常值的严重影响（偏远点的平方距离可能非常大）。为了解决这个问题，通常会使用稳健 PCA，即在进行转换之前，去除每个维度的极端值。下面的示例就包含了这一点。

PCA 的另一个局限性（以及 Mahalanobis 距离和类似方法）是，如果相关性只存在于数据的某些区域，那么 PCA 就会失效，而如果数据是聚类的，则经常会出现这种情况。在数据聚类较好的情况下，可能有必要先对数据进行聚类（或分割），然后对每个数据子集执行 PCA。

PyOD 中基于 PCA 的异常值测试

现在，我们已经了解了 PCA 的工作原理，以及如何将其应用于离群值检测的高层次方法，我们可以来看看 PyOD 提供的检测器。

PyOD 实际上提供了三种基于 PCA 的类别：PyODKernelPCA、PCA 和 KPCA。我们将逐一了解。

PyODKernelPCA

PyOD 提供了一个名为 PyODKernelPCA 的类，它只是 scikit-learn 的 KernelPCA 类的一个封装。在不同情况下，二者都可能更方便。这个类本身并不是离群点检测器，它只提供 PCA 变换（和逆变换），类似于前面例子中使用的 scikit-learn 的 PCA 类。

但 KernelPCA 类与 PCA 类不同，KernelPCA 允许对数据进行非线性变换，可以更好地模拟一些更复杂的关系。在这种情况下，核的作用与 SVM 模型类似：它们（以一种非常有效的方式）转换空间，使异常值更容易被分离出来。

PCA 检测器

PyOD 提供了两种基于 PCA 的离群点检测器：PCA 类和 KPCA。后者与 PyODKernelPCA 一样，允许内核处理更复杂的数据。PyOD 建议在数据包含线性关系时使用 PCA 类，否则使用 KPCA。

这两类方法都使用数据的重构误差，使用点到超平面的欧氏距离，超平面是用前 k 个分量创建的。其原理同样是，前 k 个分量能很好地捕捉数据的主要模式，而没有被这些分量很好地建模的点都是离群点。

如果将 k 设为 1，我们将只使用一个分量（第一个分量），并测量每个点从其实际位置到该分量上的位置的距离。B 点的距离较大，因此会被标记为离群点。

如同 PCA 一般，在拟合数据之前，最好先移除任何明显的异常值。在下面的例子中，我们使用了 PyOD 提供的另一种检测器，名为 ECOD（经验累积分布函数）。ECOD 是一个你可能不太熟悉的检测器，但却是一个相当强大的工具。事实上，PyOD 建议在为一个项目寻找检测器时，从 Isolation Forest 和 ECOD 开始。

一般来说，在进行离群点检测时（不仅仅是使用 PCA 时），首先清理数据是非常有用的，在离群点检测中，清理数据通常是指去除任何强离群点。这样，离群值检测器就能适应更典型的数据，从而更好地捕捉数据中的强模式（这样就能更好地识别这些强模式的例外情况）。在这种情况下，清理数据可以让 PCA 计算在更典型的数据上进行，从而更好地捕捉数据的主要分布。

在执行之前，有必要安装 PyOD：

pip install pyod

这里的代码使用的是 OpenML 的语音数据集（公共许可证），其中有 400 个数字特征。不过，任何数值数据集都可以使用（任何分类列都需要编码）。此外，一般情况下，任何数字特征都需要进行缩放，使其相互之间的比例相同。

import pandas as pd
from pyod.models.pca import PCA
from pyod.models.ecod import ECOD
from sklearn.datasets import fetch_openml
#A Collects the data
data = fetch_openml("speech", version=1, parser='auto') 
df = pd.DataFrame(data.data, columns=data.feature_names)
scores_df = df.copy()
# Creates an ECOD detector to clean the data
clf = ECOD(contamination=0.01) 
clf.fit(df)
scores_df['ECOD Scores'] = clf.predict(df)
# Creates a clean version of the data, removing the top 
# outliers found by ECOD
clean_df = df[scores_df['ECOD Scores'] == 0] 
# Fits a PCA detector to the clean data
clf = PCA(contamination=0.02) 
clf.fit(clean_df)
# Predicts on the full data
pred = clf.predict(df) 

运行后，pred 变量将包含数据中每条记录的离群值。

KPCA 检测器

KPCA 检测器的工作原理与 PCA 检测器大致相同，不同之处在于对数据应用了指定的内核。这可以使数据发生很大的变化。这两种检测器可以标记出非常不同的记录，由于两者的可解释性都很低，因此很难确定其原因。与离群点检测的常见情况一样，要确定哪种检测器和参数最适合你的数据，可能需要进行一些实验。由于这两种检测器都很强，因此同时使用这两种检测器可能也很有用。

要使用线性内核创建 KPCA 检测器，我们可以使用以下代码：

det = KPCA(kernel='linear')'linear')

KPCA 还支持多项式、径向基函数、正余弦和余弦核。

结论

在本文中，我们介绍了 PCA 背后的理念以及它如何帮助离群点检测，尤其是对 PCA 变换数据的标准离群点检测测试和重构误差进行了研究。我们还研究了 PyOD 提供的两种基于 PCA 的离群值检测器（均使用重构误差），即 PCA 和 KPCA，并提供了一个使用前者的示例。