训练一个有监督的机器学习模型，无论是传统模型还是深度学习模型，都包含几个步骤。首先是将数据输入模型，生成预测。其次是将这些预测与实际值（也称为真实值）进行比较。最后是基于某些目标函数的最小化来优化模型。

在这个迭代过程中，模型会变得越来越好，有时甚至变得非常好。

但你会输入什么数据呢？

有时，你的输入样本会包含许多列，也称为特征。众所周知（尤其是在传统模型中），在你的机器学习模型中使用每一列都会带来麻烦，即所谓的“维度诅咒”。在这种情况下，你必须选择性地处理你正在使用的特征。在本文中，我们将介绍主成分分析（PCA），它就是这样一种方法。本文为你的机器学习模型使用PCA进行特征提取提供了一个温和但全面的介绍。

什么是主成分分析？

在我们深入探讨PCA的具体内容之前，我认为我们首先应该看看为什么它对于机器学习项目来说非常有用。为此，我们将首先看看机器学习项目和维度诅咒，这在使用较旧的机器学习算法（支持向量机、逻辑回归等）时尤其明显。

然后，我们将讨论可以对此采取什么措施——降维——并解释特征选择和特征提取之间的区别。最后，我们将讨论PCA——并提供一个高级别的介绍。

机器学习和维度诅咒

如果你正在训练一个有监督的机器学习模型，那么从高层次上讲，你遵循的是一个三步迭代过程：

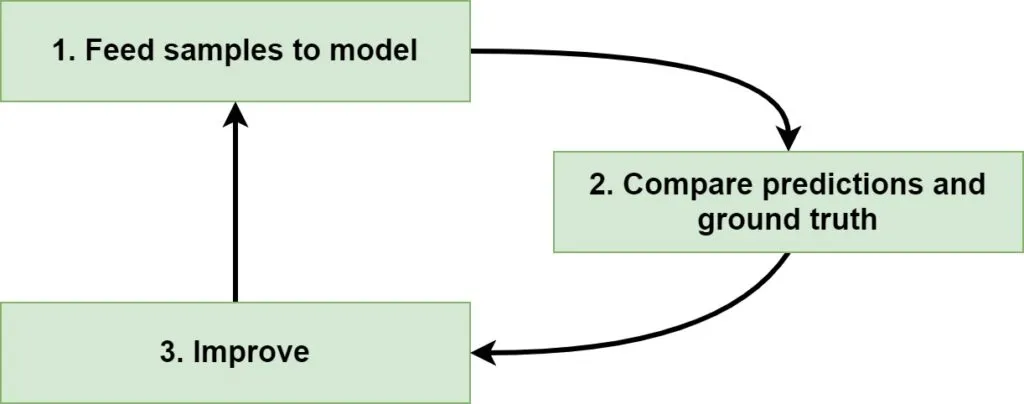
由于监督学习意味着你有一个可用的数据集，因此训练模型的第一步是将样本输入模型。对于每个样本，都会生成一个预测。请注意，在第一次迭代时，模型刚刚初始化。因此，这些预测可能根本没有意义。

这一点在第二步中变得尤其明显，即比较预测值和真实值（=实际目标）。这种比较会产生一个误差或损失值，表明模型的性能有多差。

第三步则非常简单：改进模型。根据不同的机器学习算法，优化以不同的方式进行。在神经网络的情况下，梯度是通过反向传播计算的，随后使用优化器（未来博客的主题）来改变模型内部。权重也可以通过最小化一个函数来改变；这完全取决于算法。

然后，你重新开始。很可能因为已经优化了模型，现在的预测会稍微好一些。你只需要不断迭代，直到对结果满意为止，然后停止训练过程。

模型的欠拟合和过拟合

当你执行这个迭代过程时，你实际上是在从一个欠拟合的模型转向一个表现出良好拟合的模型。让我们在这里简要地看看它们。

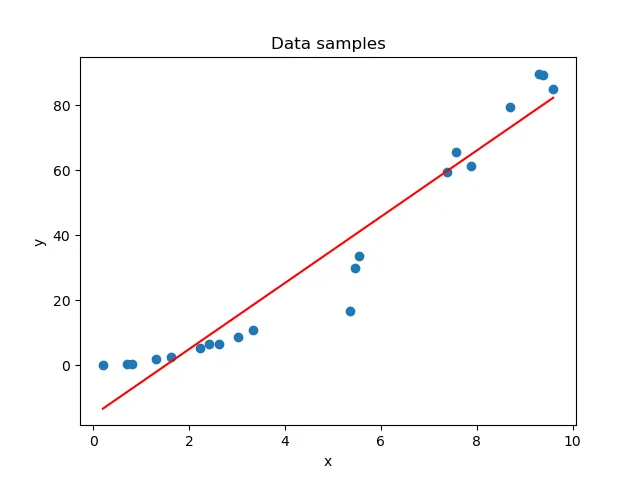
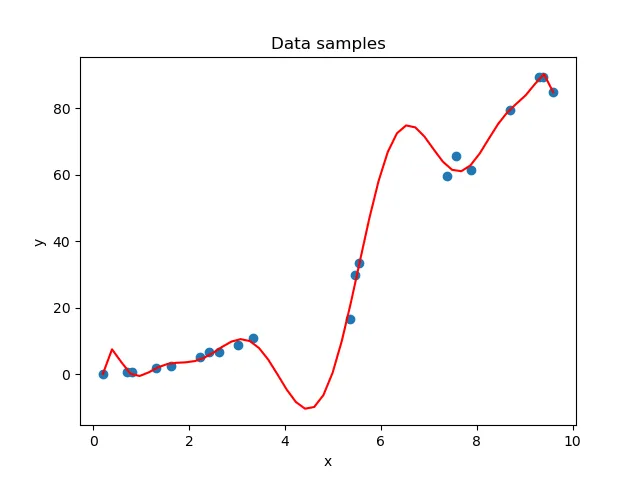
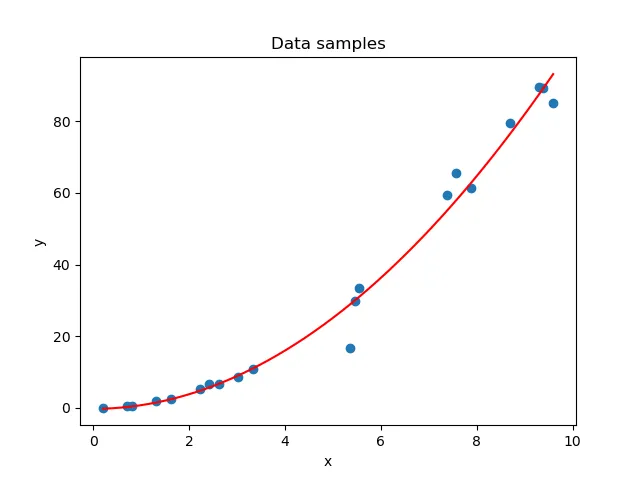
在训练过程的最初阶段，你的模型可能无法捕捉到数据集中的模式。这在下面的上图中可见。解决方案很简单：继续训练，直到你找到适合数据集的拟合（即下图）。然而，你不能永远训练下去。如果你这样做，模型将过于关注训练数据集中隐藏的模式——这些模式可能根本不存在于其他真实世界数据中；这些模式是与你正在训练的样本真正特有的。

结果：一个针对你的特定数据集量身定制的模型，如第二图所示。

换句话说，训练机器学习模型需要在欠拟合模型和过拟合模型之间找到一个良好的平衡。幸运的是，有许多技术可以帮助你实现这一点，但这也是当今监督式机器学习中最常见的问题之一。

拥有高维特征向量

过拟合、欠拟合以及训练机器学习模型——它们与主成分分析（PCA）有何关系？

这是个合理的问题。我想说明的是，为什么一个列数众多的大型数据集会显著增加模型过拟合的风险。

假设你有一个如下的特征向量：

f{x} = [1.23, -3.00, 45.2, 9.3, 0.1, 12.3, 8.999, 1.02, -2.45, -0.26, 1.24]

这个特征向量是11维的。

现在再假设你有200个样本。

机器学习模型能否在这11个维度上都实现良好的泛化？换句话说，我们是否有足够的样本来覆盖向量中所有特征（即11维空间中的所有轴）的大部分域？还是它看起来像是满是（巨大）空洞的瑞士奶酪？

维度诅咒

引用维基百科的话：

在机器学习问题中，当需要从高维特征空间中的有限数量数据样本中学习“自然状态”，且每个特征都有一系列可能的值时，通常需要大量的训练数据来确保每种值组合都有多个样本。

这和我们刚才说的意思是一样的，只是换了一种表述。

“确保每种值组合都有多个样本”这一点意味着，当这一点做得很好时，你很可能能够训练出一个（1）表现良好且（2）能在多种环境下良好泛化的模型。然而，只有200个样本，可以肯定的是，你无法满足这一要求。其结果是：你的模型将会对当前的数据过拟合，而如果将其应用于真实世界的数据，它将变得毫无价值。

由于维度的增加意味着对数据的需求也在不断增加，因此摆脱这种诅咒的唯一方法就是减少数据集中的维度数量。这被称为降维，我们现在来看看两种降维方法——特征选择和特征提取。

降维：特征选择与特征提取

我们已经知道，如果想要降低过拟合的风险，就必须降低数据的维度。虽然在理论上这很容易做到（我们只需要简单地去掉一些维度，谁在乎呢？），但在实践中这却稍微有些困难（应该去掉哪个维度……因为，我怎么知道哪个维度对模型的贡献最大呢？）。

如果每个维度对模型的预测能力都有相同的贡献呢？那又该怎么办？

在降维领域，你可以使用两种主要方法：特征选择和特征提取。

• 特征选择涉及“选择用于模型构建的相关特征（变量、预测器）的子集”（维基百科，2004年）。换句话说，特征选择方法试图衡量每个特征的贡献，以便你可以保留贡献最大的那些特征。必须明确的是，你的模型将使用原始变量进行训练，但只使用其中的一部分。
• 如果你已经认为数据集中的大部分方差可以由少数几个变量来解释，那么特征选择可能是一个好主意。如果其他变量确实不重要，那么你可以轻松地丢弃它们而不会丢失太多信息。
• 另一方面，特征提取“从一组初始测量数据开始，构建旨在提供信息且不冗余的派生值（特征）”（维基百科，2003年）。换句话说，将构建一个派生数据集，可用于训练你的机器学习模型。与原始数据集相比，它的维度更低。它将尽可能具有信息性（即，将尽可能多的原始数据集信息推入新变量中），同时避免冗余（即，我们希望避免新数据集中的一个变量中存在的信息也出现在另一个变量中）。换句话说，我们得到了一个低维数据集，它解释了数据集中的大部分方差，同时保持了相对简单性。
• 特别是在每个维度贡献相等的情况下，特征提取可能比特征选择更受欢迎。如果你不知道每个变量对模型预测能力的贡献，也是如此。

介绍主成分分析（PCA）

既然我们已经了解了这两种方法，现在是时候进入正题了。我们现在将介绍一种用于降维的特征提取技术 PCA。

主成分分析的定义如下：

主成分分析（PCA）是计算主成分并使用它们对数据执行基变换的过程，有时仅使用前几个主成分并忽略其余部分。
维基百科（2002年）

嗯，这是一个相当技术性的描述，不是吗？那么“主成分”是什么呢？

在实p空间中点的集合的主成分是p个方向向量的序列，其中第i个向量是最佳拟合数据的线的方向，同时与前i-1个向量正交。
维基百科（2002年）

PCA的目标：找到一组向量（主成分），这些向量最好地描述了数据在其多个维度上的分布和传播方向，从而允许你随后选择前n个最能描述的向量来降低特征空间的维度。

PCA的步骤：

1. 如果你有一个数据集，它的分布可以用正交归一化向量来表示——数据集的主要方向。在这里，“正交归一化”意味着这些向量彼此正交（即它们之间的角度为90°）并且大小为1。
2. 通过按照重要性对这些向量进行排序（通过查看它们对数据整体分布的相对贡献），我们可以找到解释数据大部分方差的维度。
3. 然后，我们可以将维度数量减少到最重要的那些维度。
4. 最后，我们可以将数据集投影到这些新的维度上，这些新的维度被称为主成分，从而在不丢失数据集中太多信息的情况下实现降维。

如何操作：

尽管我们将在本文后面解释如何操作，但现在我们将在高层次上直观地介绍执行PCA的过程。这可以让你在深入了解它是如何发生之前先理解发生了什么。

另一个重要的一点是，对于步骤（1），将你的数据集分解为向量可以通过两种不同的方式完成——（a）协方差矩阵的特征向量分解，或（b）奇异值分解。在本文的后面部分，我们将逐步介绍这两种方法。

用向量表示数据集的分布

假设我们基于两个重叠的blob生成一个数据集，我们认为它们是同一个数据集的一部分：

from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
# Configuration options
num_samples_total = 1000
cluster_centers = [(1,1), (1.25,1.5)]
num_classes = len(cluster_centers)
# Generate data
X, y = make_blobs(n_samples = num_samples_total, centers = cluster_centers, n_features = num_classes, center_box=(0, 1), cluster_std = 0.15)
e)
# Make plot
plt.scatter(X[:, 0], X[:, 1])
axes = plt.gca()
axes.set_xlim([0, 2])
axes.set_ylim([0, 2])
plt.show()

其内容如下：

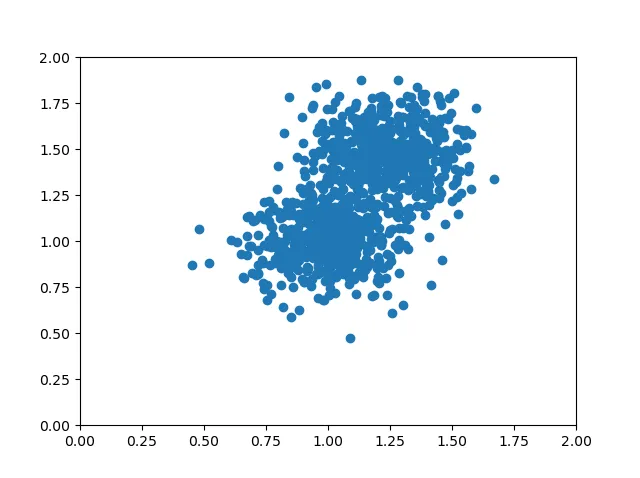
如果你仔细观察这个数据集，你会发现它主要向两个方向扩散。这两个方向一个是从右上角到左下角，另一个是从右下方中间到左上方中间。这些方向与彼此正交的坐标轴方向不同：x轴和y轴之间的夹角是90度。

没有其他任何一组方向能比我们上面提到的这组方向更好地解释数据的方差。

经过标准化处理后，我们可以将这两个方向可视化为一对向量。这些向量被称为数据的主方向（StackExchange，无日期）。主方向的数量与维度的数量相同；在我们的例子中，有两个主方向。

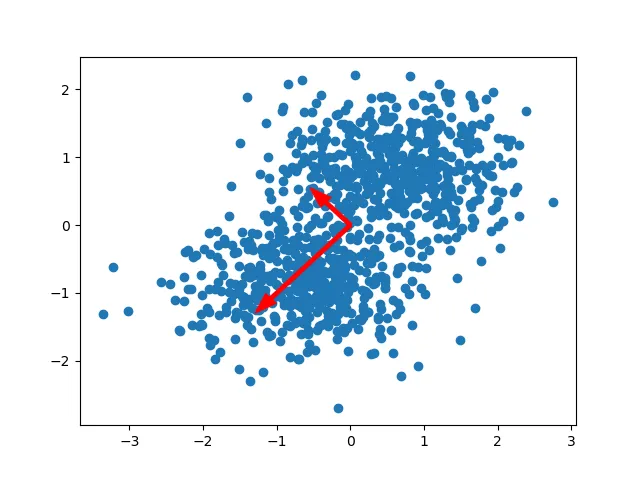
我们称这些向量为特征向量。它们的长度由特征值表示。它们在主成分分析（PCA）中发挥着重要作用。

换句话说，它们使我们能够捕捉到数据集中（1）扩散的方向和（2）扩散的幅度。

请注意，这些向量是彼此正交的。同时回想一下，我们的坐标轴也是彼此正交的。你现在也许可以想象，有可能对你的数据集进行一种变换，使得坐标轴的方向与特征向量的方向相同。换句话说，我们改变了数据的“视角”，使坐标轴和向量具有相同的方向。

这是PCA的核心：将数据投影到我们的主方向上，这些方向随后被称为主成分。

这样做的好处是，虽然特征向量告诉了我们投影的方向，但相应的特征值则告诉了我们特定主方向在解释数据集方差方面的重要性。这使我们能够轻松地舍弃那些贡献不足的方向。因此，在将数据集投影到主成分上之前，我们必须先对向量进行排序并减少维数。

按重要性对向量进行排序

一旦我们知道了能够解释数据集扩散的特征向量和特征值，就必须按降序排列它们的重要性。这样我们就可以进行降维，因为我们只保留对数据集扩散贡献最大的主方向。

排序很简单：我们按降序对特征值列表进行排序，并确保我们的特征向量列表以相同的方式排序。换句话说，特征向量和特征值的配对是根据特征值按降序联合排序的。由于最大的特征值表示对数据集扩散的最大解释，因此它们必须位于列表的顶部。

在上面的例子中，我们可以看到向下定向的特征向量的特征值超过了向上定向的向量的特征值。如果我们在数据集中画一条与这个向量重叠的线，我们也可以看到这条线整体上的方差（其中方差定义为每个点到该线均值的平方距离）是最大的。我们简直无法画出方差更大的线。

事实上，在我们这个例子中，特征向量对扩散的总（相对）贡献如下：

[0.76318124 0.23681876]

降低维度数量

正如我们上面看到的，第一特征对解释了数据集中76.3%的扩散，而第二特征对只解释了23.7%。两者共同解释了100%的扩散，这是合理的。

现在使用PCA进行降维，允许我们只取贡献最大的向量（如果你的原始特征空间是10维的，那么很可能你可以找到一组更小的向量来解释大部分的方差），并只使用它们进行后续操作。

如果我们的目标是将维度降低到一维，那么我们现在就会选择贡献率为0.763的特征向量进行数据投影。请注意，这意味着我们将失去关于扩散的0.237的信息，但换来的是更低的维度数量。

显然，这个只有两个维度的例子在理性上是没有意义的，因为两个维度可以很容易地被机器学习算法处理，但如果你有很多维度需要处理，这将是非常有用的。

投影数据集

一旦我们选择了将用于降维的特征向量数量（即我们的目标维度数量），我们就可以将数据投影到主成分上——在我们的例子中是主成分。

这意味着我们将改变坐标轴，使它们现在与特征向量相等。

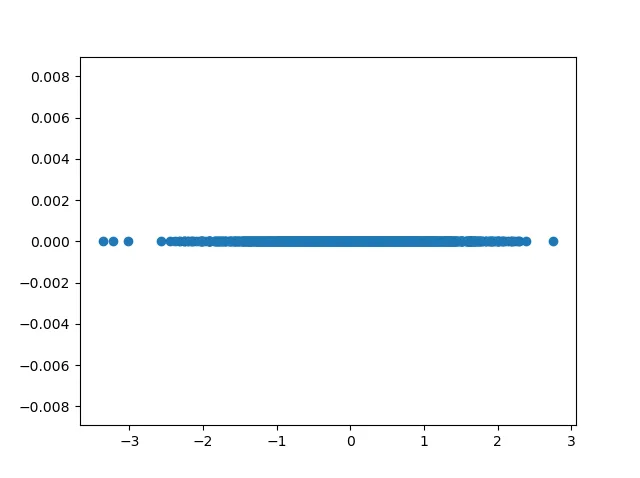
在下面的例子中，我们可以将数据投影到一个特征向量上。我们可以看到，投影后只有x轴有值，因此我们的特征空间已经降低到了一维。

因此，我们已经使用PCA进行了降维。

生成特征对的方法：特征向量分解或奇异值分解

之前，我们概述了执行主成分分析（PCA）的一般步骤。回顾一下，它们是：

1. 将数据集分解为一组特征对。
2. 按重要性降序对特征对进行排序。
3. 选择n个最重要的特征对，其中n是所需维度数。
4. 将数据投影到n个特征对上，使它们的方向与我们的坐标轴方向一致。

在第（1）步中，我们简单地提到可以通过特征对来表示数据的扩散。为了简化，我们故意没有解释这是如何实现的。

事实上，今天有两种方法被用于这个目的：特征向量分解（通常称为“EIG”）和奇异值分解（“SVD”）。尽管它们使用不同的方法，但可以用来获得相同的最终结果：用特征对（即数据的主方向）来表示数据集的扩散，随后可以通过将数据集投影到最重要的主成分上来减少维度数。

虽然在数学上，因此也在形式上，你可以使用这两种方法获得相同的结果，但在实践中，PCA-SVD在数值上更稳定（StackExchange，无日期）。出于这个原因，你会发现大多数库和框架都倾向于使用PCA-SVD实现，而不是PCA-EIG。尽管如此，你仍然可以通过这两种方法获得相同的结果！

PCA-EIG：逐步使用Python进行特征向量分解

执行PCA的方法之一是通过特征向量分解（EIG）。更具体地说，我们可以使用N维数据集的协方差矩阵，并将其分解为N个特征对。我们可以按照以下步骤进行：

1. 标准化数据集：基于EIG的PCA只有在数据集居中且均值为零（即μ=0.0）时才有效。我们将为此使用标准化，这还将数据缩放到标准差为一（σ=1.0）。
2. 计算变量的协方差矩阵：协方差矩阵表示每个单独变量的方差，以及它们“共变”的程度——换句话说，就是某些变量在多大程度上一起变化。
3. 将协方差矩阵分解为特征对：在数学上，我们可以重写协方差矩阵，以获得一组特征向量和特征值，或特征对。
4. 按重要性降序对特征对进行排序，以找到数据集中对扩散贡献最大的主方向。
5. 选择主方向的方差贡献并选择n个主成分：如果我们知道每个主方向对扩散的相对贡献，就可以通过仅选择n个贡献最大的主成分来进行降维。
6. 构建投影矩阵，以将原始数据集投影到主成分上。

我们可以看到，步骤（1）、（4）、（5）和（6）是通用的——我们之前也看到过它们。步骤（2）和（3）是PCA-EIG特有的，代表了基于特征向量分解的PCA的核心。我们现在将更详细地介绍每个步骤，包括使用Python的逐步示例。请注意，本节中的示例故意使用了原生/基础Python。

使用多维鸢尾花数据集

如果我们想展示PCA是如何工作的，我们必须使用一个维度数大于2的数据集。幸运的是，Scikit-learn提供了鸢尾花数据集，该数据集可用于根据四个特征（因此也是维度）对三组鸢尾花进行分类：花瓣长度、花瓣宽度、萼片长度和萼片宽度。

这段代码每次可用于可视化两个维度：

from sklearn import datasets
import matplotlib.pyplot as plt
import numpy as np
# Configuration options
dimension_one = 1
dimension_two = 3
# Load Iris dataset
iris = datasets.load_iris()
X = iris.data
y = iris.target
# Shape
print(X.shape)
print(y.shape)
# Dimension definitions
dimensions = {
  0: 'Sepal Length',
  1: 'Sepal Width',
  2: 'Petal Length',
  3: 'Petal Width'
}
# Color definitions
colors = {
  0: '#b40426',
  1: '#3b4cc0',
  2: '#f2da0a',
}
# Legend definition
legend = ['Iris Setosa', 'Iris Versicolour', 'Iris Virginica']
# Make plot
colors = list(map(lambda x: colors[x], y))
plt.scatter(X[:, dimension_one], X[:, dimension_two], c=colors)
plt.title(f'Visualizing dimensions {dimension_one} and {dimension_two}')
plt.xlabel(dimensions[dimension_one])
plt.ylabel(dimensions[dimension_two])
plt.show()

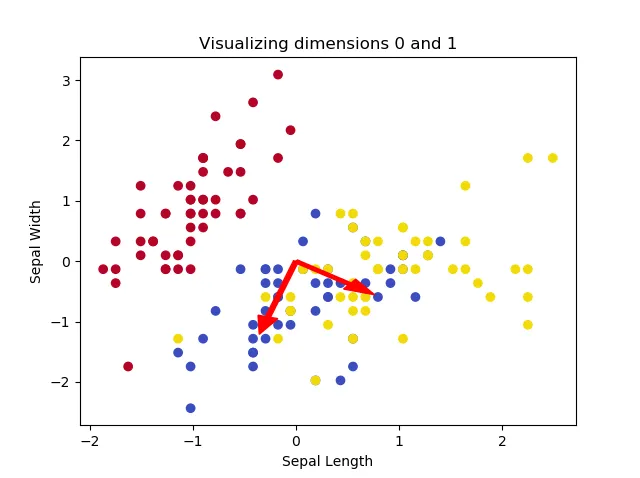
如果我们调整尺寸，就会得到以下图表：

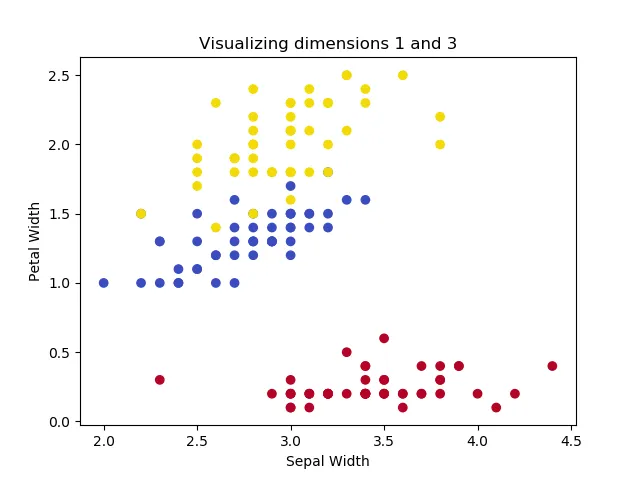
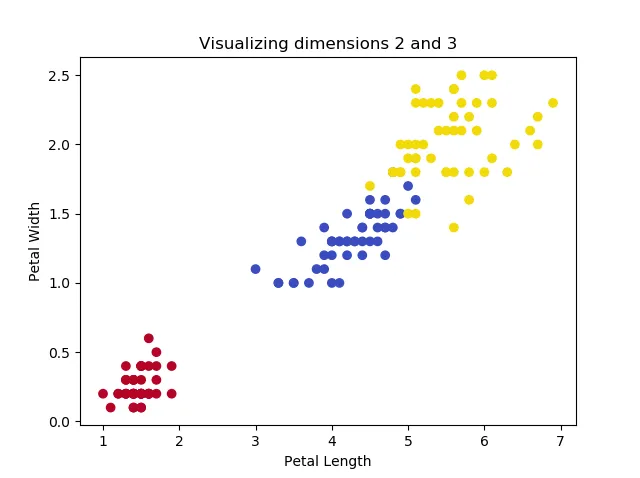
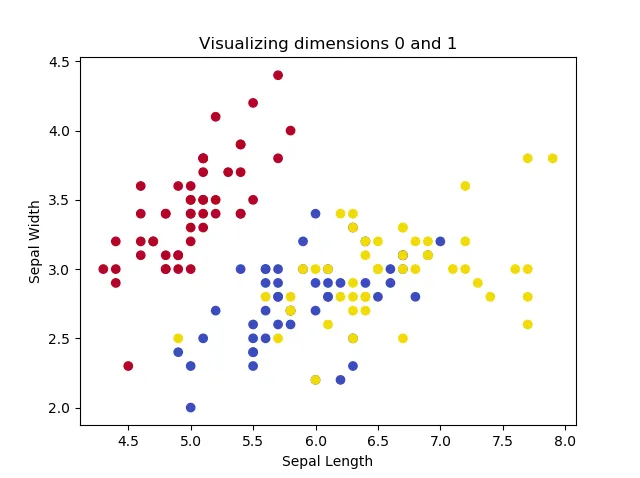
这些图像表明，其中两种鸢尾花无法被线性分离，但是这个群体可以与另一种鸢尾花分离开来。打印形状会得到以下结果：

(150, 4)
(150,)

……这表明我们只有150个样本，但我们的特征空间是四维的。显然，这是一个特征提取可能有益于训练我们机器学习模型的场景。

执行标准化

加Python代码进行标准化，通过对每个维度执行x = (x - μ) / σ，使我们的数据均值μ为0.0，标准差σ为1.0。

# Perform standardization
for dim in range(0, X.shape[1]):
  print(f'Old mean/std for dim={dim}: {np.average(X[:, dim])}/{np.std(X[:, dim])}')
  X[:, dim] = (X[:, dim] - np.average(X[:, dim])) / np.std(X[:, dim])
  print(f'New mean/std for dim={dim}: {np.abs(np.round(np.average(X[:, dim])))}/{np.std(X[:, dim])}')
# Make plot
colors = list(map(lambda x: colors[x], y))
plt.scatter(X[:, dimension_one], X[:, dimension_two], c=colors)
plt.title(f'Visualizing dimensions {dimension_one} and {dimension_two}')
plt.xlabel(dimensions[dimension_one])
plt.ylabel(dimensions[dimension_two])
plt.show()

并且确实：

Old mean/std for dim=0: 5.843333333333334/0.8253012917851409
New mean/std for dim=0: 0.0/1.0
Old mean/std for dim=1: 3.0573333333333337/0.4344109677354946
New mean/std for dim=1: 0.0/0.9999999999999999
Old mean/std for dim=2: 3.7580000000000005/1.759404065775303
New mean/std for dim=2: 0.0/1.0
Old mean/std for dim=3: 1.1993333333333336/0.7596926279021594
New mean/std for dim=3: 0.0/1.0

计算变量的协方差矩阵

如果你不喜欢数学，我能理解你现在可能还不明白这是什么。因此，在我们继续之前，让我们基于Lambers（无日期）的内容，简要地看一下与协方差矩阵相关的几个方面。

变量：如X。它是数据集一个维度的数学表示。例如，如果X代表{花瓣宽度}，那么像1.19、1.20、1.21、1.18、1.16、……这样的数字，代表一朵花的花瓣宽度，都可以用变量X来描述。

变量均值：变量的平均值。计算方法是所有可用值的总和除以值的数量。由于花瓣宽度在上述可视化中代表第三个维度，均值约为1.1993，我们可以看出上面的数字是如何符合这个均值的。

方差：描述数据在变量周围的“分散”程度。计算方法是每个数字与均值的差的平方和，即每个数字的(x-μ)²的和。

协方差：描述两个变量的联合变异性（或联合分散性）。对于来自两个变量的每对数字，协方差计算为：

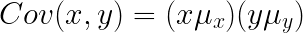
对于n个变量的协方差矩阵：一个矩阵，表示来自某些变量集（维度）V = [X, Y, Z, ……]中每对变量的协方差。

两个维度X和Y的协方差矩阵如下所示：

幸运的是，协方差矩阵具有一些特性，使得它对主成分分析（PCA）非常有趣（Lambers，无日期）：

• [Cov(X, X) = Var(X) （X与自身的协方差等于X的方差）
• Cov(X, Y) = Cov(Y, X) （X与Y的协方差等于Y与X的协方差）

因此，我们的协方差矩阵是一个对称的方阵，即n x n矩阵，因此也可以表示如下：

我们可以通过生成一个(n x n)矩阵，然后迭代其行和列来填充它，将值设置为两个变量中每个相应数字的平均协方差，从而计算出协方差矩阵。

# Compute covariance matrix
cov_matrix = np.empty((X.shape[1], X.shape[1])) # 4 x 4 matrix= np.empty((X.shape[1], X.shape[1])) # 4 x 4 matrix
for row in range(0, X.shape[1]):
  for col in range(0, X.shape[1]):
    cov_matrix[row][col] = np.round(np.average([(X[i, row] - np.average(X[:, row]))*(X[i, col]\
        - np.average(X[:, col])) for i in range(0, X.shape[0])]), 2)

如果我们将自行计算的协方差矩阵与使用NumPy的np.cov生成的协方差矩阵进行比较，可以看到它们的相似之处：

# Compare the matrices
print('Self-computed:')
print(cov_matrix)
print('NumPy-computed:')
print(np.round(np.cov(X.T), 2))
> Self-computed:
> [[ 1. -0.12  0.87  0.82]
>  [-0.12  1. -0.43 -0.37]
>  [ 0.87 -0.43  1. 0.96]
>  [ 0.82 -0.37  0.96  1. ]]
> NumPy-computed:
> [[ 1.01 -0.12  0.88  0.82]
>  [-0.12  1.01 -0.43 -0.37]
>  [ 0.88 -0.43  1.01  0.97]
>  [ 0.82 -0.37  0.97  1.01]]

分解协方差矩阵为特征向量和特征值

在上面，我们已经在协方差矩阵中表达了数据集在各个维度上的分布。回顾一下，PCA的工作原理是用向量（称为特征向量）来表示这种分布，这些向量与它们对应的特征值一起，告诉我们分布的方向和大小。

EIG-PCA的优点在于，我们可以将协方差矩阵分解为特征向量和特征值。

我们可以按照以下步骤进行：

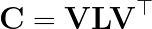
在这里，V是一个特征向量矩阵，其中每一列都是一个特征向量，L是一个对角矩阵，包含特征值，而V^top是V的转置。

我们可以使用NumPy的numpy.linalg.eig来计算这个方阵的特征向量：

# Compute the eigenpairs
eig_vals, eig_vect = np.linalg.eig(cov_matrix)
print(eig_vect)
print(eig_vals)

这会产生以下结果：

[[ 0.52103086 -0.37921152 -0.71988993  0.25784482]
 [-0.27132907 -0.92251432  0.24581197 -0.12216523]
 [ 0.57953987 -0.02547068  0.14583347 -0.80138466]
 [ 0.56483707 -0.06721014  0.63250894  0.52571316]]
[2.91912926 0.91184362 0.144265   0.02476212]

如果我们计算每个主成分维度对方差解释的贡献程度，我们会得到以下结果：

# Compute variance contribution of each vector
contrib_func = np.vectorize(lambda x: x / np.sum(eig_vals))
var_contrib = contrib_func(eig_vals)
print(var_contrib)
print(np.sum(var_contrib))
# > [0.72978232 0.2279609  0.03606625 0.00619053]
# > 1.0

换句话说，第一个主成分维度贡献了73%的方差解释，第二个贡献了23%。因此，如果我们将维度降低到两个，我们就能保留大约73% + 23% = 96%的方差解释。

按重要性递减顺序对特征对进行排序

尽管上面的特征对已经排序，但这是我们必须做的一步——特别是当你以不同的方式执行特征对分解时。

特征对的排序是根据特征值来进行的：特征值必须按降序排序；因此，相应的特征向量也必须以相同的方式进行排序。

# Sort eigenpairs
eigenpairs = [(np.abs(eig_vals[x]), eig_vect[:,x]) for x in range(0, len(eig_vals))]
eig_vals = [eigenpairs[x][0] for x in range(0, len(eigenpairs))]
eig_vect = [eigenpairs[x][1] for x in range(0, len(eigenpairs))]
print(eig_vals)

这产生了排序后的特征对，从特征值我们可以看出这一点：

[2.919129264835876, 0.9118436180017795, 0.14426499504958146, 0.024762122112763244]2.919129264835876, 0.9118436180017795, 0.14426499504958146, 0.024762122112763244]

选择n个主成分

在上面，我们看到仅通过两个维度就可以解释96%的方差。因此，我们可以将特征空间的维度从n=4降低到n=2，而不会丢失太多信息。

构建投影矩阵

我们最后必须做的是生成投影矩阵，并将我们的原始数据投影到（两个）主成分上（Raschka，2015）：

# Build the projection matrix
proj_matrix = np.hstack((eig_vect[0].reshape(4,1), eig_vect[1].reshape(4,1)))
print(proj_matrix)
# Project onto the principal components
X_proj = X.dot(proj_matrix)

完成了，你已经执行了PCA

如果我们现在绘制投影数据，我们会得到以下图表：

# Make plot of projection
plt.scatter(X_proj[:, 0], X_proj[:, 1], c=colors)
plt.title(f'Visualizing the principal components')
plt.xlabel('Principal component 1')
plt.ylabel('Principal component 2')
plt.show()

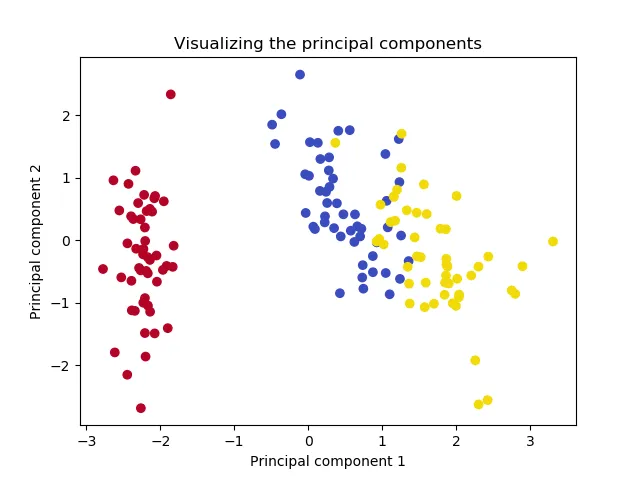
就这样！你刚刚使用特征向量分解执行了主成分分析（PCA），并将维度降低到了两个，而没有丢失数据集中的太多信息。

总结

在本文中，我们了解了如何对数据集的维度执行主成分分析（PCA）以实现降维。一些数据集具有许多特征和少量样本，这意味着许多机器学习算法将受到维度灾难的影响。像PCA这样的特征提取方法尝试基于原始数据集构建一个更低维的特征空间，有助于减轻这种维度灾难。使用PCA，我们可以尝试用更少的维度和最小的信息损失来重新创建我们的特征空间。

在定义了应用PCA的上下文之后，我们从高层次的角度进行了审视。我们看到可以计算特征向量和特征值，并对它们进行排序，以找到数据集中的主要方向。在为这些方向生成投影矩阵后，我们可以将数据集映射到这些方向上，这些方向随后被称为主成分。但是，如何推导这些特征向量在后面才进行了解释，因为有两种方法可以做到这一点：使用特征向量分解（EIG）和更具一般性的奇异值分解（SVD）。

在两个逐步示例中，我们看到了如何应用PCA-EIG（本文）和PCA-SVD（下文）来执行主成分分析。在第一个示例中，我们看到可以为标准化数据集计算协方差矩阵，该矩阵说明了其变量的方差和协方差。然后，这个矩阵可以被分解为特征向量和特征值，它们说明了协方差矩阵所表达的分布的方向和大小。通过对特征对进行排序，我们可以选择对方差贡献最大的主要方向，生成投影矩阵并投影我们的数据。

虽然PCA-EIG对于对称和方阵（以及我们的协方差矩阵）效果很好，但它可能在数值上不稳定。这就是为什么PCA-SVD在当今的机器学习库中非常常见的原因。在另一个逐步示例中，我们将查看如何直接在标准化数据矩阵上使用SVD来推导我们在PCA-EIG中也找到的特征向量。它们可以用于生成投影矩阵，使我们能够得到与执行PCA-EIG时相同的最终结果。