PCA是一种将数据（将数据记录视为高维空间中的点）从一组坐标转换到另一组坐标的方法。如果我们从一个包含100条记录和两个特征的数据集开始（如下方左图所示），那么我们可以将这些数据视为二维空间中的100个点。在实际应用中，我们会有更多记录和更多维度，但原理相同。使用PCA，我们将数据移动到一组新的坐标中，从而有效地为每条记录创建了一组新的描述特征。

因此，如果我们从一个数据集开始，如下方左图所示，我们可以应用PCA转换将数据转换成类似右图所示的形式。在右图中，我们展示了数据被映射到的两个PCA组件。这些组件被简单地命名为0和1。

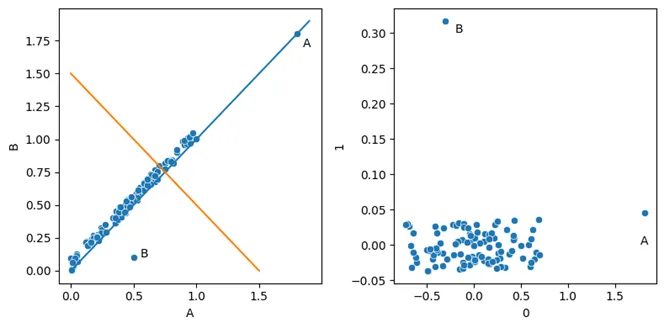
关于PCA组件，有一点需要注意，那就是它们之间是完全不相关的。这是由它们的构建方式决定的；它们基于原始数据中的线、平面或超平面，这些线、平面或超平面都是严格正交的。我们可以在右图中看到，组件0和组件1之间没有任何关系。

这对异常检测有着重要影响；特别是，这意味着异常值往往会在一个或多个组件中被转换成极端值，因此更容易被检测到。这也意味着不需要更复杂的异常检测测试（测试特征之间的不寻常关联），而是可以使用更简单的测试。

单变量和多变量异常检测器

在深入探讨PCA在异常检测中的优势之前，我将简要介绍两种类型的异常检测器。异常检测算法有很多分类方式，但一种有用的方式是区分所谓的单变量测试和多变量测试。

单变量测试

单变量指的是只检查一个特征的测试——即识别该特征中的罕见值或极端值。例如，基于z分数、四分位距（IQR）、十分位距（IDR）、中位数绝对偏差（MAD）的测试，以及直方图测试、核密度估计（KDE）测试等。

PyOD（可能是目前Python中用于表格数据异常检测最完整、最有用的工具）提供的一种基于直方图的测试是HBOS。

正如在异常值检测的 PCA 简介中所述，PyOD 提供的另一种单变量测试是ECOD。

为了描述单变量测试，我们来看一个针对特定现实世界数据集的异常检测示例。下表是从OpenML（可用公共许可证获取）的棒球数据集中提取的一个子集，这里仅显示了三行和五列（完整数据集中还有更多特征）。每一行代表一名球员，包含其各项统计数据，包括他们参赛的赛季数、比赛数等。

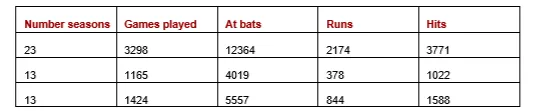
为了找出不寻常的球员，我们可以寻找那些具有不寻常单一数值的记录（例如，参赛赛季异常多、击球次数异常多等等的球员）。这些可以通过单变量测试来发现。

例如，使用 z 分数测试来查找异常记录，我们实际上会对每一列逐一执行 z 分数测试。我们首先检查“季节数”列（评估列中每个值相对于该列的异常程度），然后检查“比赛场次”列，依此类推。

例如，在使用z分数测试检查“参赛赛季数”列时，我们首先需要确定该列的平均值和标准差。（其他测试可能会确定该列的中位数和四分位距、直方图箱形计数等。）

然后，我们将确定“参赛赛季数”列中每个值的绝对z分数：即每个值距离平均值的标准差数量。z分数越大，该值就越不寻常。任何绝对z分数超过4.0或5.0的值都可能被视为异常，尽管这取决于数据的大小和分布。

之后，我们将对其他列重复此过程。完成后，我们将为每一行获得一个分数，表示该行中每个值与其所在列的异常程度。因此，每一行都会有一组分数：该行中每个值一个分数。

接下来，我们需要确定每个记录的总体异常分数。这有多种方法，每种方法都有其细微差别，但两种简单的方法是取每行值的平均z分数或取每行的最大z分数。

多变量测试

多变量测试会同时考虑多个特征。事实上，几乎所有的多变量异常检测器都会同时考虑所有特征。

大多数异常检测器（包括隔离森林、局部异常因子（LOF）、K近邻（KNN）等）都是基于多变量测试的。

这些检测器的优点是，我们可以查找具有异常值组合的记录。例如，一些球员可能有典型的得分数和击球数，但根据他们的击球数，得分可能异常多（或少）。这些可以通过多变量测试来发现。

在上面的散点图（考虑左窗格中的原始数据）中，点A在两个维度上都是极端的，因此可以通过单变量测试来检测。事实上，对特征A的单变量测试可能会标记点A，对特征B的单变量测试也可能如此，因此点A在两个特征上都是异常的，使用单变量测试会给出高分。

然而，点B在两个维度上都是典型的。只有值的组合是不寻常的，为了检测这种异常，我们需要进行多变量测试。

通常，在对表格数据进行异常检测时，我们是在寻找不寻常的行，而不是不寻常的单个值。不寻常的行既包括那些具有不寻常单个值的行，也包括具有不寻常值组合的行。因此，单变量测试和多变量测试通常都很有用。然而，多变量测试可以捕获单变量和多变量异常（在散点图中，像隔离森林、LOF或KNN这样的多变量测试通常可以捕获点A和点B），因此在实际应用中，多变量测试往往使用得更频繁。

尽管如此，在异常检测中，我们经常将分析限制在单变量测试上。单变量测试更快——通常要快得多（这在实时环境或需要评估大量数据的环境中非常重要）。单变量测试也更易于解释。

而且它们不会受到维数灾难的影响。这在计数异常值检测器、共享最近邻居和Python 中的异常值检测中有所介绍，但一般的想法是，当处理过多特征时，多元测试可能会失败。这有许多原因，但其中重要原因是，如果维度足够多，距离计算（许多异常值检测器，包括 LOF 和 KNN 都依赖于此）会变得毫无意义。通常只使用 20 个或更多特征，而使用大约 50 个或更多特征时，异常值分数就会变得不可靠。

与依赖于行之间距离计算的多变量测试相比，单变量测试在更高维度上的扩展性要好得多。

因此，使用单变量测试有一些主要优势。但也有一些主要缺点：它们会错过与异常值组合相关的异常，因此只能检测到相关异常的一部分。

对PCA组件的单变量测试

因此，在大多数情况下，运行多变量测试是有用的（也更常见）。但它们更慢、更难以解释，并且更容易受到维数灾难的影响。

PCA转换的一个有趣效果是，单变量测试变得更加实用。一旦完成PCA转换，特征之间就没有关联了，因此也就没有异常值组合的概念了。

在上面的散点图（右窗格——PCA转换后）中，我们可以看到点A和点B都可以简单地被识别为极端值。点A在组件0上是极端的；点B在组件1上是极端的。

这意味着，我们可以使用简单的统计测试（例如 z 分数、IQR、IDR 或 MAD 测试）或使用简单工具（例如 HBOS 和 ECOD）有效地执行异常值检测。

话虽如此，在使用 PCA 转换数据空间后，仍然可以使用标准多变量测试，例如孤立森林、LOF 或任何其他标准工具。如果这些是我们最常用的工具，那么继续使用它们会很方便，只需先使用 PCA 作为预处理步骤转换数据即可。

与统计方法（例如 z 分数等）相比，它们提供的一项优势是它们会自动为每条记录提供单个异常值分数。 如果我们对每条记录使用 z 分数检验，且数据有 20 个特征，我们将其转换为 10 个成分（可以不使用所有成分，如下所述），则每条记录将有 10 个异常值分数 - 每个分数与它在所使用的 10 个成分中的不寻常程度有关。 然后需要将这些分数组合成一个异常值分数。 如上所述，有简单的方法可以做到这一点（包括对每行每个值取平均值、中位数或最大 z 分数），但这样做会有一些复杂之处（如 Python 中的异常值检测中所述）。 这很容易管理，但让检测器提供单个分数也很方便。

使用 PCA 进行异常值检测的示例

现在，我们将看一个使用 PCA 来帮助更好地识别数据集中的异常值的示例。为了更容易理解异常值检测如何与 PCA 配合使用，我们将在此示例中创建两个非常简单的合成数据集。我们将创建具有 100,000 行和 10 个特征的数据集。然后我们添加一些已知的异常值，有点类似于上面散点图中的点 A 和 B。

为简单起见，我们将数据集限制为 10 个特征，但正如上文和上一篇文章所建议的那样，在高维空间中使用 PCA 可以带来很大的好处，因此（尽管本例中没有涉及）使用具有数百个特征的 PCA 比使用 10 个特征的 PCA 更有优势。不过，这里使用的数据集相当容易使用和理解。

创建第一个数据集 data_corr 是为了使特征之间具有强关联（相关性）。我们更新最后一行以包含一些较大的（但不是特别大）值。最重要的是，这一行偏离了特征之间的正常模式。

我们创建另一个名为 data_extreme 的测试数据集，该数据集与特征之间没有任何关联。修改该数据集的最后一行以包含某些特征的极值。

这使我们能够使用两个易于理解的数据分布以及易于理解的异常值类型进行测试（我们在 data_corr 中有一个异常值，它忽略了特征之间的正常相关性；并且我们在 data_extreme 中有一个异常值，它在某些特征中具有极端值）。

此示例使用了多个 PyOD 检测器，需要首先执行：

pip install pyod

然后，代码开始创建第一个测试数据集：

import numpy as np
import pandas as pd
from sklearn.decomposition import PCA
from pyod.models.ecod import ECOD
from pyod.models.iforest import IForest
from pyod.models.lof import LOF
from pyod.models.hbos import HBOS
from pyod.models.gmm import GMM
from pyod.models.abod import ABOD
import time
np.random.seed(0)
num_rows = 100_000
num_cols = 10
data_corr = pd.DataFrame({0: np.random.random(num_rows)}) 
for i in range(1, num_cols):
  data_corr[i] = data_corr[i-1] + (np.random.random(num_rows) / 10.0)
copy_row = data_corr[0].argmax()
data_corr.loc[num_rows-1, 2] = data_corr.loc[copy_row, 2]
data_corr.loc[num_rows-1, 4] = data_corr.loc[copy_row, 4]
data_corr.loc[num_rows-1, 6] = data_corr.loc[copy_row, 6]
data_corr.loc[num_rows-1, 8] = data_corr.loc[copy_row, 8]
start_time = time.process_time() 
pca = PCA(n_components=num_cols)
pca.fit(data_corr)
data_corr_pca = pd.DataFrame(pca.transform(data_corr), 
 columns=[x for x in range(num_cols)])
print("Time for PCA tranformation:", (time.process_time() - start_time))

现在我们已经有了第一个测试数据集data_corr。在创建这个数据集时，我们将每个特征设置为之前特征的和加上一些随机性，因此所有特征都是高度相关的。最后一行被故意设置为一个异常值。虽然这些值很大，但并没有超出已有数据的范围。然而，已知异常值中的数值并不遵循特征之间的正常模式。

接下来，我们计算这个数据集的PCA（主成分分析）变换。

然后，我们对另一个测试数据集也进行同样的操作：

np.random.seed(0)0)
 
data_extreme = pd.DataFrame()
for i in range(num_cols):
    data_extreme[i] = np.random.random(num_rows)
copy_row = data_extreme[0].argmax()
data_extreme.loc[num_rows-1, 2] = data_extreme[2].max() * 1.5
data_extreme.loc[num_rows-1, 4] = data_extreme[4].max() * 1.5
data_extreme.loc[num_rows-1, 6] = data_extreme[6].max() * 1.5
data_extreme.loc[num_rows-1, 8] = data_extreme[8].max() * 1.5
start_time = time.process_time() 
pca = PCA(n_components=num_cols)
pca.fit(data_corr)
data_extreme_pca = pd.DataFrame(pca.transform(data_corr), 
    columns=[x for x in range(num_cols)])
print("Time for PCA tranformation:", (time.process_time() - start_time))

在这里，每个特征都是独立创建的，因此特征之间没有关联。每个特征仅仅遵循一个均匀分布。最后一行被设置为异常值，在第2、4、6和8个特征（即十个特征中的四个）中具有极端值。

现在我们已经有了两个测试数据集。接下来，我们定义一个函数，该函数在给定数据集和检测器的情况下，将在完整数据集上训练检测器，并在同一数据上进行预测（即在单个数据集中识别异常值），同时记录这两个操作的时间。对于ECOD（经验累积分布）检测器，我们添加了特殊处理来创建一个新实例，以避免保留之前执行过程中的记忆（对于其他检测器则没有必要这样做）。

def evaluate_detector(df, clf, model_type):
    """
    params:
    df: data to be assessed, in a pandas dataframe
    clf: outlier detector
    model_type: string indicating the type of the outlier detector
    """
    global scores_df
 
    if "ECOD" in model_type:
       clf = ECOD()
    start_time = time.process_time()
    clf.fit(df)
    time_for_fit = (time.process_time() - start_time)
    start_time = time.process_time()
    pred = clf.decision_function(df)
    time_for_predict = (time.process_time() - start_time)
 
    scores_df[f'{model_type} Scores'] = pred
    scores_df[f'{model_type} Rank'] =\
    scores_df[f'{model_type} Scores'].rank(ascending=False)
  
    print(f"{model_type:<20} Fit Time: {time_for_fit:.2f}")
    print(f"{model_type:<20} Predict Time: {time_for_predict:.2f}")

接下来定义的函数会对每个数据集执行操作，对每个数据集调用之前的方法。在这里，我们测试四种情况：使用原始数据、使用PCA转换后的数据、使用PCA转换后数据的前3个主成分，以及使用PCA转换后数据的后3个主成分。这将告诉我们这四种情况在时间和准确性方面的比较结果。

def evaluate_dataset_variations(df, df_pca, clf, model_name): 
    evaluate_detector(df, clf, model_name)
    evaluate_detector(df_pca, clf, f'{model_name} (PCA)')
    evaluate_detector(df_pca[[0, 1, 2]], clf, f'{model_name} (PCA - 1st 3)')
    evaluate_detector(df_pca[[7, 8, 9]], clf, f'{model_name} (PCA - last 3)')

如下所述，在这里仅使用最后三个主成分在准确性方面表现良好，但在其他情况下，使用前面的主成分（或中间的主成分）也可能表现良好。此处将其作为一个示例包含在内，但文章的其余部分将仅关注使用最后三个主成分的选项。

为每个数据集定义了最后一个要调用的函数。它为这里测试的每个检测器执行前面的函数。在这个例子中，我们使用了来自PyOD的六个检测器：隔离森林（Isolation Forest）、局部离群因子（LOF）、经验累积分布（ECOD）、基于直方图的离群点检测（HBOS）、高斯混合模型（GMM）和基于角度的离群点检测（ABOD）。

def evaluate_dataset(df, df_pca): 
  clf = IForest()
  evaluate_dataset_variations(df, df_pca, clf, 'IF')
  
  clf = LOF(novelty=True)
  evaluate_dataset_variations(df, df_pca, clf, 'LOF')
  clf = ECOD()
  evaluate_dataset_variations(df, df_pca, clf, 'ECOD')
  clf = HBOS()
  evaluate_dataset_variations(df, df_pca, clf, 'HBOS')
  clf = GMM()
  evaluate_dataset_variations(df, df_pca, clf, 'GMM')
  clf = ABOD()
  evaluate_dataset_variations(df, df_pca, clf, 'ABOD')

最后，我们为两个测试数据集调用evaluate_dataset()方法，并打印出最主要的异常值（已知异常值位于两个测试数据集的最后一行中）：

# Test the first dataset
# scores_df stores the outlier scores given to each record by each detector
scores_df = data_corr.copy()
evaluate_dataset(data_corr, data_corr_pca)
rank_columns = [x for x in scores_df.columns if type(x) == str and 'Rank' in x]
print(scores_df[rank_columns].tail())
# Test the second dataset
scores_df = data_extreme.copy()
evaluate_dataset(data_extreme, data_extreme_pca)
rank_columns = [x for x in scores_df.columns if type(x) == str and 'Rank' in x]
print(scores_df[rank_columns].tail())

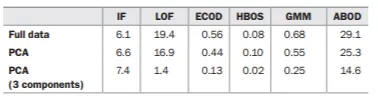
有几个有趣的结果。我们首先查看data_corr数据集的拟合时间，如下表所示（另一个测试集的拟合和预测时间类似，因此未在此处展示）。测试是在Google Colab上进行的，时间以秒为单位显示。我们可以看到，不同的检测器所需时间差异很大。ABOD明显比其他检测器慢，而HBOS则快得多。此处包含的另一个单变量检测器ECOD也非常快。

对PCA转换后的数据进行拟合的时间与原始数据大致相同，考虑到数据大小相同，这是合理的：我们将10个特征转换为10个主成分，在处理时间上它们是等效的。

我们还测试了仅使用最后三个PCA组件（第7、8和9组件）的情况，在某些情况下，特别是局部离群因子（LOF）的拟合时间大幅减少。与使用所有10个原始特征（19.4秒）或使用所有10个PCA组件（16.9秒）相比，使用3个组件仅需1.4秒。在所有情况下，除了隔离森林外，拟合时间都有显著下降。

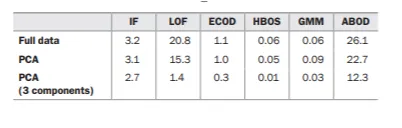
在下表中，我们看到了data_corr数据集的预测时间（另一个测试集的时间也类似）。同样，我们仅使用三个组件时，预测时间大幅下降，尤其是LOF。我们再次看到，两个单变量检测器HBOS和ECOD是最快的之一，尽管在预测的情况下，GMM同样快甚至更快（尽管在拟合时间上稍慢一些）。

对于隔离森林（IF），由于我们无论特征数量如何都训练相同数量的树，并且将所有记录通过相同的一组树进行评估，因此时间不受特征数量的影响。然而，对于此处显示的所有其他检测器来说，特征数量非常重要：与使用所有10个原始特征或所有10个组件相比，使用3个组件时，所有其他检测器的预测时间都显著下降。

在准确性方面，就大多数情况而言，所有五个检测器在两个数据集上都表现良好，它们都将最高的异常值分数分配给了最后一行，而这两个测试数据集的最后一行都是已知的异常值。结果如下表所示。表中有两行，每行对应一个数据集。对于每个数据集，我们展示了每个检测器为已知异常值分配的排名。理想情况下，所有检测器都会为这个异常值分配排名1（即最高的异常值分数）。

在大多数情况下，最后一行实际上被赋予了最高或接近最高的排名，但在第一个数据集上，IF、ECOD和HBOS是例外。这是一个很好的例子，说明即使是像IF这样强大的检测器，有时也会在明显的异常值上表现不佳。

对于第一个数据集，ECOD和HBOS完全没有检测到异常值，但这是预期之中的，因为这个异常值是基于值的组合（它忽略了特征之间的正常线性关系），而单变量检测无法检测到这种异常。第二个数据集的异常值是基于极端值，通常单变量和多变量检测都能够可靠地检测到这种异常，并且在这里也能做到。

在下表中，我们看到了使用PCA处理这些数据集和检测器时准确性的显著提高。这并不总是如此，但在这里确实如此。当检测器在PCA转换后的数据上执行时，所有6个检测器都在两个数据集上将已知异常值排在最高位。当数据经过PCA转换后，各组件之间都是不相关的；异常值就是极端值，这些值更容易识别。

同样有趣的是，仅需最后三个组件就足以将已知异常值排名为顶级异常值，如下表所示。

而且，正如我们之前看到的，在这些情况下，拟合和预测时间大大缩短。这就是使用PCA可以实现显著性能提升的地方：通常只需要使用少量的组件。

仅使用一小组组件还会降低内存需求。这并不一定总是问题，但在处理大型数据集时，这往往是一个重要的考虑因素。

本实验涵盖了数据中可能出现的两种主要类型的异常值：极端值和偏离线性模式的值，这两种异常值都可以在后面的组件中识别出来。在这些情况下，使用最后三个组件效果很好。

使用多少个组件以及使用哪些组件最好可能会有所不同，并且需要进行一些实验（最好使用掺杂数据进行实验来发现）。在某些情况下，使用前面的组件可能更可取（在执行时间、可靠地检测相关异常值以及减少噪声方面），在某些情况下使用中间的组件，而在某些情况下使用后面的组件。正如我们在本文开头的散点图中看到的那样，不同的组件往往会突出不同类型的异常值。

随时间改进异常检测系统

使用PCA组件的另一个有用好处是，它可以更容易地随时间调整异常检测系统。通常，异常检测系统不仅仅在单个数据集上运行一次，而是持续运行，以便不断评估新到达的数据（例如，新的金融交易、传感器读数、网站日志、网络日志等），并且随着时间的推移，我们会更好地了解哪些异常值对我们最相关，以及哪些异常值被低估或高估了。

当使用PCA转换后的数据时，所有报告的异常值都与单个组件相关，因此我们可以看到每个组件报告了多少相关和不相关的异常值。当对每个组件使用简单的单变量测试（如z分数、IQR、IDR、基于MAD的测试以及类似的测试）时，这尤其容易。

随着时间的推移，我们可以学会对与某些组件相关的异常值给予更高的权重，而对其他组件给予更低的权重（取决于我们对假阳性和假阴性的容忍度）。

可视化

降维还有一些优势，它可以帮助我们可视化异常值，特别是当我们将数据降低到二维或三维时。然而，与原始特征一样，即使维度超过三个，我们也可以以直方图的形式逐个查看PCA组件，或者以散点图的形式同时查看两个组件。

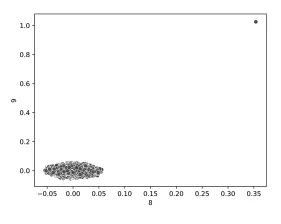
例如，检查第一个测试数据集data_corr（其中包含不寻常的值组合）的最后两个组件时，我们可以清楚地看到已知的异常值，如下所示。然而，这在一定程度上有些值得怀疑，因为这些组件本身难以理解。

结论

本文介绍了 PCA，但还有其他可以类似使用的降维工具，包括 t-SNE（与 PCA 一样，在 scikit-learn 中提供）、UMAP和自动编码器（也在Python 中的异常值检测中介绍）。

本文探讨了使用标准异常检测器（尽管如示例所示，这可以比通常更容易地包括简单的单变量异常检测器）进行异常检测，展示了首先使用PCA转换数据的优势。