当你为分类任务创建神经网络时，你可能是在解决二分类或多分类问题。在后一种情况下，最终层很可能使用的是所谓的Softmax激活函数，该函数会在目标类别上产生一个多类概率分布。

但这个激活函数到底是什么？它是如何工作的？以及，它的工作方式为何使它对于神经网络如此有用？让我们来一探究竟。

在这篇文章中，我们将涵盖所有这些问题。首先，我们将以主要直观的方式了解Softmax的工作原理。然后，我们将阐述当试图解决多分类问题时，它为何对神经网络/机器学习如此有用。最后，我们将通过一个使用Keras创建的示例，向你展示如何在深度学习框架中使用Softmax激活函数。

Softmax是如何工作的？

Softmax总是“在多分类问题中返回目标类别上的概率分布”——这是我在解释Softmax工作原理时经常说的话。

但现在让我们更深入地探讨一下。

“返回概率分布”是什么意思？当我们想要执行多分类任务时，这为何如此有用？

Logits层和Logits

为了解释这一点，我们将不得不看一下神经网络的结构。假设我们有一个神经网络，比如下面这个——非常高层次的变体：

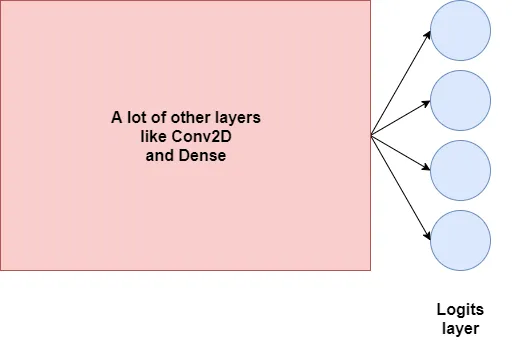
神经网络的最后一层（不包括激活函数）就是我们所说的“logits层”。它仅仅为神经网络提供最终输出。在四类的多分类问题中，这将包含四个神经元——因此，如我们上面所见，有四个输出。

假设这些输出，或我们的logits是：

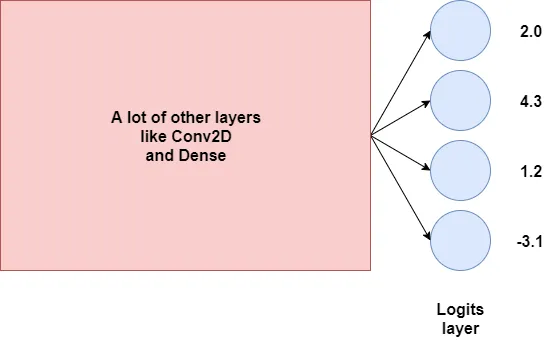
这些输出基本上告诉我们一些关于目标类别的信息，但从上面的输出中，我们还无法理解它们……它们是可能性吗？不是，因为我们不能有负的可能性，对吧？

多分类问题 = 生成概率

然而，在某种程度上，预测某个输入属于哪个目标类别与概率分布有关。对于上面的设置，如果你知道某个值属于四个可能结果中的任何一个的概率，你可以简单地取这些离散概率的argmax（即最大值的索引），并找到类别结果。因此，如果我们能够将上面的logits转换为概率分布，那就太好了——我们就达到目的了！

让我们进一步探索这个想法。

如果我们真的想将logits转换为概率分布，我们首先需要看看概率分布是什么。

柯尔莫哥洛夫公理

我记得在大学上概率论课时，概率论作为一个整体可以通过其基础来描述，即所谓的概率公理或柯尔莫哥洛夫公理。它们以安德烈·柯尔莫哥洛夫的名字命名，他在1933年引入了这些公理。

它们如下：

• 某事件发生的概率，即事件，是一个非负实数。
• 分布中至少有一个事件发生的概率是1，即所有单个概率的和是1。
• 一系列互斥集发生的概率等于各个集概率的和。

现在，第三个公理对于今天的文章来说并不是很有趣，但前两个是。

从它们可以推断出，某事件发生的几率必须是一个正实数，例如0.238。由于概率的和必须等于1，所以任何概率都不能大于1。因此，任何概率都位于[0, 1]的范围内。

好吧，我们可以接受这一点。然而，在我们探索将logits转换为多类概率分布的可能方法之前，还有一个解释需要说明：离散概率分布和连续概率分布之间的区别。

离散分布与连续分布

为了加深对上述问题的理解，我们需要看看离散概率分布和连续概率分布之间的区别。

根据维基百科（2001），这是离散概率分布：

离散概率分布是可以取可数数值的概率分布。
维基百科（2001）：离散概率分布

另一方面，连续概率分布是：

连续概率分布是具有绝对连续累积分布函数的概率分布。
维基百科（2001）：连续概率分布

因此，虽然离散分布可以取一定数量的值——比如四个——并且因此相当“块状”，每个值有一个概率，但连续分布可以取任何值，并且概率表示为在某个范围内。

走向离散概率分布

你可能已经注意到，我已经给出了关于上述神经网络是否受益于将logits转换为离散分布还是连续分布的答案。

显然，答案是离散概率分布。

对于每个结果（每个神经元代表一个目标类的结果），我们想知道各个概率，但它们当然必须与机器学习问题中的其他目标类相关。因此，概率分布，特别是离散概率分布，是可行的道路！

但我们如何将logits转换为概率分布呢？我们使用Softmax！

Softmax函数

Softmax函数允许我们将输入表示为离散概率分布。数学上，它定义如下：

直观地来说，这可以定义如下：对于我们输入向量中的每个值（即输入），Softmax 值是该单独输入的指数除以所有输入指数之和。

这确保了以下几件事情的发生：

• 由于指数函数的作用，负输入将被转换为非负值。
• 每个输入都将位于（0, 1）区间内。
• 由于每个Softmax计算中的分母都是相同的，因此这些值相互成比例，从而确保它们加起来等于1。

这反过来使我们能够“将它们解释为概率”（维基百科，2006）。较大的输入值对应于较大的概率，且这种对应关系是呈指数级的，这同样归因于指数函数。

现在，让我们回到之前概述的初始场景。

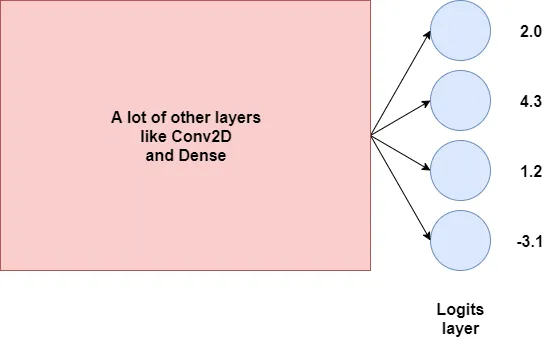
我们现在可以将逻辑值（logits）转换为离散概率分布：

逻辑值：2.0

Softmax 计算：

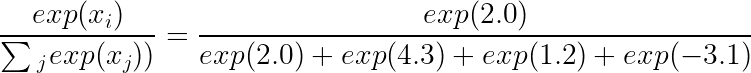
Softmax 输出：0.087492

逻辑值：4.3

Softmax 计算：

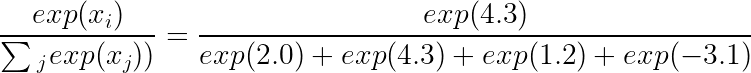
Softmax 结果：0.872661

逻辑值：1.2

Softmax 计算：

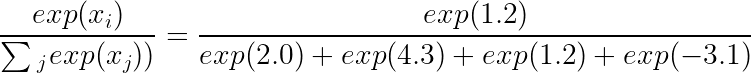
逻辑值：-3.1

Softmax 计算：

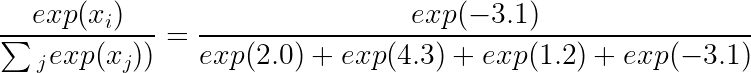
总和：0.99757

（四舍五入后）：1

现在，我们来检查上述结果是否遵循我们之前讨论过的柯尔莫哥洛夫概率公理，以验证它是否确实是一个有效的概率分布。

1. 每个概率必须是一个非零实数。这对于我们的结果是成立的：每个结果都是实数值，且非零。
2. 概率的总和必须为1。这对于我们的结果也是成立的：由于实数的性质，截断值的总和约为1。实际总和为1。

事实上，在我们的逻辑值（logits）场景中，任何输入都会满足这些条件。首先，任何输入的分母都是相同的，因此它们被归一化到（0, 1）范围内，总和为1。此外，我们可以看到，由于指数函数的性质，当任何输入被输入到Softmax函数时，确实会产生一个非零实数：

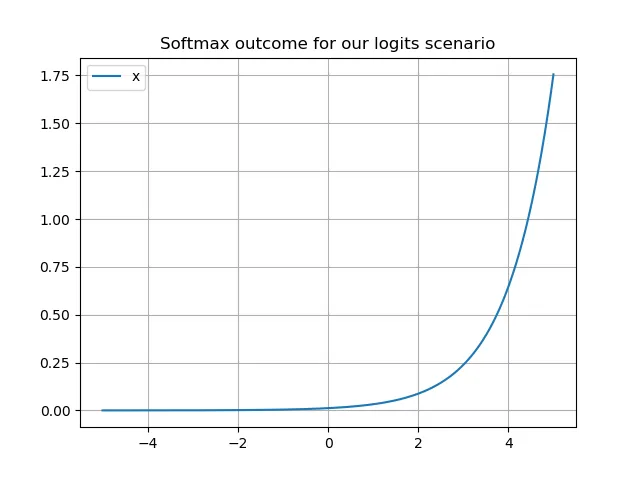
这也解释了为什么我们的逻辑值（logit）= 4.3 会产生如此大的概率 p ≈ 0.872661。

这意味着：太好了，我们可以使用Softmax来生成概率分布！

为什么神经网络中使用Softmax

如果我们想找出Softmax对神经网络如此有用的原因，我们需要考虑三个方面。

首先，我们需要探索为什么我们不能直接使用argmax，而是要用Softmax来近似其结果。

然后，我们要看看使用指数函数相比传统归一化的好处，以及使用欧拉常数作为指数底数的好处。

最后，我们将找出这对优化过程意味着什么，以及为什么这正是我们从神经网络中想要得到的。

为什么不直接使用argmax？

回忆一下，我们有一个神经网络，其中有一个逻辑值（logits）层，其输出为：

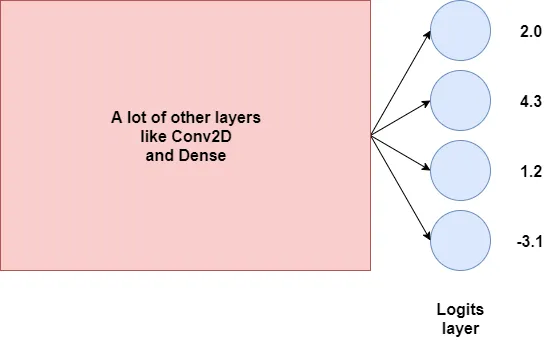
如果你今天思考得非常严谨，你可能会想：为什么我们不直接把argmax值作为激活函数呢？它不是能提供相同的结果吗？

也就是说，如果x = [2.0, 4.3, 1.2, -3.1]是某个argmax函数的输入，那么输出将是[0, 1, 0, 0]。这很好，因为我们现在有了输出值！

但这是正确的吗？

我们不知道，因为我们不知道输入是什么。如果我们知道，就可以检查。

现在假设我们输入了一张应该属于第4类的图像。这就有问题了，因为我们的输出是[0, 1, 0, 0]——也就是第2类！

我们需要改进！

在神经网络中，默认情况下，会使用像梯度下降或自适应优化器这样的优化技术。对于每个可训练的参数，反向传播会计算损失值和中间层相对于该参数的梯度，然后优化器会相应地调整该参数的权重。

但这要求函数是可微的。而argmax不是，或者即使它是，也没用（Shimis，nd）。因为argmax函数的梯度在几乎所有地方都是零（如果你稍微移动一下argmax函数上的点，输出将保持不变），或者甚至是未定义的，因为argmax不是连续的（Shimis，nd）。因此，在使用基于梯度下降的优化方法训练神经网络时，不能使用argmax。

Softmax除了具有我们之前看到的归一化的良好性质外，还是可以微分的。因此，它对于优化神经网络非常有用。

现在，你可能会想：好吧，我相信我不能使用argmax。但为什么我必须使用Softmax呢？为什么我不能只进行没有指数的归一化（Vega，nd）？

指数的好处

也就是说，而不是写……

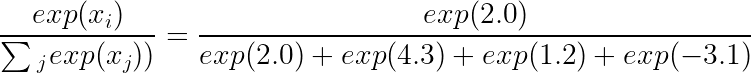
……你可能会想写成……

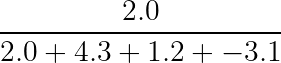
这完全有道理，但现在让我们来看看我们希望输出是什么样子的。尽管我们并不直接使用argmax，但我们是不是还是希望输出能像argmax那样，让实际的类别排在最前面？

现在来看看我们的逻辑值（logits）。

如果使用argmax，它们会转换成：

Logit value | Argmax computation            | Argmax outcome
     2.0    |  argmax(2.0,4.3,1.2,-3.1)     | [0,1,0,0]
     4.3    |  argmax(2.0,4.3,1,2,-3,1)     | [0,1,0,0]
     1.2    |  argmax(2.0,4.3,1.2,-3.1)     | [0,1,0,0]
    -3.1    |  argmax(2.0,4.3,1.2,-3,1)     | [0,1,0,0]

正如我们之前看到的，Softmax 将我们的逻辑值（logits）转换成了 [0.09, 0.87, 0.04, 0.00]，这非常接近实际结果！

但是，如果使用“普通”的或没有指数的除法，会发生什么呢？

Logit value | Regular division              | Argmax outcome
      2.0   | 2.0/(2.0 + 4.3 + 1.2 + -3.1)  | 0.454
      4.3   | 4.3/(2.0 + 4.3 + 1.2 + -3.1)  | 0.978
      1.2   | 1.2/(2.0 + 4.3 + 1.2 + -3.1)  | 0.273
     -3.1   | -3.1/(2.0 + 4.3 + 1.2 + -3.1) | -0.704 ??

正如我们所见，这些值不再有意义，甚至不再遵循 Kolmogorov 公理来表示一个有效的概率分布！

因此，我们使用Softmax。

现在，最后一个问题：为什么我们在Softmax中使用自然对数的底数e？为什么我们不使用一个常数，比如f(x) = 3x？

这与导数有关（Vega，未注明年份；CliffsNotes，nd）：

• 对于f(x) = ex。
• 对于f(x) = ax。

因此，e^x的导数更加简洁，因此更受欢迎。

最大化类别结果的逻辑值

好的。我们可以使用Softmax来生成由logits层中的神经元表示的目标类别上的离散概率分布。

现在，在我们使用Keras构建示例模型之前，是时候暂时停下来思考一下优化过程中会发生什么。

你可能已经知道，在高级监督机器学习过程中的前向传播中，训练数据被输入到模型中。预测结果与真实值（即目标）进行比较，并最终汇总成一个损失值。基于这个损失值，反向传播计算改进的梯度，然后优化器根据其特性执行这种改进。这个迭代过程在模型表现良好时停止。

到目前为止一切顺利，但当你设计一个具有num_classes个输出神经元以及一个Softmax层的神经网络时会发生什么？

从实用性的角度来看，重要的是要理解你的模型很可能会学会将某些类别映射到某些逻辑值上，即它学会了为某些类别结果最大化某些逻辑值。这样做，训练过程实际上学会了将输入“引导”到输出，从而生成一个实际有用的机器学习模型。

这是很好的：对于来自某个类别的新输入，类别结果等于真实值的几率增加了。这是Softmax对神经网络如此有用的另一个原因，加上之前提到的其他原因。

使用Keras的Softmax示例

现在，让我们从理论转向实践——我们要开始编码了！

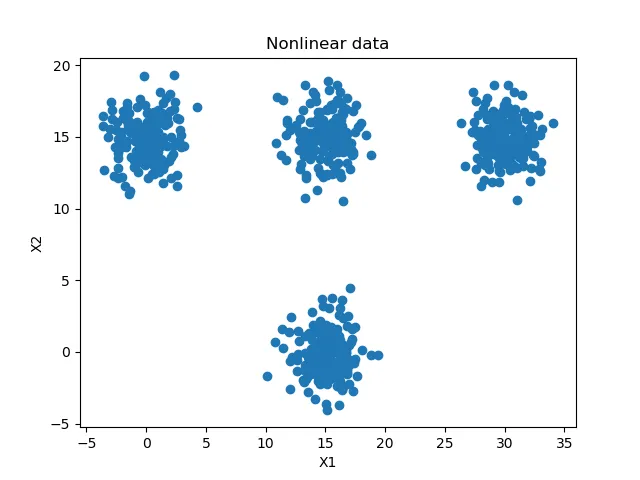
事实上，我们将使用Keras编写一个示例模型，该模型利用Softmax函数进行分类。更具体地说，它将是一个密集连接的神经网络，将学习将样本分类为四个类别中的一个。幸运的是（也是有意为之的），训练数据（我们将在过程中生成）在二维空间中是可分离的，尽管不是线性可分的。

是时候打开你的编辑器开始编码了！

首先，我们将定义一些导入：

'''
  Keras model to demonstrate Softmax activation function.
'''
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import to_categorical
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs

最重要的是，我们使用Keras及其一些模块来构建模型。在底层，它将基于Tensorflow运行。此外，我们还将导入Matplotlib的Pyplot库用于数据可视化，Numpy用于数值处理，以及Scikit-learn用于生成数据。

因此，在运行此模型之前，请确保你已安装这些依赖项。最简单的方法是使用pip install命令进行安装：

pip install keras tensorflow matplotlib numpy scikit-learn

模型配置

接下来是模型配置部分。我们在这里定义了将生成多少个样本，其中有多少用于测试训练后的模型（250个），我们的聚类在二维空间中的位置，有多少个聚类，以及要使用哪种损失函数（确实，由于我们在最后一层使用了Softmax激活函数，因此选择使用分类交叉熵损失）。

# Configuration options
num_samples_total = 1000
training_split = 250
cluster_centers = [(15,0), (15,15), (0,15), (30,15)]
num_classes = len(cluster_centers)
loss_function_used = 'categorical_crossentropy'

生成数据

在配置好模型之后，接下来就是生成一些数据了。我们为此使用Scikit-Learn的make_blobs函数，它允许我们生成如上图所示的样本聚类。我们根据配置来生成这些数据，即基于聚类中心、总共要生成的样本数量以及我们想要的类别数量。

# Generate data
X, targets = make_blobs(n_samples = num_samples_total, centers = cluster_centers, n_features = num_classes, center_box=(0, 1), cluster_std = 1.5)
categorical_targets = to_categorical(targets)
X_training = X[training_split:, :]
X_testing = X[:training_split, :]
Targets_training = categorical_targets[training_split:]
Targets_testing = categorical_targets[:training_split].astype(np.integer)

数据生成后，我们可以将目标转换成独热编码（one-hot encoded）向量，以便使它们与分类交叉熵损失函数兼容。最后，我们将数据分为训练集和测试集。

完成这些后，我们就可以设置输入数据的形状了，因为我们现在已经知道了它的形状。

# Set shape based on data
feature_vector_length = len(X_training[0])
input_shape = (feature_vector_length,)
print(f'Feature shape: {input_shape}')

我们也可以生成你之前看到的可视化内容。

plt.scatter(X_training[:,0], X_training[:,1])
plt.title('Nonlinear data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()

模型架构

现在我们已经导入了所需的依赖项并配置了模型，是时候定义其架构了。

这将是一个非常简单的架构，确切地说，是一个全连接网络。它将包含三层，其中一层是输出层。第一层接收形状为input_shape的数据，通过ReLU激活函数进行激活，因此需要使用He权重初始化。它的输出形状是(12, )。

第二层的工作原理类似，但输出形状是(8, )。

最后一层是我们的输出层，它学习num_classes个输出。在我们的案例中，num_classes = 4，这与我们在整篇博客中讨论的场景相一致。此外，与ReLU激活函数不同，它使用Softmax激活函数，因此我们将得到一个多类的概率分布！

# Create the model
model = Sequential()
model.add(Dense(12, input_shape=input_shape, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(8, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(num_classes, activation='softmax'))

编译、数据拟合和评估

随后，我们可以根据之前配置的损失函数以及想要使用的优化器来编译（即配置）模型，并设置额外的评估指标（由于对人类来说直观易懂，所以选择准确率）。

然后，我们将训练数据拟合到模型中，训练30次迭代（周期），并使用5的批量大小。20%的训练数据将用于验证目的，并且由于将详细模式设置为True，所有输出都将显示在屏幕上。

# Configure the model and start training
model.compile(loss=loss_function_used, optimizer=keras.optimizers.adam(lr=0.001), metrics=['accuracy'])
history = model.fit(X_training, Targets_training, epochs=30, batch_size=5, verbose=1, validation_split=0.2)
# Test the model after training
test_results = model.evaluate(X_testing, Targets_testing, verbose=1)
print(f'Test results - Loss: {test_results[0]} - Accuracy: {test_results[1]*100}%')

数据拟合完成后，就是测试模型的时候了。我们通过model.evaluate方法来实现，将测试数据输入其中。结果会显示在屏幕上。

完整模型代码

'''
  Keras model to demonstrate Softmax activation function.
'''
import keras
from keras.models import Sequential
from keras.layers import Dense
from keras.utils import to_categorical
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_blobs
# Configuration options
num_samples_total = 1000
training_split = 250
cluster_centers = [(15,0), (15,15), (0,15), (30,15)]
num_classes = len(cluster_centers)
loss_function_used = 'categorical_crossentropy'
# Generate data
X, targets = make_blobs(n_samples = num_samples_total, centers = cluster_centers, n_features = num_classes, center_box=(0, 1), cluster_std = 1.5)
categorical_targets = to_categorical(targets)
X_training = X[training_split:, :]
X_testing = X[:training_split, :]
Targets_training = categorical_targets[training_split:]
Targets_testing = categorical_targets[:training_split].astype(np.integer)
# Set shape based on data
feature_vector_length = len(X_training[0])
input_shape = (feature_vector_length,)
print(f'Feature shape: {input_shape}')
# Generate scatter plot for training data
plt.scatter(X_training[:,0], X_training[:,1])
plt.title('Nonlinear data')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# Create the model
model = Sequential()
model.add(Dense(12, input_shape=input_shape, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(8, activation='relu', kernel_initializer='he_uniform'))
model.add(Dense(num_classes, activation='softmax'))
# Configure the model and start training
model.compile(loss=loss_function_used, optimizer=keras.optimizers.adam(lr=0.001), metrics=['accuracy'])
history = model.fit(X_training, Targets_training, epochs=30, batch_size=5, verbose=1, validation_split=0.2)
# Test the model after training
test_results = model.evaluate(X_testing, Targets_testing, verbose=1)
print(f'Test results - Loss: {test_results[0]} - Accuracy: {test_results[1]*100}%')

结果

运行后，你应该会发现一个表现极好的模型（这是有道理的，因为数据是可以非线性分离的，而我们的模型具备这种能力）：

Test results - Loss: 0.002027431168593466 - Accuracy: 100.0%

当然，在实际应用中，你的机器学习模型将会更加复杂——数据也同样会更加复杂——但这并不是本博客文章的目的。相反，除了理论学习Softmax之外，你现在也已经看到了如何在实际中应用它。

总结

本文章围绕Softmax激活函数展开。它是什么？它是如何工作的？为什么它对神经网络有用？以及我们如何使用Keras在实践中实现它？这些问题就是我们所要回答的。

在此过程中，我们了解到Softmax是一种激活函数，它将输入（可能是逻辑值，即在神经网络最后一层应用激活函数之前的输出）转换为目标类别上的离散概率分布。Softmax确保概率分布的标准得到满足——即概率是非负实数，且概率之和等于1。这很棒，因为我们现在可以创建模型，这些模型学习为属于特定类的输入最大化逻辑输出，从而也最大化概率分布。简单地取argmax值就可以让我们选择类别预测，例如在对象检测器、图像分类器和文本分类器中将其显示在屏幕上。