定义

梯度提升是一种集成机器学习技术，它构建了一系列决策树，每棵树都旨在纠正前一棵树的错误。与采用浅树的AdaBoost不同，梯度提升使用较深的树作为其弱学习器。每棵新树都专注于最小化残差（即实际值与预测值之间的差异）而不是直接从原始目标中学习。

对于回归任务，梯度提升通过逐一添加树木的方式，训练每棵新树以减少通过解决当前残差而留下的剩余错误。最终预测是通过将所有树的输出相加得出的。

该模型的强大之处在于其加性学习过程，虽然每棵树都专注于纠正集成中剩余的错误，但这种顺序组合创造了一个强大的预测器，它通过专注于模型仍然难以应对的问题部分，逐步降低整体预测误差。

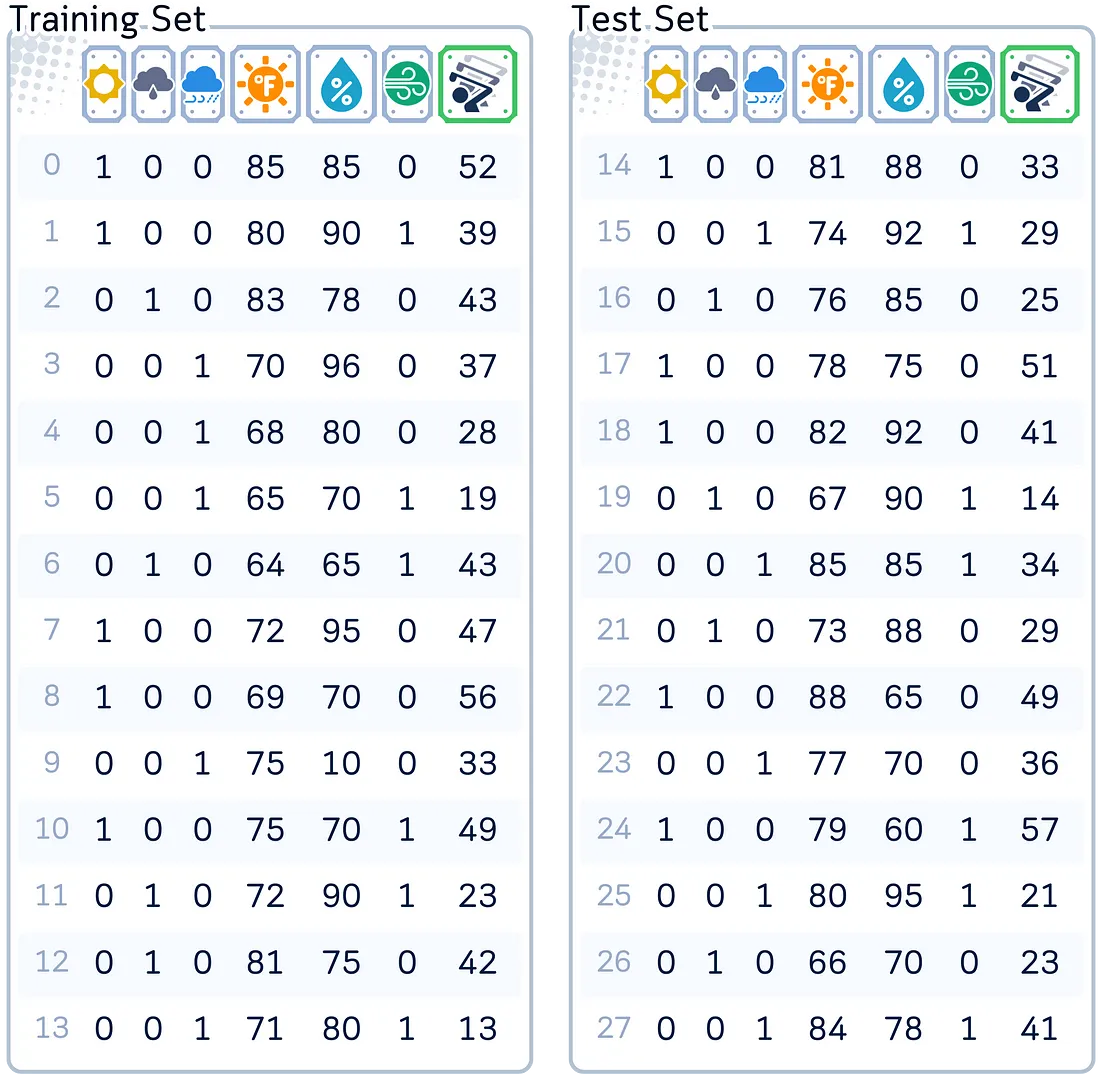
使用的数据集

在本文中，我们将重点关注经典高尔夫数据集作为回归的示例。虽然梯度提升可以有效地处理回归和分类任务，但我们将专注于更简单的任务，在本例中是回归——根据天气状况预测将打高尔夫球的球员人数。

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
# Create dataset
dataset_dict = {
   'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 
               'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain',
               'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast',
               'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
   'Temp.': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,
             72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,
             88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
   'Humid.': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,
              90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,
              65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
   'Wind': [False, True, False, False, False, True, True, False, False, False, True,
            True, False, True, True, False, False, True, False, True, True, False,
            True, False, False, True, False, False],
   'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29,
                   25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
# Prepare data
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='')
df['Wind'] = df['Wind'].astype(int)
# Split features and target
X, y = df.drop('Num_Players', axis=1), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)

主要机制

梯度提升的工作原理如下：

1. 初始化模型：首先进行一个简单的预测，通常取目标值的均值。
2. 迭代学习：对于设定好的迭代次数，计算残差，训练一棵决策树来预测这些残差，并将新树的预测结果（按学习率缩放后）累加到当前总和上。
3. 在残差上构建树：每棵新树都专注于所有先前迭代中剩余的错误。
4. 最终预测：将所有树的贡献（按学习率缩放后）与初始预测相加，得出最终预测结果。

训练步骤

我们将遵循标准的梯度提升方法：

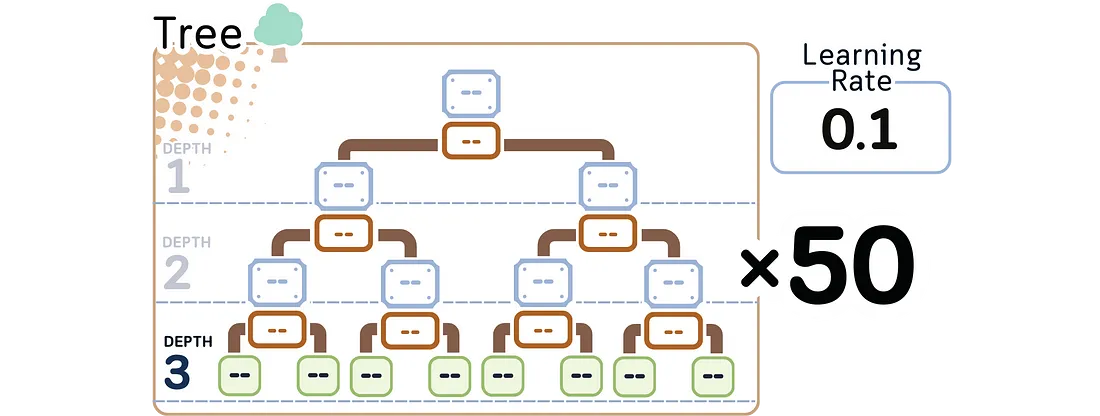
1.0. 设置模型参数：

在构建任何树之前，我们需要设置控制学习过程的核心参数：

· 要顺序构建的树的数量（通常为100棵，但我们将选择50棵），

· 学习率（通常为0.1），以及

· 每棵树的最大深度（通常为3）。

第一棵树

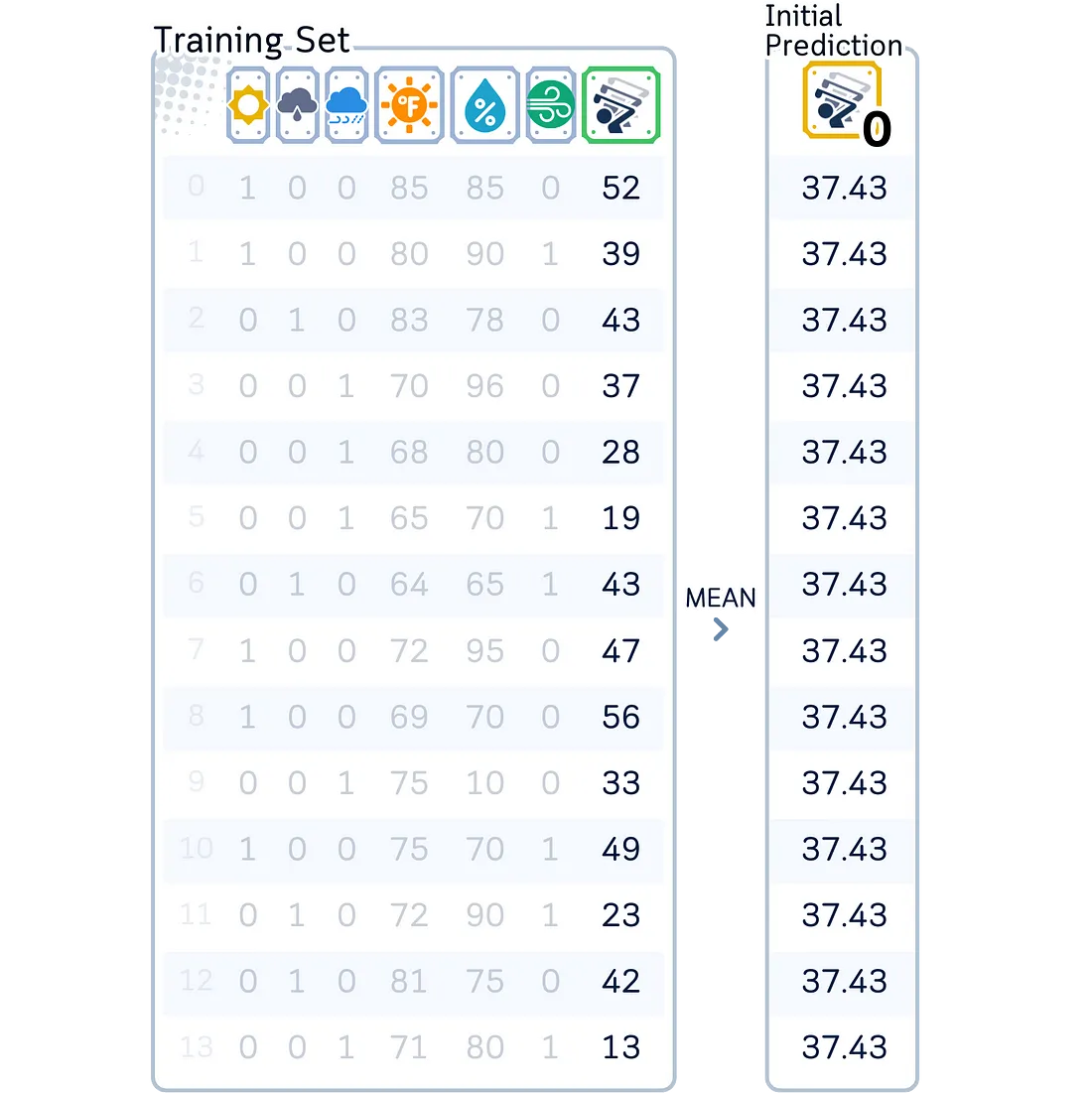
2.0 对标签进行初始预测。这通常是取均值（就像一个简单的预测一样）。

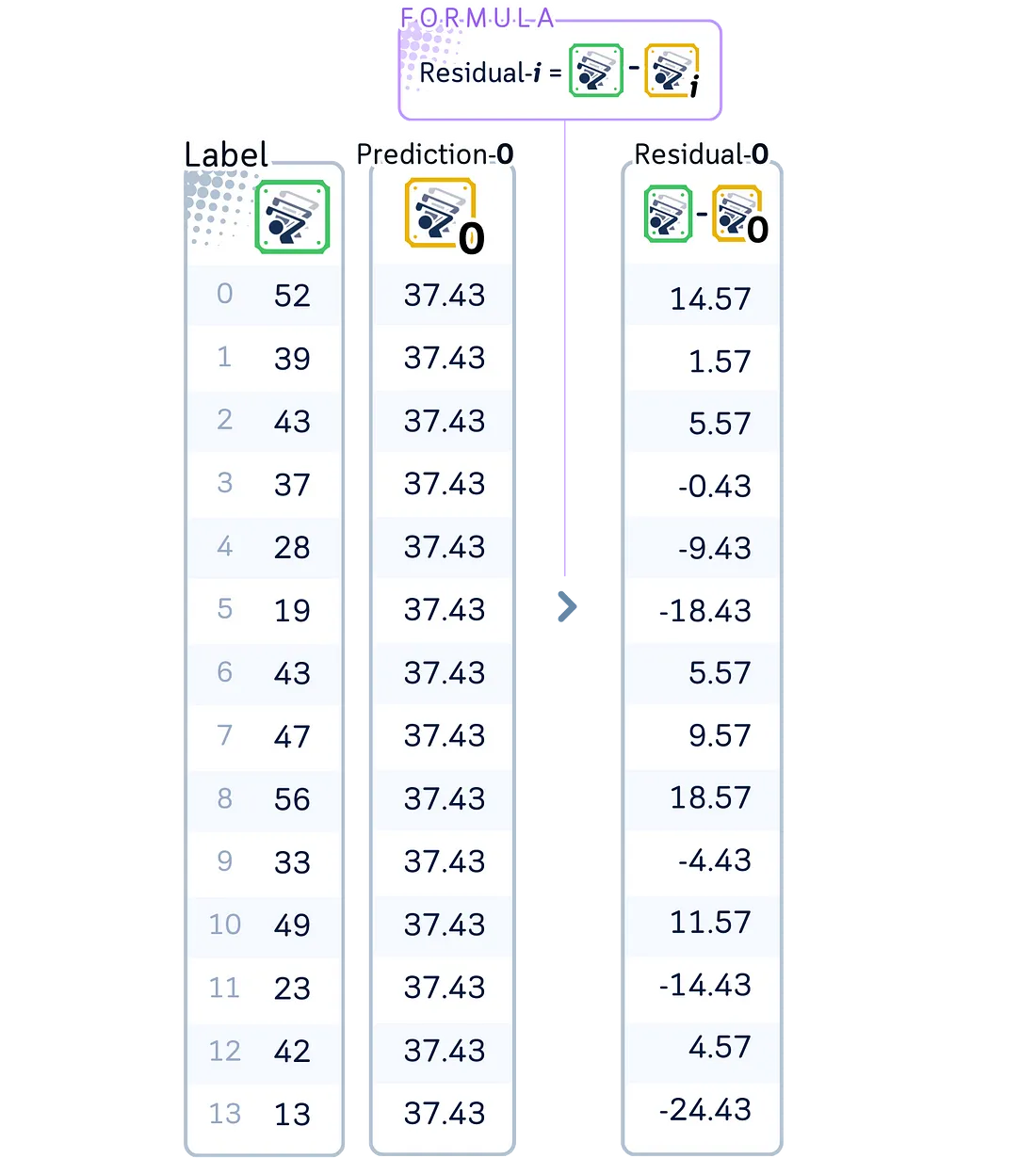
2.1. 计算临时残差（或伪残差）：

残差 = 实际值-预测值

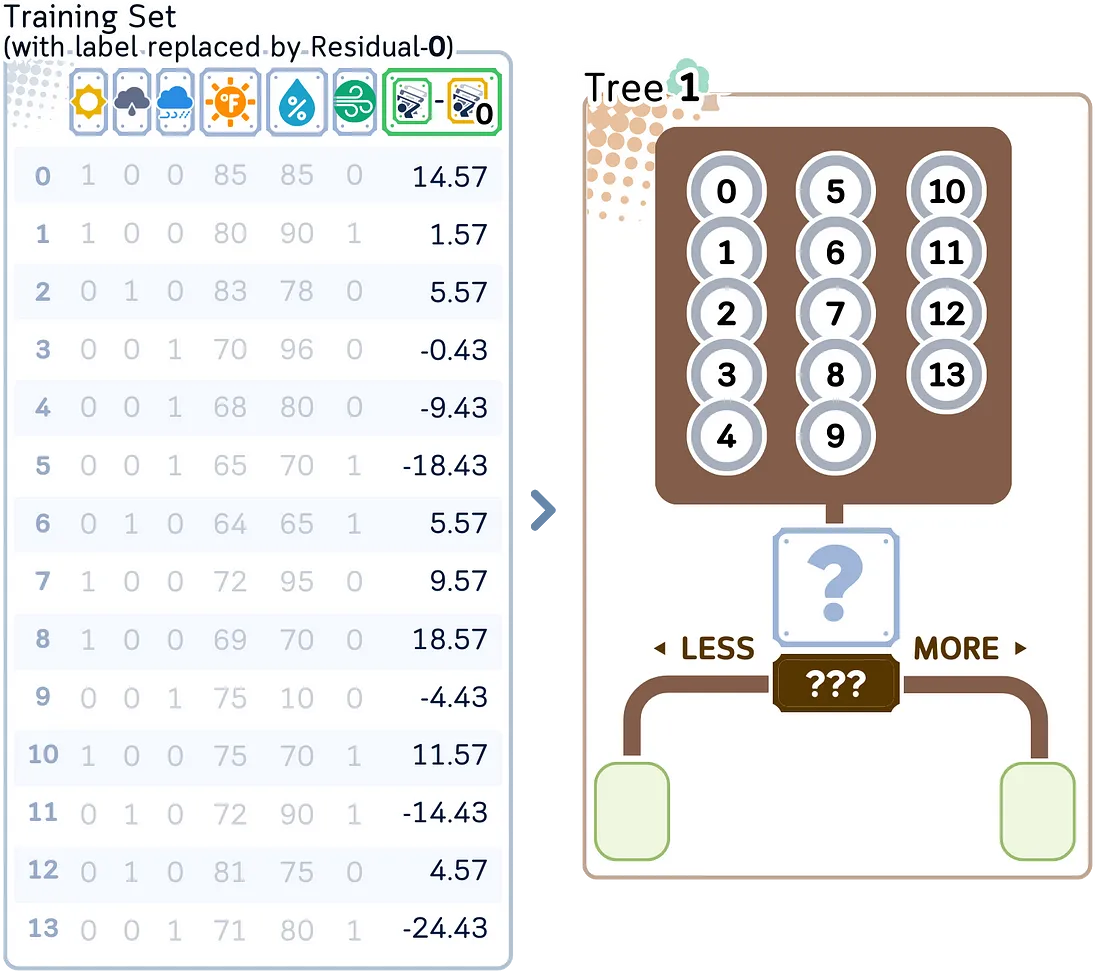
2.2. 构建一棵决策树来预测这些残差。构建树的步骤与回归树中的步骤完全相同。

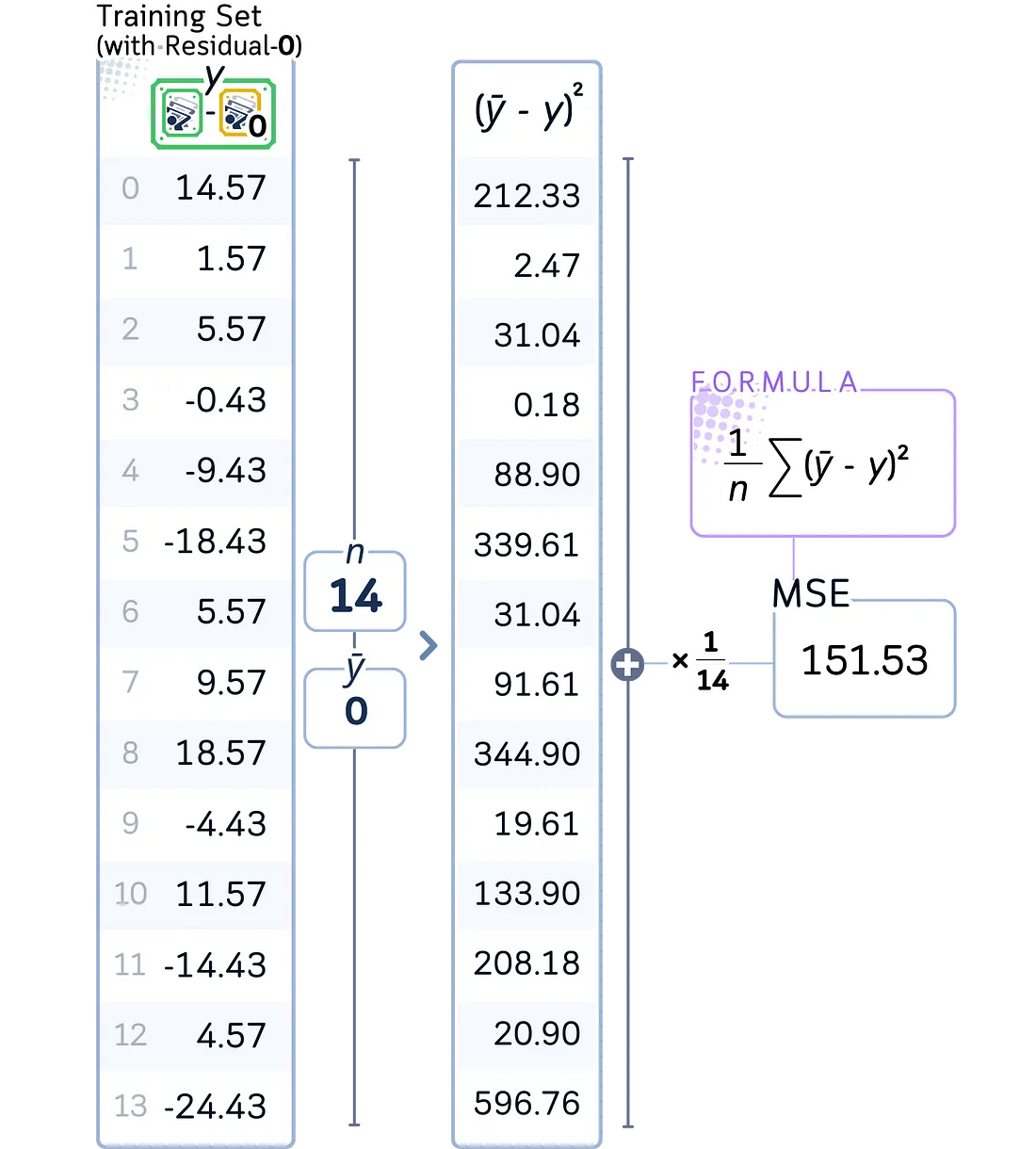
a. 计算根节点的初始 MSE（均方误差）

b. 对于每个特征：

· 根据特征值对数据进行排序。

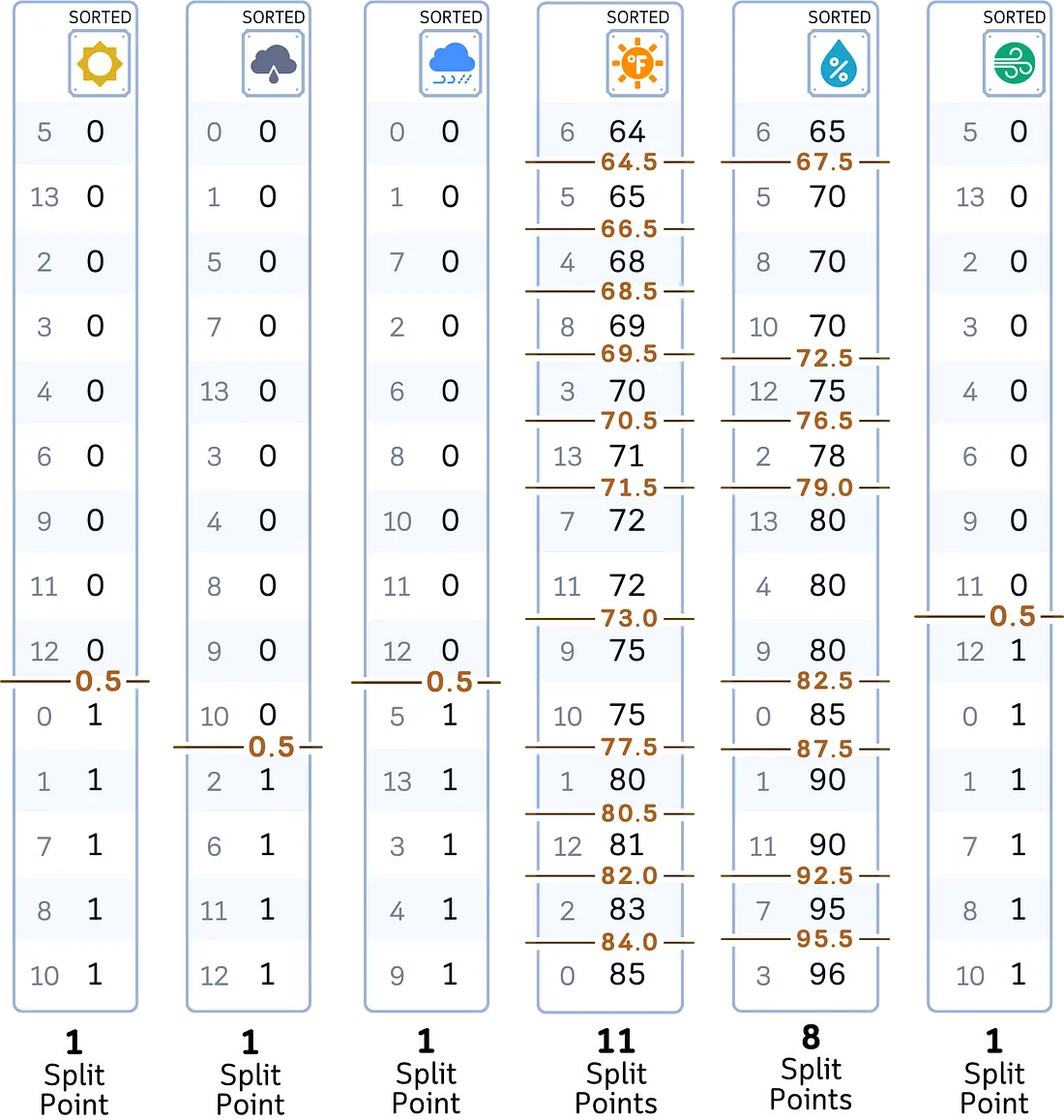
· 对于每个可能的分割点：

·· 将样本分为左组和右组

·· 计算两组的均方误差（MSE）

·· 计算此次分割的MSE减少量

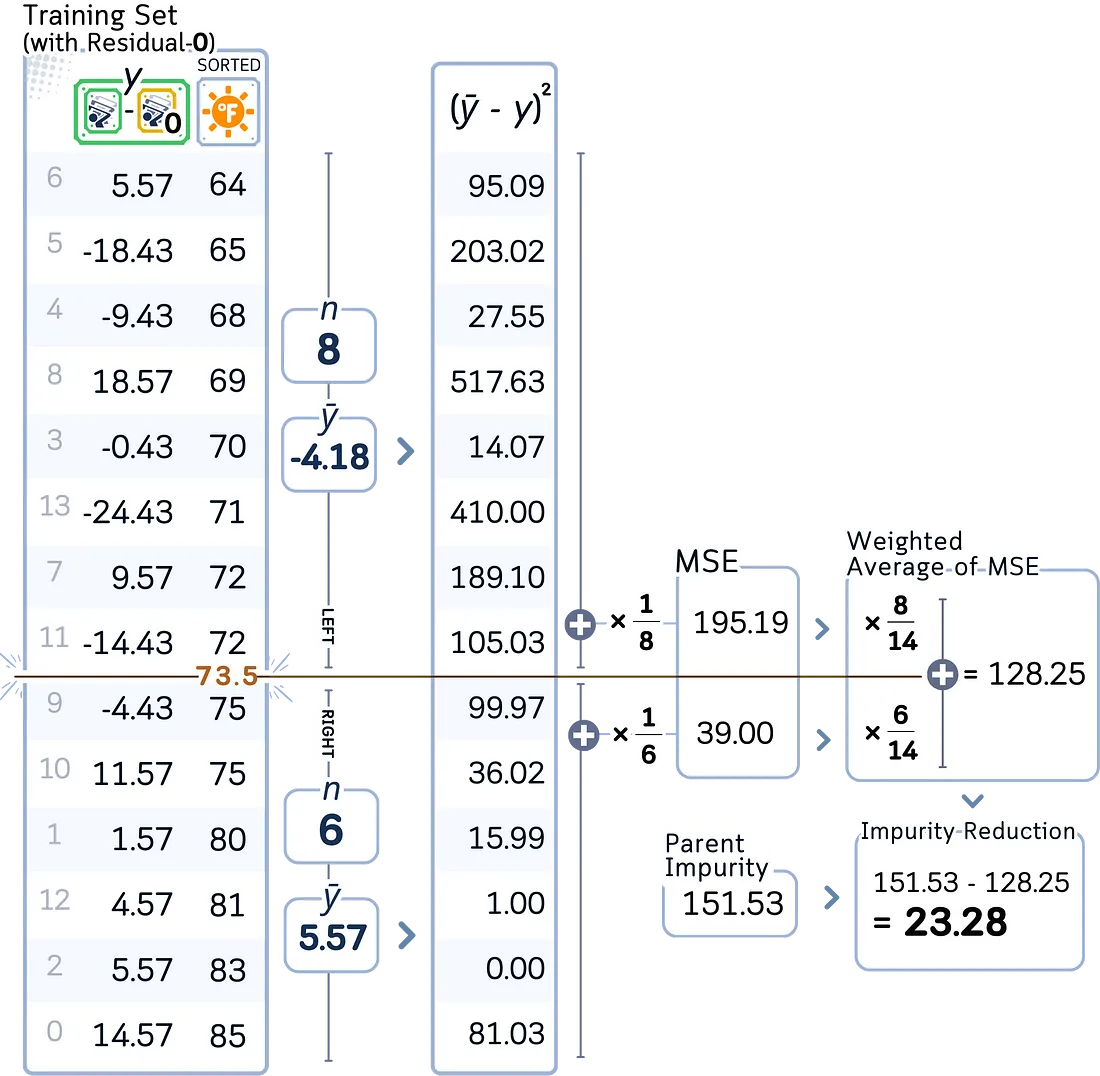
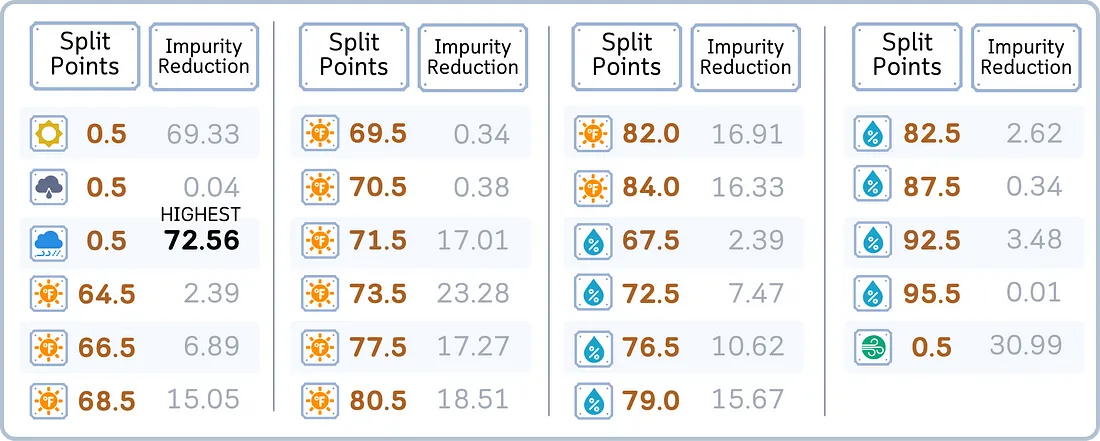
c. 选择能带来最大均方误差（MSE）减少量的分割方式。

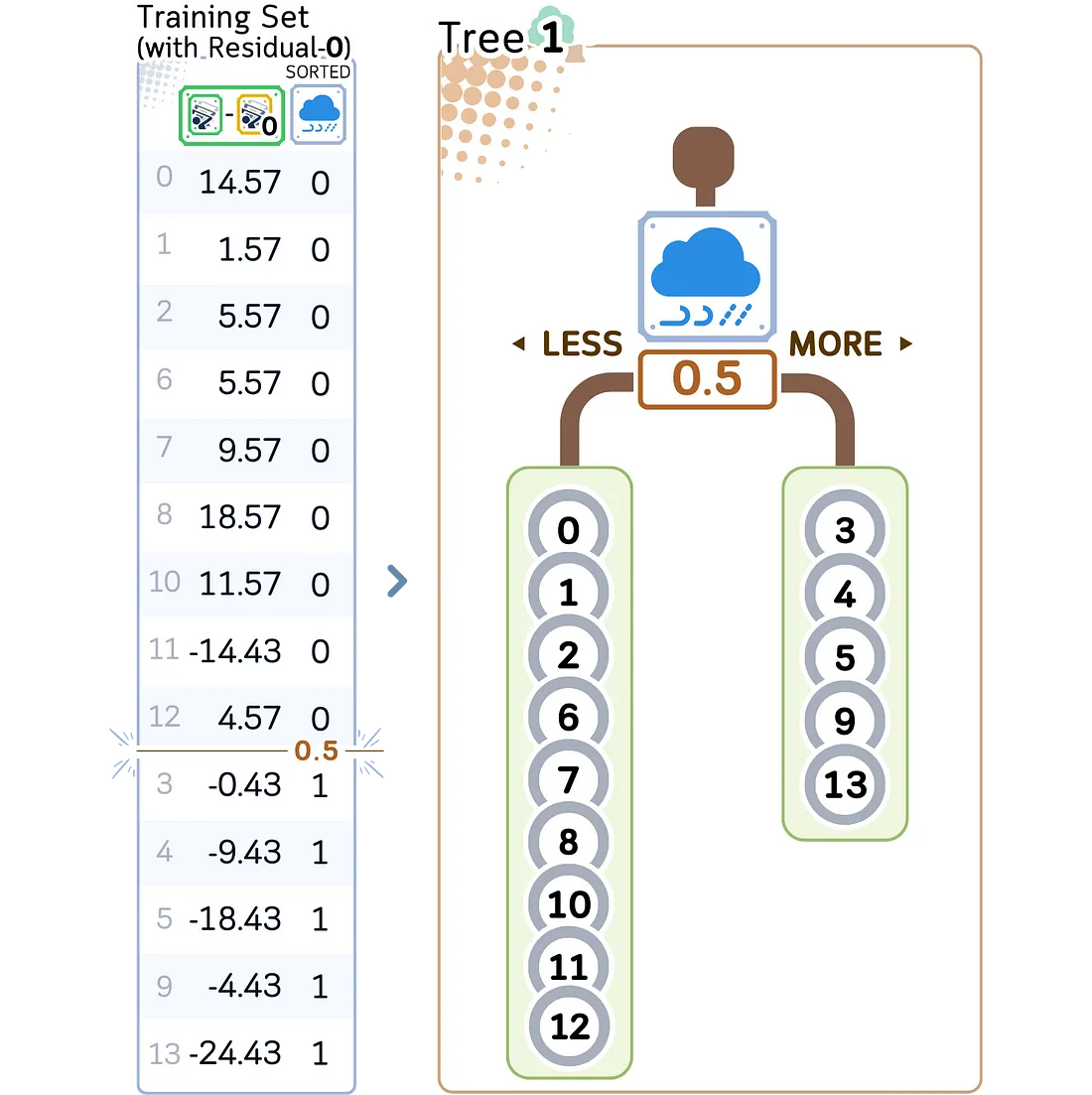
d. 继续分裂，直到达到最大深度或每片叶子的最小样本数。

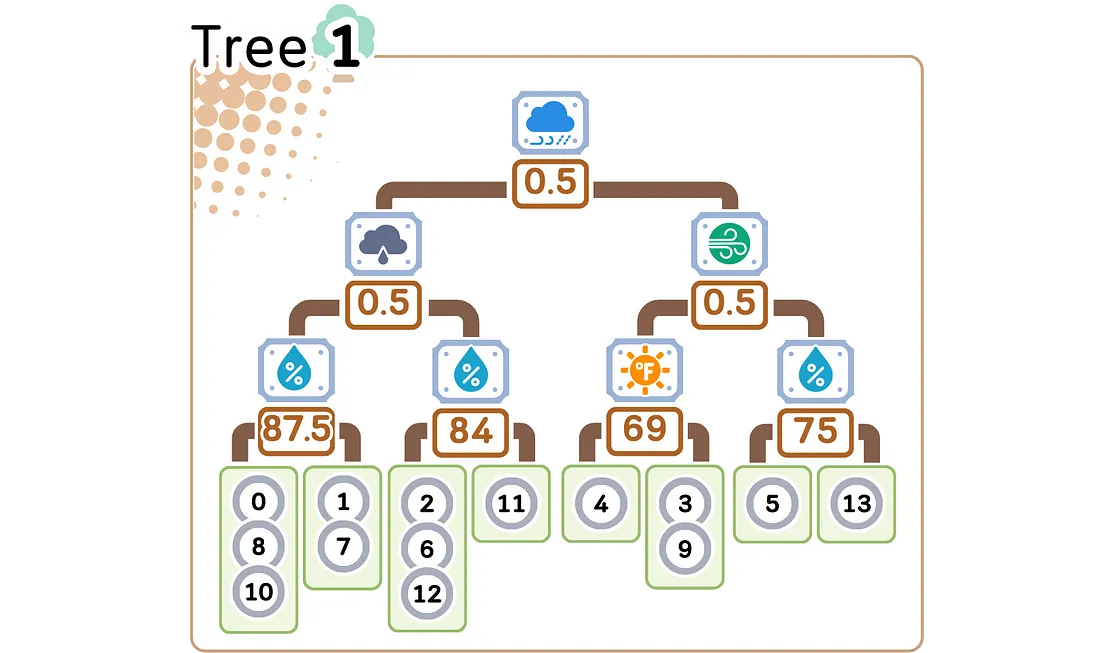
2.3. 计算叶值

对于每个叶子，找到残差的平均值。

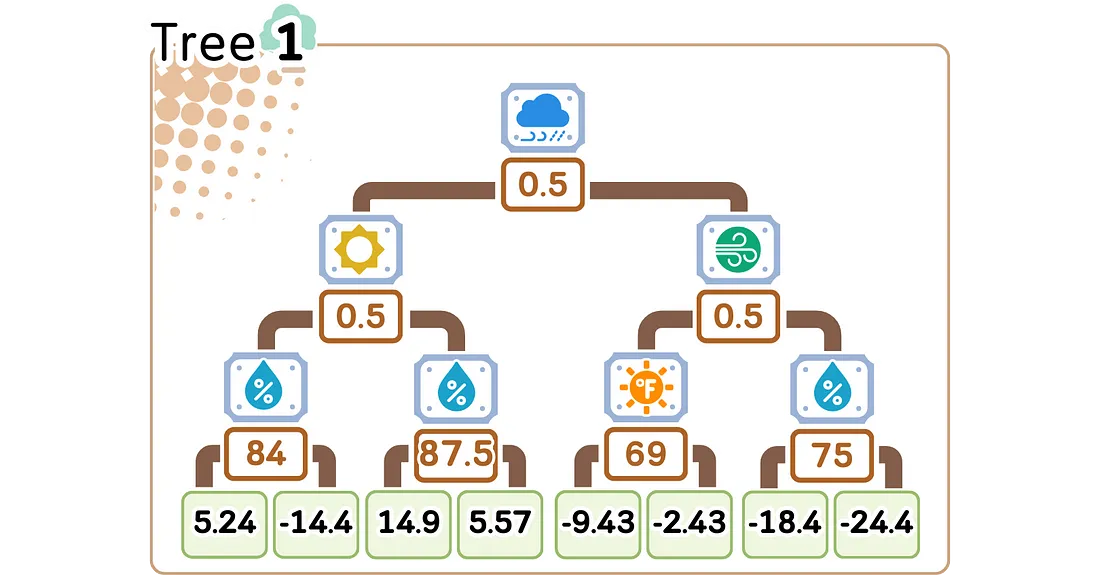
2.4. 更新预测

· 对于训练数据集中的每个数据点，根据新树确定它落入哪个叶节点。

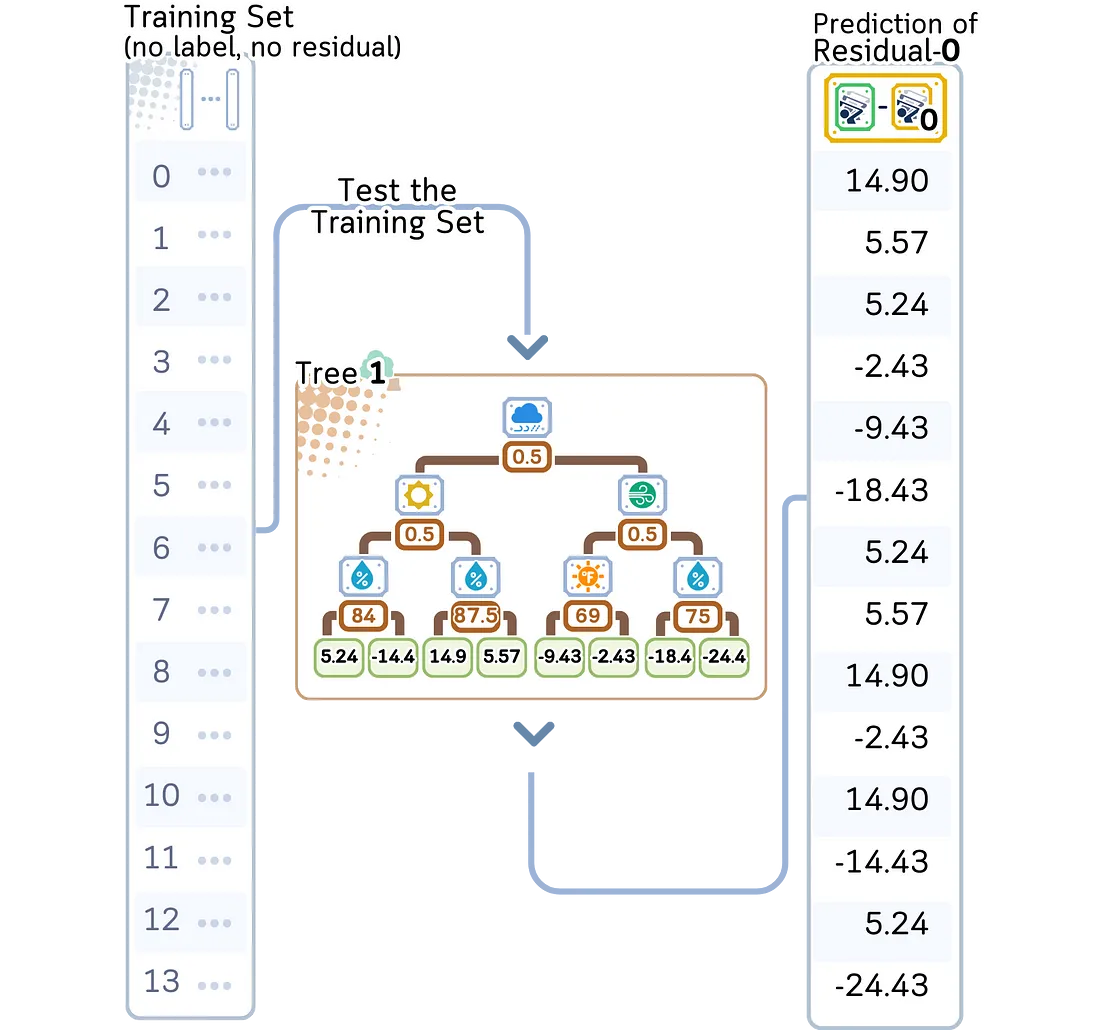
· 将新树的预测结果乘以学习率，并将这些缩放后的预测结果添加到当前模型的预测中。这将是更新后的预测。

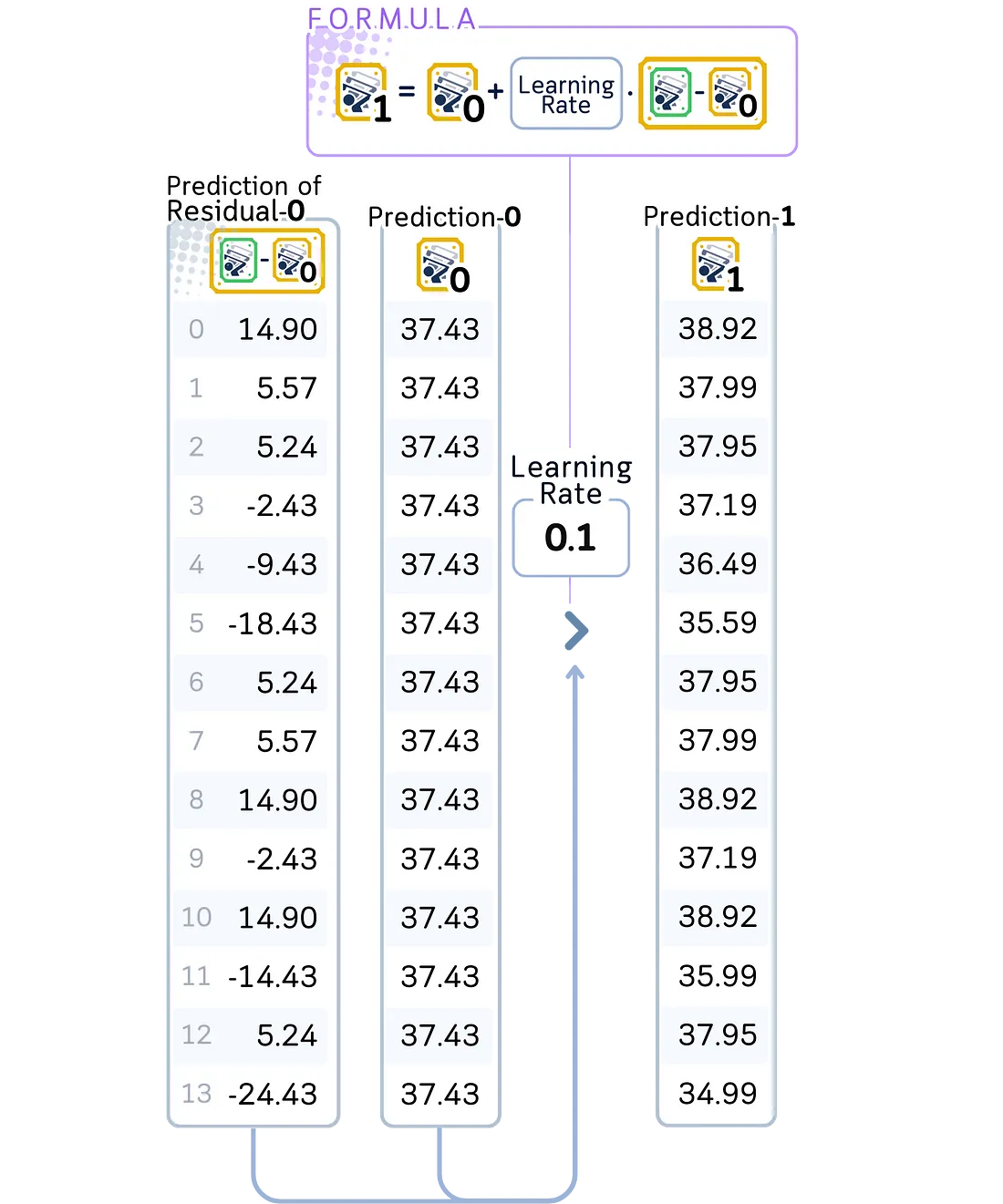
第二棵树

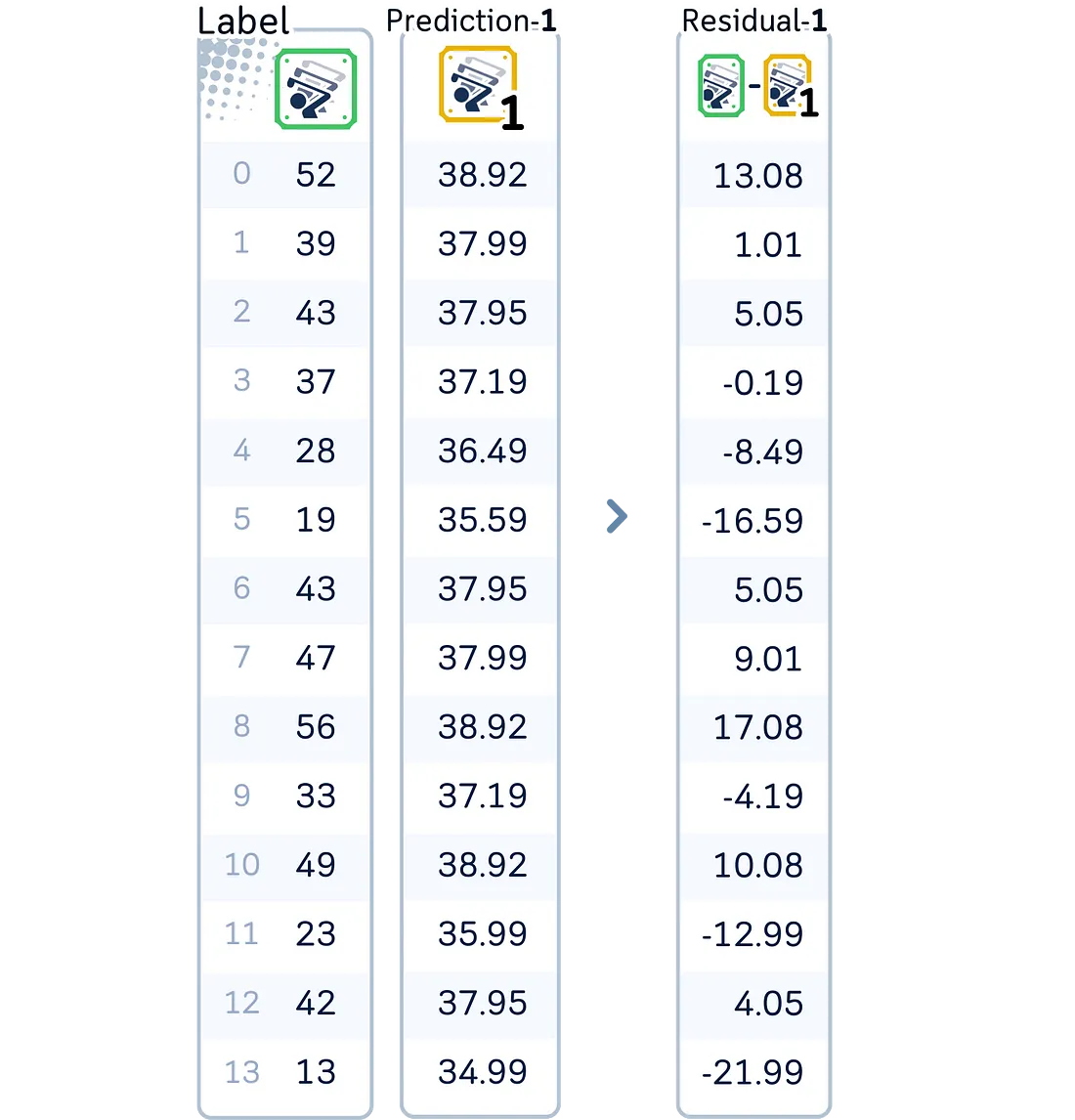
2.1. 基于当前模型计算新的残差

a. 计算目标值与当前预测值之间的差异。

这些残差将与第一次迭代时的残差有所不同。

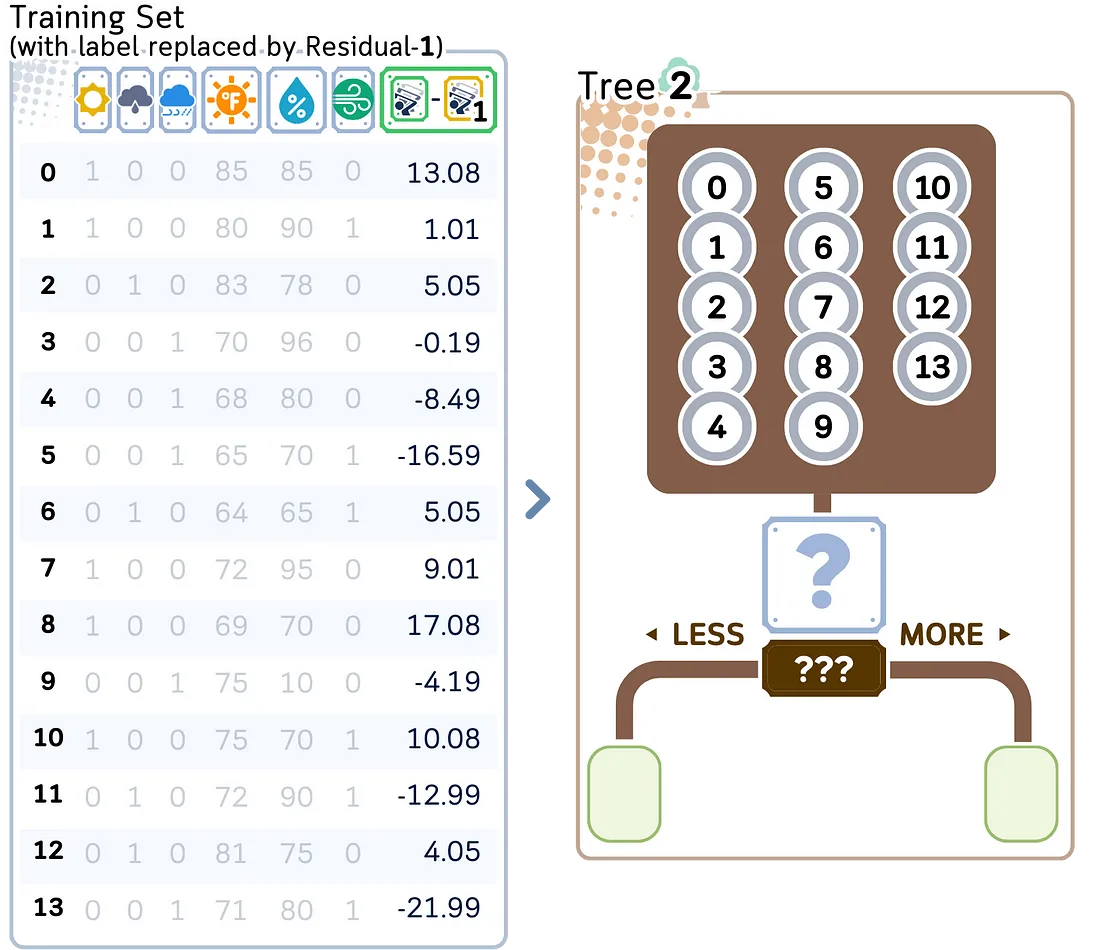
2.2. 构建一棵新树来预测这些残差。过程与第一棵树相同，但目标是新的残差。

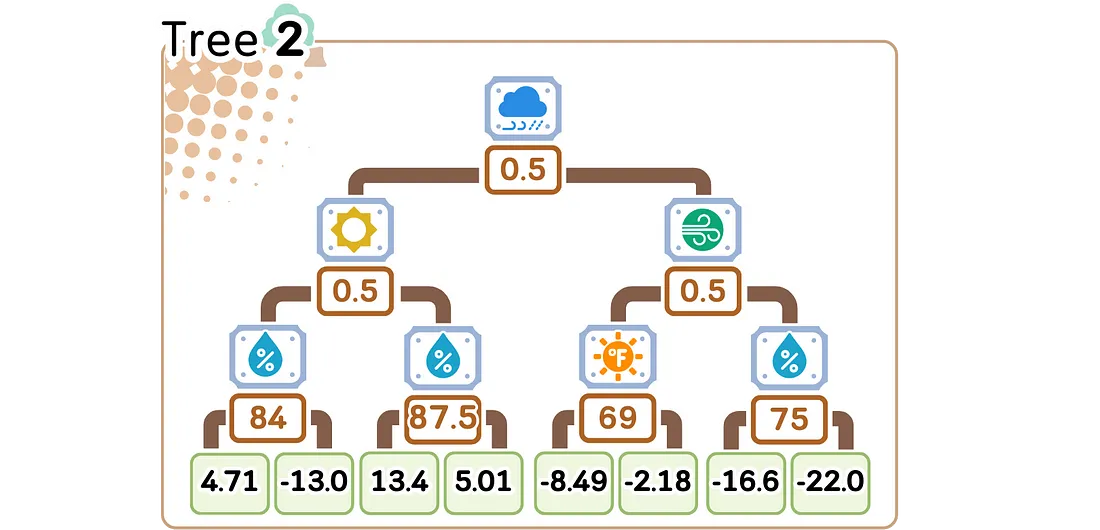
2.3. 计算每个叶节点的平均残差。

2.4. 更新模型预测

· 将新树的预测结果乘以学习率。

· 将新的缩放后的树预测结果累加到当前总和中。

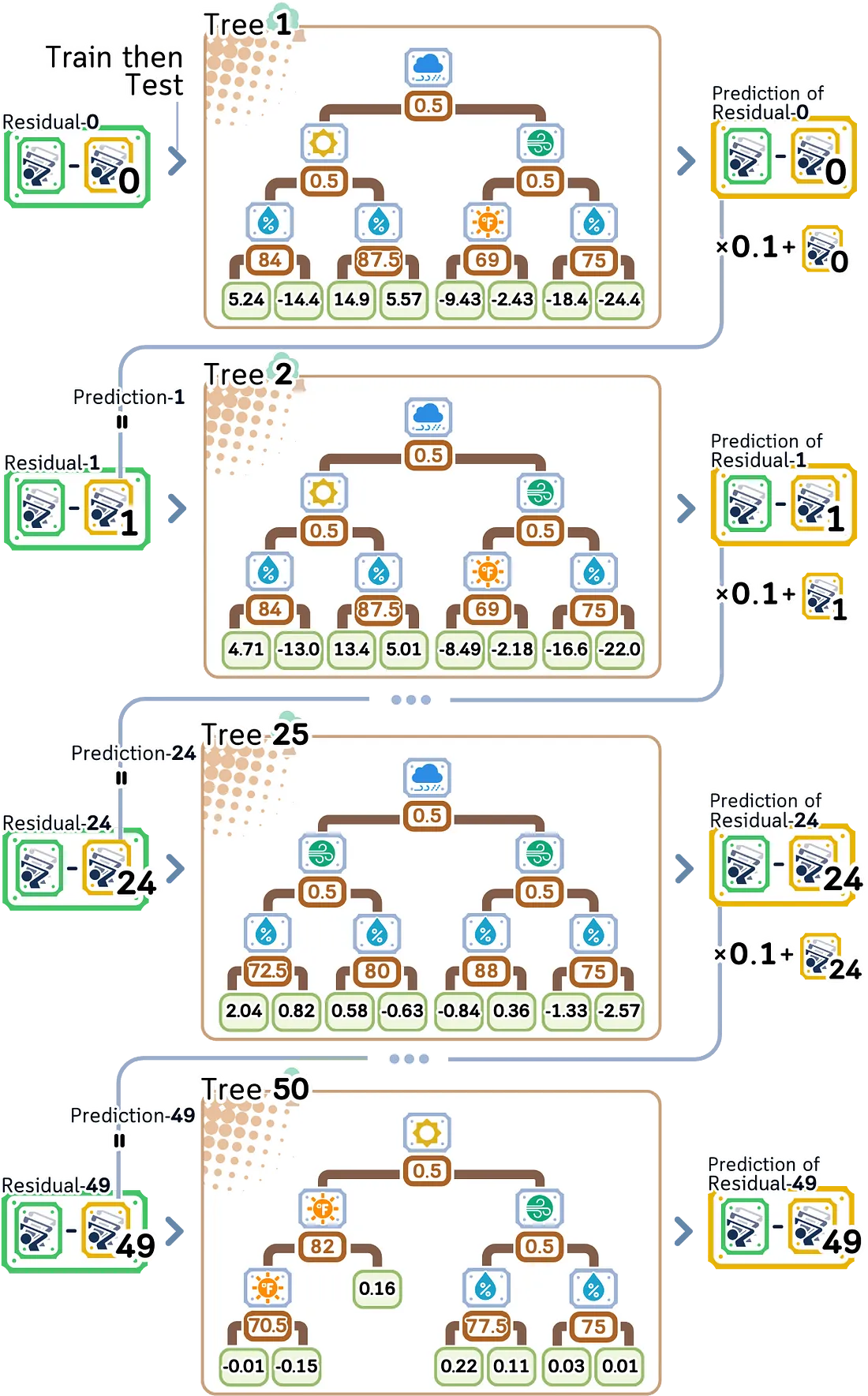
对于第三棵树及之后的树：

重复步骤2.1–2.3，直到完成剩余的迭代。请注意，每棵树都会看到不同的残差。

· 树逐渐关注更难预测的模式

· 学习率通过限制每棵树的贡献来防止过拟合

from sklearn.tree import plot_tree
import matplotlib.pyplot as plt
from sklearn.ensemble import GradientBoostingRegressor
# Train the model
clf = GradientBoostingRegressor(criterion='squared_error', learning_rate=0.1, random_state=42)
clf.fit(X_train, y_train)
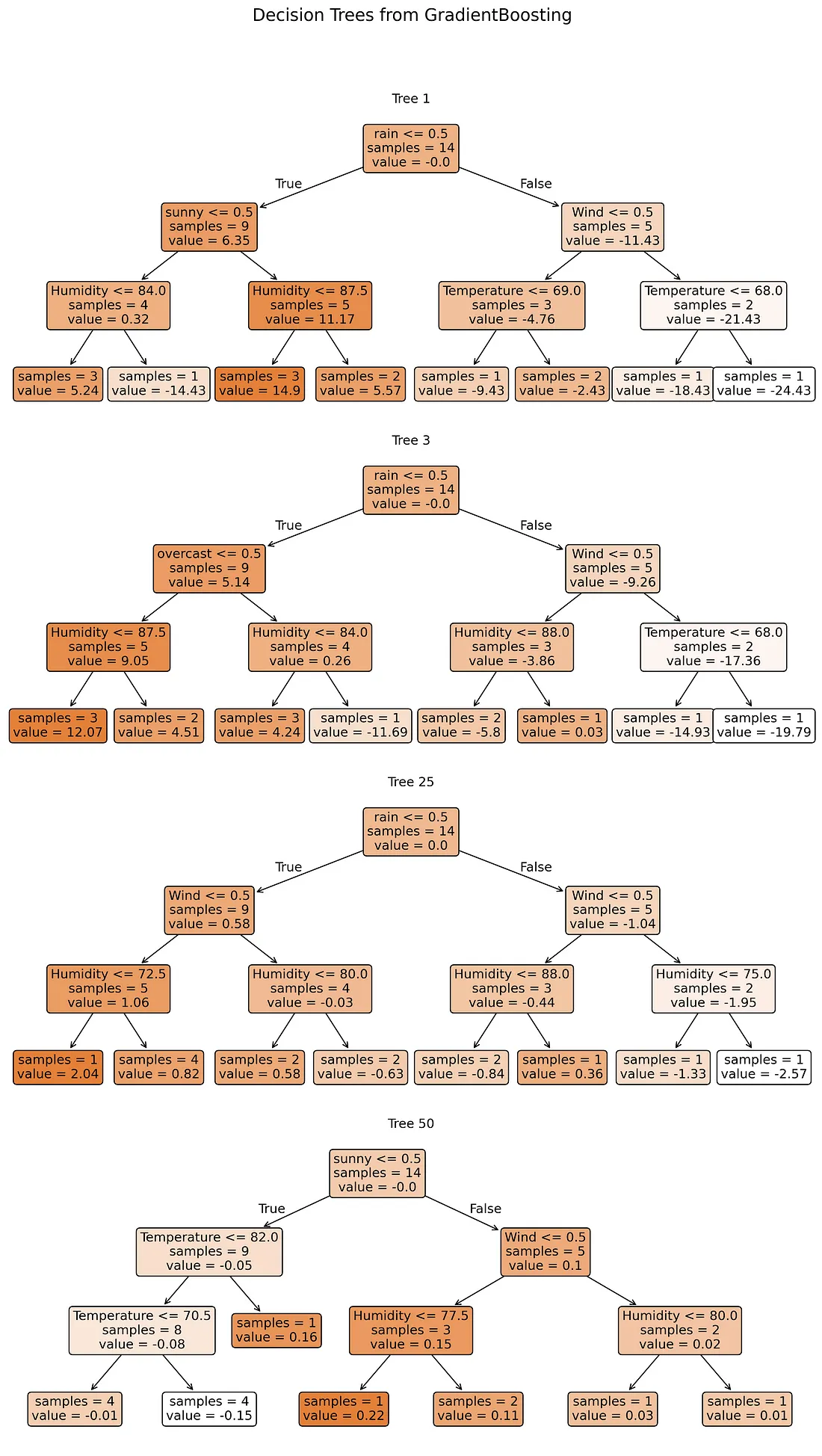
# Plot trees 1, 2, 49, and 50
plt.figure(figsize=(11, 20), dpi=300)
for i, tree_idx in enumerate([0, 2, 24, 49]):
    plt.subplot(4, 1, i+1)
    plot_tree(clf.estimators_[tree_idx,0], 
              feature_names=X_train.columns,
              impurity=False,
              filled=True, 
              rounded=True,
              precision=2,
              fontsize=12)
    plt.title(f'Tree {tree_idx + 1}')
plt.suptitle('Decision Trees from GradientBoosting', fontsize=16)
plt.tight_layout(rect=[0, 0.03, 1, 0.95])
plt.show()

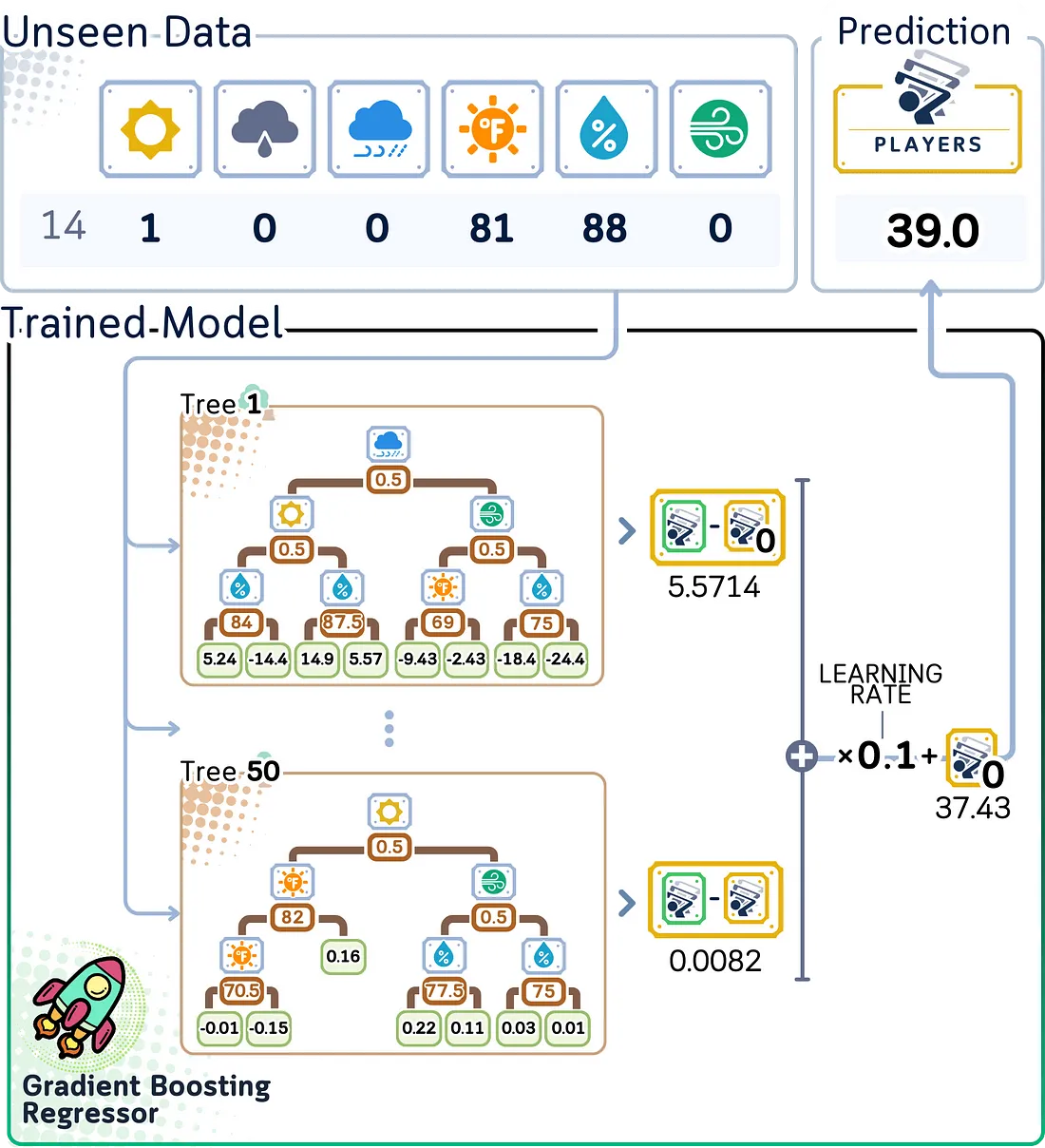
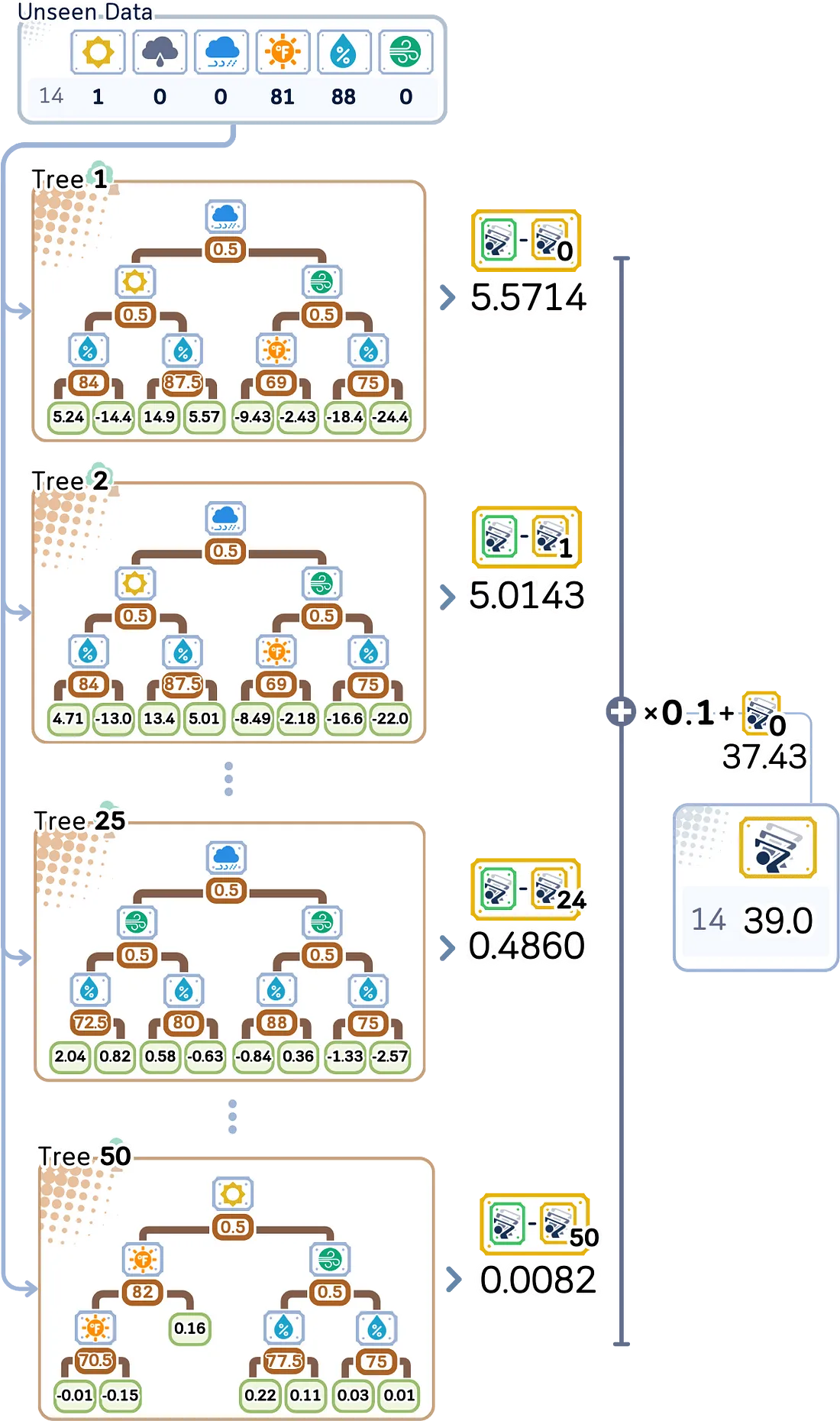
测试步骤

对于预测：

a. 从初始预测（玩家平均数量）开始

b. 将输入数据通过每棵树以获得其预测的调整值

c. 按学习率缩放每棵树的预测结果

d. 将所有这些调整值加到初始预测上

e. 总和直接给出我们预测的玩家数量

评估步骤

在构建完所有树之后，我们可以对测试集进行评估。

# Get predictions
y_pred = clf.predict(X_test)
# Create DataFrame with actual and predicted values
results_df = pd.DataFrame({
    'Actual': y_test,
    'Predicted': y_pred
})
print(results_df) # Display results DataFrame
# Calculate and display RMSE
from sklearn.metrics import root_mean_squared_error
rmse = root_mean_squared_error(y_test, y_pred)
print(f"\nModel Accuracy: {rmse:.4f}")

关键参数

在scikit-learn等库中，梯度提升的关键参数包括：

max_depth：用于建模残差的树的深度。与AdaBoost使用浅树（树桩）不同，梯度提升在树较深时（通常为3-8层）效果更好。更深的树能捕捉更复杂的模式，但存在过拟合的风险。

n_estimators：要使用的树的数量（通常为100-1000棵）。当与学习率较小时，更多的树通常能提高性能。

learning_rate：也称为“收缩率”，用于缩放每棵树的贡献（通常为0.01-0.1）。较小的值需要更多的树，但通过学习过程的细化，往往能获得更好的结果。

subsample：用于训练每棵树的数据样本比例（通常为0.5-0.8）。这个可选功能增加了随机性，可以提高模型的稳健性并减少过拟合。

这些参数相互作用：较小的学习率需要更多的树，而更深的树可能需要较小的学习率来避免过拟合。

与AdaBoost的主要区别

AdaBoost和梯度提升都是提升算法，但它们从错误中学习的方式不同。以下是主要区别：

1. 梯度提升的max_depth通常较高（3-8），而AdaBoost更倾向于使用浅树（树桩）。
2. 梯度提升使用残差而不是样本权重，因此没有sample_weight更新。
3. 梯度提升的learning_rate通常要小得多（0.01-0.1），而AdaBoost的值较大（0.1-1.0）。
4. 梯度提升的初始预测从均值开始，而AdaBoost从0开始。
5. 树通过简单相加而不是加权投票来组合，使得每棵树的贡献更直接。
6. 梯度提升有可选的subsample参数来增加随机性，这是标准AdaBoost所没有的。

优缺点

优点：

• 逐步错误修正：在梯度提升中，每棵新树都专注于纠正之前树所犯的错误。这使得模型在先前出错的地方能够更好地改进预测。
• 灵活的错误度量：与AdaBoost不同，梯度提升可以优化不同类型的错误度量（如平均绝对误差、均方误差等）。这使得它能够适应各种问题。
• 高准确性：通过使用更详细的树和仔细控制学习率，梯度提升通常比其他算法提供更准确的结果，特别是对于结构良好的数据。

缺点：

• 过拟合风险：使用更深的树和顺序构建过程可能导致模型过于紧密地拟合训练数据，从而降低在新数据上的性能。这需要仔细调整树深度、学习率和树的数量。
• 训练过程缓慢：与可以并行构建树的算法（如随机森林）相比，梯度提升必须一棵接一棵地构建树，因此训练速度较慢。每棵树都依赖于之前树的错误。
• 内存使用高：需要更深和更多的树意味着梯度提升可能比更简单的提升方法（如AdaBoost）消耗更多的内存。
• 对设置敏感：梯度提升的有效性在很大程度上取决于找到学习率、树深度和树数量的正确组合，这可能比调整更简单算法更复杂和耗时。

总结

梯度提升是提升算法中的一项重大改进。这种成功催生了像XGBoost和LightGBM这样的流行版本，它们在机器学习竞赛和实际应用中得到了广泛应用。

虽然梯度提升比更简单的算法需要更仔细的调整，特别是在调整决策树的深度、学习率和树的数量时，但它非常灵活且强大。这使得它成为处理结构化数据问题的首选。

梯度提升能够处理简单方法（如AdaBoost）可能忽略的复杂关系。其持续的流行和不断的改进表明，使用梯度和逐步构建模型的方法在现代机器学习中仍然非常重要。

 梯度提升回归器代码总结

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
from sklearn.ensemble import GradientBoostingRegressor
# Create dataset
dataset_dict = {
   'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 
               'sunny', 'sunny', 'rain', 'sunny', 'overcast', 'overcast', 'rain',
               'sunny', 'overcast', 'rain', 'sunny', 'sunny', 'rain', 'overcast',
               'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
   'Temp.': [85.0, 80.0, 83.0, 70.0, 68.0, 65.0, 64.0, 72.0, 69.0, 75.0, 75.0,
             72.0, 81.0, 71.0, 81.0, 74.0, 76.0, 78.0, 82.0, 67.0, 85.0, 73.0,
             88.0, 77.0, 79.0, 80.0, 66.0, 84.0],
   'Humid.': [85.0, 90.0, 78.0, 96.0, 80.0, 70.0, 65.0, 95.0, 70.0, 80.0, 70.0,
              90.0, 75.0, 80.0, 88.0, 92.0, 85.0, 75.0, 92.0, 90.0, 85.0, 88.0,
              65.0, 70.0, 60.0, 95.0, 70.0, 78.0],
   'Wind': [False, True, False, False, False, True, True, False, False, False, True,
            True, False, True, True, False, False, True, False, True, True, False,
            True, False, False, True, False, False],
   'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29,
                   25, 51, 41, 14, 34, 29, 49, 36, 57, 21, 23, 41]
}
# Prepare data
df = pd.DataFrame(dataset_dict)
df = pd.get_dummies(df, columns=['Outlook'], prefix='', prefix_sep='')
df['Wind'] = df['Wind'].astype(int)
# Split features and target
X, y = df.drop('Num_Players', axis=1), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Train Gradient Boosting
gb = GradientBoostingRegressor(
   n_estimators=50,     # Number of boosting stages (trees)
   learning_rate=0.1,    # Shrinks the contribution of each tree
   max_depth=3,          # Depth of each tree
   subsample=0.8,        # Fraction of samples used for each tree
   random_state=42
)
gb.fit(X_train, y_train)
# Predict and evaluate
y_pred = gb.predict(X_test)
rmse = root_mean_squared_error(y_test, y_pred))
print(f"Root Mean Squared Error: {rmse:.2f}")