本文探讨了如何创建一系列较小的异常值检测器，每个检测器处理特征的一个子集（称为子空间），而不是使用单个异常值检测器来检查数据集中的所有特征。

异常值检测的挑战

在对表格数据进行异常值检测时，我们寻找的是数据中最不寻常的记录——这些记录要么相对于同一数据集中的其他记录，要么相对于之前的数据而言。

在寻找最有意义的异常值时，存在许多挑战，特别是没有明确的统计异常定义来指定哪些数据中的异常应被视为最强的。此外，对于你的项目而言最相关的异常值（不一定是统计上最不寻常的）将是特定的，并且可能随时间而变化。

异常值检测中还存在许多技术挑战。其中之一是当数据具有许多特征时出现的困难。如在之前关于计数异常值检测器和共享最近邻的文章中所讨论的，当特征众多时，我们经常会面临一个被称为“维度诅咒”的问题。

这对异常值检测产生了一系列影响，包括使距离度量变得不可靠。许多异常值检测算法依赖于计算记录之间的距离——以便将与其他记录相似度异常低的记录以及与其他记录差异异常大的记录识别为异常值——即与其他记录距离近的记录少，而与其他记录距离远的记录多。

例如，如果我们有一个包含40个特征的表格，那么数据中的每条记录都可以被视为40维空间中的一个点，并且其异常程度可以通过它与此空间中的其他点之间的距离来评估。这要求有一种方法来测量记录之间的距离。使用了多种度量方法，其中欧几里得距离相当常见（假设数据是数值型的，或者已转换为数值型）。因此，每条记录的异常程度通常基于它与数据集中其他记录之间的欧几里得距离来衡量。

然而，当处理许多特征时，这些距离计算可能会失效，实际上，即使只有十个或二十个特征，甚至经常是有三十个、四十个或更多特征时，距离度量的问题也可能出现。

我们应该注意的是，处理大量特征的问题并不是所有异常值检测器都会遇到的。例如，当使用单变量测试（如z分数或四分位数范围测试，这些测试每次只考虑一个特征，独立于其他特征或使用如FPOF这样的分类异常值检测器时，这些问题通常不会很严重。

然而，大多数常用的异常值检测器是数值型多变量异常值检测器——这些检测器假设所有特征都是数值型的，并且通常一次性处理所有特征。例如，LOF（局部异常值因子）和KNN（k-最近邻）是两种使用最广泛的检测器，它们都是基于每个记录与其他记录之间的距离（数据点所在的高维空间中）来评估其异常程度的。

基于与其他数据点距离的异常值示例

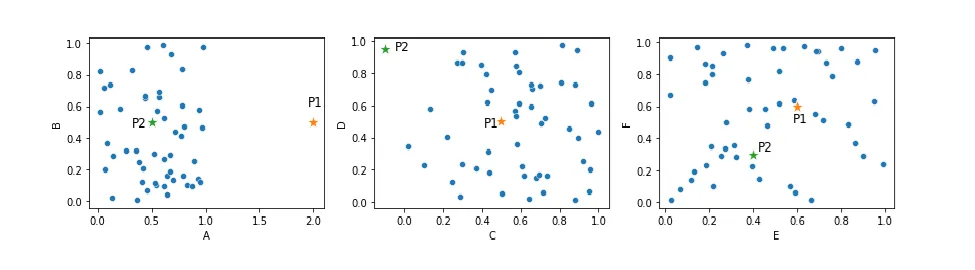
考虑下面的图。这展示了一个包含六个特征的数据集，以三个二维散点图的形式呈现。这包括两个可以合理地被视为异常值的点，P1和P2。

现在来看P1，它在特征A中远离其他点。也就是说，仅考虑特征A，P1可以很容易地被标记为异常值。然而，大多数检测器会使用所有六个维度的距离来考虑每个点与其他点的距离，这不幸的是意味着P1可能不一定会作为异常值脱颖而出，因为高维空间中的距离计算具有其特性。P1在其他五个特征中相当典型，因此它在6维空间中的距离可能相当正常。

尽管如此，我们可以看到这种基于异常值检测的一般方法（即检查每个记录到其他记录的距离）是相当合理的：P1和P2是异常值，因为它们在某些维度上（至少）远离其他点。

KNN和LOF算法

由于KNN（K-最近邻）和LOF（局部离群因子）是非常常用的检测器，我们将在这里更仔细地研究它们，然后特别研究在子空间中使用这些算法的情况。

在KNN离群点检测器中，我们选择一个k值，它决定了每个记录要与多少个邻居进行比较。假设我们选择10（在实践中，这是一个相当典型的值）。

对于每条记录，我们测量它与10个最近邻居的距离，这可以很好地反映每个点的孤立和偏远程度。然后，我们需要基于这10个距离为每个记录创建一个单一的离群得分（即一个数字）。为此，我们通常取这些距离的平均值或最大值。

假设我们取最大值（使用平均值、中位数或其他函数也可以，尽管每种都有其细微差别）。如果一条记录与其第10个最近邻居的距离异常大，这意味着最多只有9条记录与它相当接近（可能更少），而它与大多数其他点的距离都异常远，因此可以被视为离群点。

在LOF离群点检测器中，我们使用了类似但略有不同的方法。我们也查看每个点到其k个最近邻居的距离，但随后将这些距离与这些k个邻居到它们各自k个最近邻居的距离进行比较。因此，LOF根据每个点在其邻域中的其他点来衡量该点的离群程度。

也就是说，KNN使用全局标准来确定哪些距离到邻居的异常大，而LOF则使用局部标准来确定哪些距离是异常大的。

LOF算法的细节实际上更为复杂，这两种算法（以及这些算法的许多变体）之间的具体差异所带来的影响。

这些考虑本身很有趣，但这里的要点是，KNN和LOF都是基于记录与其最近邻居的距离来评估记录的。而且，如果使用许多特征，这些距离度量可能会效果不佳（甚至完全失效），而通过一次只处理少量特征（子空间）可以大大减少这种情况。

即使在使用不基于距离度量的检测器时，使用子空间的想法也是有用的，但在使用类似于KNN和LOF的方式进行距离计算的检测器中，使用子空间的一些好处可能更加明显。例如，除了KNN和LOF之外，Radius、ODIN、INFLO、LoOP检测器，以及基于采样和基于聚类的检测器，都使用距离。

然而，其他问题，如维度诅咒，也可能发生在其他检测器中。例如，ABOD（基于角度的离群检测器）使用记录之间的角度来评估每条记录的离群程度，而不是距离。但是，思路是相似的，使用子空间在使用ABOD时也是有帮助的。

此外，下面我将介绍的使用子空间的其他好处同样适用于许多检测器，无论它们是否使用距离计算。尽管如此，维度诅咒在离群检测中是一个严重的问题：当检测器使用距离计算（或类似的度量，如角度计算）并且存在许多特征时，这些距离计算可能会失效。在上面的图中，考虑到只有六个维度，P1和P2可能会被很好地检测到，并且即使在使用10个或20个特征时也可能如此，但如果存在，比如说，100个维度，那么所有点之间的距离实际上都会变得差不多，P1和P2根本不会显得异常。

中等数量特征带来的问题

除了与处理大量特征相关的问题外，我们尝试在数据集中识别最不寻常的记录时，即使处理相当少量的特征，也可能会受到破坏。

虽然大量的特征可能会使记录之间的距离计算变得毫无意义，但即使中等数量的特征也会使仅在一两个特征上异常的记录更难识别。

再次考虑之前展示的散点图，这里重复展示。点P1在特征A上是离群点（但在其他五个特征上不是）。点P2在特征C和D上异常，但在其他四个特征上不是。然而，当考虑这些点在6维空间中的欧几里得距离时，它们可能不会可靠地突显为离群点。使用曼哈顿距离和大多数其他距离度量也是如此。

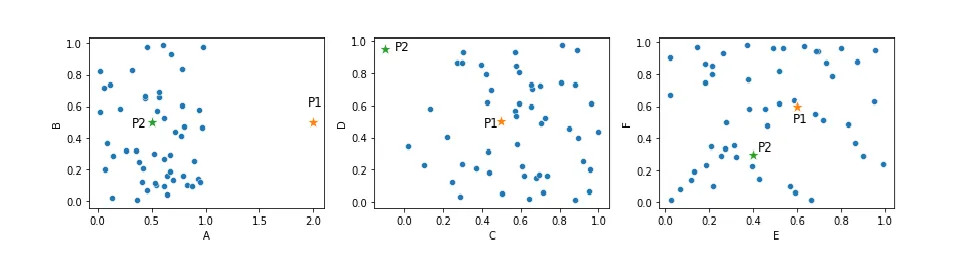
例如，在最左边图中所示的二维空间中，P1 并不比其他大多数点远得异常。异常的是它周围没有其他点（这是 KNN 和 LOF 能够检测到的），但在该二维空间中，P1 到其他点的距离并不异常：它与大多数其他点对之间的距离相似。

使用 KNN 算法，如果我们将 k 设置得相对较低，例如 5 或 10，那么我们很可能能够检测到这一点——大多数记录的第五个（和第十个）最近邻点的距离比 P1 要近得多。然而，当在计算中包含所有六个特征时，这一点就不像仅查看特征 A，或者仅查看最左边的图（仅包含特征 A 和 B）时那么清晰了。

在考虑仅特征 C 和 D 时，P2 作为一个离群点非常突出。使用 k 值为 5 的 KNN 检测器，我们可以找到其 5 个最近邻点，并且到这些点的距离会比数据集中典型点的距离要大。

同样，使用 k 值为 5 的 LOF 检测器，我们可以比较 P1 或 P2 到其 5 个最近邻点的距离与这些最近邻点到它们各自 5 个最近邻点的距离，在这里也会发现，P1 或 P2 到其 5 个最近邻点的距离异常地大。

至少在考虑仅特征 A 和 B，或特征 C 和 D 时，这是直截了当的，但是，当考虑完整的 6 维空间时，它们作为离群点的识别就变得更加困难了。

虽然许多离群点检测器即使在有六个或更多维度的情况下仍然能够识别 P1 和 P2，但使用更少的特征显然更容易也更可靠。为了检测 P1，我们实际上只需要考虑特征 A；为了识别 P2，我们只需要考虑特征 C 和 D。在过程中包含其他特征只会使识别变得更加困难。

这实际上是离群点检测中的一个常见问题。我们处理的数据集中经常包含许多特征，每个特征都可能有用。例如，如果我们有一个包含 50 个特征的表，可能这 50 个特征都是相关的：其中任何一个特征的罕见值都会很有趣，或者这 50 个特征中任意两个或更多特征的罕见值组合都会很有趣。那么，保留所有 50 个特征进行分析就是值得的。

但是，为了识别任何一个异常值，我们通常只需要少数几个特征。事实上，一个记录在所有特征中都出现异常的情况非常罕见。而且，一个记录基于许多特征的罕见值组合而出现异常的情况也非常罕见。

任何给定的离群点很可能在一个或两个特征中具有罕见值，或者在一对或一组（可能是三个或四个）特征中具有罕见值组合。只需这些特征就足以识别该行中的异常值，即使其他特征对于检测其他行中的异常值可能是必要的。

子空间

为了解决上述问题，离群点检测中一个重要的技术是使用子空间。子空间一词简单地指的是特征的子集。在上面的例子中，如果我们使用子空间：A-B、C-D、E-F、A-E、B-C、B-D-F 和 A-B-E，那么我们就有了七个子空间（五个二维子空间和两个三维子空间）。创建这些子空间后，我们会在每个子空间上运行一个（或多个）检测器，因此每个记录上至少会运行七个检测器。

现实情况是，当我们拥有比六个更多的特征时，子空间会变得更加有用，而且一般来说，子空间本身甚至会包含超过六个特征，而不仅仅是两个或三个。但现在，通过观察这个具有少量小子空间的简单案例，我们很容易理解这一点。

使用这些子空间，我们可以更可靠地找到P1和P2作为离群点。运行于特征A-B上的检测器、运行于特征A-E上的检测器以及运行于特征A-B-E上的检测器可能会给P1打出高分。而P2则很可能被运行于特征C-D上的检测器，以及可能还有运行于特征B-C上的检测器所检测到。

然而，我们必须小心：仅使用这七个子空间，而不是覆盖所有特征的单个6维空间，可能会错过某些罕见的特征组合，例如A和D，或C和E。使用覆盖所有六个特征的检测器可能会检测到这些组合，也可能检测不到，但使用一组从未检查过这些特征组合的检测器则肯定无法检测到。

使用子空间确实有很大的好处，但也存在错过相关离群点的风险。我们将在下面介绍一些生成子空间的技术来缓解这个问题，但在整个数据空间上运行一个或多个离群点检测器也是有用的。一般来说，在离群点检测中，除非我们应用多种技术，否则很少能够找到我们感兴趣的全部离群点。尽管使用子空间非常重要，但使用多种技术仍然常常是有用的，这可能包括在整个数据上运行一些检测器。

同样，在每个子空间中，我们可能会执行多个检测器。例如，我们可能会同时使用KNN和LOF检测器，以及Radius、ABOD和可能的其他一些检测器——再次强调，使用多种技术可以让我们更好地覆盖我们希望检测到的离群点范围。

进一步使用子空间的动机

我们已经看到了使用子空间的几个动机：我们可以缓解维度诅咒，并且可以减少因基于少数特征而淹没在众多特征中的异常未被可靠识别的情况。

除了处理这样的情况外，使用子空间进行离群点检测还有许多其他优点。这些优点包括：

• 由于使用集成效应而提高的准确性——使用多个子空间允许我们创建集成（离群点检测器的集合），从而可以组合多个检测器的结果。一般来说，使用检测器集成比使用单个检测器提供更高的准确性。这与（尽管也有一些真正的差异）分类和回归问题中预测器集成往往比单个预测器更强的方式相似。在这里，使用子空间可以让每个记录被多次检查，这为每个记录提供了比任何单个检测器都更稳定的评估。
• 可解释性——结果可以更具可解释性，而可解释性往往是离群点检测中的一个关键问题。在离群点检测中，我们经常标记不寻常的记录，认为它们可能是某种程度上的关注点或问题点，并且这些记录通常会被手动检查。为了高效有效地进行这项工作，必须知道它们为什么是不寻常的。手动评估由检查了许多特征的检测器标记的离群点可能特别困难；另一方面，由仅使用了少数特征的检测器标记的离群点可能更容易管理。
• 更快的系统——使用更少的特征可以让我们创建更快（且内存占用更少）的检测器。这可以加快拟合和推理的速度，特别是在使用执行时间与特征数量呈非线性关系的检测器时（例如，许多检测器的执行时间基于特征数量是二次方的）。根据检测器的不同，使用例如20个每个覆盖8个特征的检测器，实际上可能比使用单个覆盖100个特征的检测器执行得更快。
• 并行执行——鉴于我们使用的是许多小型检测器而不是一个大型检测器，因此可以并行执行拟合和预测步骤，从而在具备硬件资源支持的情况下实现更快的执行。
• 随时间调整的简便性——使用许多简单的检测器可以创建一个随时间更容易调整的系统。在离群点检测中，我们经常只是评估单个数据集并希望识别出其中的离群点。但也很常见的是在长期运行的基础上执行离群点检测系统，例如监测工业过程、网站活动、金融交易、输入到机器学习系统或其他软件应用程序中的数据、这些系统的输出等。在这些情况下，我们通常希望随着时间的推移改进离群点检测系统，以便更好地关注更相关的离群点。拥有一套基于少数特征的简单检测器使得这一管理变得更加容易。它允许我们随着时间的推移增加更有用检测器的权重，并减少较不有用检测器的权重。

选择子空间

如前所述，对于每个评估的数据集，我们需要确定适当的子空间。然而，找到相关的子空间集，或者至少找到最优的子空间集，可能是困难的。也就是说，如果我们想找到任何不寻常的值组合，就很难知道哪些特征集将包含最相关的不寻常组合。

例如，如果一个数据集有100个特征，我们可能会训练10个模型，每个模型覆盖10个特征。我们可以使用前10个特征作为第一个检测器，第二个10个特征作为第二个检测器，以此类推。如果前两个特征中有一些行具有异常的值组合，我们将能够检测到这一点。但是，如果与第一个特征相关的异常组合和未由同一模型覆盖的其他90个特征中的任何一个相关，我们将错过这些组合。

我们可以通过使用更多的子空间来提高将相关特征组合在一起的机会，但很难确保所有应该组合在一起的特征集至少组合在一起一次，特别是在数据中存在基于三个、四个或更多特征的相关异常值时——这些特征必须至少在一个子空间中同时出现才能被检测到。例如，在员工费用表中，你可能希望识别出罕见部门、费用类型和金额组合的费用。如果是这样，这三个特征必须至少在一个子空间中同时出现。

因此，我们面临的问题是：每个子空间中应该有多少特征、哪些特征应该组合在一起以及要创建多少个子空间。

需要考虑的组合数量非常大。如果有20个特征，就有2的20次方个可能的子空间，即超过一百万个。如果有30个特征，就有超过十亿个。如果我们提前决定每个子空间中将有多少特征，那么组合的数量就会减少，但仍然很大。如果有20个特征，我们希望每个子空间有8个特征，那么就有20选8，即125,970种组合。如果有30个特征，我们希望每个子空间有7个特征，那么就有30选7，即2,035,800种组合。

我们可能希望采取的一种方法是保持子空间较小，这样可以提高可解释性。最可解释的选项是每个子空间使用两个特征，这也便于简单可视化。然而，如果我们有d个特征，我们需要d*(d-1)/2个模型来覆盖所有组合，这可能难以实现。对于100个特征，我们需要4,950个检测器。我们通常需要在每个检测器中使用至少几个特征，但不必太多。

我们希望使用足够的检测器和每个检测器中有足够的特征，使得每对特征理想上至少同时出现一次，并且每个检测器中的特征数量足够少，以至于检测器之间的特征有很大差异。例如，如果每个检测器使用90个特征中的100个，我们将很好地覆盖所有特征组合，但子空间仍然会很大（这抵消了使用子空间的大部分好处），并且所有子空间都会非常相似（这抵消了创建集成的大部分好处）。

虽然每个子空间的特征数量需要在这些关注点之间取得平衡，但创建的子空间数量则相对简单一些：从准确性角度来看，使用更多子空间严格来说更好，但计算成本也更高。

有几种广泛的方法来寻找有用的子空间。我在这里简要列出这些方法，然后在下面更详细地讨论其中一些。

• 基于领域知识：我们考虑哪些特征集可能具有我们认为值得注意的值组合。
• 基于关联：不寻常的值组合只有在特征之间存在某种关联时才可能出现。在预测问题中，我们通常希望最小化特征之间的相关性，但在异常检测中，这些是最有用的特征，可以一起考虑。关联最强的特征将具有最有意义的异常值，如果存在正常模式的例外。
• 基于寻找非常稀疏的区域：记录通常被认为是异常值，如果它们与数据中的大多数其他记录不同，这意味着它们位于数据的稀疏区域。因此，有用的子空间可以被发现为那些包含大且几乎为空区域的子空间。
• 随机选择：这是后文所示的一种技术FeatureBagging所使用的方法，虽然它可能不是最优的，但它避免了寻找关联和稀疏区域的昂贵搜索，并且在使用大量子空间时可以相当好地工作。
• 穷举搜索：这是Counts Outlier Detector所采用的方法。它仅限于具有少量特征的子空间，但结果具有高度可解释性。它还避免了与选择仅部分可能子空间相关的任何计算或偏差。
• 使用与已知异常值相关的特征：如果我们有一组已知的异常值，可以确定它们为什么是异常值（相关特征），并且处于我们不希望识别未知异常值（仅识别这些特定异常值）的情况下，那么我们可以利用这一点，识别每个已知异常值的相关特征集，并为所需的各种特征集构建模型。

领域知识

让我们以一个数据集为例，具体来说是一个费用表，如下所示。在检查这个表时，我们或许能够确定我们感兴趣和不感兴趣的异常值类型。账户和金额的不寻常组合，以及部门和账户的不寻常组合，可能是我们感兴趣的；而费用日期和时间则可能不是一个有用的组合。我们可以继续以这种方式创建少数几个子空间，每个子空间可能包含两个、三个或四个特征，这样可以实现非常高效且可解释的异常值检测，标记出最相关的异常值。

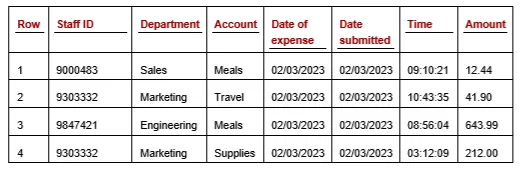
尽管数据中的某些关联可能并不明显，但仅依赖领域知识可能会遗漏这些关联情况。因此，除了利用领域知识外，还值得在数据中搜索关联。我们可以发现特征之间的关系，例如，使用简单的预测模型来测试哪些特征可以准确地从其他特征中预测出来。当我们发现这样的关联时，就值得进一步调查。

然而，发现这些关联虽然对某些目的可能有用，但对于异常值检测过程来说，可能有用也可能没用。例如，如果账户和一天中的时间之间存在关系，这可能仅仅是因为人们通常使用的提交费用的流程导致的，而偏离这种流程的情况可能值得关注，但更可能的是它们并不值得关注。

随机特征子空间

如果没有领域知识可供借鉴，那么随机创建子空间可能是一种有效的方法。这种方法速度快，可以创建一组子空间，这些子空间往往能够捕捉到最显著的异常值，尽管它也可能遗漏一些重要的异常值。

下面的代码提供了一个创建一组随机子空间的方法示例。这个示例使用了一组名为A到H的八个特征，并创建了这些特征的一组子空间。

每个子空间的创建都是从选择到目前为止使用最少的特征开始的（如果有多个特征使用次数相同，则随机选择一个）。它使用一个名为ft_used_counts的变量来跟踪这一点。然后，它一次向这个子空间中添加一个特征，每一步都选择在与子空间中到目前为止已选择的特征一起出现在其他子空间中的次数最少的特征。它使用一个名为ft_pair_mtx的特征来跟踪每对特征到目前为止一起出现在多少个子空间中。通过这样做，我们创建了一组子空间，其中每对特征被匹配到的次数大致相等。

import pandas as pd
import numpy as np
def get_random_subspaces(features_arr, num_base_detectors,
                         num_feats_per_detector):
    num_feats = len(features_arr)
    feat_sets_arr = []
    ft_used_counts = np.zeros(num_feats) 
    ft_pair_mtx = np.zeros((num_feats, num_feats))  
    # Each loop generates one subspace, which is one set of features
    for _ in range(num_base_detectors):  
        # Get the set of features with the minimum count      
        min_count = ft_used_counts.min() 
        idxs = np.where(ft_used_counts == min_count)[0]    
        # Pick one of these randomly and add to the current set
        feat_set = [np.random.choice(idxs)]   
        # Find the remaining set of features
        while len(feat_set) < num_feats_per_detector: 
            mtx_with_set = ft_pair_mtx[:, feat_set]
            sums = mtx_with_set.sum(axis=1)
            min_sum = sums.min()
            min_idxs = np.where(sums==min_sum)[0]
            new_feat = np.random.choice(min_idxs)
            feat_set.append(new_feat)
            feat_set = list(set(feat_set))
            
            # Updates ft_pair_mtx
            for c in feat_set: 
                ft_pair_mtx[c][new_feat] += 1
                ft_pair_mtx[new_feat][c] += 1
            
        # Updates ft_used_counts
        for c in feat_set: 
            ft_used_counts[c] += 1
        feat_sets_arr.append(feat_set)
    return feat_sets_arr
np.random.seed(0)
features_arr = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H'] 
num_base_detectors = 4
num_feats_per_detector = 5
feat_sets_arr = get_random_subspaces(features_arr, 
                                     num_base_detectors, 
                                     num_feats_per_detector)
for feat_set in
    print([features_arr[x] for x in feat_set])

通常情况下，我们会创建比本例中更多的基础检测器（每个子空间通常对应一个基础检测器，但我们也可以在每个子空间上运行多个基础检测器），但为了简单起见，这里只使用了四个。这将输出以下子空间：

['A', 'E', 'F', 'G', 'H']
['B', 'C', 'D', 'F', 'H']
['A', 'B', 'C', 'D', 'E']
['B', 'D', 'E', 'F', 'G']

在创建子空间时，使所有子空间具有相同数量的特征有几个好处，但让子空间涵盖不同数量的特征也有其优势，因为这样可以引入更多的多样性（在创建集成模型时很重要）。不过，无论如何，使用不同的特征本身就能带来很强的多样性（只要每个子空间使用的特征数量相对较少，使得子空间主要由不同的特征构成）。

具有相同数量的特征有几个好处。首先，它简化了模型的调优过程，因为许多异常检测器使用的参数都取决于特征的数量。如果所有子空间具有相同数量的特征，那么它们就可以使用相同的参数。

其次，它简化了分数的组合，因为检测器之间将更具可比性。如果使用不同数量的特征，这可能会产生不同尺度的分数，从而难以比较。例如，在使用k-最近邻（KNN）算法时，如果特征更多，我们预期邻居之间的距离会更大。

基于相关性的特征子空间

在创建子空间时，如果其他条件都相同，那么将相关联的特征尽可能多地放在一起是很有用的。在下面的代码中，我们提供了一个基于相关性选择子空间的代码示例。

测试关联性的方法有很多种。我们可以创建预测模型来尝试从每个单独的特征预测其他特征（这将捕捉到特征之间甚至相对复杂的关系）。对于数值特征，最简单的方法可能是检查斯皮尔曼相关性，虽然这会错过非单调关系，但可以检测到大多数强关系。下面的代码示例中使用的就是这种方法。

要执行代码，我们首先指定所需的子空间数量和每个子空间中的特征数量。

代码的执行过程首先是找到特征之间的所有成对相关性，并将其存储在一个矩阵中。然后，我们创建第一个子空间，从在相关性矩阵中找到最大的相关性开始（这将向此子空间中添加两个特征），然后循环遍历要添加到此子空间中的其他特征数量。对于每个要添加的特征，我们在相关性矩阵中找到最大的相关性，其中一个特征当前在子空间中，而另一个不在。一旦这个子空间具有足够数量的特征，我们就创建下一个子空间，取相关性矩阵中剩余的最大相关性，以此类推。

在这个例子中，我们使用了一个真实的数据集，即来自OpenML的棒球数据集（可通过公共许可证获得）。数据集显示包含一些大的相关性。例如，击球次数和得分之间的相关性为0.94，这表明任何显著偏离这种模式的值都可能是异常值。

import pandas as pd
import numpy as np
from sklearn.datasets import fetch_openml
# Function to find the pair of features remaining in the matrix with the 
# highest correlation
def get_highest_corr(): 
    return np.unravel_index(
        np.argmax(corr_matrix.values, axis=None), 
        corr_matrix.shape)
def get_correlated_subspaces(corr_matrix, num_base_detectors, 
                                num_feats_per_detector):
    sets = []
    # Loop through each subspace to be created
    for _ in range(num_base_detectors): 
        m1, m2 = get_highest_corr()
        # Start each subspace as the two remaining features with 
        # the highest correlation
        curr_set = [m1, m2] 
        for _ in range(2, num_feats_per_detector):
            # Get the other remaining correlations
            m = np.unravel_index(np.argsort(corr_matrix.values, axis=None), 
                                 corr_matrix.shape) 
            m0 = m[0][::-1]
            m1 = m[1][::-1]
            for i in range(len(m0)):
                d0 = m0[i]
                d1 = m1[i]
                # Add the pair if either feature is already in the subset
                if (d0 in curr_set) or (d1 in curr_set): 
                    curr_set.append(d0)
                    curr_set = list(set(curr_set))
                    if len(curr_set) < num_feats_per_detector:
                        curr_set.append(d1)
                        # Remove duplicates
                        curr_set = list(set(curr_set)) 
                if len(curr_set) >= num_feats_per_detector:
                    break
            # Update the correlation matrix, removing the features now used 
            # in the current subspace
            for i in curr_set: 
                i_idx = corr_matrix.index[i]
                for j 
                    j_idx = corr_matrix.columns[j]
                    corr_matrix.loc[i_idx, j_idx] = 0
            if len(curr_set) >= num_feats_per_detector:
                break
        sets.append(curr_set)
    return sets
data = fetch_openml('baseball', version=1)
df = pd.DataFrame(data.data, columns=data.feature_names)
corr_matrix = abs(df.corr(method='spearman'))
corr_matrix = corr_matrix.where(
    np.triu(np.ones(corr_matrix.shape), k=1).astype(np.bool))
corr_matrix = corr_matrix.fillna(0)
feat_sets_arr = get_correlated_subspaces(corr_matrix, num_base_detectors=5, 
                                         num_feats_per_detector=4)
for feat_set in feat_sets_arr:    
    print([df.columns[x] for x in feat_set])

得出的结果：

['Games_played', 'At_bats', 'Runs', 'Hits']
['RBIs', 'At_bats', 'Hits', 'Doubles']
['RBIs', 'Games_played', 'Runs', 'Doubles']
['Walks', 'Runs', 'Games_played', 'Triples']
['RBIs', 'Strikeouts', 'Slugging_pct', 'Home_runs']

PyOD

PyOD可能是当前Python中用于数值表格数据异常检测的最全面且最常用的工具。它包含大量的检测器，从非常简单到非常复杂——包括几种基于深度学习的方法。

现在我们已经了解了子空间在异常检测中的工作原理，接下来我们将查看PyOD提供的两个与子空间一起工作的工具：SOD和FeatureBagging。这两个工具都会识别一组子空间，在每个子空间上执行一个检测器，并将结果组合起来，为每个记录生成一个单一的分数。

无论是否使用子空间，都需要确定使用哪些基础检测器。如果不使用子空间，我们会选择一个或多个检测器，并在完整的数据集上运行它们。而如果我们使用子空间，我们同样会选择一个或多个检测器，但这里是在每个子空间上运行它们。如上所述，LOF和KNN是合理的选择，但PyOD还提供了许多其他检测器，如果在每个子空间上执行，它们也能很好地工作，例如基于角度的异常检测器（ABOD）、基于高斯混合模型（GMM）的模型、核密度估计（KDE）以及其他几种。此外，PyOD之外提供的其他检测器也能非常有效地工作。

SOD（子空间异常检测）

SOD是专门为处理类似上述散点图所示的情况而设计的。SOD的工作原理与KNN和LOF类似，也是通过为每个点识别一个由k个邻居组成的邻域，这个邻域被称为参考集。不过，参考集的查找方式有所不同，它使用了一种称为共享最近邻（SNN）的方法。

这篇文章详细描述了共享最近邻的概念，但大致的想法是，如果两个点是由相同的机制生成的，它们不仅会倾向于彼此靠近，而且还会倾向于有许多相同的邻居。因此，任何两个记录的相似性可以通过它们共有的邻居数量来衡量。鉴于此，邻域的识别不仅可以通过使用欧几里得距离最小的点集（如KNN和LOF所做的那样），还可以通过使用共享邻居最多的点来进行。这种方法即使在高维度和存在许多无关特征的情况下也往往具有鲁棒性：在这些情况下，邻居的排名顺序仍然有意义，因此即使无法确定具体的距离，也可以可靠地找到最近邻居的集合。

一旦我们有了参考集，就可以用它来确定子空间，这里子空间是指能够解释参考集中最大方差的特征集。一旦我们识别出这些子空间，SOD就会检查每个点到数据中心的距离。

下面我提供了一个使用SOD的快速示例。这假设已经安装了pyod，安装命令为：

pip install pyod

我们将使用一个合成数据集作为示例，这样我们就可以对数据与模型超参数进行实验，以更好地了解每个检测器的优势和局限性。这里的代码提供了一个处理35个特征的示例，其中两个特征（第8个和第9个特征）是相关的，而其他特征则是不相关的。通过这两个相关特征的不寻常组合，创建了一个单一的异常值。

SOD能够识别出这个已知的异常值作为首要异常值。我将污染率设置为0.01，以指定（在100条记录的情况下）仅返回一个异常值。然而，在超过35个特征的情况下进行测试时，SOD对这个点的评分要低得多。此示例中将参考集的大小指定为3；使用不同的值可能会看到不同的结果。

import pandas as pd
import numpy as np
from pyod.models.sod import SOD
np.random.seed(0)
d = np.random.randn(100, 35)
d = pd.DataFrame(d)
#A Ensure features 8 and 9 are correlated, while all others are irrelevant
d[9] = d[9] + d[8] 
# Insert a single outlier
d.loc[99, 8] = 3.5 
d.loc[99, 9] = -3.8
#C Execute SOD, flagging only 1 outlier
clf = SOD(ref_set=3, contamination=0.01) 
d['SOD Scores'] = clf.fit (d)
d['SOD Scores'] = clf.labels_

我们在下面展示了四个散点图，分别显示了35个特征中的四对特征。已知的异常值在每个图中都以星号表示。我们可以在第二个窗格中看到特征8和特征9（这两个是相关特征），并且我们可以看到这个点是一个明显的异常值，尽管它在所有其他维度上都是典型的。

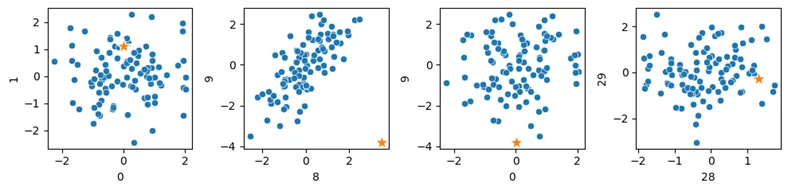
FeatureBagging

FeatureBagging旨在解决与SOD相同的问题，但在确定子空间时采用了不同的方法。它完全随机地创建子空间（与上述示例略有不同，上述示例会记录每对特征被一起放入子空间的频率，并尝试平衡这一点）。它还为每个基础检测器对行进行子采样，从而在检测器之间提供了更多的多样性。

使用指定数量的基础检测器（默认10个，但建议使用更多），每个检测器随机选择一组行和特征。对于每个检测器，可以选择的最大特征数作为参数指定，默认值为全部特征。因此，对于每个基础检测器，FeatureBagging执行以下步骤：

• 确定要使用的特征数量，最多不超过指定的最大值。
• 随机选择这么多特征。
• 随机选择一组行。这是一个与行数相同大小的自助样本。
• 创建一个LOF检测器（默认情况下；也可以使用其他基础检测器）来评估子空间。

完成这些步骤后，每个行将由每个基础检测器进行评分，然后必须将这些评分组合成每个行的单个最终评分。PyOD的FeatureBagging为此提供了两个选项：使用最大评分和使用平均评分。

正如我们在上面的散点图中看到的，点在某些子空间中可能是强异常值，而在其他子空间中则不是，并且在它们典型的子空间中的评分进行平均可能会降低它们的评分，从而抵消使用子空间的好处。在其他形式的异常检测集成中，使用平均值可能效果很好，但在处理多个子空间时，使用最大值通常是两个选项中的较优者。这样做，我们根据每个记录在最不寻常的子空间中的表现来为其评分。这也不是完美的，可能有更好的选项，但使用最大值简单且几乎总是优于使用平均值。

任何检测器都可以在子空间内使用。PyOD默认使用LOF，就像描述FeatureBagging的原始论文一样。LOF是一个强大的检测器，也是一个明智的选择，尽管你可能会发现使用其他基础检测器会获得更好的结果。

在原始论文中，子空间是随机创建的，每个子空间使用d/2到d-1个特征，其中d是特征的总数。一些研究人员指出，原始论文中使用的特征数量可能远大于适当的数量。

如果特征总数很大，一次使用超过一半的特征将会导致维度诅咒生效。并且，在每个检测器中使用许多特征将导致检测器之间相互关联（例如，如果所有基础检测器都使用90%的特征，它们将使用大致相同的特征，并且倾向于对每个记录进行大致相同的评分），这也会消除创建集成的大部分好处。

PyOD允许设置每个子空间中使用的特征数量，并且通常应该设置得相当低，同时创建大量的基础估计器。

使用其他检测器

在本文中，我们探讨了子空间作为提高异常检测性能的多种方式，包括减少维度诅咒、提高可解释性、允许并行执行、允许随时间更容易调整等。这些都是重要的考虑因素，使用子空间通常非常有帮助。

然而，通常还有其他方法也可以用于这些目的，有时作为替代方法，有时与使用子空间相结合。例如，为了提高可解释性，重要的是尽可能选择固有可解释性的模型类型（例如z分数测试、计数异常检测器或PyOD提供的ECOD检测器等单变量测试）。

当主要兴趣在于减少维度诅咒时，同样有用的是查看能够很好地扩展到许多特征的模型类型，例如隔离森林或计数异常检测器。执行单变量测试或应用PCA也可能很有用。

正在进行的异常检测项目

在构建子空间时需要注意的一点是，如果它们是基于相关性或稀疏区域形成的，那么随着数据的变化，相关的子空间可能会随时间而变化。特征之间可能会出现新的关联，并且可能会形成新的稀疏区域，这些对于识别异常值很有用，但如果子空间不时重新计算，这些将被遗漏。以这种方式找到相关的子空间可能非常有效，但它们可能需要根据某种时间表进行更新，或者在已知数据发生变化时进行更新。

结论

在表格数据的异常检测项目中，考虑使用子空间是很常见的，特别是在我们拥有许多特征的情况下。使用子空间是一种相对直接的技术，具有许多值得注意的优势。

当你面临与大数据量、执行时间或内存限制相关的问题时，使用PCA也可能是一种有用的技术，并且在某些情况下可能比创建子空间效果更好。然而，与子空间（以及因此与原始特征，而不是PCA创建的组件）一起工作可能更具可解释性，而在异常检测中，可解释性通常非常重要。

子空间可以与其他技术结合使用，以改进异常值检测。例如，子空间可以与其他方法结合使用来创建集成：可以使用两个子空间（集成中的不同检测器使用不同的特征）以及不同的模型类型、不同的训练行、不同的预处理等来创建更大的集成。这可以提供一些进一步的好处，尽管计算量也会有所增加。