想象一下，你正在处理一个庞大的数据集，并希望训练一个机器学习算法。挑战在于，从海量的变量中决定哪些特征应该被考虑进来，以构建一个有效的模型。这就是特征选择发挥作用的地方，它允许我们筛选掉数据中的冗余，创建出更具解释性和稳健性的模型。

特征选择是从数据集中选择一组特征来训练机器学习算法的过程。特征选择的目的是减少特征的数量，从而提高模型的可解释性和鲁棒性。

特征选择方法可以分为三类：过滤方法、包装方法和嵌入方法。

特征选择方法

过滤方法是与模型无关的特征选择技术，它们基于数据的特性来选择特征，与机器学习模型无关。这类方法的计算成本最低，包括卡方检验、皮尔逊相关系数等。

包装方法是围绕预测模型进行搜索的特征选择算法。它们生成多个特征子集，对每个子集（迭代）训练一个分类或回归模型，并确定其性能。包装方法的计算成本最高。包装方法的例子包括前向选择、后向消除和穷举搜索。

嵌入方法将选择过程“嵌入”到预测模型的训练中。寻找最优特征子集的过程被内置到分类器或回归算法的训练中。因此，嵌入方法只训练一个机器学习模型来选择特征。它们的计算成本等于模型训练时间。

在这篇文章中，我们将重点关注嵌入方法。

嵌入方法

嵌入方法将特征选择“嵌入”到模型构建阶段中。一个典型的嵌入特征选择工作流程包括：

• 训练一个机器学习模型。
• 推导特征重要性。
• 选择排名靠前的预测变量。

最常见的嵌入策略是在线性模型中使用Lasso正则化，以及在决策树中通过信息增益获得特征重要性。

然而，需要注意的是，并非所有机器学习模型都能自然地嵌入特征选择过程。例如，支持向量机（SVM）就不能这样做。

Lasso

线性回归模型基于特征空间的线性组合来预测结果。系数是通过最小化目标值的真实值与预测值之间的平方差来确定的。

主要有三种正则化方法：Ridge正则化、Lasso正则化以及结合了前两者的弹性网络（Elastic Net）。

在Lasso回归中，系数会被一个给定的常数缩小。而在Ridge回归中，系数的平方会被一个常数惩罚。缩小系数的目的是减少偏差并防止过拟合。最佳常数需要通过超参数优化来估计。

事实证明，Lasso正则化有能力将一些系数设置为零。然后，我们可以安全地从数据中移除这些特征。

在下图中，我们看到了随着正则化惩罚的增加，系数的变化。随着惩罚的增加，越来越多的系数被设置为零。

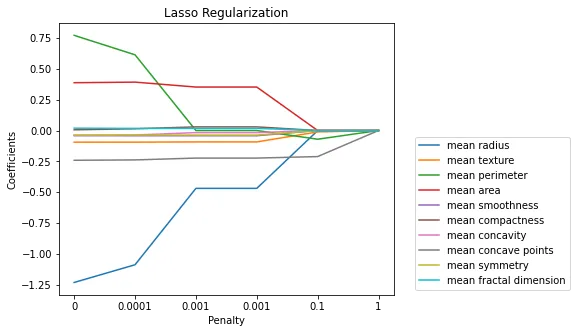
相比之下，Ridge正则化并不具备这种特性，或者至少在惩罚非常大之前不会，如下图所示：

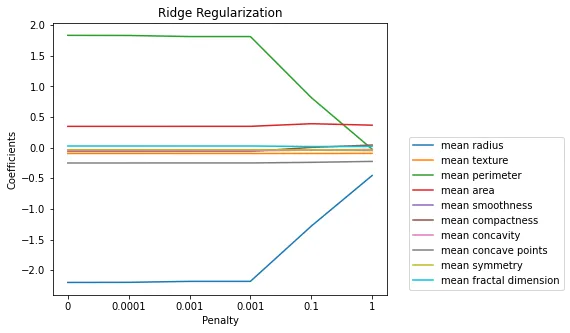
更强的正则化会导致更大的维度降低。

在Python中实现Lasso

让我们来看看如何在Python中使用Lasso来选择相关特征。首先，我们需要导入库、函数和类：

import numpy as np
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import Lasso, LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

让我们从Scikit-learn中导入乳腺癌数据集，并将其拆分为训练集和测试集：

breast_cancer = load_breast_cancer()
X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)
y = breast_cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

让我们设置一个缩放器来标准化特征：

scaler = StandardScaler()
scaler.fit(X_train)

接下来，我们将使用带有Lasso正则化的逻辑回归来选择特征：

sel_ = SelectFromModel(
    LogisticRegression(
        C=0.5, penalty='l1', solver='liblinear', random_state=10),
    )
sel_.fit(scaler.transform(X_train), y_train)

通过执行 sel_.get_support()，我们获得了一个布尔向量，其中非零系数对应的特征位置为 True：

array([False, True, False, False, False, False, False, True, True,
False, True, False, False, False, False, True, False, False,
False, True, True, True, True, True, True, False, True,
True, True, False])

我们可以这样识别被移除特征的名称：

removed_feats = X_train.columns[(sel_.estimator_.coef_ == 0).ravel().tolist()]

如果我们执行 removed_feats，我们将获得以下数组，其中包含将被移除的特征：

Index(['mean radius', 'mean perimeter', 'mean area', 'mean smoothness',
'mean compactness', 'mean concavity', 'mean fractal dimension',
'texture error', 'perimeter error', 'area error', 'smoothness error',
'concavity error', 'concave points error', 'symmetry error',
'worst compactness', 'worst fractal dimension'],
dtype='object')

我们可以这样从训练集和测试集中移除特征：

X_train_selected = sel_.transform(scaler.transform(X_train))
X_test_selected = sel_.transform(scaler.transform(X_test))

如果我们现在执行：

X_train_selected.shape, X_test_selected.shape

我们将获得简化后的数据集的形状：

((426, 14), (143, 14))

决策树中的特征重要性

决策树算法通过顺序划分数据来预测结果。在每个节点上，选择一个特征和一个值来进行划分。最好的划分是使不纯度降低最大化的划分。

有不同的指标可以用来确定“不纯度”。在分类中，算法最小化基尼系数或熵。在回归中，算法最小化均方误差（如最小二乘法）、平均绝对误差或泊松偏差。

每个特征的重要性由整个树中不纯度的总降低量给出。例如，如果一个特征在节点1被用来划分数据，然后又在节点3被使用，那么该特征的重要性由这两个节点不纯度降低的总和来确定。

随机森林并行地生长许多分类树，预测是各棵树预测的平均值。因此，特征重要性是由各棵树平均重要性给出的。

梯度提升机，如xgboost，则构建顺序树，以最小化树的预测与前一棵树残差之间的差异。在这里，特征重要性是各棵树重要性之和。

然后我们可以选择最重要的特征。

Python实现

让我们从基于决策树的模型中选择最重要的特征。我们将使用随机森林和乳腺癌数据集。

首先，让我们导入库、函数和类：

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.datasets import load_breast_cancer
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import train_test_split

让我们加载数据集并将其拆分为训练集和测试集：

breast_cancer = load_breast_cancer()
X = pd.DataFrame(breast_cancer.data, columns=breast_cancer.feature_names)
y = breast_cancer.target
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=0)

让我们基于随机森林分类器得出的特征重要性来选择特征：

sel_ = SelectFromModel(RandomForestClassifier(n_estimators=10, random_state=10))
sel_.fit(X_train, y_train)

SelectFromModel 会选择那些重要性高于所有特征平均重要性的特征。这可以通过参数 threshold 来进行修改。

通过 sel_.get_support()，我们获得了一个布尔向量，其中被选中的特征对应的位置为 True。

array([ True, False, False, True, False, False, True, True, False,
False, True, False, False, False, False, False, False, False,
False, False, False, False, True, True, False, False, False,
True, False, False])

我们可以如下制作一个包含所选特征的列表：

selected_feat = X_train.columns[(sel_.get_support())]

执行 len(selected_feat) 后，我们得到所选特征的数量：8。执行 selected_feat 后，我们得到所选变量的名称：

Index(['mean radius', 'mean area', 'mean concavity', 'mean concave points',
'radius error', 'worst perimeter', 'worst area',
'worst concave points'],
dtype='object')

让我们绘制特征重要性图：

pd.Series(
    sel_.estimator_.feature_importances_.ravel(),
    index=X_train.columns).plot.bar(figsize=(10,5),
)
plt.ylabel('Feature importance')
plt.show()

下面我们看到的是随机森林为每个特征分配的重要性：

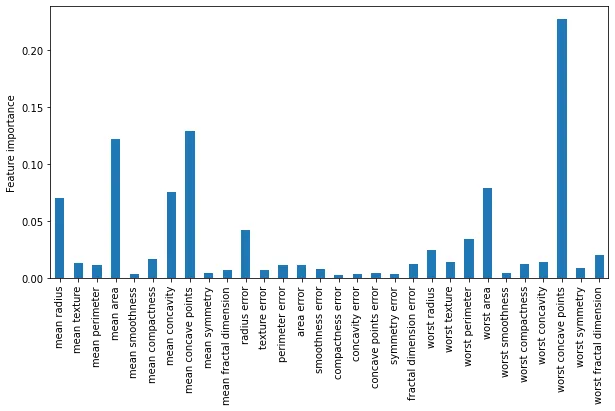
最后，我们可以将数据集缩减到所选变量：

X_train_selected = sel_.transform(X_train)
X_test_selected = sel_.transform(X_test)

就这样，我们现在已经基于决策树获得的重要性选择了特征。

嵌入方法与递归特征消除

从线性回归或决策树中得出的重要性会受到相关性的影响。共线性通常会降低特征的重要性值。因此，为了避免移除那些可能比其他与任何特征都不相关的特征更重要的相关特征，我们倾向于将嵌入方法与递归特征消除相结合。

在递归特征消除中，我们在移除一个或多个不相关特征后重新训练模型。因此，如果一个相关特征被移除，剩余的相关特征将显示出增加的重要性。

import pandas as pd
from sklearn.ensemble import RandomForestClassifier
from sklearn.feature_selection import RFE
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import LabelEncoder
# Load iris dataset
url = "https://gist.githubusercontent.com/curran/a08a1080b88344b0c8a7/raw/0e7a9b0a5d22642a06d3d5b9bcbad9890c8ee534/iris.csv"
df = pd.read_csv(url)
# Separate features and target variable
X = df.drop("species", axis=1)
y = df["species"]
# Initialize RandomForestClassifier
model = RandomForestClassifier()
# Initialize RFE
rfe = RFE(estimator=model, n_features_to_select=1)
# Fit RFE
rfe.fit(X, y)
# Print the ranking
ranking = rfe.ranking_
print("Feature ranking:")
for i, feature in enumerate(X.columns):
    print(f"{feature}: {ranking[i]}")

输出：

Feature ranking:
sepal_length: 3
sepal_width: 4
petal_length: 2
petal_width: 1

结论

总之，嵌入方法为特征选择提供了一种强大且高效的方法，将选择过程无缝集成到模型训练本身中。这不仅与包装方法相比降低了计算复杂度，而且确保了特征选择与模型的预测能力内在一致。对于线性模型的Lasso正则化和基于树的方法中的特征重要性等技术，使我们能够识别并仅保留最相关的特征，从而提高模型性能和可解释性。

然而，必须考虑潜在的陷阱，如共线性，它可能会掩盖某些特征的重要性。将嵌入方法与递归特征消除相结合可以缓解这个问题，提供一个更全面的特征选择过程。通过采用这些方法，你可以在保持特征空间简洁的同时，构建更高效、可扩展和准确的机器学习模型。