蒙特卡洛树搜索 (MCTS) 是一种强大的算法，彻底改变了复杂环境中的决策。它的多功能性使其适用于从游戏到强化学习的各种任务。这篇文章是我对 MCTS 的笔记，涵盖了 MCTS 算法及其变体 MCTSr，以及 MCTSr 如何提高 LLM 的准确性的详细信息。

理解蒙特卡洛树搜索

MCTS算法通过利用UCT公式，系统地平衡了探索（搜索新路径）和利用（优化已知路径）。

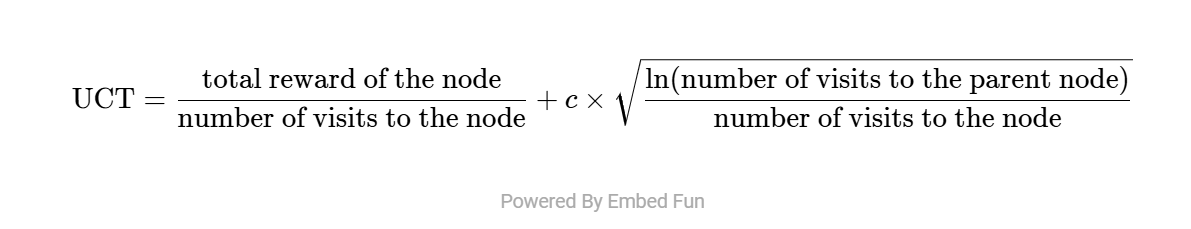
这个公式通过评估和选择搜索树中的节点来驱动MCTS的决策过程。

开发期限

• 表示节点的平均奖励。
• 鼓励算法优先考虑产生高回报的节点。

探索期限

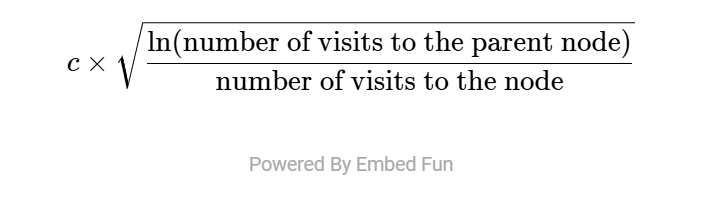
• 鼓励探索访问次数较少的节点。
• 由常数c控制，用于调节探索与利用之间的平衡。

探索与利用的动态平衡

探索常数c在蒙特卡洛树搜索中起着至关重要的作用，它决定了积极探索与保守利用之间的平衡：

• 较大的c：鼓励更积极地探索未访问的节点。
• 较小的c：倾向于更保守地利用高奖励节点。

c的选择对算法的性能有重大影响，并且应根据具体问题量身定制。以下是影响c选择的关键因素：

1. 搜索空间大小：较小的c适合奖励可预测的有限空间，而较大的c有助于在广阔、复杂的搜索空间中避免局部最优解。
2. 奖励不确定性：稳定的奖励倾向于较小的c以提高效率，而不确定、嘈杂的奖励则受益于较大的c以进行彻底探索。
3. 奖励规模：c应与奖励范围保持一致，以确保探索项保持有效，而不会掩盖利用项。
4. 时间/资源：资源充足时，较大的c允许更多探索以发现最优解，而资源有限时则需要较小的c以获得更快、更集中的结果。

正确调整c对于将MCTS适应不同应用至关重要。像井字棋这样的小型游戏搜索空间较小，优先利用，c的范围为[0.5, 1]。而像围棋和国际象棋这样的复杂游戏涉及非常大的搜索空间，优先探索，c的范围为[1, 2]。动态规划问题，如路径规划，需要一些探索，但通常奖励稳定，c的范围在[0.5, 1.5]之间。最后，随机奖励问题，如游戏AI，处理的是不确定的奖励分布，并增加了对探索的权重，c的范围为[1, 3]。

设计以避免过度探索或过度利用

随着MCTS的进行，搜索树中的节点数量迅速增加。新添加的节点开始时访问次数为零，而探索项确保它们不会被忽视。随着时间的推移，算法自然地平衡了探索与利用：

• 早期阶段：由于大多数节点访问次数较少，探索项占主导地位，鼓励对树进行广泛探索。
• 中后期阶段：随着节点积累更多访问次数，探索项的影响减弱，利用项占据优先地位。算法专注于高性能节点进行深入搜索。

关键见解：

1. 探索项影响的减弱和利用项影响的增强共同防止了节点值变得无法区分地大。
2. 调整c可以确保对不同问题特征的适应性，在探索与利用之间找到最佳平衡。

通过MCT自我精炼（MCTSr）增强数学推理能力

在论文《通过结合LLaMa-3 8B的蒙特卡洛树自我精炼访问GPT-4级别的数学奥林匹克解决方案：技术报告》中，作者介绍了MCT自我精炼（MCTSr）算法，这是蒙特卡洛树搜索（MCTS）的一种新颖变体。通过将MCTS与大型语言模型（LLM）相结合，MCTSr显著提升了复杂数学推理任务的性能。以下是研究的主要发现：

问题解决能力提高

MCTSr在多个基准数据集（包括GSM8K、MATH和数学奥林匹克问题）上解决数学问题时表现出显著改进。特别地，它在将解决方案推广到复杂的奥林匹克级别数学问题方面表现出色，而传统方法往往在这方面力不从心。

系统探索与自我提升的结合

MCTSr的强大之处在于其能够将系统探索与自我反思相结合：

• 自我精炼：通过迭代精炼解决方案，提高模型输出的准确性和可靠性。
• 自我评估：评估和选择最优解决方案路径，改善整体决策质量。

MCTS确保了对各种解决方案策略的结构化探索，而自我提升机制则不断推动答案质量的提高。

实验验证与有效性

大量实验验证了MCTSr的有效性：

• 迭代展开：与传统方法（如零样本思维链（CoT）和单次自我提升）相比，MCTSr的多轮迭代（如4次展开、8次展开）表现显著更优，将解决方案质量提高了20%–30%。
• 复杂度相关的增益：改进效果随问题复杂度而增加，在简单问题上实现显著性能提升，并在更具挑战性的问题中逐步接近最优解。
• 数据集结果：MCTSr在多个数据集上提高了准确性和成功率，特别是在处理难题时表现出色。

释放开源模型的潜力

研究强调了MCTSr如何缩小开源模型（如LLaMA-3 8B）和闭源模型（如GPT-4 Turbo）之间的性能差距。通过利用MCTSr，开源模型的数学推理能力接近甚至在某些情况下超越了先进专有模型的能力。

研究方法和验证

MCTSr算法在MCTS的基础上进行了多项针对LLM的增强：

MCTS的四个阶段：

• 选择：使用树上置信上界（UCT）识别最有前途的节点。
• 扩展：添加新节点以探索替代解决方案。
• 模拟：运行模拟以评估潜在结果。
• 反向传播：根据子节点的性能更新父节点。

MCTSr的增强：

• 动态剪枝：有效消除低潜力节点，优化搜索空间。
• 改进的UCT公式：通过精细调整平衡探索和利用。
• 自我精炼和自我评估：LLM迭代精炼其答案并评估其质量以提高输出准确性。

MCTSr基于解决方案的质量为每个节点分配一个奖励值（Q值）。使用UCT，算法动态选择具有最佳探索和利用平衡的节点进行进一步精炼。

Q值是什么？

Q值基于节点的奖励来量化节点（潜在解决方案）的“质量”。它结合了两个关键指标：

• 最小奖励：反映节点的最差性能。
• 平均奖励：反映节点的整体性能。

公式：

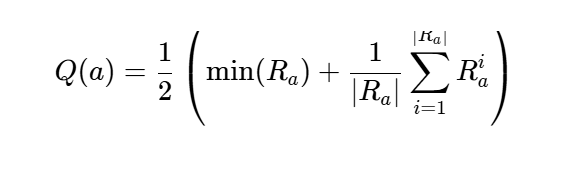
其中Ra是节点aaa的奖励集合。这个公式在平衡对不良结果的敏感性的同时，也考虑了整体质量。

Q值是如何计算的？

奖励来源：

• 大型语言模型（LLM）通过自我评估解决方案来生成奖励值。
• 奖励值的范围从-100到100，确保了一个广泛的评估范围。

采样策略：

• 重复采样：进行多次评估以减少噪声。
• 严格的评分约束：设计提示以确保进行客观评估。
• 满分抑制：对超过阈值（例如95）的分数进行封顶，以避免偏差。

反向传播：

Q值从子节点传播到父节点，更新整体解决方案的质量。反向传播公式综合了父节点和子节点的表现：

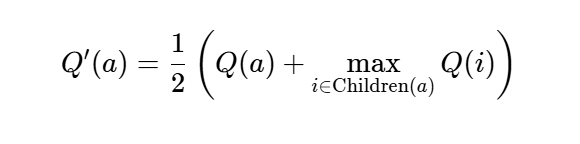
MCTSr利用UCT进行节点选择。

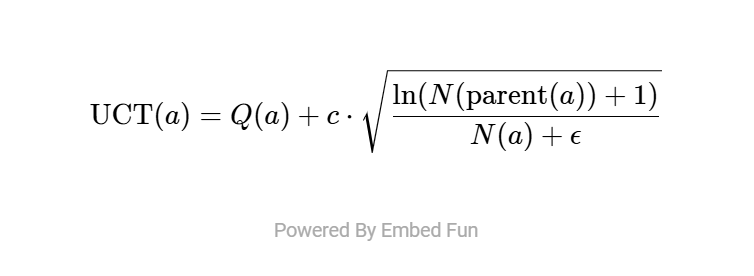
• Q(a)：节点a的质量。
• N(a)：节点a的访问次数。
• c：探索常数。
• ϵ：防止除以零的小常数。

这一机制通过平衡对高奖励节点的利用和对访问不足节点的探索，确保了最优决策的制定。

蒙特卡洛树搜索（MCTS）算法通过迭代循环的精炼和优化，增强了大型语言模型（LLM）的问题解决能力。以下是该过程的实用分步详解：

1. 以基本的“我不知道”回答作为初始种子答案开始。
2. 提示LLM对种子答案进行批判，并提供改进建议。
3. 根据LLM的反馈，生成三个精炼后的答案。
4. 随机选择一个改进后的答案，并让LLM对其质量进行评分。
5. 根据分数和访问统计信息，为所有节点计算树的置信上界（UCT）。
6. 确定具有最高UCT的节点，并对其进行进一步探索，从而有效地将搜索引导向最有前途的答案。
7. 通过建议、迭代改进和评分循环创建新节点，持续此过程，直到获得高质量的解决方案。