线性回归有多种类型：最小二乘法方法构成了其基础，从经典的普通最小二乘法（OLS）到带有正则化以防止过拟合的岭回归。然后还有套索回归，它采用了一种独特的方法，可以自动选择重要因素而忽略其他因素。弹性网络则结合了两者的优点，将套索回归的特征选择与岭回归处理相关特征的能力相结合。

不过许多文章将这些方法视为基本相同，只是进行了微小的调整。它们让人感觉在这些方法之间切换就像更改代码中的一个设置一样简单，但实际上每种方法都使用了不同的方法来解决它们的优化问题！

虽然OLS和岭回归可以直接通过矩阵运算来解决，但套索回归和弹性网络则需要不同的方法——一种称为坐标下降法的迭代方法。在这里，我们将通过清晰的可视化来探索这个算法是如何工作的。

定义

套索回归（Lasso Regression）

套索回归（Least Absolute Shrinkage and Selection Operator）是线性回归的一种变体，它在模型中添加了一个惩罚项。与线性回归一样，它也使用线性方程来预测数值。然而，套索回归还有一种方法可以将某些因素的重要性降为零，这使得它在两个主要任务中非常有用：进行预测和识别最重要的特征。

弹性网络回归（Elastic Net Regression）

弹性网络回归是岭回归和套索回归的结合，它综合了两者的惩罚项。名字“弹性网络”来源于物理学：就像弹性网络可以拉伸但仍然保持其形状一样，这种方法在适应数据的同时保持了结构。

该模型平衡了三个目标：最小化预测误差、保持系数较小（类似于套索回归），以及防止任何系数变得过大（类似于岭回归）。要使用这个模型，就像标准线性回归一样，将数据的特征值输入到线性方程中即可。

弹性网络的主要优点是，当特征相关时，它倾向于将特征作为一个整体保留或移除，而不是从组中随机选择一个特征。

所用数据集

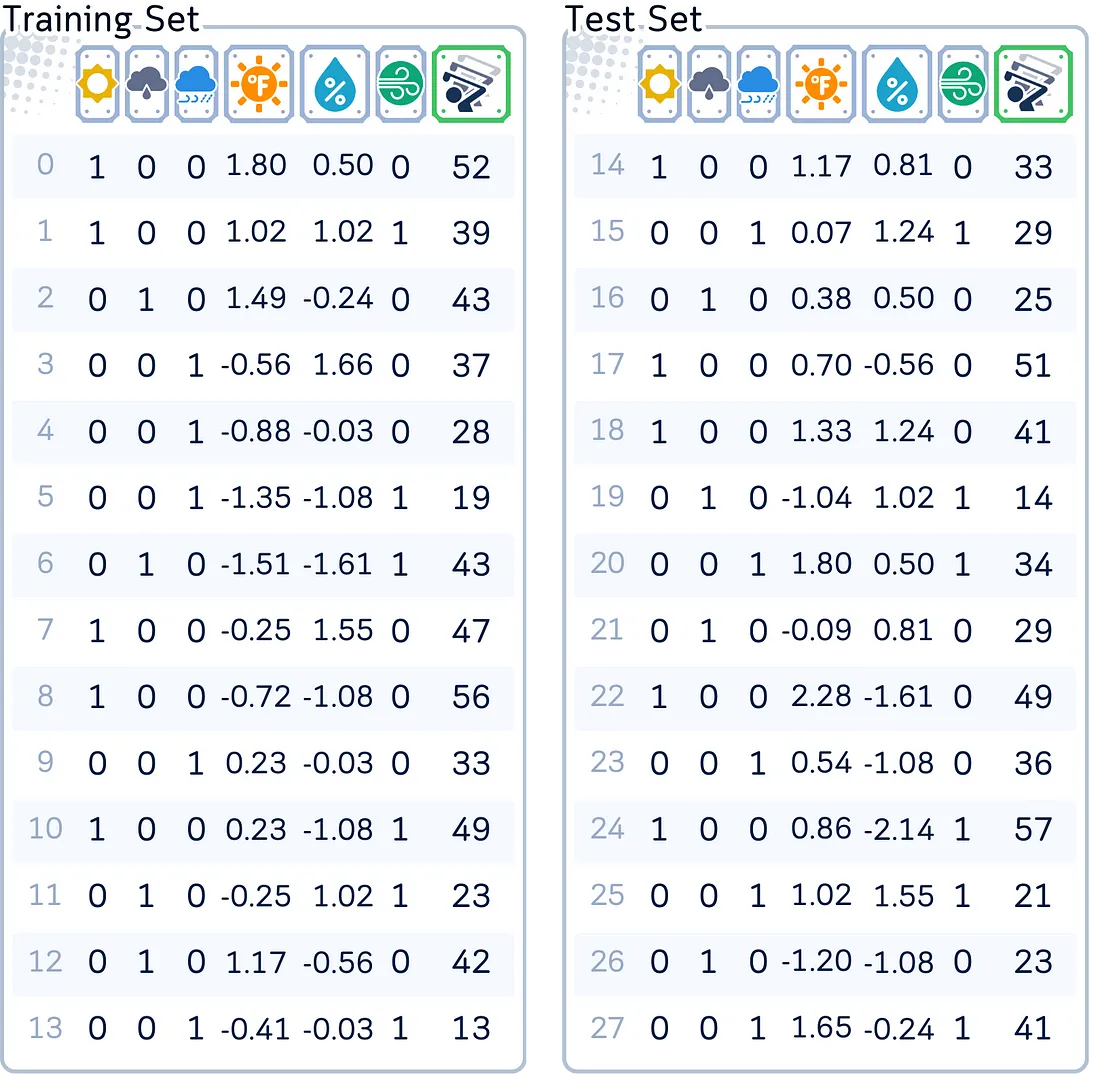
为了阐述我们的概念，我们将使用标准数据集来预测特定日期到访的高尔夫球手数量，该数据集使用的特征包括天气状况、温度、湿度和风力条件等。

为了使套索回归和弹性网络回归都能有效地工作，我们需要对数值特征进行标准化（使它们的尺度具有可比性），并对分类特征应用独热编码，因为这两种模型的惩罚项都对特征尺度敏感。

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
# Create dataset
data = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 
                'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 
                'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temperature': [85, 80, 83, 70, 68, 65, 64, 72, 69, 75, 75, 72, 81, 71, 81, 74, 76, 78, 82, 
                   67, 85, 73, 88, 77, 79, 80, 66, 84],
    'Humidity': [85, 90, 78, 96, 80, 70, 65, 95, 70, 80, 70, 90, 75, 80, 88, 92, 85, 75, 92, 
                 90, 85, 88, 65, 70, 60, 95, 70, 78],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, 
             True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 
                    14, 34, 29, 49, 36, 57, 21, 23, 41]
}
# Process data
df = pd.get_dummies(pd.DataFrame(data), columns=['Outlook'])
df['Wind'] = df['Wind'].astype(int)
# Split data
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Scale numerical features
numerical_cols = ['Temperature', 'Humidity']
ct = ColumnTransformer([('scaler', StandardScaler(), numerical_cols)], remainder='passthrough')
# Transform data
X_train_scaled = pd.DataFrame(
    ct.fit_transform(X_train),
    columns=numerical_cols + [col for col in X_train.columns if col not in numerical_cols],
    index=X_train.index
)
X_test_scaled = pd.DataFrame(
    ct.transform(X_test),
    columns=X_train_scaled.columns,
    index=X_test.index
)

主要机制

套索回归和弹性网络回归通过从数据中构建一条直线（或超平面）来预测数值，同时以不同的方式控制系数的大小：

这两种模型都通过平衡预测准确性和系数控制来找到最佳的直线。它们致力于使实际值和预测值之间的差距最小化，同时通过惩罚项来控制系数。

在套索回归中，惩罚项（由λ控制）可以将系数精确地缩小到零，从而完全移除特征。弹性网络则结合了两种类型的惩罚项：一种可以移除特征（类似于套索回归），另一种则将相关特征组一起缩小。这两种惩罚项之间的混合程度由l1_ratio（α）控制。

为了预测新的答案，这两种模型都会将每个输入乘以其系数（如果不为零），然后将它们相加，再加上一个起始数（截距/偏置）。当特征相关时，弹性网络通常会保留比套索回归更多的特征，但系数更小。

惩罚项的强度会影响模型的行为：

• 在套索回归中，较大的λ意味着更多的系数会变成零。
• 在弹性网络中，λ控制总体惩罚项的强度，而α则决定特征移除和系数缩小之间的平衡。
• 当惩罚项非常小时，这两种模型的行为会更接近于标准的线性回归。

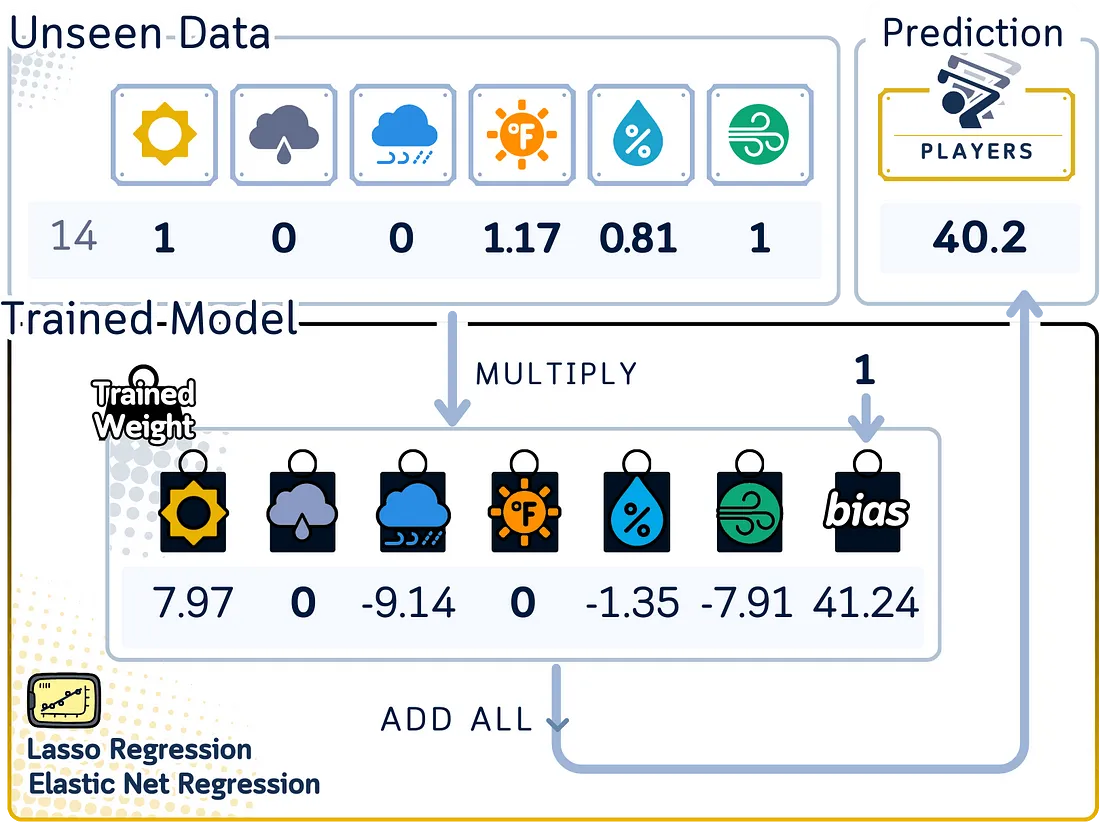
训练步骤

让我们来探讨一下套索回归和弹性网络如何使用坐标下降算法从数据中学习的。虽然这些模型有着复杂的数学基础，但我们将重点关注理解坐标下降，这是一种高效的优化方法，使得计算更加实用和直观。

套索回归的坐标下降法

套索回归的优化问题如下：

以下是坐标下降法通过每次更新一个特征来找到最优系数的方式：

首先，将模型的所有系数初始化为零。为正则化参数设置一个固定值，该参数将控制惩罚项的强度。

计算所有目标值的均值，以此作为初始偏置。

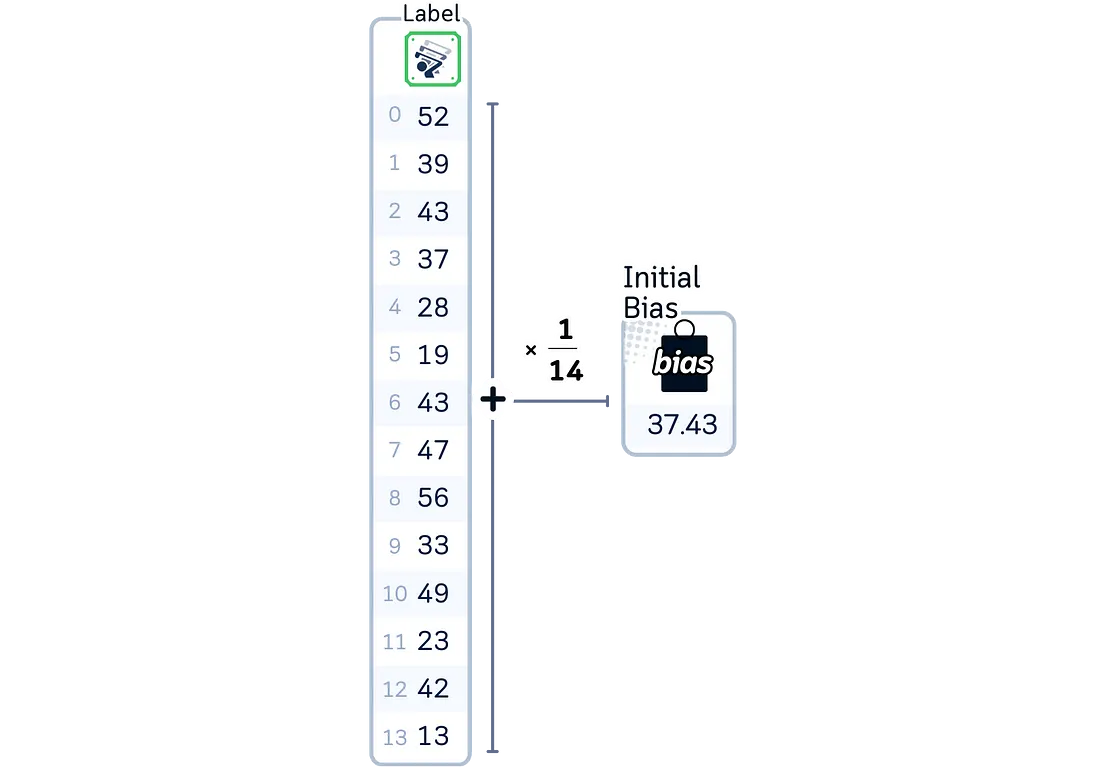
为了更新第一个系数（在我们的例子中是‘sunny’）：

使用加权和来计算如果不使用这个特征模型会预测出什么结果。

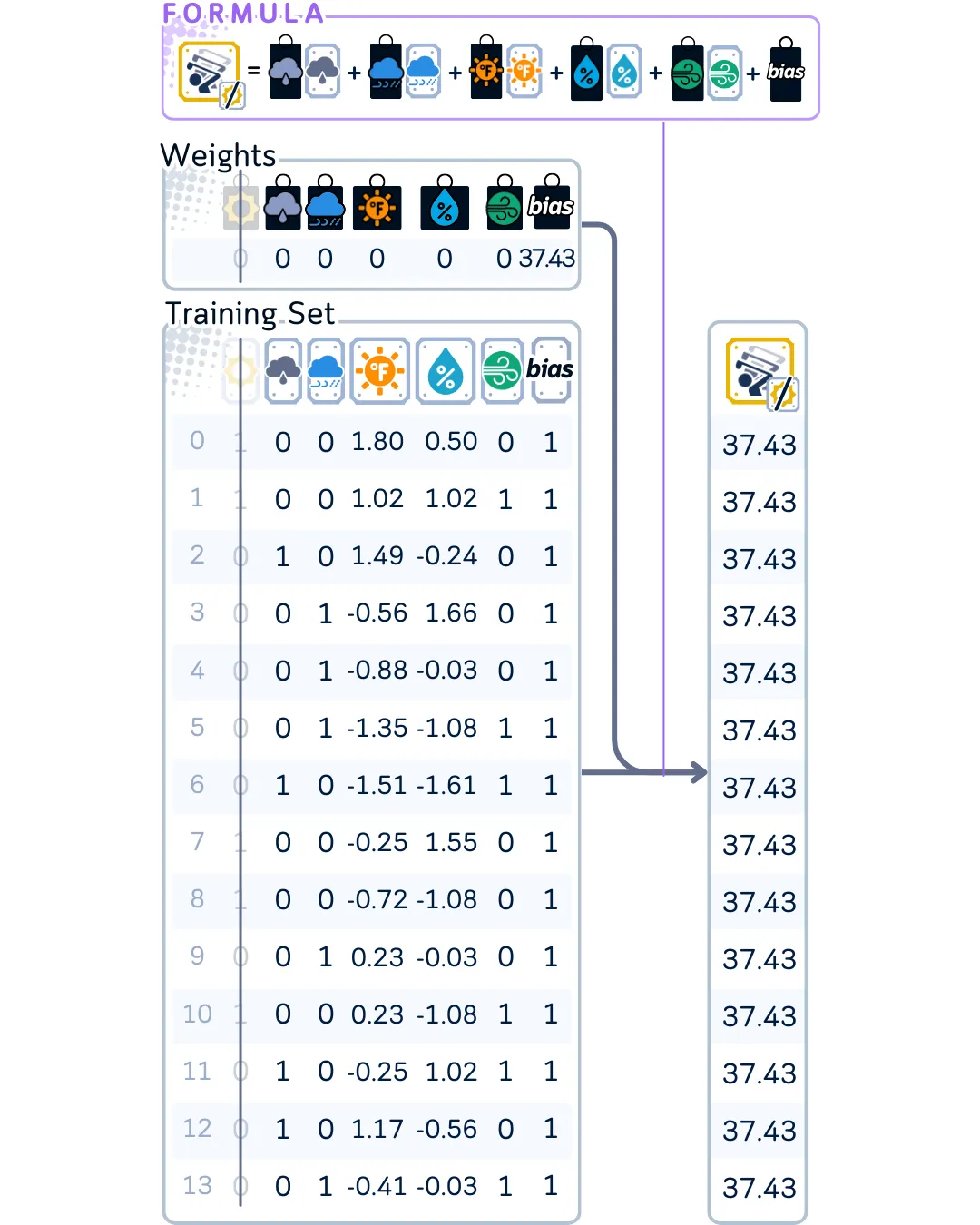
计算部分残差，这些预测值与实际值之间的差距。使用这个值来计算临时系数。

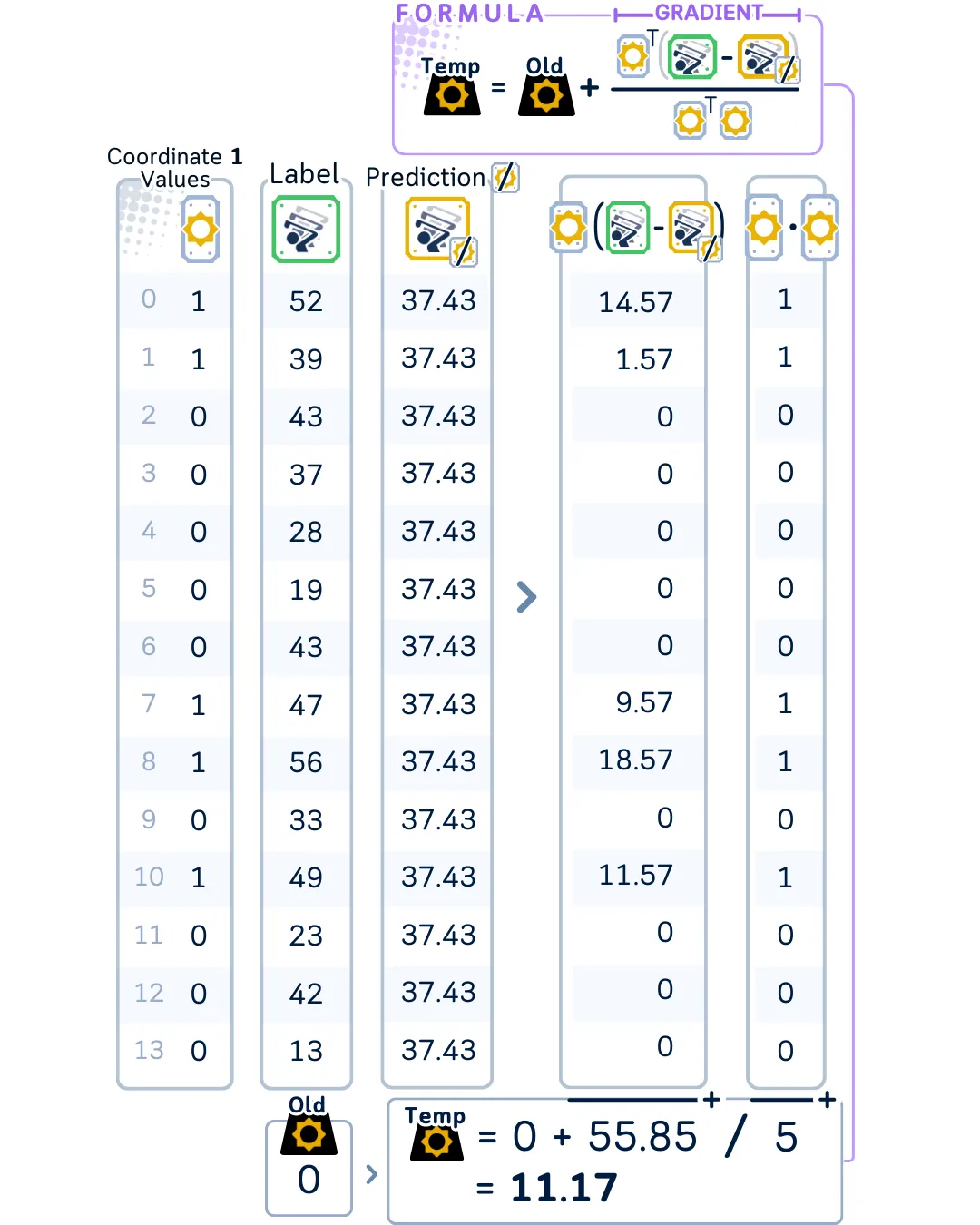
对这个临时系数应用套索收缩（软阈值化）以获得这步的最终系数。

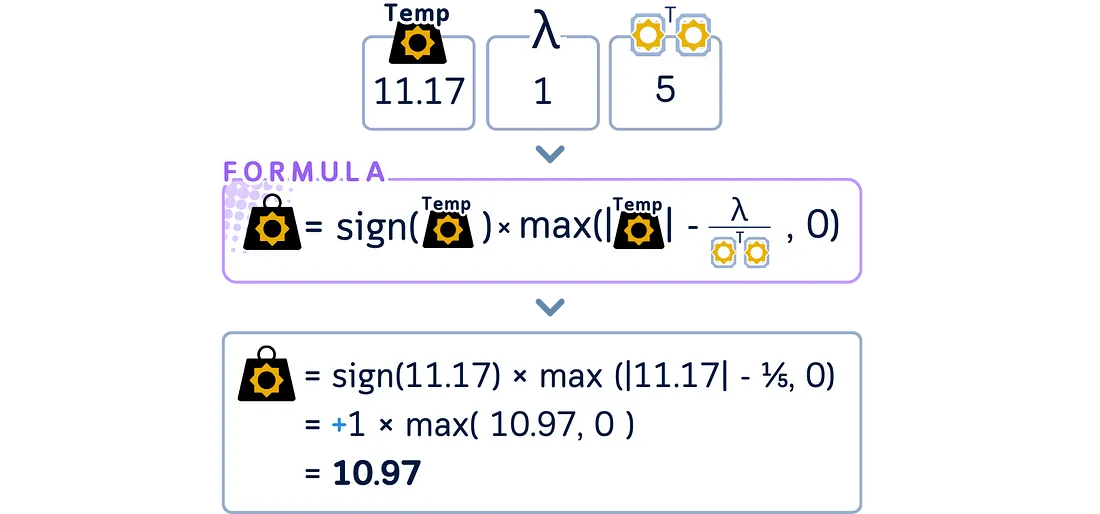
逐一遍历剩余的每个系数，重复相同的更新过程。在每次更新期间计算预测值时，使用所有其他系数的最新更新值。

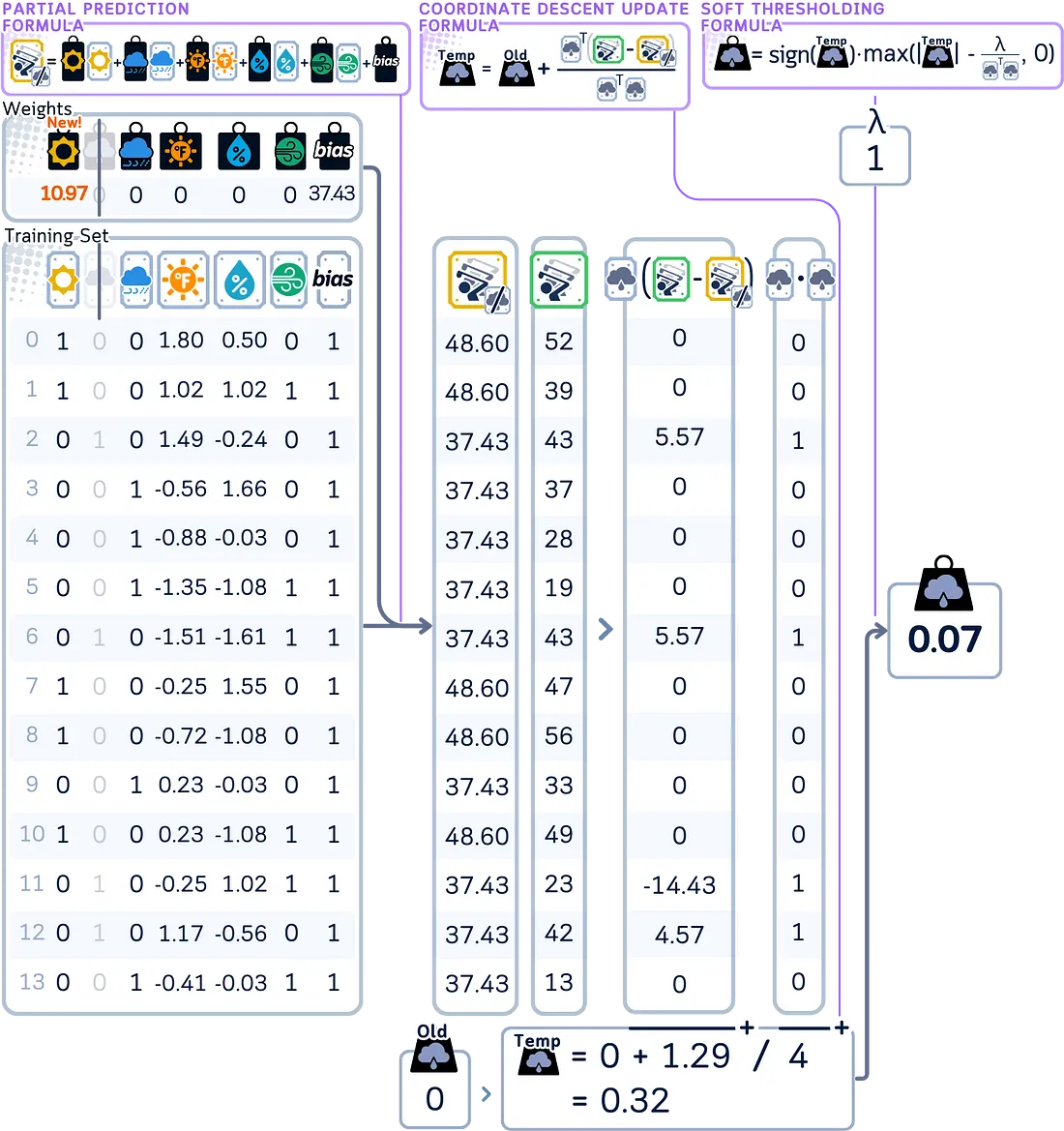
import numpy as np
# Initialize bias as mean of target values and coefficients to 0
bias = np.mean(y_train)
beta = np.zeros(X_train_scaled.shape[1])
lambda_param = 1
# One cycle through all features
for j, feature in enumerate(X_train_scaled.columns):
    # Get current feature values
    x_j = X_train_scaled.iloc[:, j].values
    # Calculate prediction excluding the j-th feature
    y_pred_no_j = bias + X_train_scaled.values @ beta - x_j * beta[j]
    # Calculate partial residuals
    residual_no_j = y_train.values - y_pred_no_j
    # Calculate the dot product of x_j with itself (sum of squared feature values)
    sum_squared_x_j = np.dot(x_j, x_j)
    # Calculate temporary beta without regularization (raw update)
    beta_old = beta[j]
    beta_temp = beta_old + np.dot(x_j, residual_no_j) / sum_squared_x_j
    # Apply soft thresholding for Lasso penalty
    beta[j] = np.sign(beta_temp) * max(abs(beta_temp) - lambda_param / sum_squared_x_j, 0)
# Print results
print("Coefficients after one cycle:")
for feature, coef in zip(X_train_scaled.columns, beta):
    print(f"{feature:11}: {coef:.2f}")

通过计算当前模型使用所有特征进行预测的结果，然后返回更新偏置，根据这些预测值与实际值之间的平均差异来调整偏置。

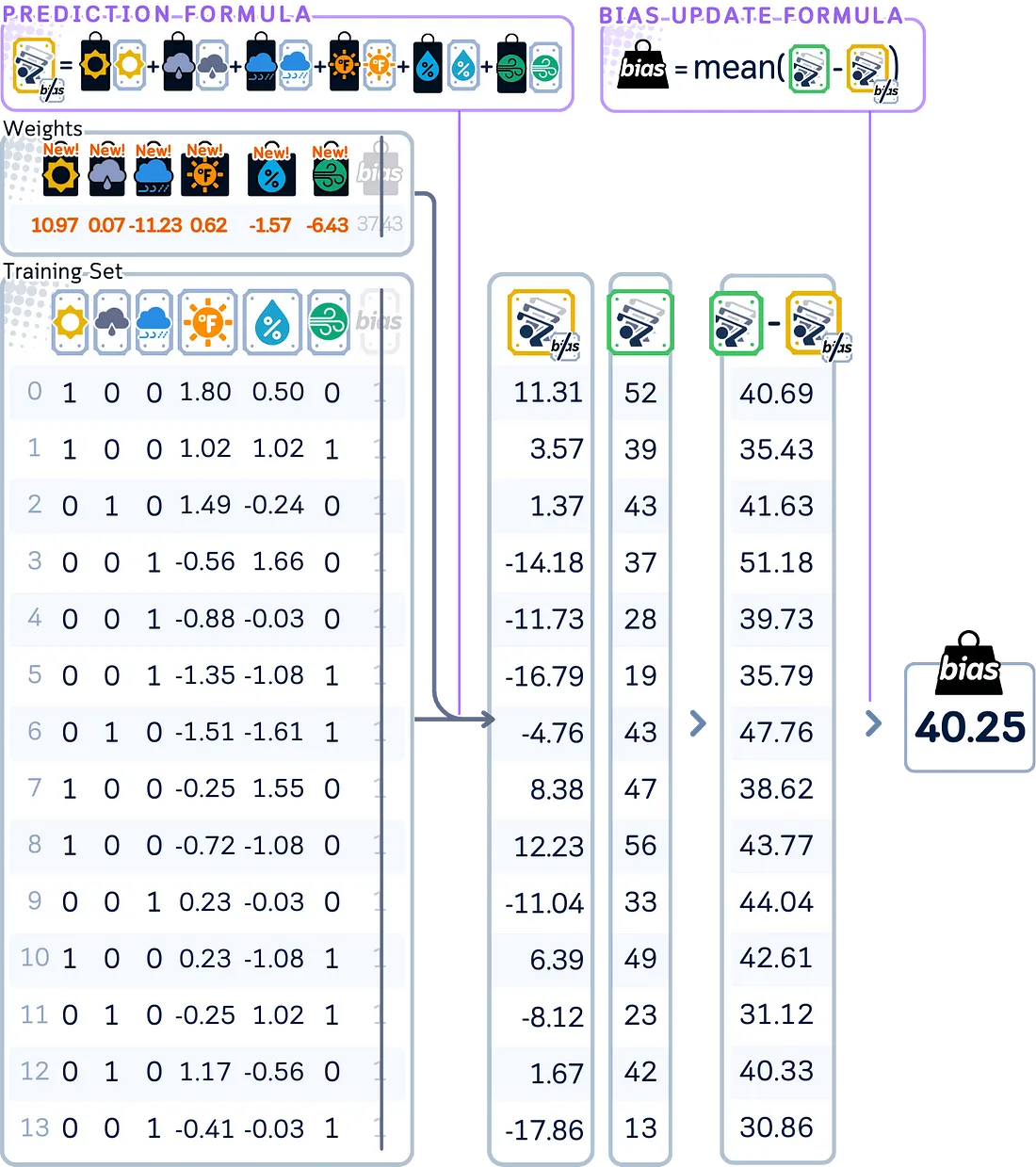
# Update bias (not penalized by lambda)
y_pred = X_train_scaled.values @ beta  # only using coefficients, no bias
residuals = y_train.values - y_pred
bias = np.mean(residuals)  # this replaces the old bias

检查模型是否已经收敛，这可以通过达到允许的最大迭代次数或者观察到系数不再发生显著变化来判断。如果模型尚未收敛，则返回第3步并重复该过程。

from sklearn.linear_model import Lasso
# Fit Lasso from scikit-learn
lasso = Lasso(alpha=1) # Default value is 1000 cycle
lasso.fit(X_train_scaled, y_train)
# Print results
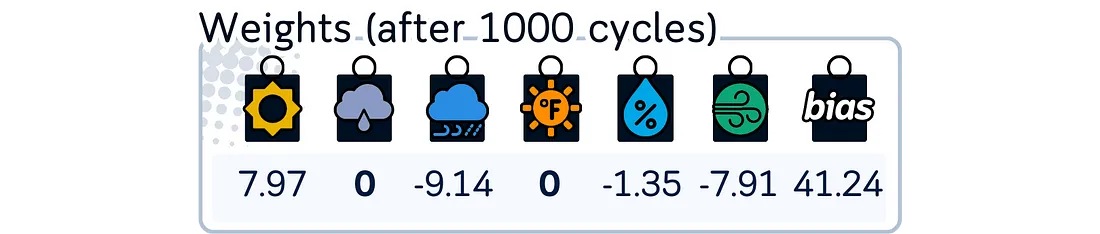
print("\nCoefficients after 1000 cycles:")
print(f"Bias term  : {lasso.intercept_:.2f}")
for feature, coef in zip(X_train_scaled.columns, lasso.coef_):
   print(f"{feature:11}: {coef:.2f}")

弹性网络回归的坐标下降法

弹性网络回归的优化问题如下：

弹性网络回归的坐标下降算法与套索回归类似，但在更新系数时会同时考虑两种惩罚项。其工作原理如下：

首先，将模型的所有系数初始化为零。设置两个固定值：一个用于控制特征移除（与套索回归类似），另一个用于一般的系数缩小（这是与套索回归的关键区别）。

计算所有目标值的均值，以此作为初始偏置。（与套索回归相同）

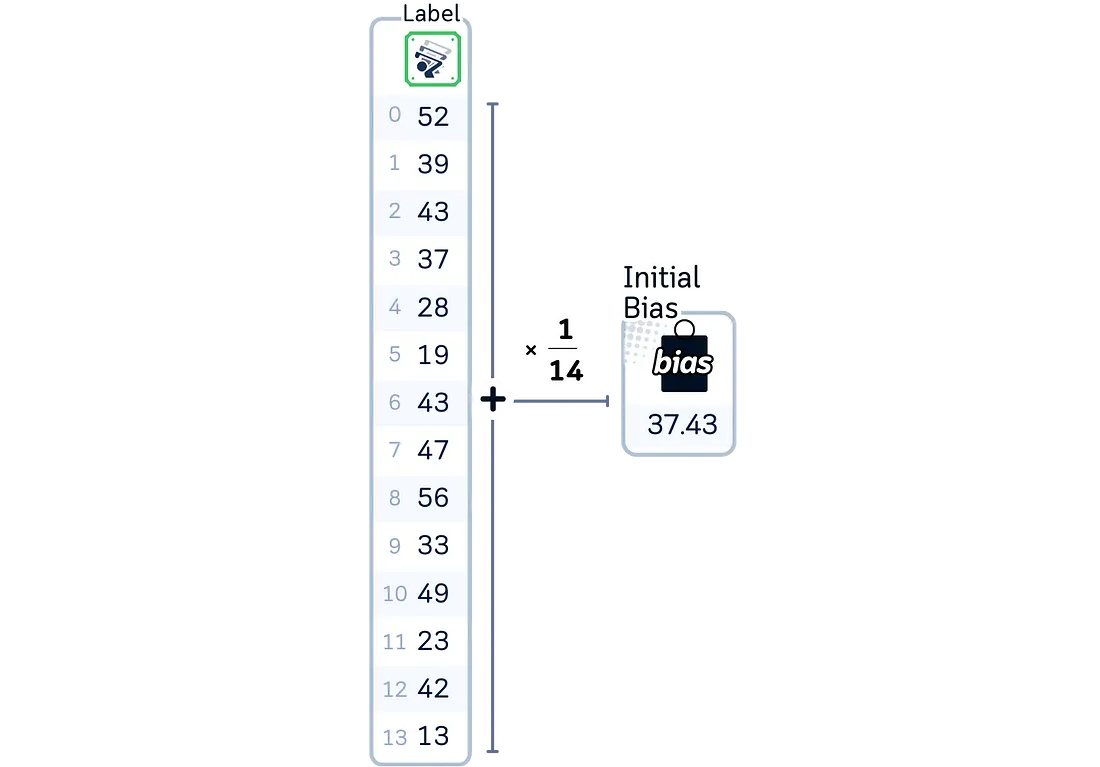
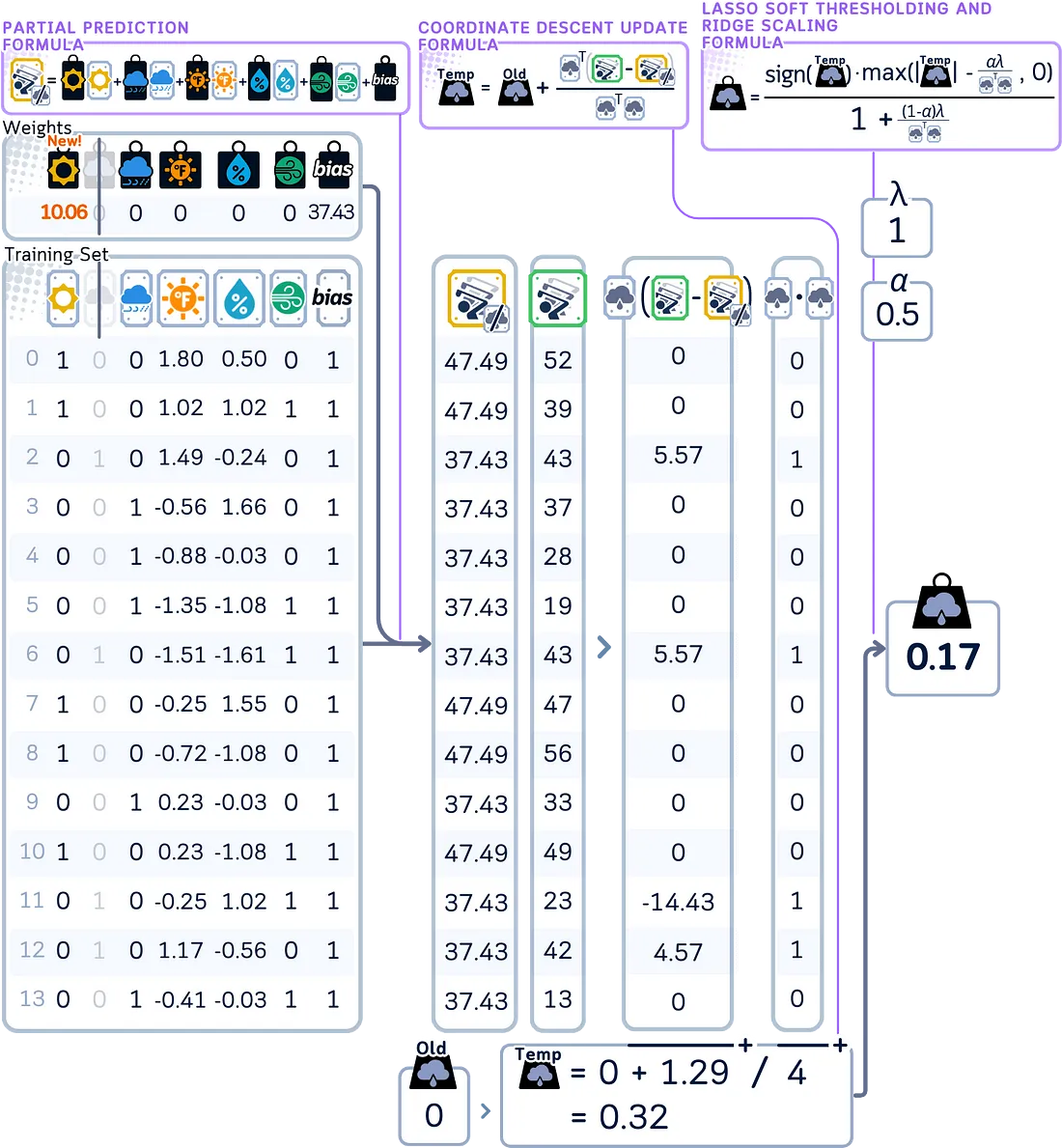
为了更新第一个系数：

使用加权和来计算如果不使用这个特征模型会预测出什么结果。（与套索回归相同）

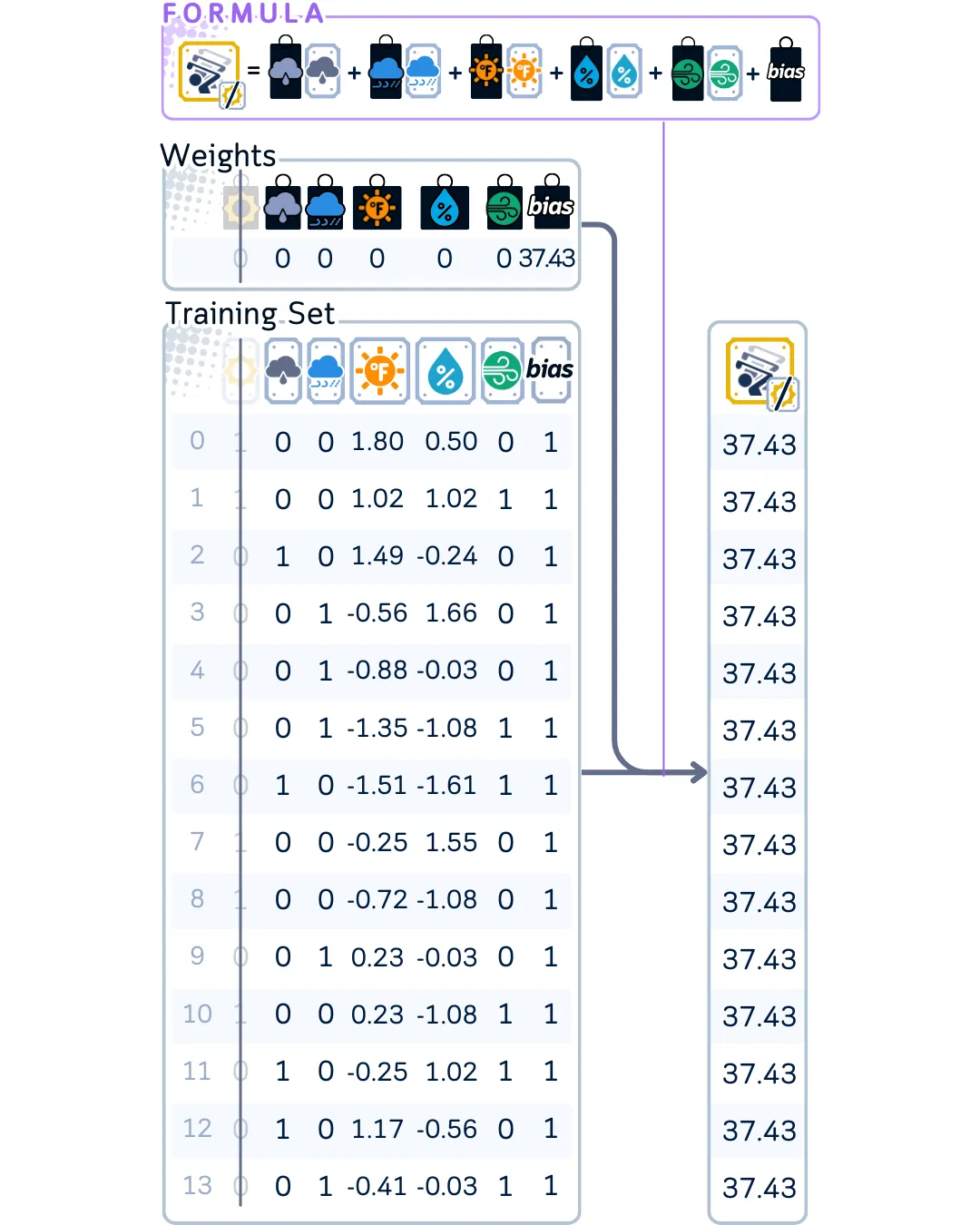
计算部分残差，这些预测值与实际值之间的差距。使用这个值来计算临时系数。（与套索回归相同）

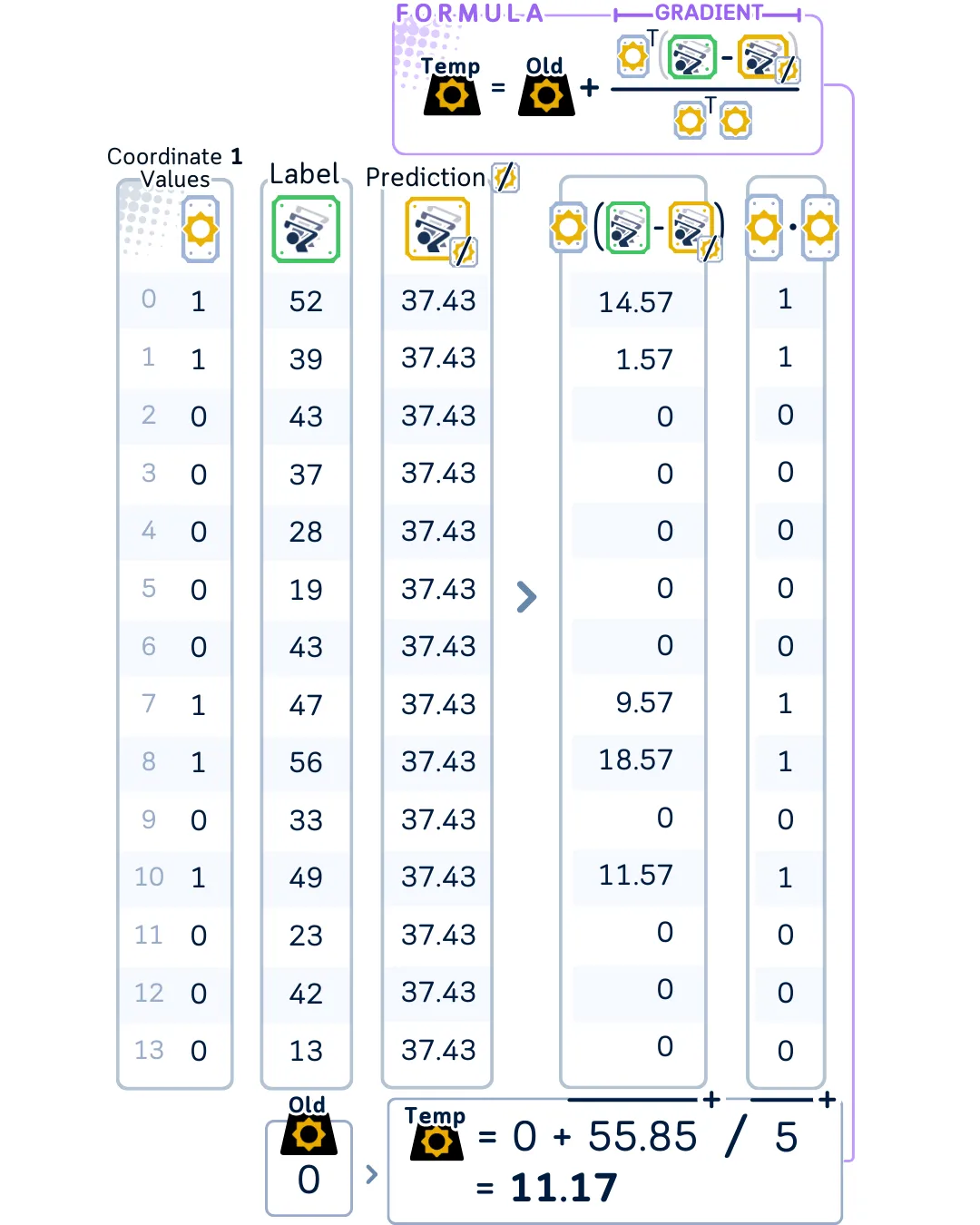
对于弹性网络回归，对这个临时系数同时应用软阈值化和系数缩小，以获得这一步的最终系数。这种组合效应是它与套索回归的主要区别。

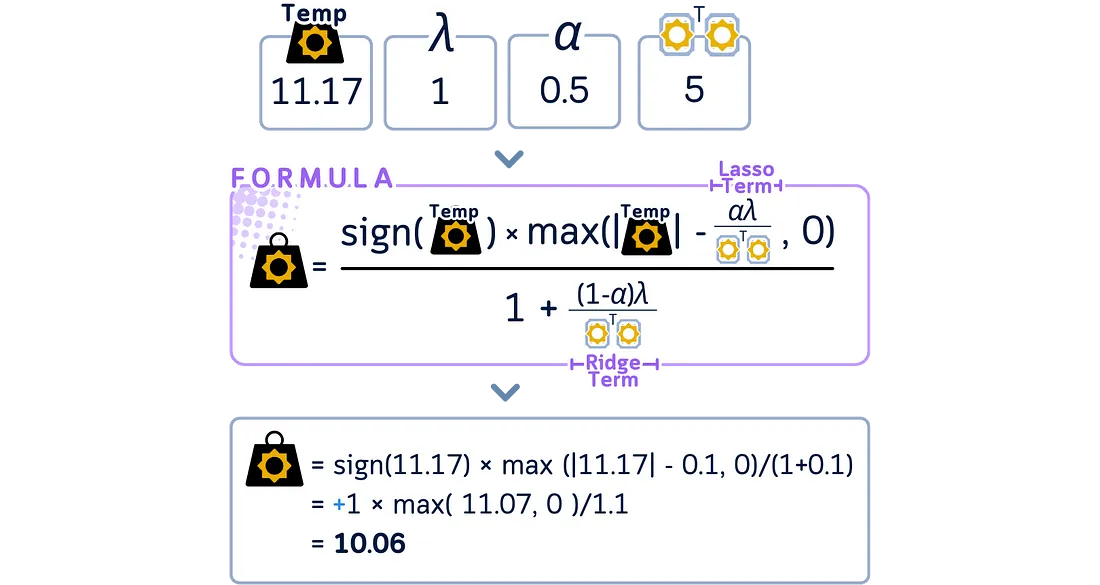
逐一遍历剩余的每个系数，重复相同的更新过程。在每次更新期间计算预测值时，使用所有其他系数的最新更新值。（过程与套索回归相同，但使用修改后的更新公式）

import numpy as np
# Initialize bias as mean of target values and coefficients to 0
bias = np.mean(y_train)
beta = np.zeros(X_train_scaled.shape[1])
lambda_param = 1
alpha = 0.5  # mixing parameter (0 for Ridge, 1 for Lasso)
# One cycle through all features
for j, feature in enumerate(X_train_scaled.columns):
    # Get current feature values
    x_j = X_train_scaled.iloc[:, j].values
    # Calculate prediction excluding the j-th feature
    y_pred_no_j = bias + X_train_scaled.values @ beta - x_j * beta[j]
    # Calculate partial residuals
    residual_no_j = y_train.values - y_pred_no_j
    # Calculate the dot product of x_j with itself (sum of squared feature values)
    sum_squared_x_j = np.dot(x_j, x_j)
    # Calculate temporary beta without regularization (raw update)
    beta_old = beta[j]
    beta_temp = beta_old + np.dot(x_j, residual_no_j) / sum_squared_x_j
    # Apply soft thresholding for Elastic Net penalty
    l1_term = alpha * lambda_param / sum_squared_x_j     # L1 (Lasso) penalty term
    l2_term = (1-alpha) * lambda_param / sum_squared_x_j # L2 (Ridge) penalty term
    
    # First apply L1 soft thresholding, then L2 scaling
    beta[j] = (np.sign(beta_temp) * max(abs(beta_temp) - l1_term, 0)) / (1 + l2_term)
# Print results
print("Coefficients after one cycle:")
for feature, coef in zip(X_train_scaled.columns, beta):
    print(f"{feature:11}: {coef:.2f}")

通过计算当前模型使用所有特征进行预测的结果来更新偏置，然后根据这些预测值与实际值之间的平均差异来调整偏置。（与套索回归相同）

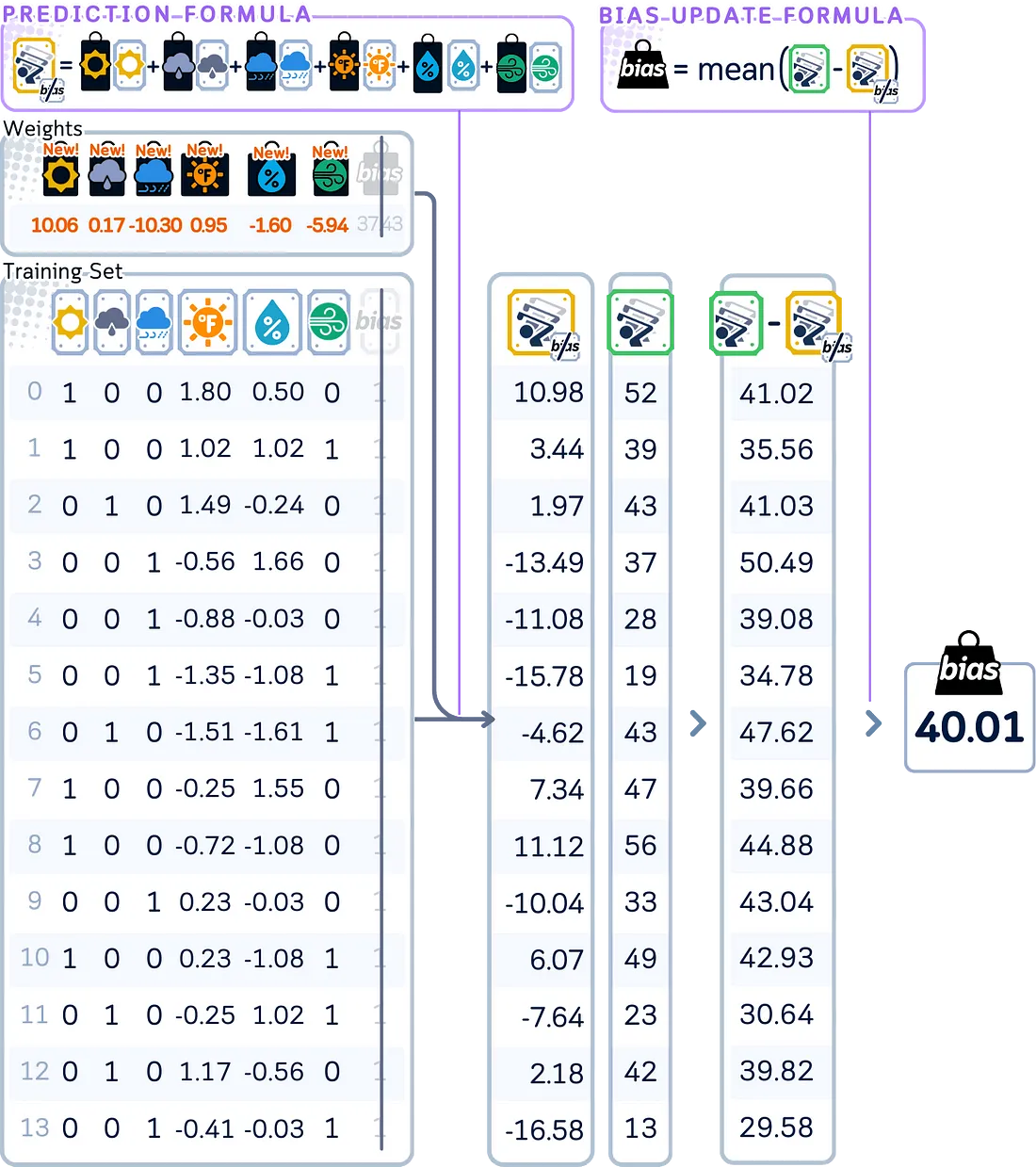
# Update bias (not penalized by lambda)
y_pred_with_updated_beta = X_train_scaled.values @ beta  # only using coefficients, no bias
residuals_for_bias_update = y_train.values - y_pred_with_updated_beta
new_bias = np.mean(y_train.values - y_pred_with_updated_beta)  # this replaces the old bias
print(f"Bias term  : {new_bias:.2f}")

检查模型是否已经收敛，这可以通过达到允许的最大迭代次数或者观察到系数不再发生显著变化来判断。如果模型尚未收敛，则返回第3步并重复该过程。

from sklearn.linear_model import ElasticNet
# Fit Lasso from scikit-learn
elasticnet = Lasso(alpha=1) # Default value is 1000 cycle
elasticnet.fit(X_train_scaled, y_train)
# Print results
print("\nCoefficients after 1000 cycles:")
print(f"Bias term  : {elasticnet.intercept_:.2f}")
for feature, coef in zip(X_train_scaled.columns, elasticnet.coef_):
   print(f"{feature:11}: {coef:.2f}")

测试步骤

预测过程与最小二乘法（OLS）相同——将新的数据点乘以系数：

套索回归

弹性网络回归

评估步骤

我们可以对所有数据点重复相同的过程。对于我们的数据集，以下是包含均方根误差（RMSE）的最终结果：

套索回归

弹性网络回归

关键参数

套索回归

套索回归使用坐标下降法来解决优化问题。以下是其关键参数：

• alpha (λ)：控制对大系数的惩罚强度。较高的值会迫使更多的系数变为零。默认值为1.0。
• max_iter：设置算法在搜索最佳结果时更新其解决方案的最大循环次数。默认值为1000。
• tol：设置算法在决定找到足够好的解决方案之前，系数需要变化多小。默认值为0.0001。

弹性网络回归

弹性网络回归结合了两种类型的惩罚，并且也使用坐标下降法。以下是其关键参数：

• alpha (λ)：同时控制两种惩罚的总体强度。较高的值意味着更强的惩罚。默认值为1.0。
• l1_ratio (α)：设置每种惩罚的使用程度。值为0时仅使用岭惩罚，而值为1时仅使用套索惩罚。0到1之间的值则同时使用两者。默认值为0.5。
• max_iter：坐标下降算法的最大迭代次数。默认值为1000次迭代。
• tol：优化收敛的容差，与套索回归类似。默认值为1e-4。

模型比较：OLS、Lasso、Ridge 和 Elastic Net

通过调整参数，我们可以使用弹性网络来探索不同类型的线性回归模型：

• 当alpha = 0时，我们得到普通最小二乘法（OLS）
• 当alpha > 0且l1_ratio = 0时，我们得到岭回归
• 当alpha > 0且l1_ratio = 1时，我们得到套索回归
• 当alpha > 0且0 < l1_ratio < 1时，我们得到弹性网络回归

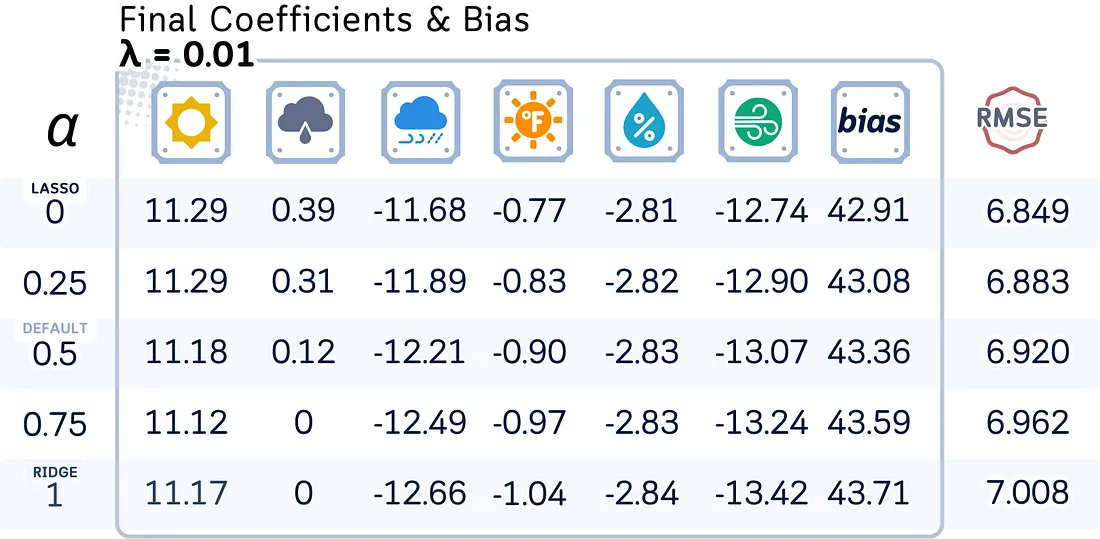
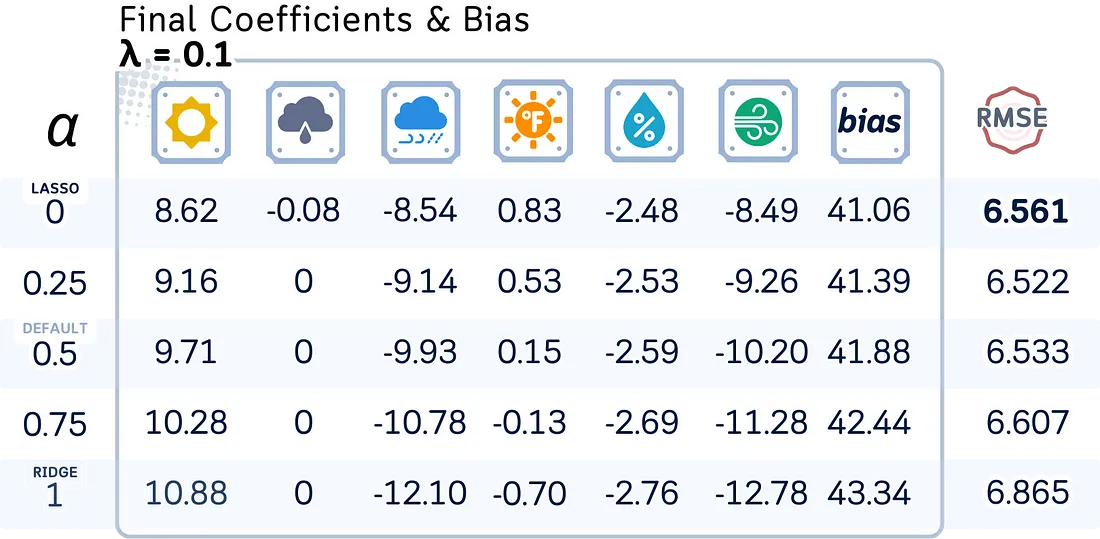
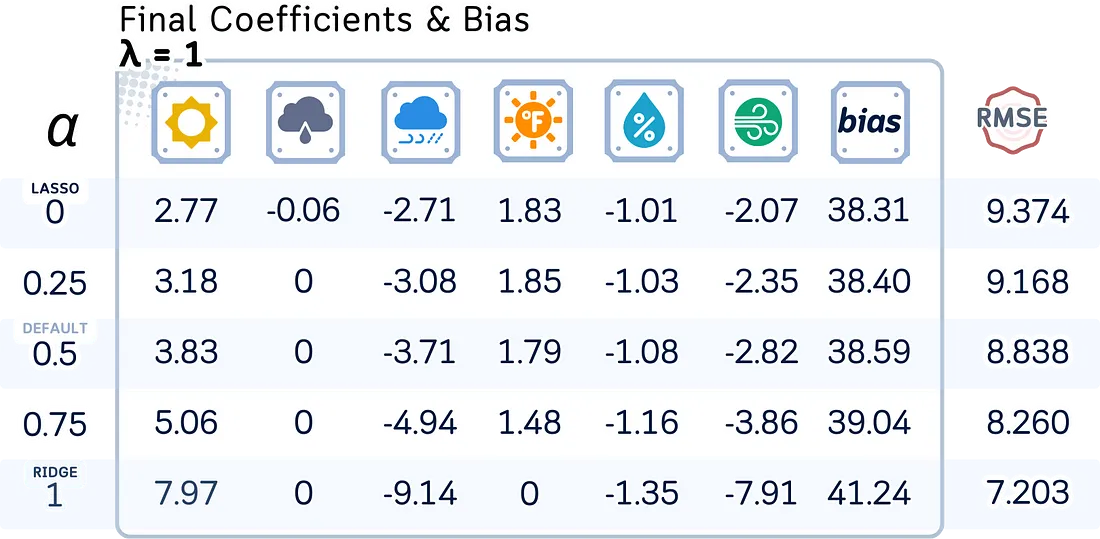
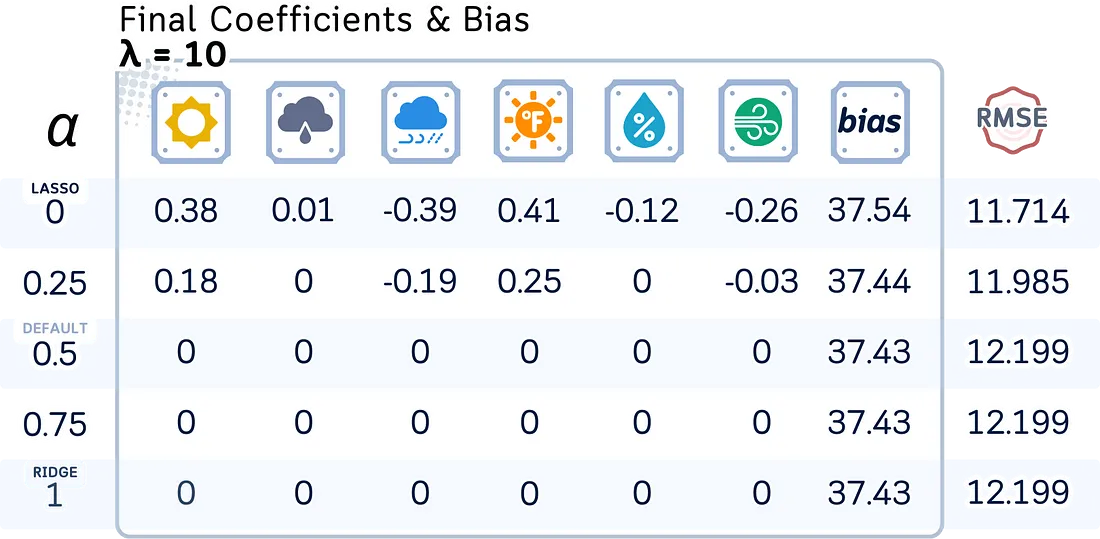
在实践中，探索一系列alpha值（如0.0001, 0.001, 0.01, 0.1, 1, 10, 100）和l1_ratio值（如0, 0.25, 0.5, 0.75, 1）是一个好主意，最好使用交叉验证来找到最佳组合。

接下来，让我们看看模型系数、偏置项和测试均方根误差（RMSE）如何随不同的正则化强度（λ）和混合参数（l1_ratio）而变化。

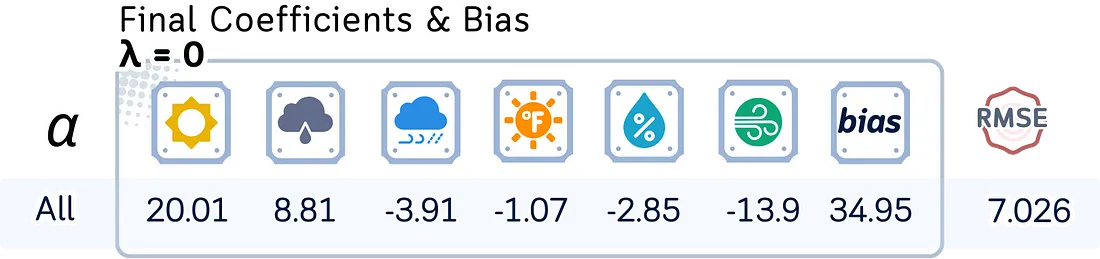
# Define parameters
l1_ratios = [0, 0.25, 0.5, 0.75, 1]
lambdas = [0, 0.01, 0.1, 1, 10]
feature_names = X_train_scaled.columns
# Create a dataframe for each lambda value
for lambda_val in lambdas:
    # Initialize list to store results
    results = []
    rmse_values = []
    
    # Fit ElasticNet for each l1_ratio
    for l1_ratio in l1_ratios:
        # Fit model
        en = ElasticNet(alpha=lambda_val, l1_ratio=l1_ratio)
        en.fit(X_train_scaled, y_train)
        
        # Calculate RMSE
        y_pred = en.predict(X_test_scaled)
        rmse = root_mean_squared_error(y_test, y_pred)
        
        # Store coefficients and RMSE
        results.append(list(en.coef_.round(2)) + [round(en.intercept_,2),round(rmse,3)])
    
    # Create dataframe with RMSE column
    columns = list(feature_names) + ['Bias','RMSE']
    df = pd.DataFrame(results, index=l1_ratios, columns=columns)
    df.index.name = f'λ = {lambda_val}'
    
    print(df)

注意：尽管弹性网络可以通过改变其参数来实现OLS、岭回归和套索回归的功能，但最好还是使用为每种回归类型专门设计的命令。在scikit-learn中，对于OLS使用LinearRegression，对于岭回归使用Ridge，对于套索回归使用Lasso。只有当你想要结合套索回归和岭回归的特殊功能时，才使用弹性网络。

Lasso和Elastic Net代码总结

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.compose import ColumnTransformer
from sklearn.metrics import root_mean_squared_error
from sklearn.linear_model import Lasso  #, ElasticNet
# Create dataset
data = {
    'Outlook': ['sunny', 'sunny', 'overcast', 'rain', 'rain', 'rain', 'overcast', 'sunny', 'sunny', 
                'rain', 'sunny', 'overcast', 'overcast', 'rain', 'sunny', 'overcast', 'rain', 'sunny', 
                'sunny', 'rain', 'overcast', 'rain', 'sunny', 'overcast', 'sunny', 'overcast', 'rain', 'overcast'],
    'Temperature': [85, 80, 83, 70, 68, 65, 64, 72, 69, 75, 75, 72, 81, 71, 81, 74, 76, 78, 82, 
                   67, 85, 73, 88, 77, 79, 80, 66, 84],
    'Humidity': [85, 90, 78, 96, 80, 70, 65, 95, 70, 80, 70, 90, 75, 80, 88, 92, 85, 75, 92, 
                 90, 85, 88, 65, 70, 60, 95, 70, 78],
    'Wind': [False, True, False, False, False, True, True, False, False, False, True, True, False, 
             True, True, False, False, True, False, True, True, False, True, False, False, True, False, False],
    'Num_Players': [52, 39, 43, 37, 28, 19, 43, 47, 56, 33, 49, 23, 42, 13, 33, 29, 25, 51, 41, 
                    14, 34, 29, 49, 36, 57, 21, 23, 41]
}
# Process data
df = pd.get_dummies(pd.DataFrame(data), columns=['Outlook'], prefix='', prefix_sep='', dtype=int)
df['Wind'] = df['Wind'].astype(int)
df = df[['sunny','overcast','rain','Temperature','Humidity','Wind','Num_Players']]
# Split data
X, y = df.drop(columns='Num_Players'), df['Num_Players']
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.5, shuffle=False)
# Scale numerical features
numerical_cols = ['Temperature', 'Humidity']
ct = ColumnTransformer([('scaler', StandardScaler(), numerical_cols)], remainder='passthrough')
# Transform data
X_train_scaled = pd.DataFrame(
    ct.fit_transform(X_train),
    columns=numerical_cols + [col for col in X_train.columns if col not in numerical_cols],
    index=X_train.index
)
X_test_scaled = pd.DataFrame(
    ct.transform(X_test),
    columns=X_train_scaled.columns,
    index=X_test.index
)
# Initialize and train the model
model = Lasso(alpha=0.1)  # Option 1: Lasso Regression (alpha is the regularization strength, equivalent to λ, uses coordinate descent)
#model = ElasticNet(alpha=0.1, l1_ratio=0.5)  # Option 2: Elastic Net Regression (alpha is the overall regularization strength, and l1_ratio is the mix between L1 and L2, uses coordinate descent)
# Fit the model
model.fit(X_train_scaled, y_train)
# Make predictions
y_pred = model.predict(X_test_scaled)
# Calculate and print RMSE
rmse = root_mean_squared_error(y_test, y_pred)
print(f"RMSE: {rmse:.4f}")
# Additional information about the model
print("\nModel Coefficients:")
for feature, coef in zip(X_train_scaled.columns, model.coef_):
    print(f"{feature:13}: {coef:.2f}")
print(f"Intercept    : {model.intercept_:.2f}")