旋转位置嵌入（RoPE）在近期的大型语言模型（LLM）中得到了广泛应用，用以编码位置信息，这些模型包括Meta的LLaMA和Google的PaLM。

在序列模型中，位置至关重要，而位置嵌入在基于Transformer的架构中发挥着关键作用。RoPE，即旋转位置嵌入，采用了一种巧妙的方法来同时融入相对和绝对位置信息。

重新审视注意力乘积

在介绍RoPE之前，让我们先回顾一下注意力机制的基础知识。注意力机制关注于成对关系：一个来自某个标记的查询向量q和另一个来自不同标记的键向量k。我们通过计算q和k的内积来获得注意力分数，这个内积对于位置嵌入的运作至关重要。

例如，为了获取标记对（1, 3）的注意力分数，我们从标记1中获取查询向量，从标记3中获取键向量。

我们首先从标记编码器中提取标记1的嵌入，然后通过位置+注意力编码器将这个嵌入及其位置信息输入进去。位置+注意力编码器会整合位置信息，并将结果投影以产生键向量。

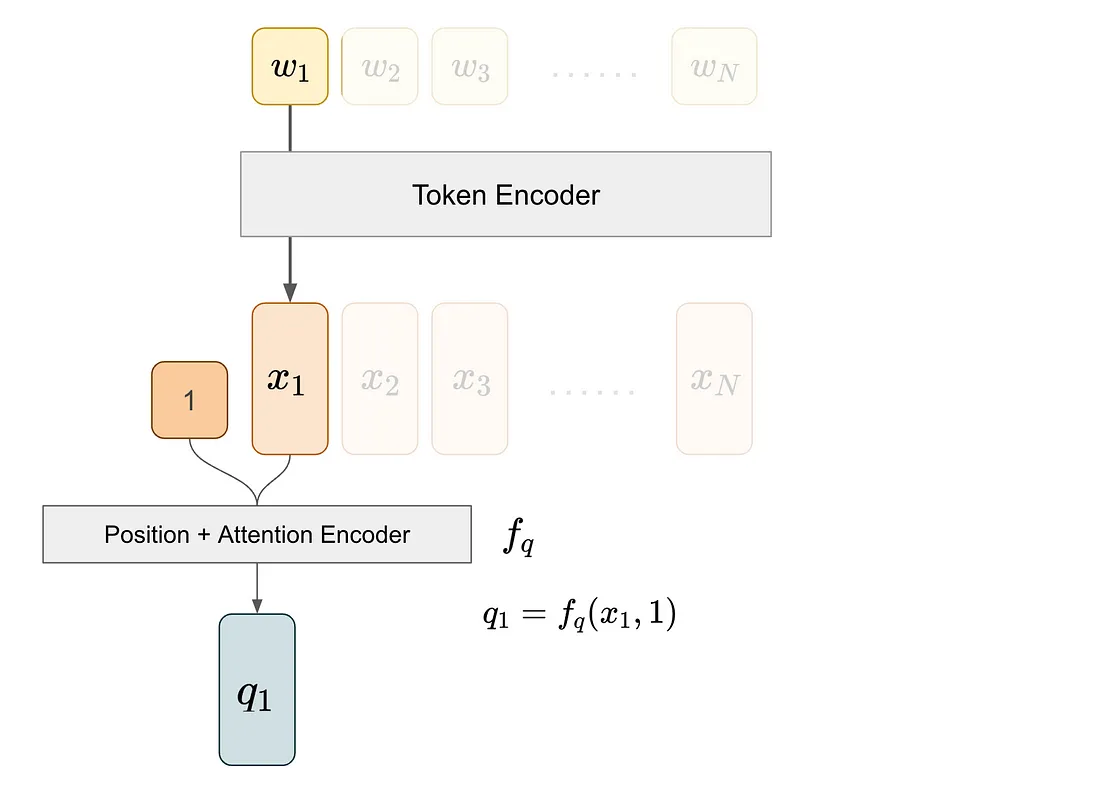
我们对第三个标记执行类似的过程，以获得k3，即与标记3对应的键向量。

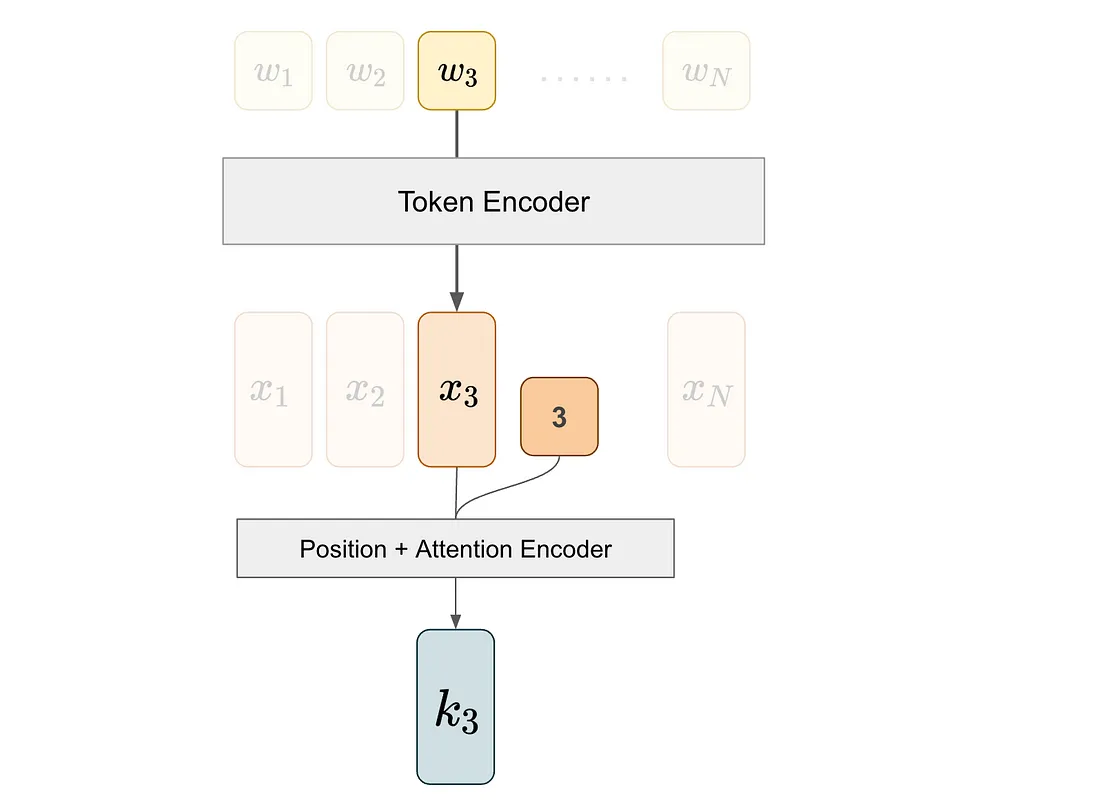
最后，我们计算q1和k3的内积，以确定(1, 3)对的注意力分数。在下面的等式中，尖括号<>表示内积，x代表标记嵌入，f代表注意力+位置编码器。

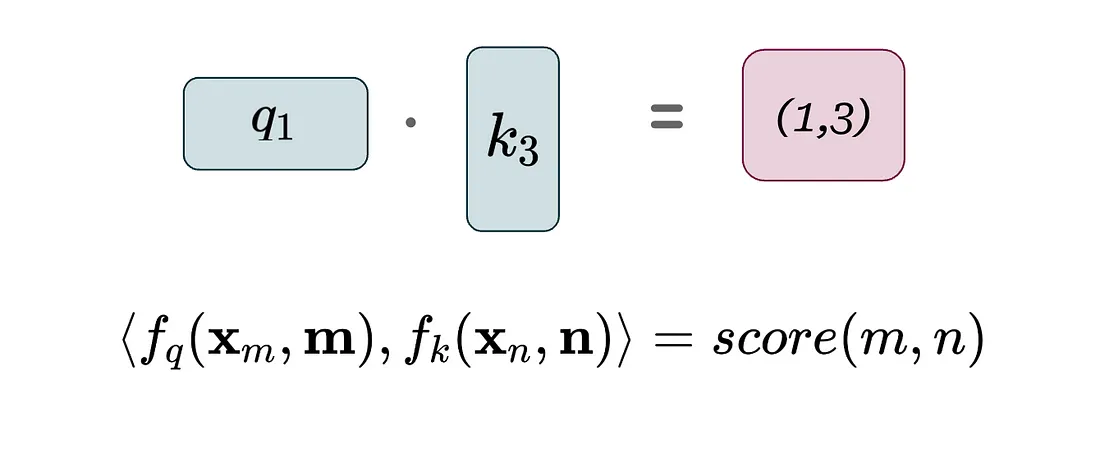
作者随后反思了这一公式，并意识到在这种设置中，相对位置信息是在内积之前编码的——这意味着它与标记嵌入固有地联系在一起。

他们自问：“是否有另一种方法，只有在我们需要注意力分数时——即在我们执行q,k内积的那一刻——才编码相对位置信息？”或者等价地说，q,k内积是否等价于另一个函数g，该函数仅将标记嵌入和它们的位置作为输入？

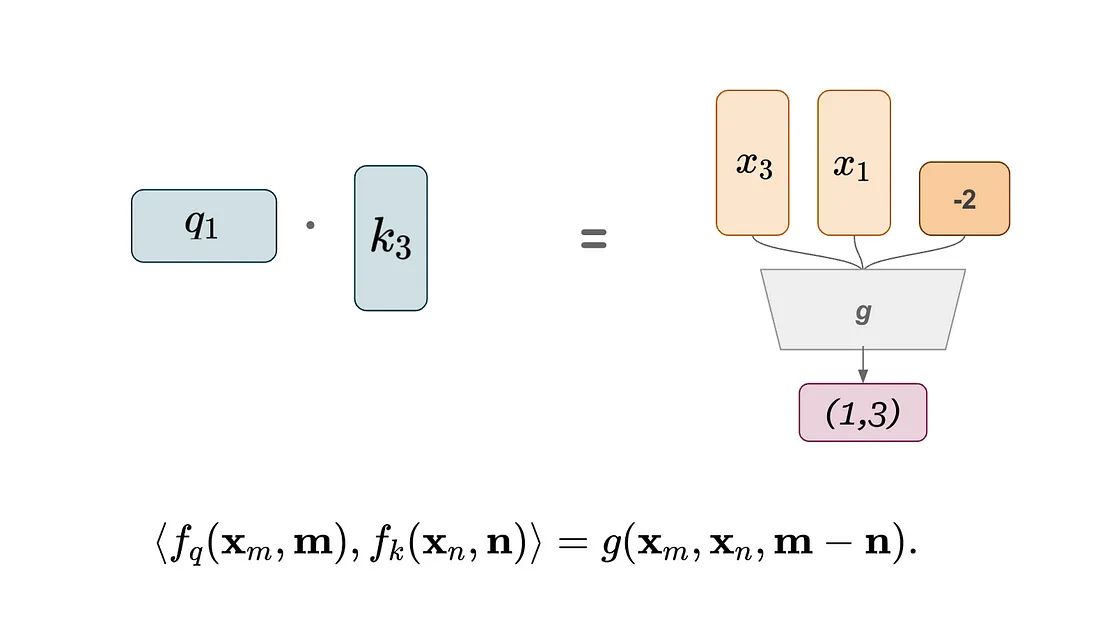
这就是RoPE位置嵌入发挥作用的地方。

RoPE的直观理解：一个2D简单案例

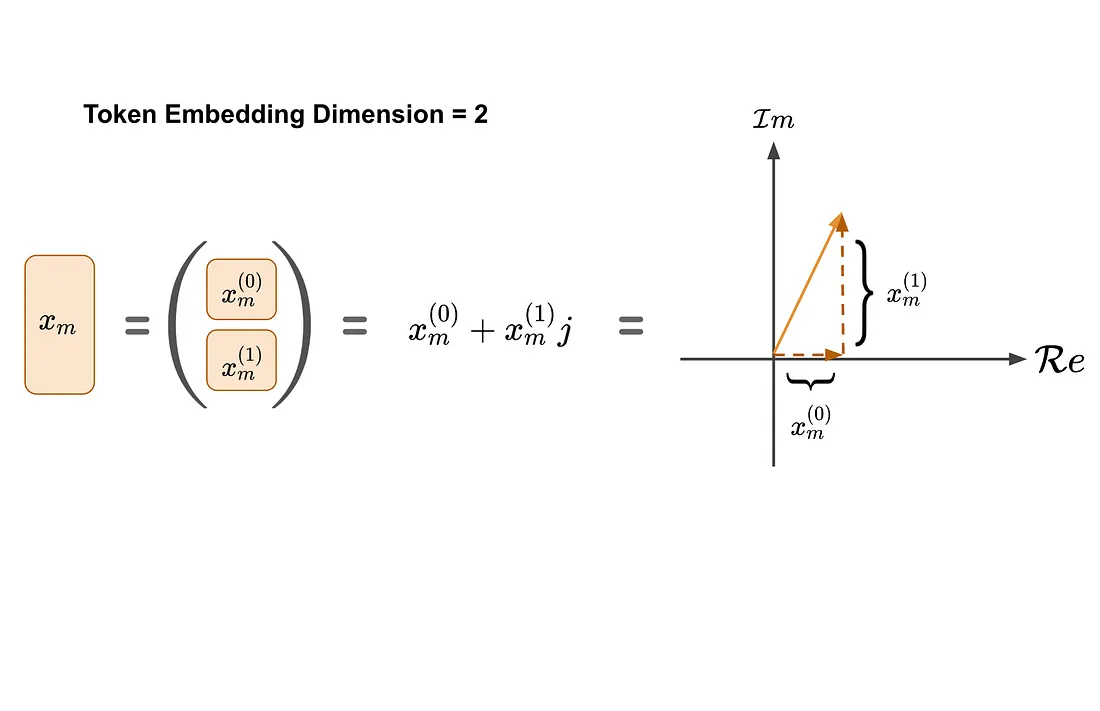
作者首先考虑了一个简单的2D案例，其中标记嵌入和注意力向量（查询、键）都存在于2D空间中。为了方便起见，这些2D向量也可以使用复数来表示（如图所示）。

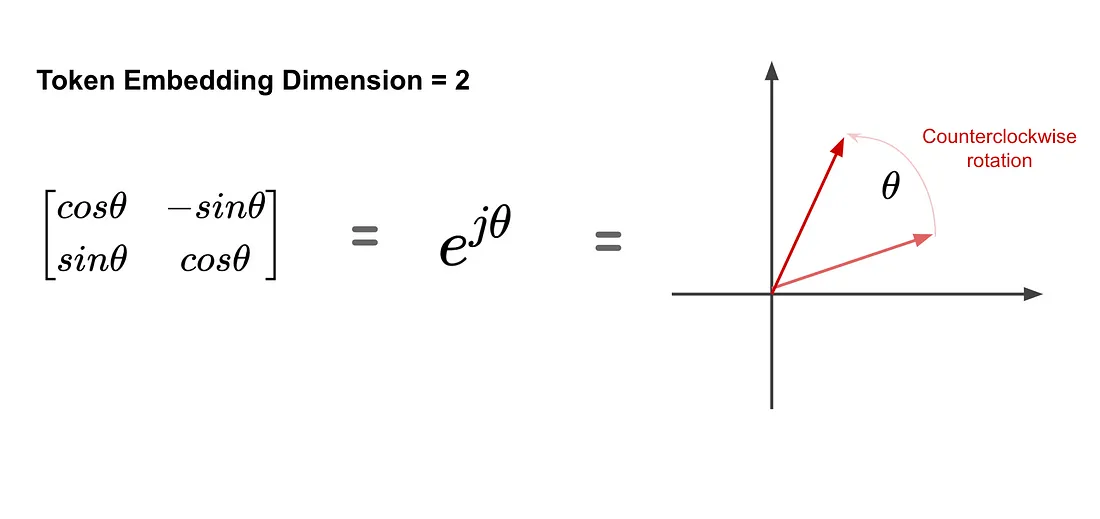
逆时针旋转矩阵既可以用矩阵形式表示，也可以用指数形式表示。

同样地，我们可以使用二维矩阵来表示从标记嵌入到键向量或查询向量的投影。

作者发现，满足以下条件的一种可能解决方案（即f和g的变换）是：

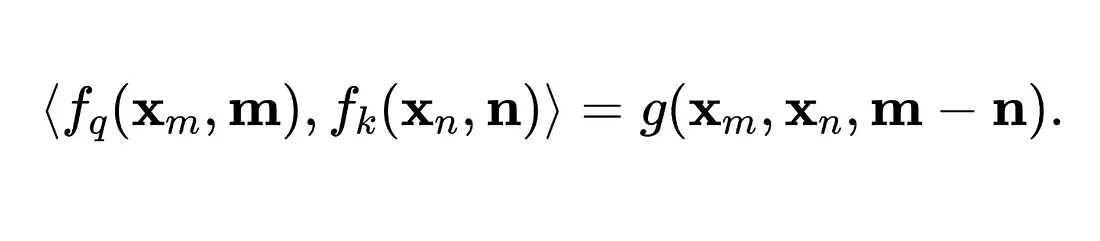
具有以下形式：

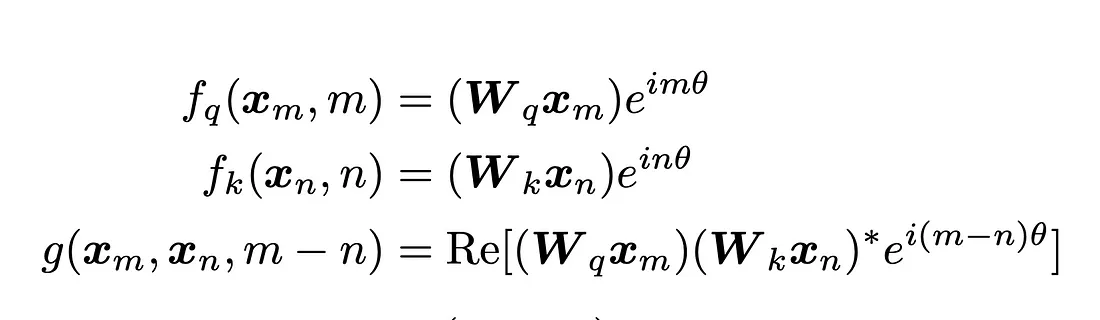
或者图形化地表示为：

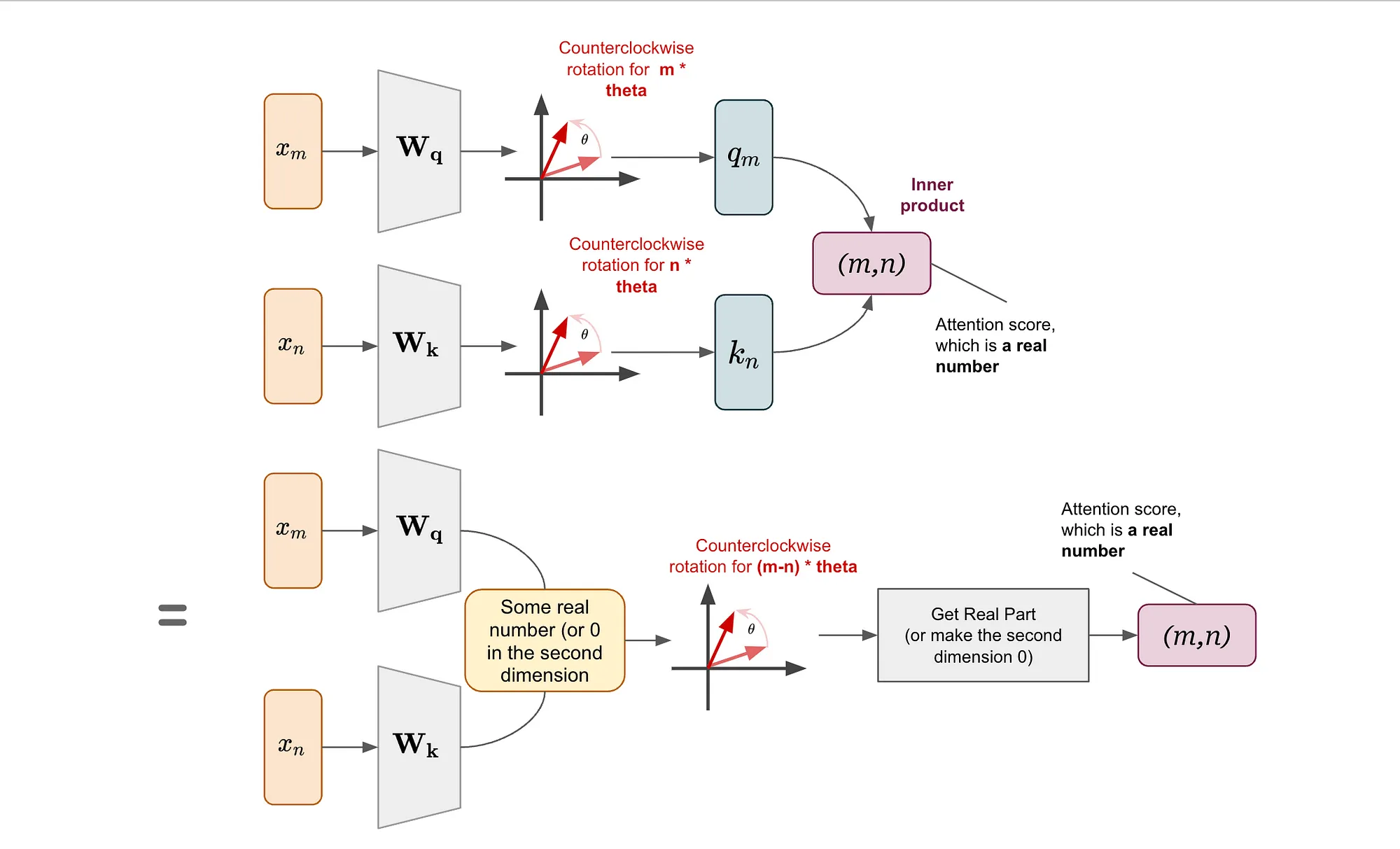
简单来说，这意味着在变换之后，我们可以先旋转再执行内积，或者也可以先执行内积再旋转，然后取实部。在第二种方法中，我们只需要(m-n)来进行旋转，这表明这是一种相对位置嵌入。

这就是旋转位置嵌入（RoPE）背后的直观理解：只需将仿射变换后的词嵌入向量按与其位置索引成比例的角度进行旋转。

RoPE的一般形式

为了将其推广到d维情况，让我们考虑旋转矩阵会是什么样子。作者假设d是一个偶数，因此将d分成d/2个块。每个块分别执行一个2D旋转：

为了将其推广到d维情况，我们需要考虑旋转矩阵的构造。作者首先假设d是一个偶数，因此可以将其分成d/2个块。每个块独立地执行一个2D旋转：

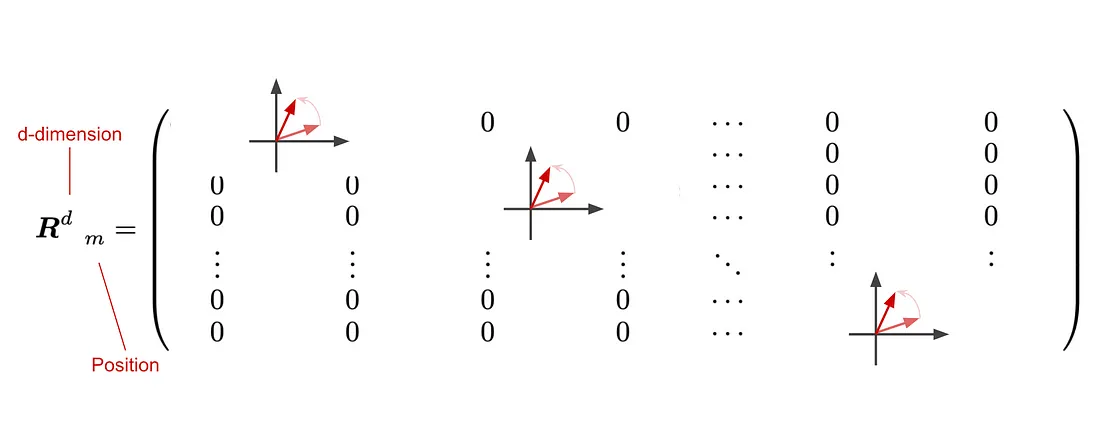
现在的问题是：我们在每个块中旋转多少度？回顾正弦位置嵌入在Transformer中的应用，他们使用的角度参数是：

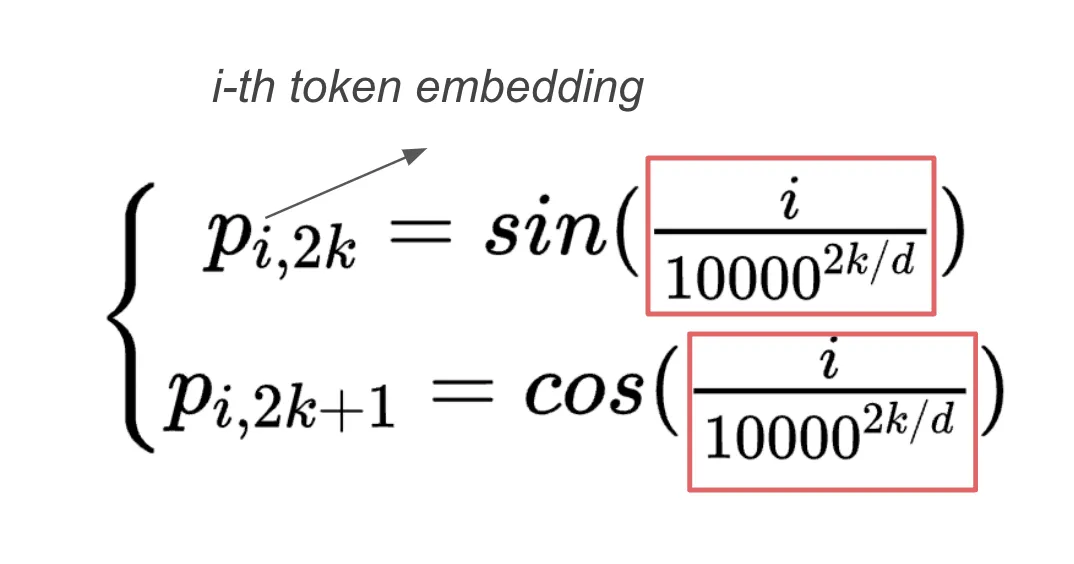
根据这一实现，作者采用了类似的参数：

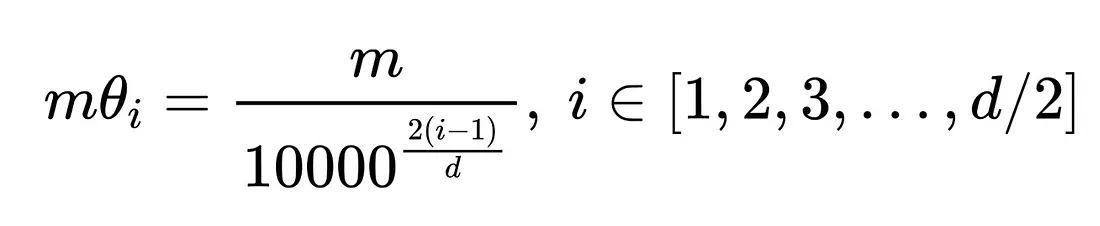
在这里，i表示第i个子块，m·θ决定了对应子块的旋转角度。因此，旋转矩阵的一般形式是：

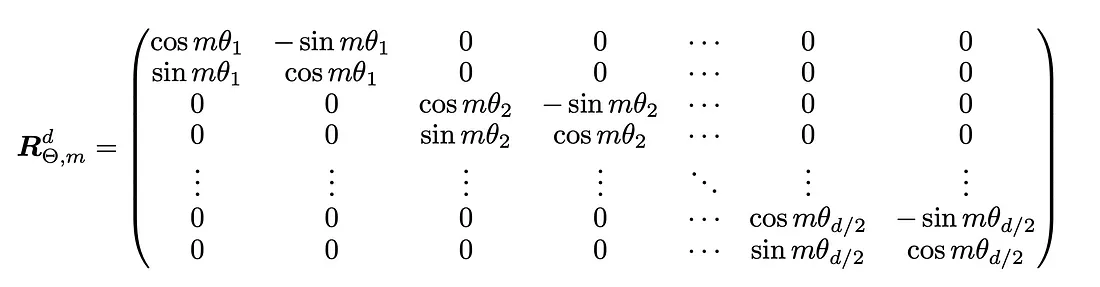
并且应用于标记嵌入的整体变换是：

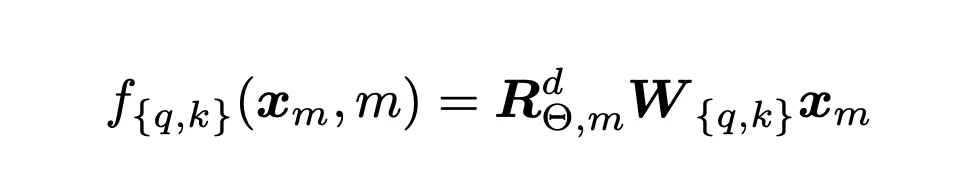
其中，W是查询向量或键向量的d维仿射变换矩阵，R是上面提到的旋转矩阵。以下是原文中的图形解释：

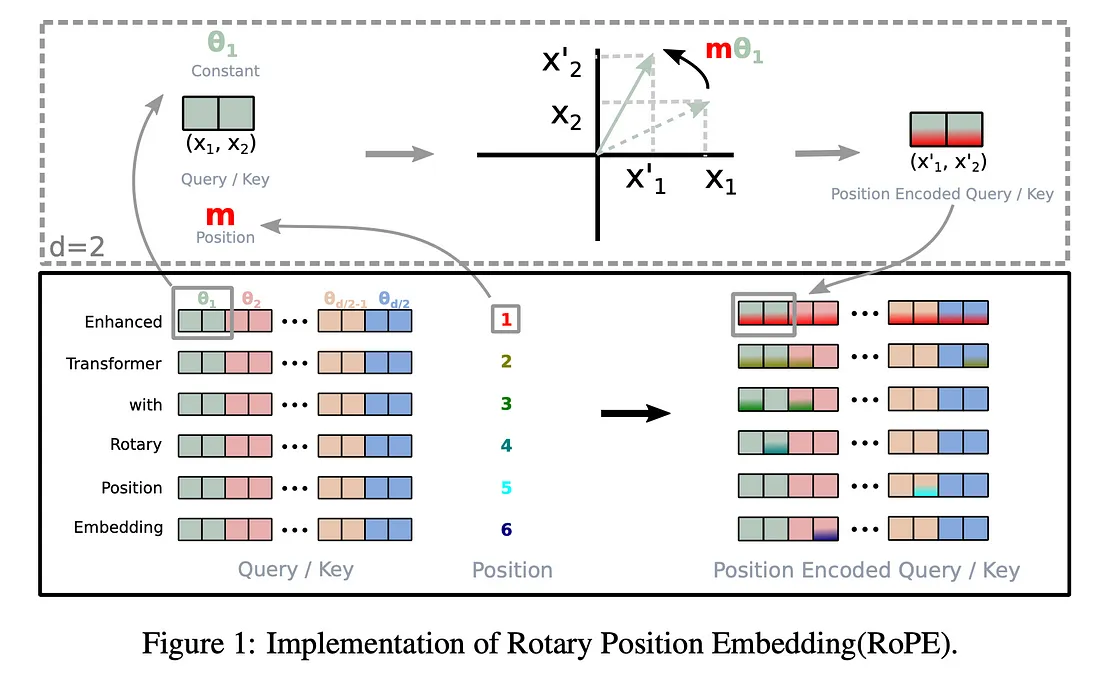
请注意，旋转矩阵R非常稀疏，因此直接乘法运算并不高效。相反，一种计算上更高效的实现R乘法的方法如下所示：

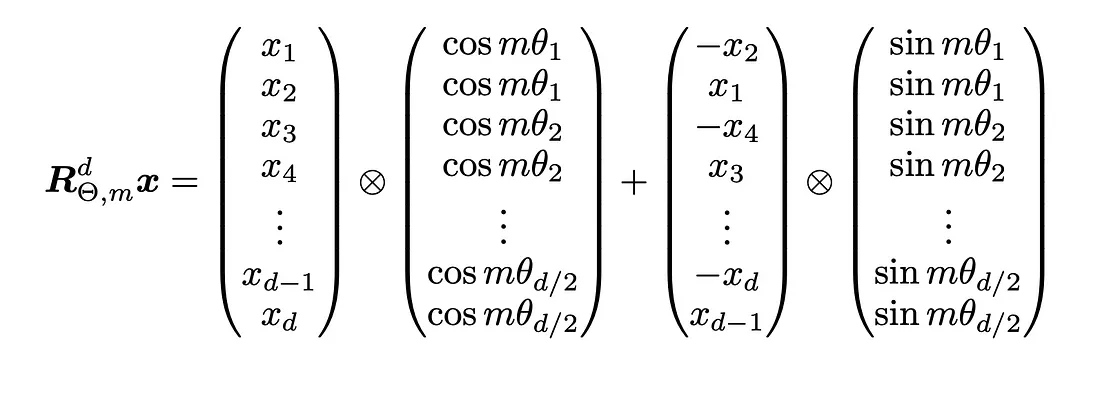
这里的带圆圈和叉号（⊗）的运算符表示逐元素（Hadamard）乘积。

RoPE如何改进语言模型

在原始的RoPE论文中，作者通过在预训练期间用RoPE替换BERT的原始正弦位置编码来验证其性能，由此得到的模型他们称之为ReFormer。在预训练期间，掩码语言建模（MLM）损失表明，使用RoPE的BERT收敛速度更快。

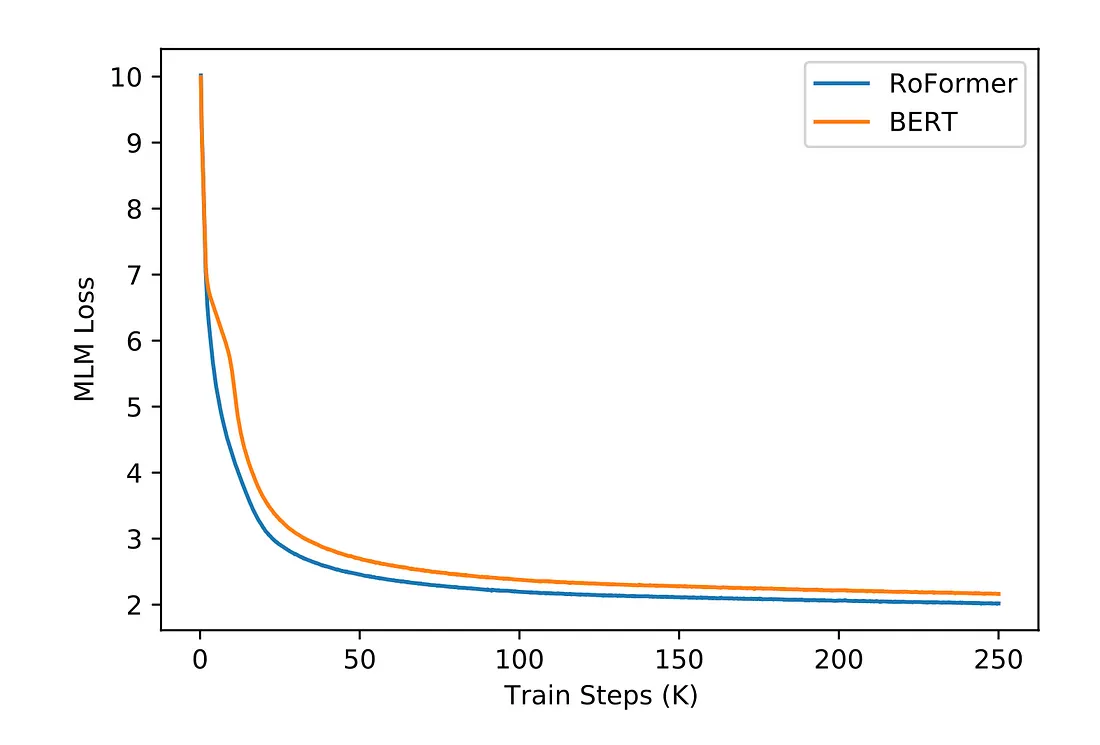
预训练完成后，作者在各种GLUE任务（自然语言处理任务）上对预训练的RoFormer的权重进行了微调，以评估其对于下游自然语言处理任务的能力，结果RoFormer在6个数据集中的3个上表现优于BERT。